起伏地形条件下的低仰角测高方法研究

孟　兵，桂佑林，郭国强

(南京电子技术研究所,　南京 210039)



·总体工程·

起伏地形条件下的低仰角测高方法研究

孟兵，桂佑林，郭国强

(南京电子技术研究所,南京 210039)

针对起伏地形条件下米波雷达低仰角测高问题，提出了一种基于地形扰动建模的低角测高方法。该方法利用垂直放置的天线阵列接收回波信号，基于地形扰动建模，提取起伏条件下的主特征分量，并对目标高度进行一维搜索，通过判定两个信号子空间是否相交来估计得到目标高度。通过计算机仿真和试验分析了方法的测高性能，并验证了该方法的有效性。

低仰角测高；相交子空间；地形起伏；多径

0　引　言

由于具有天生的反隐身优势，米波雷达的研制及其相关技术的发展备受国内关注。低仰角条件下目标高度测量是现代雷达的一个重要任务，也是目前米波雷达技术面临的重要难题之一[1-3]。造成米波雷达低仰角测高困难的主要原因是在低仰角情况下，雷达的波束会照射到地面(或海面)，从而引起电磁波的反射和散射，另外，目标反射的回波也会经地面(或海面)反射进入雷达接收波束主瓣，传统雷达信号处理方法无法有效地消除反射回波，从而影响雷达的低仰角测高性能[4]。在过去的几十年中，人们对该问题进行了大量的研究并提出了许多解决方法。其大体上可以分为以下两类：一类是阵列超分辨技术，如最大似然方法[5]、具有解相干源能力的MUSIC方法[6]以及基于线性预处理的超分辨方法[7]等。这类方法利用超分辨技术将镜像目标和真实目标区分开，以克服多径信号的影响。这类算法测量精度较高，但一般要求信噪较高、运算量较大。另一类是利用多径信号引起的波瓣分裂特性的测高方法，如基于高度分集的低仰角测高方法[8-9]、基于波瓣分裂的低仰角测高方法[10]等。这类方法实现简单、运算量小，但精度不如第一类方法，且对反射地形要求较高。

为了解决起伏地形条件下的低角测高问题，本文提出了一种基于地形扰动模型的稳健测高算法。

1　低空目标回波的多径传播机理

雷达探测和测量低空目标时，雷达天线接收的信号除了直射波外，还有地面或海面的反射波。根据反射面的粗糙程度,反射信号可以分为集中的镜面反射分量和发散的漫反射分量。设反射表面起伏高度为hm，若

(1)

式中：λ为信号波长；α为擦地角。一般可认为反射面是平坦的,其反射信号主要是集中的镜面反射分量,漫反射功率可以忽略。随着hm的增大，即表面粗糙度增大,漫反射的影响越来越大。当表面非常粗糙时，漫反射占主导地位，此时，要用存在多个反射点的漫反射模型来分析多径现象，镜面反射可以忽略。这里假设反射表面比较平坦，主要考虑镜面反射的影响，即雷达接收回波由直射信号和镜面反射信号两部分组成。

根据反射情况的不同，可以将低空目标多径反射分为平面反射和球面反射两种。如果雷达天线传播途径的一端较低，而且反射点非常接近该端，此时可以把地球表面看作为一个平反射面，即平面反射。图1给出了低空目标的经典多径回波平面反射模型。

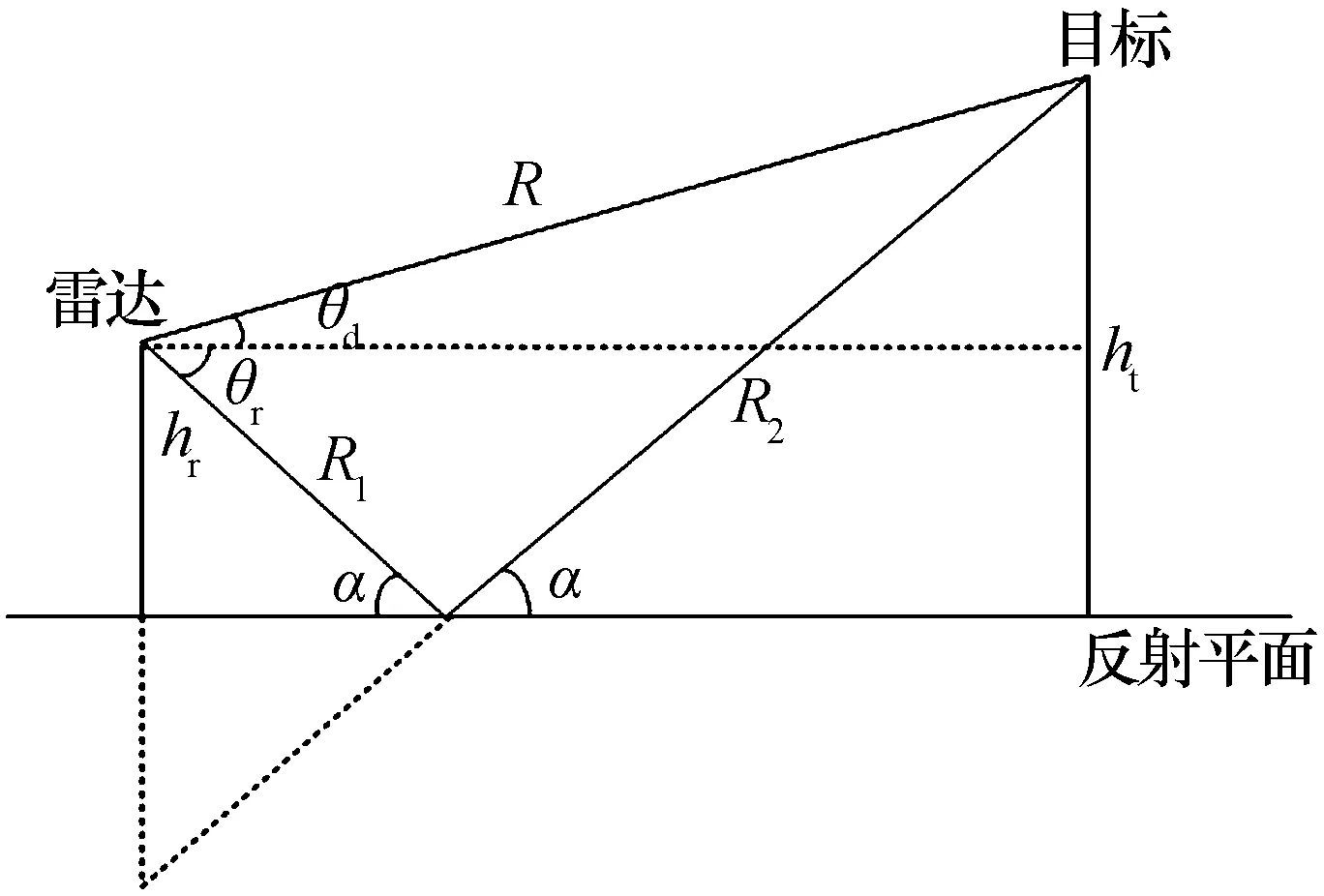
图1　低空目标多径回波的平面模型

假设雷达的高度为hr，目标的高度为ht，雷达距目标的直射距离为R，反射波的距离为R1+R2。根据几何关系，可以求目标及其镜像的仰角分别为

(2)

(3)

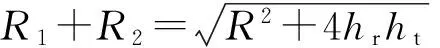
(4)

反射回波和直达回波路径之间的程差为

(5)

如果反射途径低端和反射点较远，地球曲率的影响会变得明显，此时的反射属于球面反射情况。

电磁波经过界面反射时引起能量损失，可以通过反射系数来表征

(6)

式中：|Γ|为Fresnel反射系数，又分垂直极化ΓV和水平极化ΓH两种

(7)

(8)

式中：εc为地面(或者海面)的介电常数，可以查表得到。D为考虑地球曲率的扩散因子，有

(9)

对于大多数地基雷达，一般认为D=1。

因此，天线接收的回波信号可以写成直达回波xd(t)和反射回波xi(t)之和

x(t)=xd(t)+xi(t)=xd(t)(1+ρei(φ-α))

(10)

式中：α为直达回波和反射回波之间的程差引起的相位差；φ为界面反射引起的相位改变。

2　基于相交子空间的低角测高方法

分析了低空目标回波的多径传播机理，给出了多径传播条件下雷达天线接收的回波信号模型，本节将在此基础上分析由多个接收单元组成的天线阵列的接收信号模型，并给出一种基于相交子空间的低仰角测高方法。类似于图1和图2给出了天线阵列接收的目标回波的多径传播模型。

图2　阵列接收的目标回波的多径传播模型

2.1平坦地形条件

接收天线阵列由N个阵元组成，1号阵元距离地面(海面)的高度为h0，阵元间距为d，则阵列各个阵元的高度为：hr(n)=r0+(n-1)d，n=1,2,…,N，接收阵列与目标的水平距离为R，目标的高度为ht。根据图2给出的多径传播模型，可以得到各个阵元与目标之间的直达距离以及它们之间的反射传播距离分别为

(11)

(12)

反射路径和直达路径的路程差为

Δr(n)=ri(n)-rd(n)

(13)

根据式(10)，可以得到第n号阵元的接收信号(经过接收机混频和脉压等处理后)为

sn(m)=x(m)[e-i2πRd(n)/c+ρe-i2πRi(n)/c+w(m)]

(14)

式中：x(m)为信号复包络；c为电磁波在空气中的传播速度，c≈3.0×108m/s；w(m)为接收噪声，这里假定为高斯白噪声，且与目标回波不相关。

将N个阵元接收的信号写成向量的形式为

s(m)=x(m)*(a1+ρeiφa2)+w(m)

(15)

其中，

a1=[e-i2πfRd(1)/c,e-i2πfRd(2)/c,…,e-i2πfRd(N)/c]T

a2=[e-i2πfRt(1)/c,e-i2πfRt(2)/c,…,e-i2πfRt(N)/c]T

对于实际中的低仰角测高问题，距离R以及接收阵高度h0是可知的，那么向量a1和a2仅由目标高度ht决定，则两个向量可以记为a1(h1)和a2(ht)。进一步可以将式(15)写成

s(m)=Ax(m)+w(m)

(16)

其中，A=[a1(ht), a2(ht)]，x(m)=[x(m),ρeiφx(m)]T。则接收回波信号的协方差矩阵为

R=E[x(m)xH(m)]

(17)

对协方差矩阵R进行特征分解，可以得到最大特征值对应的特征向量u1。其中，u1是a1(ht)和a2(ht)的线性组合，可以写为

u1∈span{a1(h),a2(h)}

(18)

假定目标高度为h，根据多径传播模型可以得到直达回波和反射回波构成的子空间，记为

M(h)∈span{a1(h),a2(h)}

(19)

从数学上可以证明[10]，当且仅当h=ht时，信号子空间u1和M(θ)相交。利用这一特性可以来估计目标的俯仰角，具体步骤如下：

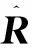
3)假定目标位于某一高度h，计算得到a1(h)和a2(h)，并构造矩阵A(h)；

4)构造矩阵

(20)

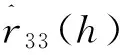
2.2起伏地形条件

起伏模型可以写为

H(r)=H0+ΔH(r)

(21)

式中：ΔH可以根据地形条件，设置相应的统计模型。

不同起伏样本条件下可以建模得到回波集

S=[s(z,H1),s(z,H2),…,s(z,HK)]

(22)

利用建模得到的回波集构造，构造协方差矩阵，并进行特征值分解

(23)

提取主特征分量

A(h)=[u1(h),u2(h),…,uM(h)]

(24)

将式(24)中的A(h)代入式(20)，利用上述步骤，可以实现目标高度测量。

3　仿真和试验验证

将通过仿真实例来验证本文提出的基于相交子空间的雷达低仰角测高方法的有效性，并分析各参数对该方法性能的影响。

仿真条件：20个阵元，阵元间距为2m，频率为50 MHz，接收阵架高为3 m，信噪比为20 dB，通道间幅度起伏0.5 dB，相位起伏5°。

仿真结果：图3和图4分别给出了平坦、起伏(地形起伏方差为3.3 m)条件下常规处理测高算法和稳健测高算法的测高性能。可以看出：1)平坦地形条件下，两种算法性能一致；2)起伏地形条件下，稳健处理算法明显优于常规的处理算法，测角精度改善0.15°(约60%)。

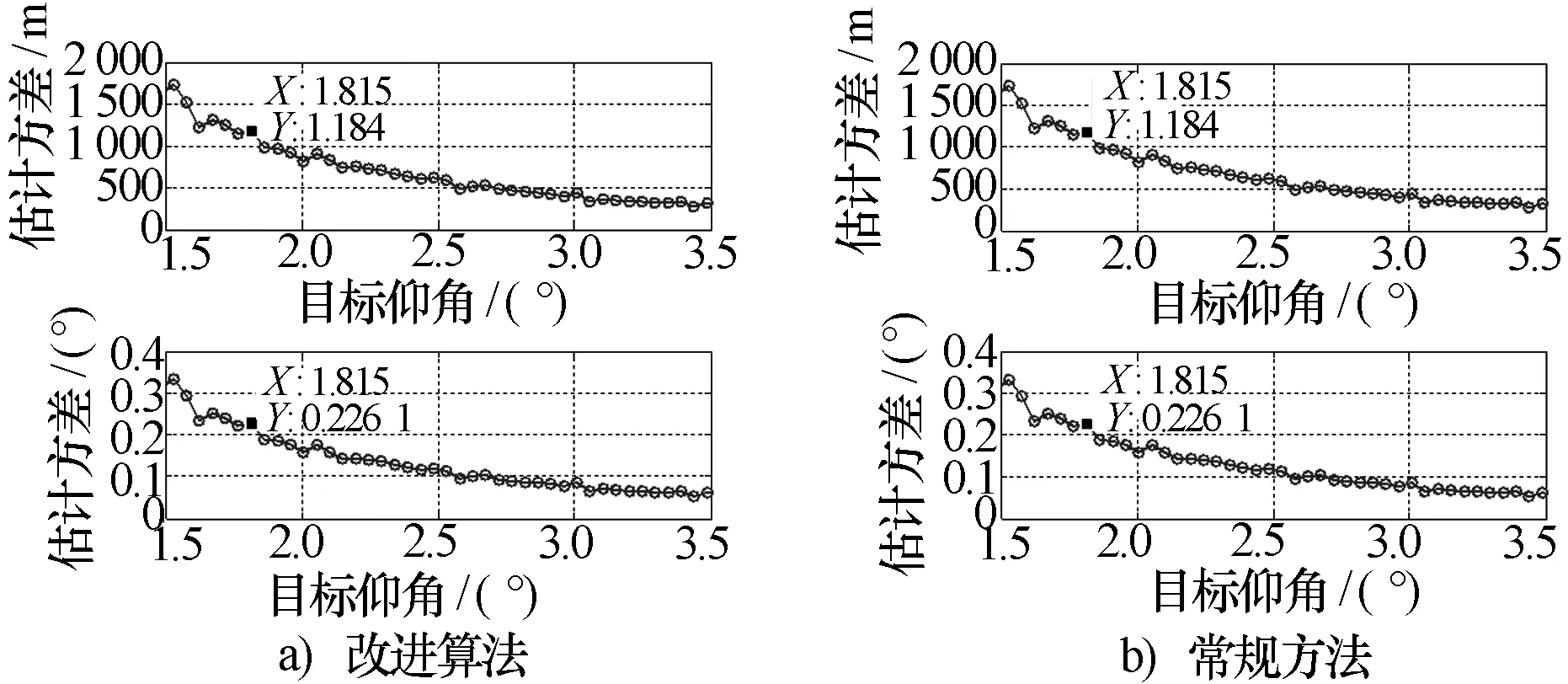
图3　平坦地形条件下两种方法的测高性能

利用某试验平台进行起伏地形条件下测高试验验证，试验场地起伏最大约20 m，试验结果如图5和图6所示。可以看出，试验结果与仿真结论一致。

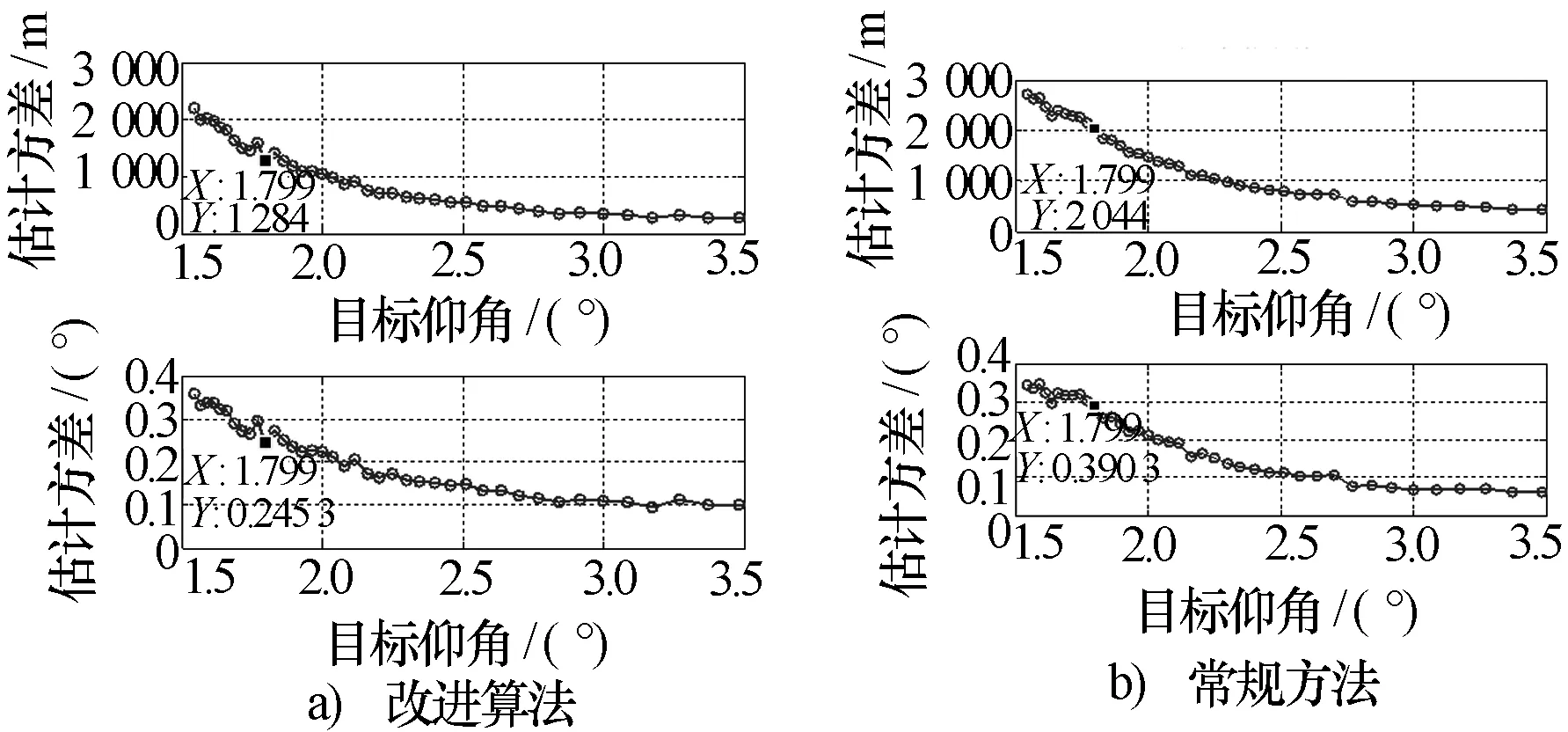
图4　起伏地形下相关法的测高性能

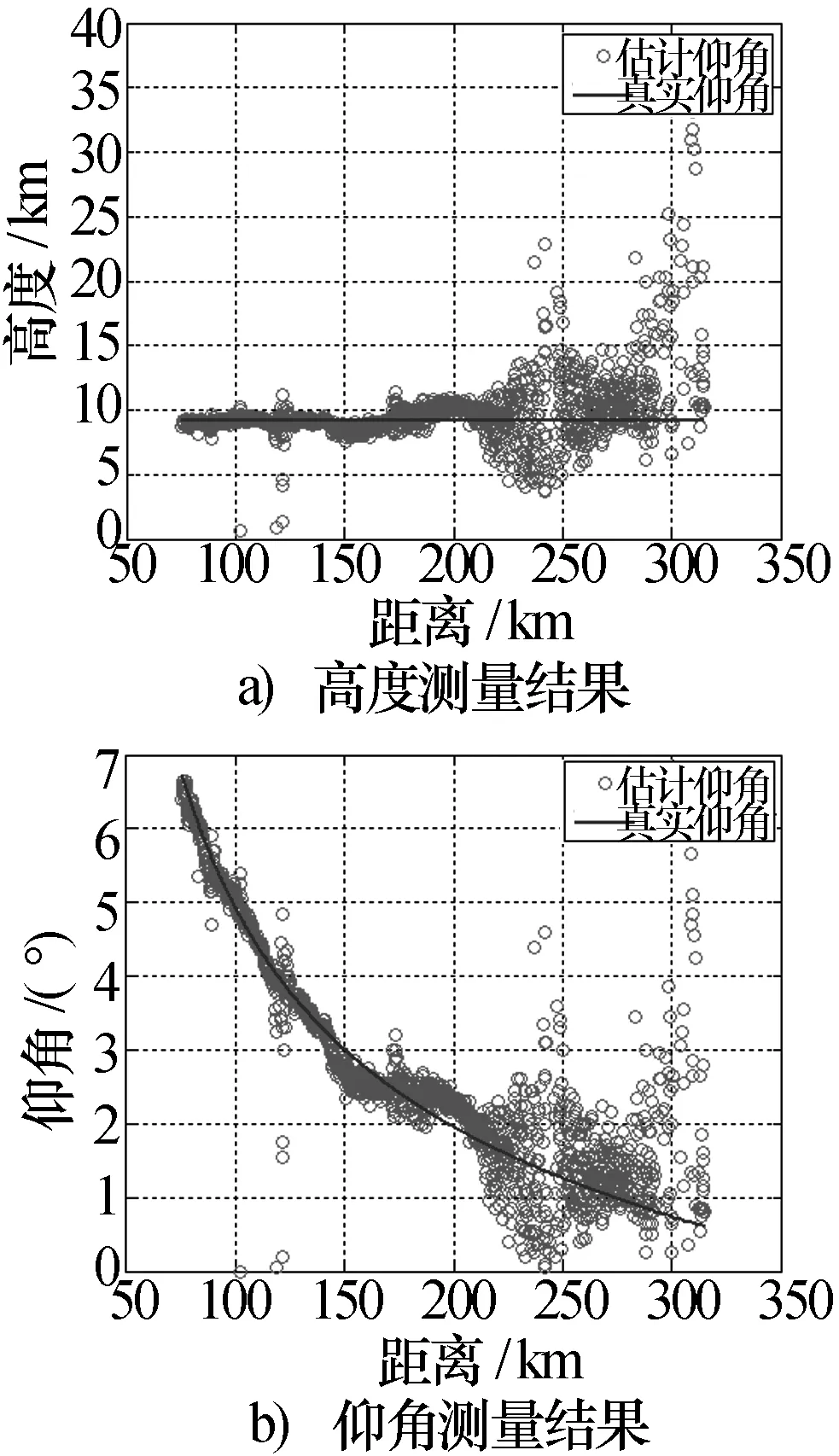
图5　测高试验结果

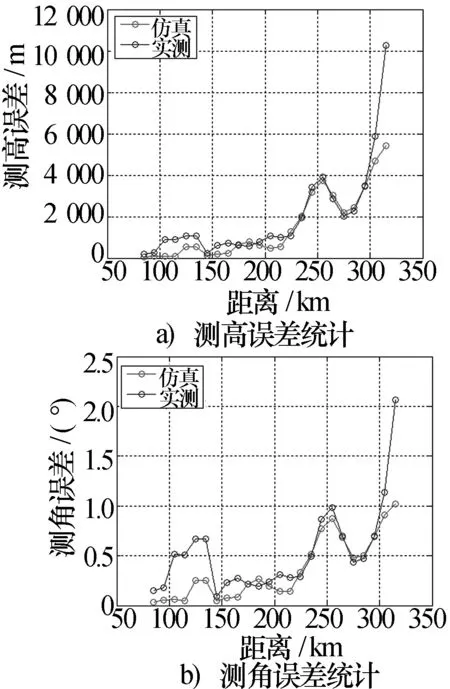
图6　测高仿真和实测精度比较

4　结束语

针对起伏地形条件下米波雷达低仰角测高问题，本文提出了一种基于地形起伏扰动的稳健低仰角测高方法。文中通过理论描述给出了该方法的基本原理，通过计算机仿真和实验分析了该方法的测高性能，验证了该方法的有效性。研究结果表明：基于地形扰动建模，提取主特征分量的方法，可以有效降低地形起伏对测高性能的影响，提高测高算法的稳健性，该算法通过一维搜索实现，具有算法简单、不需要界面反射系数等先验信息、精度高等优点，可以较好地推广应用于实际工程。

[1]WHITE W D. Low angle radar tracking in the presence of multipath[J]. IEEE Transactions on Aerospace and Electronic Systems, 1974, 10(6): 835-852.

[2]TRUMK G V, CANTRELL B H, GORDON W B. Bounds on elevation error estimates f a target in multipath[J]. IEEE Transactions on Aerospace and Electronic Systems, 1979, 15(6): 883-887.

[3]ZOLTOWSKI M, LEE T S. Beamspace ML bearing estimation incorporating low angle geometry[J]. IEEE Transactions on Aerospace and Electronic Systems, 1991, 27 (3): 441-458.

[4]马献德，路彬彬，冯兵. 米波阵列测高的空间平滑算法性能优化[J]. 现代雷达, 2014, 36(10): 49-57.MA Xiande，LU Binbin，FENG Bing. Performance preferences of spatial smoothing algorithm for height-finding method of meter-wave arrays[J]. Modern Radar, 2014, 36(10): 49-57.

[5]赵永波, 张守宏. 雷达低角跟踪环境下的最大似然波达方向估计方法[J]. 电子学报, 2004, 32 (9): 1520-1523.

ZHAO Yongbo, ZHANG Shouhong. Maximum likelihood DOA estimation in radar low angle tracking environment[J]. Acta Electronica Sinica, 2004, 32 (9): 1520-1523.

[6]张文俊, 赵永波, 张守宏. 广义MUSIC 算法在米波雷达测高中的应用及其改进[J]. 电子与信息学报, 2007, 29 (2): 387-390.

ZHANG Wenjun, ZHAO Yongbo, ZHANG Shouhong. Altitude measurement of meter-wave radar using the general MUSIC algorithm and its improvement[J]. Journal of Electronics & Information Technology, 2007, 29(2): 387-390.

[7]吴向东, 张守宏, 董玫. 一种基于线性预处理的米波雷达低仰角处理算法[J]. 电子学报, 2006, 34(9): 1668-1671.

WU Xiangdong, ZHANG Shouhong, DONG Mei. An algorithm based on linear preprocessing for meter wave radars to a target at low altitude[J]. Acta Electronica Sinica, 2006, 34(9): 1668-1671.

[8]苏延川, 赵永波. 基于高度分集的两波束米波雷达测高方法及其应用[J]. 航空计算技术, 2006, 36(6): 58-61.

SU Yanchuan, ZHAO Yongbo. Method and application of altitude measurement based on altitude diversity in two antenna VHF radar[J]. Aeronautical Computing Technique, 2006, 36(6): 58-61.

[9]董玫, 赵永波, 张守宏. 基于高度分集的倾斜阵列米波雷达测高方法[J]. 系统工程与电子技术, 2009, 31(10): 2355-2358.

DONG Mei, ZHAO Yongbo, ZHANG Shouhong. Altitude measurement of VHF radar with oblique array by method of altitude diversity[J]. Systems Engineering and Electronics, 2009, 31(10): 2355-2358.

[10]陈伯孝, 胡铁军, 郑自良, 等. 基于波瓣分裂的米波雷达低仰角测高方法及其应用[J]. 电子学报, 2007,35(6): 1021-1025.

CHEN Boxiao, HU Tiejun, ZHENG Ziliang, et. al. Method of altitude measurement based on beam split in VHF radar and its application[J]. Acta Electronica Sinica, 2007,35(6): 1021-1025.

孟兵男，1976年生，高级工程师。研究方向为雷达侦察信号处理、阵列信号处理、雷达反干扰技术。

Altitude Measurement in Low Elevation Angle Environment with Ground Fluctuating

MENG Bing，GUI Youlin，GUO Guoqiang

(Nanjing Reserach Institute of Electronics Technology,Nanjing 210039, China)

In order to solve the problem of altitude measurement under low angle environment with ground fluctuating, a method of altitude measurement based on ground fluctuant modeling is proposed. In this method, a vertical antenna array is utilized to receive the return signals from targets. Considering the ground fluctuation, we modeled the reflecting path as a statistical processing to extract the primary components. Finally, the real target height is estimated by subspace intersection and one-dimensional height searching. In general, the performance of the proposed method is studied and the efficiency of the proposed method is verified by simulations and experiments under different conditions

altitude measurement in low elevation angle environment; subspace intersection; ground fluctuation; multi-path environment

孟兵Email：meng_nj2000@163.com

2016-03-02

2016-05-20

TN95；TP301.6

A

1004-7859(2016)07-0007-04

DOI：10.16592/ j.cnki.1004-7859.2016.07.002