步进频SAR的波数域成像算法研究
2016-08-29李俊慧汪学刚
李俊慧,王 洪,汪学刚,燕 阳
(电子科技大学 电子工程学院, 成都 611731)
·信号处理·
步进频SAR的波数域成像算法研究
李俊慧,王洪,汪学刚,燕阳
(电子科技大学 电子工程学院,成都 611731)
步进频合成孔径雷达(SAR)可以在不要求系统瞬时大带宽的情况下获得距离向高分辨率,在一些领域已得到了成功的应用,但其成像过程中由于雷达与目标之间存在相对运动使得脉冲间对应的瞬时斜距有不可忽略的差值,基于差值导致的距离像偏移、分辨率下降和信噪比损失,提出了在二维频域中补偿的方法。波数域成像算法主要操作是在二维频域,成像精度较高,计算量适中,文中将该算法应用到步进频SAR中,从雷达的几何关系和信号回波模型出发,推导了补偿斜距差的公式,以及实现残余压缩的Stolt插值过程,给出了目标精确聚焦的完整步骤,并分析了Stolt插值频率改变的过程和参数设计的影响,最后对多个点目标进行了成像仿真。
合成孔径雷达; 步进频信号; 波数域算法; Stolt插值
0 引 言
步进频合成孔径雷达(SAR)是目前国内外高分辨率技术中的研究热点,具有测距精度高、抗杂波能力强、可以识别真假目标和反隐身等优点[1],在军用和民用等领域有着广阔的应用前景。步进频SAR通过合成子脉冲得到的大带宽信号来实现距离向高分辨率[2],通过雷达载机平台的运动,形成长线性阵列来实现方位向高分辨率。平台相对地面静止目标之间的运动分为三种:发射脉冲期间的运动、接收脉冲期间的运动以及相邻发射脉冲之间的运动。步进频SAR的脉冲间运动引起的斜距变化会导致目标距离像的偏移和质量的退化(包括分辨率降低和信噪比损失),必须要补偿这个斜距变化值。
针对补偿方法的研究,文献[3]分析了径向速度对步进频SAR一维距离像的影响 , 也建立步进频SAR的回波模型,但是没有提出具体的补偿方法。文献[4]也研究了雷达与目标之间相对运动对步进频一维成像的影响, 提出一种改变脉冲重复间隔的方法来消除多普勒二次相位,合成距离成像的结果只体现为距离像的平移,而且这一平移量与方位向的脉冲串序号无关,即消除了距离向和方位向的多普勒耦合,避免了距离向分辨率的恶化和信噪比的损失。但这种补偿方法是基于一维成像而言的,对于二维成像不一定适用。由于步进频SAR回波信号的方位向为线性调频信号,可以用驻定相位原理方位向进行快速傅里叶变换(FFT)后变为二维频域信号,其相位中有一项是由脉冲间斜距差引入的,提出了在二维频域中补偿方法。
对于步进频SAR的成像算法的研究,大部分是时域算法。距离多普勒(RD)算法是一种使用广泛的时域成像算法,能同时兼顾成熟、简单、高效和精确等因素。但是该算法存在两点不足:(1)当使用较长的核函数来提高距离徒动校正的精度时,运算量较大;(2)二次压缩对方位频率的依赖性问题较难解决,从而限制了其对某些大斜视角和长孔径步进频SAR的处理精度[5]。后向投影算法(BP)算法也是典型的时域成像算法。文献[6]讨论了使用BP算法对步进频SAR成像,但这种算法的计算量也相对较大。而文献[7]使用步进频脉内调频的信号的SAR的成像方法,与合成宽带方法相似。但是,这种方法对单载频脉冲不适用。
由于本文提出的补偿方法是在二维频域中进行的,所以,后续的成像处理过程是采用频域成像算法。而波数域成像算法的主要聚焦操作是在二维频域上实现的,另外,只要满足速度恒定,就能够在大孔径范围内校正沿距离向的距离徒动变化。同时,步进频SAR一般应用在高分辨率情形下, 波数域算法精度较高,计算量相对适中[8-9],所以本文的步进频成像处理采用波数域算法。
1 步进频SAR成像模型
1.1步进频SAR的发射信号
步进频SAR通过发射多个子脉冲来合成宽带信号,每个子脉冲的频率是不同的,设发射N个子脉冲,n=0,1,…,N-1,第n+1个子脉冲信号可以表示为
st(t,n)=ωn(t)exp(j2πfcnt)
(1)
式中:ωn(t)=rect(t/Tpn)表示矩形窗函数,Tpn表示第n+1个子脉冲宽度;fcn表示第n+1个子脉冲的中心频率。本文设脉冲间步进频间隔Δf是相等的,步进频信号的起始频率为fc,则fcn=fc+nΔf。雷达发射的N个子脉冲的步进频信号波形和频率,如图1所示。
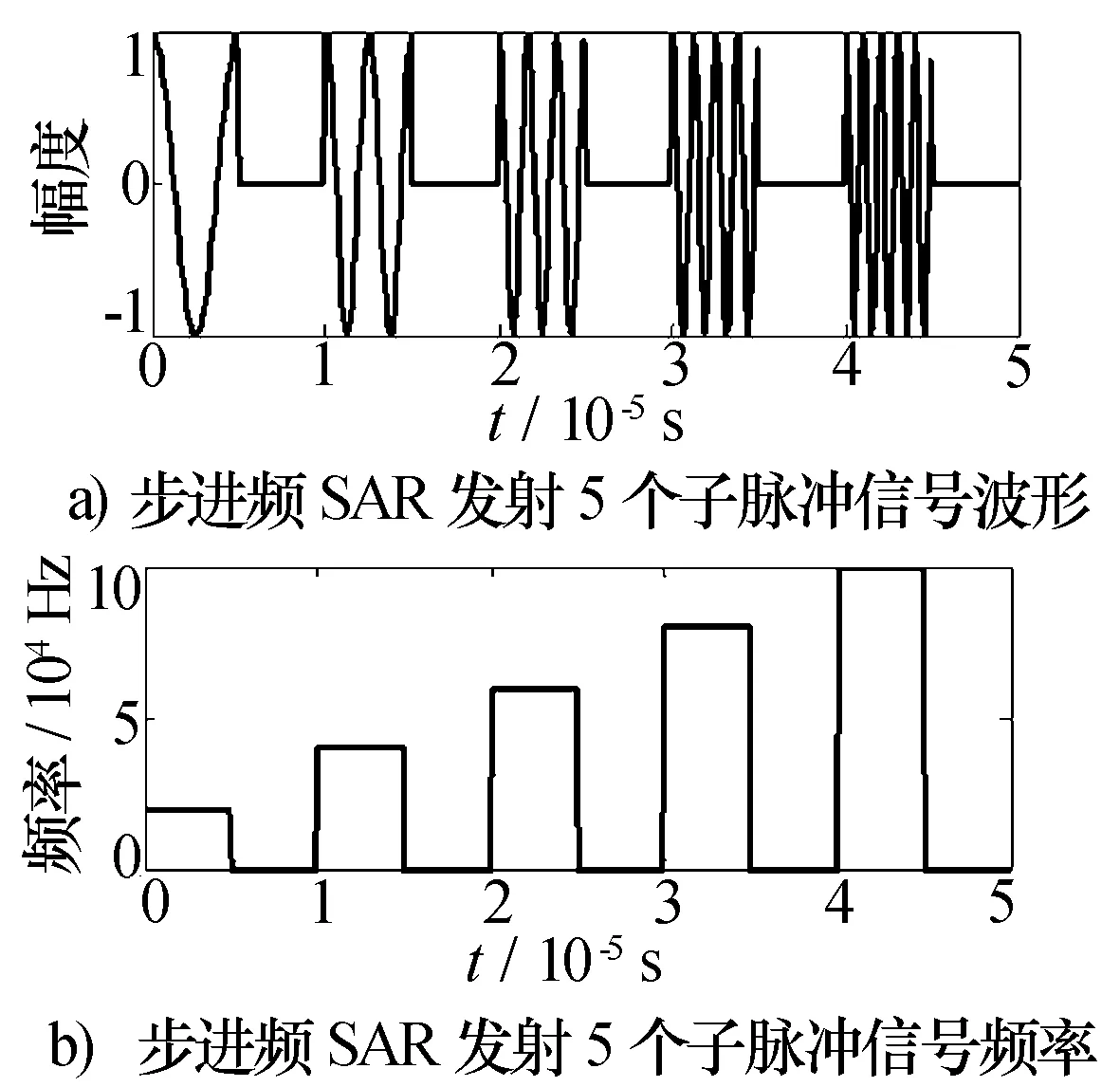
图1 步进频SAR发射信号波形和频率
对于与雷达距离为R的目标,回波时延τ=2R/c,忽略回波信号的幅度,回波信号为
sr(t,n)=ωn(t-τ)exp[j2πfcn(t-τ)]
(2)
对回波信号进行解调,解调后信号为
ωn(t-τ)exp[j2πfcn(t-τ)]·exp(-j2πfcnt)=
ωn(t-τ)exp(-j2πfcnτ)
(3)
将τ=2R/c和fcn=fc+nΔf代入式(3),为
(4)
1.2成像几何关系
为了得到步进频SAR的二维成像[9],需要雷达在方位向上运动来合成孔径。由于雷达的运动,雷达与目标之间的距离R是随着时间变化的,用R(t)表示瞬时距离。设点目标在距离向、方位向二维空间的位置为(0,r0),雷达在方位向运动的速度v,如图2所示,则雷达与目标之间的瞬时斜距R(t)表示为
(5)
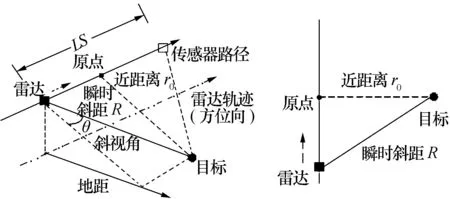
图2 雷达几何关系图
设雷达以重复周期Tr发射子脉冲,在一个合成孔径时间内发射M组步进频脉冲串,每个脉冲串含N个子脉冲。如图3所示,m表示脉冲串序号,n表示子脉冲序号。
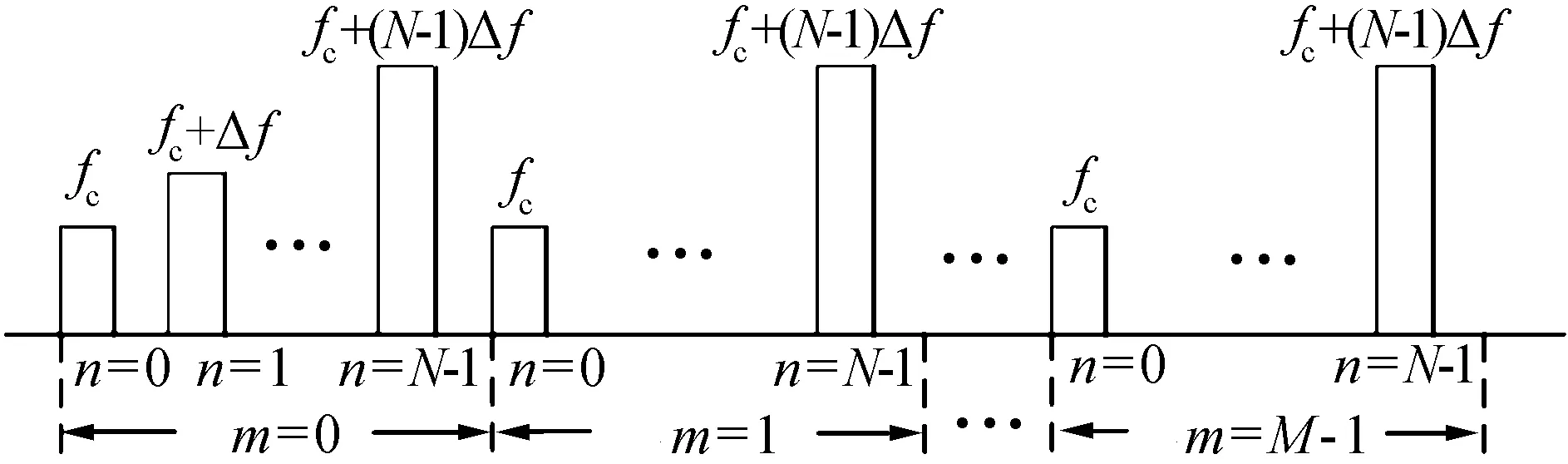
图3 步进频SAR发射多组步进频脉冲串信号
为使得解调后信号可表示为二维矩阵形式, 使得雷达运动时间分成两部分表示,即t=ta+tr,ta为方位慢时间,tr为距离快时间。
步进频信号的脉宽一般比传统的线性调频信号的脉宽小的多,在一个脉冲时间Tr内,雷达与目标之间的距离是近似不变的,即“停-走-停”模式适用。因此,tr=nTr,ta=mNTr。式(5)可以写为
(6)
1.3脉冲间斜距差分析
根据图4所示,对第m+1组脉冲串而言,发射第1个脉冲时,雷达与目标之间的距离为Rm0;发射第n+1个子脉冲时,雷达与目标之间的距离为Rmn。二者之间的关系[10]为
(7)
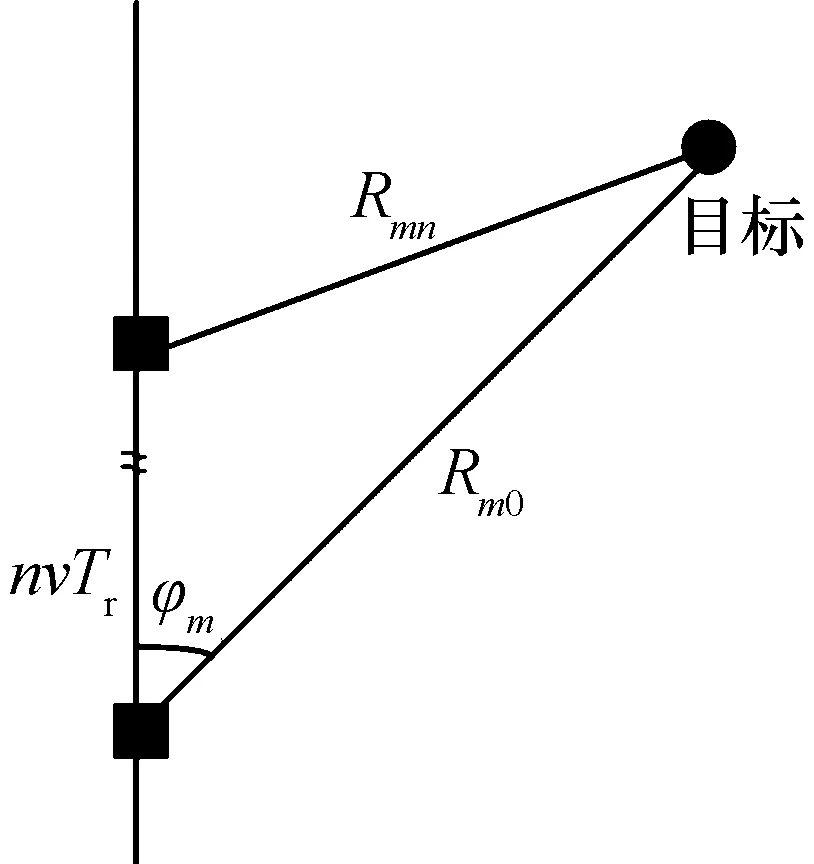
图4 脉冲之间斜距差
一般Rm0≫nvTr,nvTrcosφm/(Rm0-nvTrsinφm)≪1,式(7)近似为
Rmn≈Rm0-nvTrsinφm
(8)
对第m+1组、第n+1个子脉冲的解调后的回波信号采样,提取的一个采样点值为
(9)
第m+1组的N个离散值作IDFT处理,为
(10)
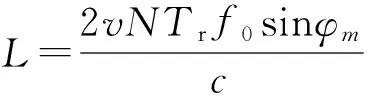
在二维成像处理中,一维距离像的平移、发散和展宽会造成目标回波的非相干叠加,使得最后得到目标成像结果的位置发生偏移和散焦,以及信噪比损失,不利于对目标的检测,必须进行补偿[11-12]。
解调后的回波信号表示为二维形式,为
(11)
将式(6)和fcn=fc+nΔf代入式(11),同时,在ta处,对第n+1个子脉冲回波进行采样得
(12)
2 步进频SAR成像处理过程
本文采用波数域算法对步进频SAR进行成像处理。
令fρn=2fcn/c=2(fc+nΔf)/c=fρc+fρ,x=vta,y0=vTr,R0=r0,式(12)为
(13)
对于步进频SAR,发射一组脉冲串就可以获得距离向信息。根据前面分析,接收的信号经过解调后,每个子脉冲的时间窗函数内任意采样一个点,进行IDFT就可以得到距离向信息,因而信号在距离维可以看作频域。为了获得二维频域信号,只需要对信号在方位向进行傅里叶变换。根据驻定相位原理(POSP)
s(fx,n)=∫s(fx,n)exp(-j2πfxx)dx=
(14)
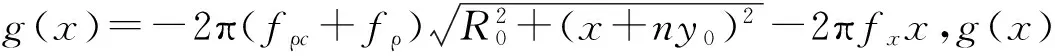
(15)
将式(15)代入g(x)
2πfx(-ny0)
(16)
因而,二维频域信号为
j2πfxny0]
(17)
由于fx=-fρnsinφx,φx=φm,第二项中2πfxny0=-2πfρnnvTrsinφm表示脉冲间斜距误差带来的相位误差,根据1.3节对脉冲间斜距差的分析,脉冲间斜距误差会导致目标的最终成像位置偏移和散焦,需要补偿。补偿函数为
H(fx)=exp(-j2πfxny0)
(18)
补偿后信号为
(19)
波数域算法第一个主要的聚焦步骤是在二维频域实现参考函数相乘(RFM),式(19)信号的相位为
(20)
由于要在二维频域进行参考函数相乘,式(20)的大部分变量都定义在二维频域中。在二维频域中所能使用的最好的相位补偿是将距离R0和雷达等效速度v设在测绘带中心或参考处,此时RFM滤波器的相位为
(21)
该滤波器能够补偿参考距离处Rref的相位,在此处的数据能得到完全的聚焦,经过RFM滤波后,二维频域的残余相位为
(22)
参考函数相乘后,参考距离处的目标得到了良好的聚焦。现需要对其他距离处的目标进行聚焦,可以通过Stolt插值来完成。Stolt插值表示的数值操作,Stolt映射暗示几何变换,后文中交替使用。
Stolt映射改变了二维频域中的数据相位。由于同时调整了距离相位和方位相位,这一插值就消除了式(22)二阶以上的残余相位调制,即Stolt插值完成了残余RCMC和残余方位压缩。由于式(22)中的根式,相位是非线性相位,直接对信号进行距离向傅里叶逆变换,(R0-Rref)≠0非参考距离处目标将会散焦。通过变量代换把根式改成线性相位,即Stolt映射
(23)
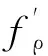
(24)
Stolt插值后,再经过距离向和方位向傅里叶逆变换,目标会得到精确聚焦。
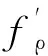
(25)
式中:fρc=2fc/c是初始载波频率;fρ=2nΔf/c是距离步进频率;fx是方位频率,fx=-fρnsinφx=-(fρc+fρ)sinφx。
可以看出,不同的参数设计对Stolt映射的影响主要是在两个方面,一是频率fx和fρ的值;二是方位带宽和起始载波频率,下面具体分析。
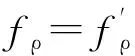
fx=-(fρc+fρ)sinφmax
(26)
将式(26)代入式(25),得到
(27)
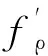
(28)
可以看出,对于固定的最大视线角,fρ取最大值,插值偏移程度最大
(29)
(2)Stolt映射是一个频率偏移的过程,Stolt插值偏移的比例
(30)
将式(29)代入式(30),得到
(31)
可以看出,初始载频与距离带宽比K1=fρc/fρ,max、方位带宽与距离带宽比K2=fx,max/fρ,max对频率偏移有影响,而不是方位带宽和初始载频。方位带宽与距离带宽比增加,初始载频与距离带宽比降低,频率偏移变大,如图5所示。
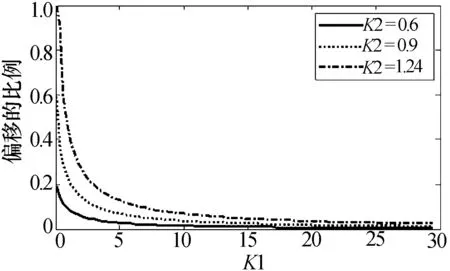
图5 不同的K1和K2对应的频率偏移
步进频SAR成像流程如图6所示,步骤总结:
(1)方位向傅里叶变换将步进频信号变换到多普勒域;
(2)斜距差补偿函数相乘,在二维频域补偿脉冲间的斜距差;
(3)参考函数相乘,是步进频SAR关键的聚焦步骤,参考处目标得到完全聚焦,非参考处目标得到部分聚焦;
(4)Stolt插值,完成非参考处目标的补余聚焦;
(5)距离向逆傅里叶变换完成距离压缩;
(6)方位向逆傅里叶完成方位压缩,将信号变回到时域(即图像域)。
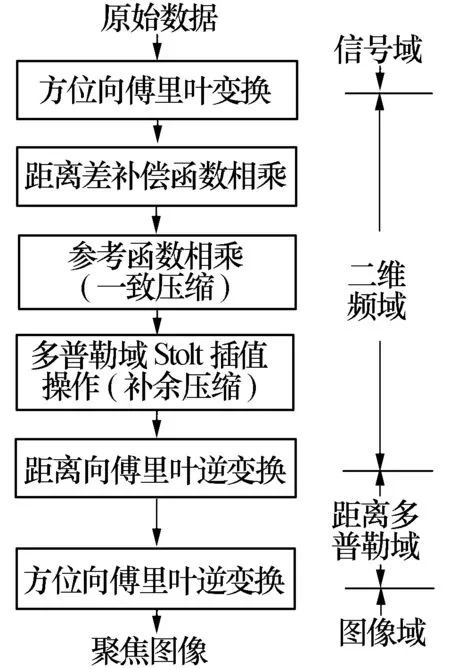
图6 步进频SAR波数域成像算法流程图
3 参数设计及仿真
3.1参数设计分析
步进频SAR信号涉及多个参数,对雷达成像有着较大的影响。
步进频率间隔Δf,决定距离压缩后的最大不模糊距离
(32)
子脉冲宽度Tp,设计时避免混叠,遵循的原则是
(33)
信号带宽B决定距离向分辨率
(34)
子脉冲个数N与步进频率间隔Δf决定信号带宽
B=NΔf
(35)
子脉冲重复时间Tr,成像的最大距离为
(36)
脉冲重复频率PRF为
(37)
避免方位向混叠,则
(38)
式中:v为雷达平台运动速度;θBW为3 dB波束宽度;λmin为雷达的最大波长。
从上述公式可知,为了避免方位向混叠,一方面可以提高PRF,需NTr的值减小。如果是N减小,在距离向分辨率固定时,即带宽不变,Δf会增加,对应的Ru会减小;如果是Tr减小,对应的Rmax会较小。另一方面在θBW固定时,可以增大λmin,则需要雷达选择低的工作频率。因此,设计参数时需要综合考虑。
3.2仿真及结果分析
为了验证上面算法的可行性,进行仿真实验。假设步进频SAR工作在正侧视条带模式下,发射信号的带宽B为500 MHz,频率步进值Δf为1.25 MHz,子脉冲数N为400,脉冲宽度Tp为0.72 μs,脉冲重复间隔Tr为4 μs,场景中心距离Rref为540 m。
对点目标(0 m,545 m)进行仿真分析,图7是补偿了脉冲间斜距差的影响后进行距离压缩成像,可以看出距离徒动是对称的。图8是经过脉冲间斜距补偿、参考函数相乘、Stolt插值后距离压缩成像,校正了距离徒动。为了说明本算法的聚焦能力,仿真了点目标的距离向剖面图和方位向剖面图,如图9、图10所示,图9峰值对应的距离是-0.16 m,图10的峰值对应的距离是545.1 m,3dB带宽对应的距离分辨率为0.3m,方位分辨率为0.485 m,点目标的成像误差没有超过一个分辨单元,距离向和方位向的积分旁瓣比分别是-16.4546dB和-11.491 2 dB。
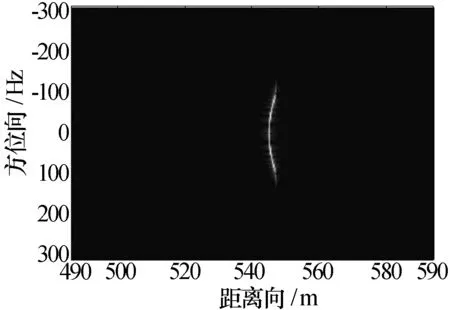
图7 点目标补偿斜距差后距离压缩成像
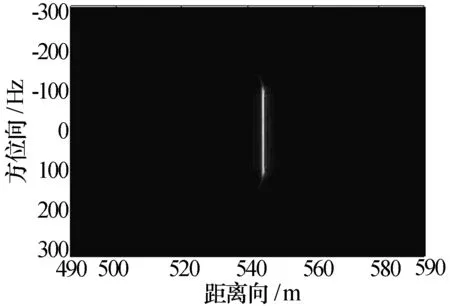
图8 点目标的Stolt插值后的距离压缩成像
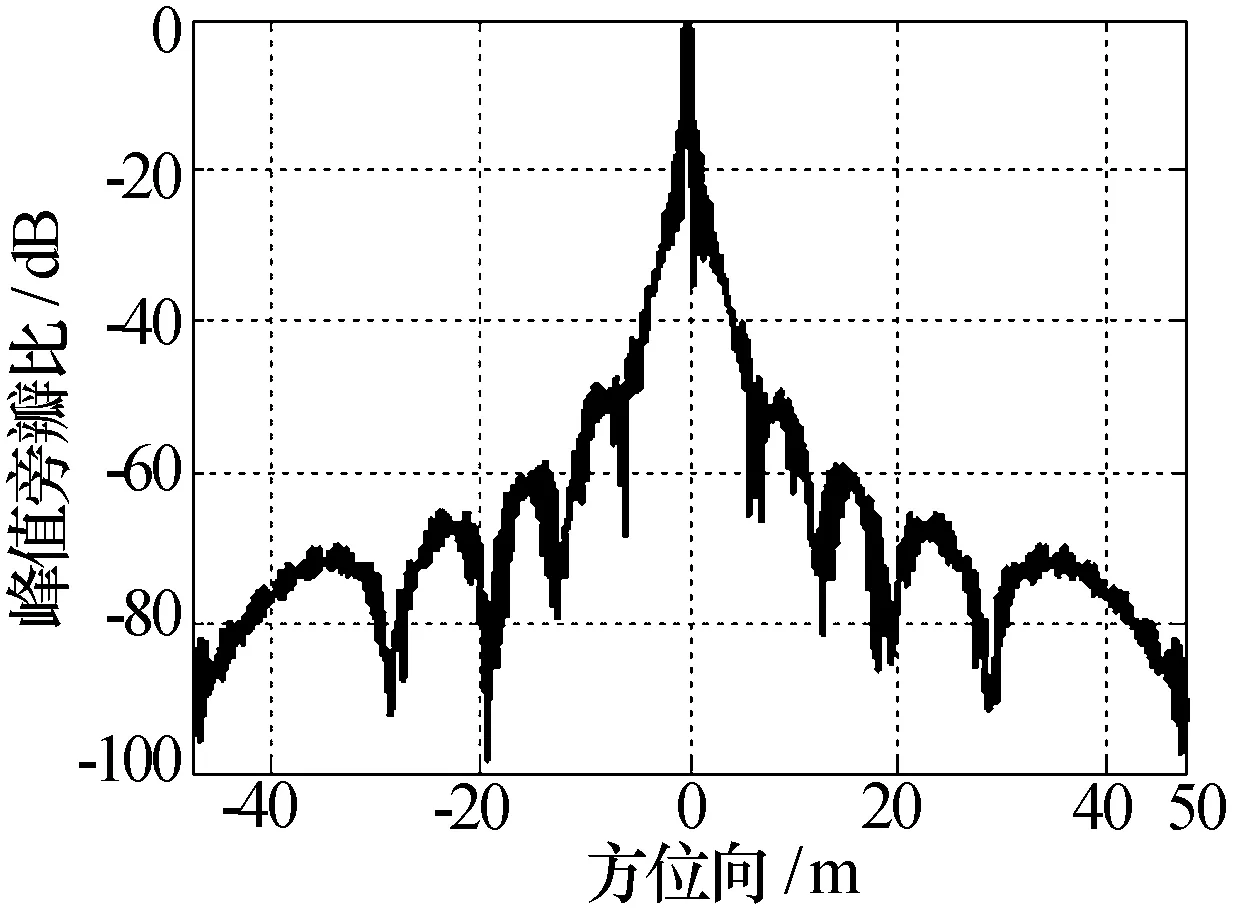
图9 点目标的方位向剖面图
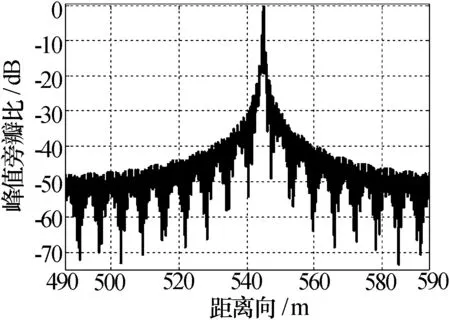
图10 点目标的距离向剖面图
不失一般性,仿真了多个目标(-5 m,535 m)、(5 m,535 m)、(-5 m,545 m)和(5 m,545 m),如图11所示,三维图如图12所示。
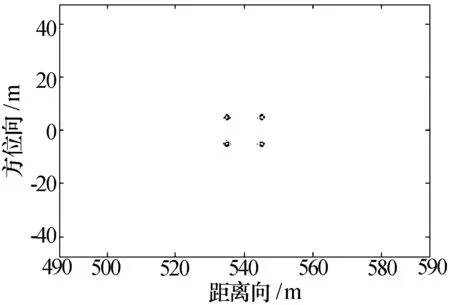
图11 多点目标成像图
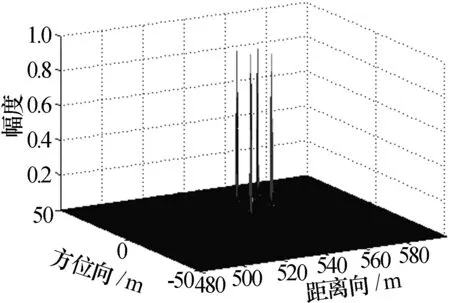
图12 多点目标的三维图
由上面分析可知,仿真的点目标精确聚焦,因而成像算法是有效的。
4 结束语
本文讨论了步进频SAR的成像过程存在的脉冲之间由于目标与雷达存在相对运动而导致的斜距差的问题,提出了在二维频域中补偿的方法。补偿之后,应用了波数域成像算法对步进频SAR进行成像,对算法的具体实现进行了仿真,仿真的结果验证了算法的有效性。
[1]陆必应, 宋千, 王建,等. 步进频率连续波前视探地雷达的研究[J]. 现代雷达, 2010, 32(11): 5-8.
LU Biying, SONG Qian, WANG Jian, et al. A study on a SFCW forward-looking ground penetrating radar[J]. Modern Radar, 2010, 32(11): 5-8.
[2]LEVANON N. Stepped-frequency pulse-train radar signal[J]. IEE Proceedings of Radar, Sonar and Navigation, 2002, 149(6): 297-309.
[3]李海英, 杨汝良. 频率步进信号的合成孔径雷达处理[J]. 电子学报, 2003, 31(3): 349-352.
LI Haiying, YANG Ruliang. Stepped-frequency synthetic aperture radar imaging[J]. Acta Electronica Sinica, 2003, 31(3): 349-352.
[4]安建平, 张润宁, 白克壮. 应用于SAR的一种波形及多普勒效应补偿技术[J]. 系统工程与电子技术, 2000, 22(1): 59-62.
AN Jianping, ZHANG Running, BAI Kezhuang. A novel waveform applied to SAR system and its Doppler phase compensation technique[J]. Systems Engineering and Electronics, 2000, 22(1): 59-62.
[5]张娟. 步进频率雷达高分辨成像处理算法[D]. 西安: 西安电子科技大学, 2011.
ZHANG Juan. High resolution imaging algorithm of a step frequency radar[D]. Xi′an: Xidian Universiity, 2011.
[6]CHEN J, LONG T, ZENG T. A novel high-resolution stepped-frequency SAR signal processing method[C]// International Radar Conference. [S.l.]: IET Press, 2009: 1-4.
[7]HAN B, DING B C, LIANG X D. A new method for stepped-frequency SAR imaging[C]// European Conference on Synthetic Aperture Radar. Germany: IEEE Press, 2006.
[8]保铮, 邢孟道, 王彤. 雷达成像技术[M]. 北京: 电子工业出版社, 2005.
BAO Zheng, XING Mengdao, WANG Tong. Radar imaging technology[M]. Beijing: Publishing House of Electronics Industry, 2005.
[9]CUMMING L G,WONG F H. 合成孔径雷达成像-算法与实现[M]. 北京:电子工业出版社, 2007.
CUMMING L G,WONG F H. Digital processing of synthetic aperture radar data : algorithms and implementation[M]. Beijing: Publishing House of Electronics Industry, 2007.
[10]王鹏宇. 机载步进频率SAR成像方法研究[D]. 长沙: 国防科学技术大学, 2008.
WANG Pengyu. The imaging research of ultra wideband airborne SAR system using stepped frequency waveforms[D]. Changsha: National University of Defense Technology, 2008.
[11]LIU Y, MENG H, LI G, et al. Velocity estimation and range shift compensation for high range resolution profiling in stepped-frequency radar[J]. IEEE Geoscience & Remote Sensing Letters, 2010, 7(4): 791-795.
[12]LUMINATI J E, HALE T B, TEMPLE M A, et al. Doppler aliasing reduction in SAR imagery using stepped-frequency waveforms[J]. IEEE Transactions on Aerospace & Electronic Systems, 2007, 43(1): 163-175.
李俊慧女,1990年生,硕士研究生。研究方向为合成孔径雷达成像处理。
王洪男,1974年生,副教授。研究方向为MIMO雷达、FOD雷达等。
汪学刚男,1962年生,博士生导师。研究方向为雷达信号处理、毫米波雷达系统等。
燕阳男,1990年生,硕士研究生。研究方向为射频通信电路设计、微波器件等。
Stepped Frequency SAR Imaging Using Wavenumber Domain Algorithm
LI Junhui,WANG Hong,WANG Xuegang,YAN Yang
(School of Electronic Engineering,University of Electronic Science and Technology of China,Chengdu 611731, China)
Stepped frequency SAR can obtain the high resolution without the large instantaneous bandwidth, has been successfully used in several areas. Due to relative motion between radar and target there is no negligible instantaneous slant distance difference between pulses. The difference is analyzed in detail, which leads to the decrease of the range profile like offset, resolution and SNR loss. A method of compensation in two-dimensional frequency domain is proposed. The wavenumber domain imaging algorithm mainly operates in two dimensional frequency domain with the higher imaging accuracy and a moderate amount of calculation. So the algorithm is applied to stepped frequency SAR. Starting from the geometric relation and the echo signal model, the formula for compensating the slant distance difference and the Stolt interpolation method to implement residual compression are derived. The complete steps of target's precise focusing are given. The frequency change process of Stolt interpolation and the influence of parameter design of the process are analyzed. Finally, the imaging simulation of multiple point targets is carried out.
synthetic aperture radar; stepped frequency signal; wavenumber domain algorithm; Stolt interpolation
国家自然科学基金资助项目(61139003)
李俊慧Email:1043570861@qq.com
2016-03-16
2016-05-18
TN958.6
A
1004-7859(2016)07-0025-07
DOI:10.16592/ j.cnki.1004-7859.2016.07.007
