焊接顺序对X形坡口环焊结构残余应力的影响

万海波，　王延峰，　李　强，　唐　彬

(1． 上海发电设备成套设计研究院， 上海 200240； 2. 上海电力股份有限公司吴泾热电厂， 上海 200241)



焊接顺序对X形坡口环焊结构残余应力的影响

万海波1，王延峰1，李强1，唐彬2

(1． 上海发电设备成套设计研究院， 上海 200240； 2. 上海电力股份有限公司吴泾热电厂， 上海 200241)

利用有限元软件ABAQUS建立了环焊结构的二维轴对称热力顺序耦合有限元模型，并对模型的准确性进行了验证.利用该模型计算了不同焊接顺序下不锈钢圆筒多道对接焊的残余应力分布.结果表明：不同焊接顺序下的残余应力分布趋势基本一致，轴向应力在焊接接头内壁一侧表现为拉应力，而在外壁一侧表现为压应力；环向应力在整个壁厚方向上均表现为拉应力.就应力值大小而言，焊接顺序对残余轴向应力的影响较大，对环向应力的影响则较小.以最大程度降低焊接结构在服役期间发生应力腐蚀开裂的可能性为依据，确定了最佳焊接顺序.

X形坡口； 焊接顺序； 应力腐蚀开裂； 有限元模拟

大型压力容器环缝对接焊是核电化工等领域常见的焊接结构.由于焊接过程中温度分布不均匀，导致焊接后的构件中不可避免地出现残余应力.残余应力对结构的服役状况产生不利影响，如促进疲劳、应力腐蚀开裂、氢脆的发生[1-2].如果要对焊接构件的完整性进行可靠评价，事先知晓焊接残余应力的分布，特别是焊件厚度方向上的应力分布就显得尤为重要.

工程上，为减小焊接变形，减少焊接缺陷和降低焊接工作难度(清根打磨)，中厚壁容器对接多道焊通常采用对称或非对称的X形(双V形)坡口[3-4].由于存在内、外坡口之分，焊道的先后顺序将变得多样化.此时，控制焊后残余应力应成为选用最佳焊接顺序着重考虑的因素，这是因为许多研究和应用实例表明，在残余拉应力和腐蚀性介质的作用下，压力容器或管道的焊缝热影响区极易出现由内壁向壁厚方向扩展的裂纹[5-7].因此，分析焊接顺序对残余应力的影响，无论是对焊接工艺的优化还是服役状况的完整性评估，都具有一定的实际意义.

鉴于影响焊接残余应力分布的因素非常多，包括接头结构、坡口类型、焊接热输入、焊接层数和道数、焊接顺序以及材料特性等，有限元数值模拟方法已成为国内外评估焊接残余应力分布的最有效手段之一[8-12].顺序耦合热弹塑性有限元法是计算焊接残余应力的主要方法，该方法首先进行传热分析得到焊件的温度场，而后以该温度场作为输入，根据焊件的材料力学性能和边界条件，计算得到应力场和应变场.

笔者利用有限元软件ABAQUS建立一个轴对称二维热弹塑性有限元模型，对带X形坡口的中厚壁圆筒多道对接焊进行模拟，探讨焊接顺序对残余应力的影响，并通过已有的试验数据来验证该模型的准确性.

1　二维轴对称有限元模型

1.1热分析

焊接热过程可认为是熔化后的焊材滴落在坡口里并向周围母材传热的过程，如图1所示.在该过程中，焊材和母材交界线(熔合线)的温度快速上升，在达到材料熔点后保持不变，作为一恒温热源向周围母材传热，传热的时间则通过焊接热影响区的宽度来控制.具体措施如下：预先给出焊接热影响区宽度和临界温度(一般为800～900 ℃)；在热影响区边界上设置温度探测点；传热计算过程中当发现该点的温度达到热影响区临界温度时，立即停止加热，转而进入焊接冷却阶段.焊缝单元将以高于或等于熔点的温度(相当于熔池平均温度)填充至焊件中，随母材一起冷却.以上2D分析方法可获得与实际焊接接头横截面相一致的熔池区和热影响区形状，较好地保证了温度场计算结果的可靠性.

模拟多道焊时，焊缝的依次填充是通过控制相应焊缝单元的“生死”属性来实现的.未轮到填充的焊缝单元预先被赋予“死”的属性，处于未激活状态，不参与模型计算，直至属于它的焊接道次来临而被激活.值得注意的是，焊缝单元的激活伴随有换热边界条件的改变，既存在新换热面的生成，也存在旧换热面的消失,这点在建模时也会考虑到.

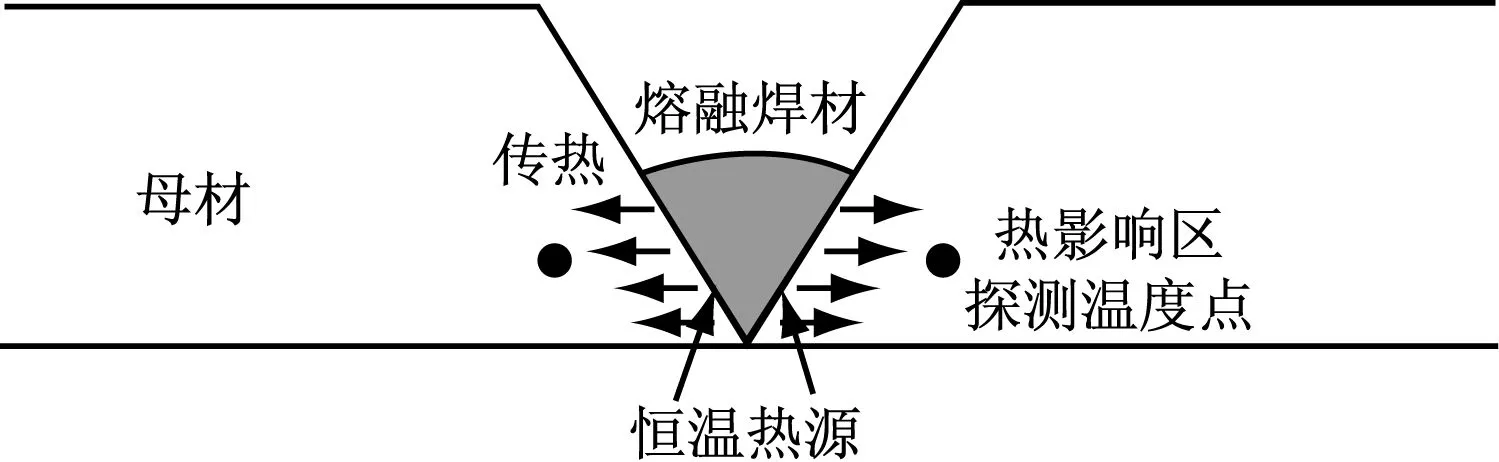
图1　2D焊接热分析示意图

1.2力学分析

力学分析中，每个焊接时间步都将读入热分析得到的温度历史数据，根据预先设定的焊接边界条件和材料热膨胀系数以及弹塑性数据，计算平衡状态的应力和应变.多道焊中，焊缝单元须以无应力的形式填充至焊件中.然而，如果也采用与热分析一样的单元“生死”技术来模拟多道焊，往往会给分析带来很大的困难.主要原因可通过图2来解释.当前一道焊接完成后，整个焊材实际上已经发生了变形，此时激活新焊道单元(注意是从原始位置激活)，其边界节点就必须发生相应的位移以匹配周围的节点,这很有可能使原本形状规则的单元出现较大的畸变，造成计算结果的不收敛.即使计算上能够通过，将未变形填充材料引入变形后的焊件也会导致整个焊件应力的重构，而这并不符合实际情况.

图2　焊接力学分析中单元“生死”技术带来的界面不匹配效应

Fig.2Boundary mismatch caused by element birth technique in multi-pass welding stress analysis

为了解决这些问题，笔者采用Brickstad等人提出的“软化温度”设置法[13]：所有焊道单元在计算过程中都处于激活状态，但是还未被轮到填充的焊缝单元节点将被设定保持在一个较高的温度，称为软化温度.此温度点材料的刚度和屈服强度非常小，可视为处在非激活状态，不会对整个体系的应力计算造成较大的影响，但它们可以随焊件的变形而发生变形.只有在属于它们各自的冷却时间步中，温度处于软化温度下，其材料属性才开始被激活，然后真正参与到整个结构的应力分析中.笔者设置软化温度与材料熔点一致.

1.3几何模型及网格划分

笔者模拟的是带对称X形坡口的大直径圆筒对接多道焊，外径为2 000 mm，壁厚为12 mm，总长为2 000 mm，坡口角度为60°.假定焊道数目为4，内外各2道，共有6类焊接顺序，见图3.顺序1：内道→外道→内道→外道；顺序2：内道→外道→外道→内道；顺序3：内道→内道→外道→外道；顺序4：外道→内道→外道→内道；顺序5：外道→内道→内道→外道；顺序6：外道→外道→内道→内道.

图3　大直径圆筒焊接接头构型及焊道顺序

Fig.3Groove shape and welding sequence for multi-pass butt joints of large-diameter cylinder

考虑到模型关于焊接方向的对称性，仅取一半作为研究对象，如图4所示.采用疏密过渡网格对模型进行网格划分，焊缝附近的温度和应力梯度均较高，因而此处使用较细密的网格，而远离焊缝的位置则使用较稀疏的网格，单元总数为3 094.热分析选用DCAX8R单元，力学分析选用CAX8R单元.

1.4材料性能及参数

所使用的材料为奥氏体不锈钢，并假定焊材和母材具有相同的热物理性能和力学性能.奥氏体不锈钢的热物理性能和力学性能随温度的变化见表1.表中,cp为比定压热容；λ为导热系数；E为弹性模量；ν为泊松比；σy为屈服强度；ET为硬化模量；α为热膨胀系数.Von Mises屈服和双线性随动硬化准则用来描述材料的塑性变形.之所以选用随动硬化模型是因为材料在升温和冷却过程中会有包申格效应的产生[14].模型中使用的参数还包括：熔池平均温度1 500 ℃，层间冷却温度50 ℃，热影响区宽度2.5 mm，临界温度900 ℃.

图4　有限元模型

1.5边界条件

边界条件包括热流边界条件和位移边界条件.热分析中，除对称面外，其他表面均可以通过对流和辐射的形式与外界交换热量.为方便计算，将对流传热系数和辐射传热系数合并成复合传热系数施加在自由面上.不锈钢的复合传热系数可以表达为[13]

(1)

力学分析中，除了在对称面上施加对称性位移边界条件外，还在焊件末端施加了限制刚体位移的边界条件.

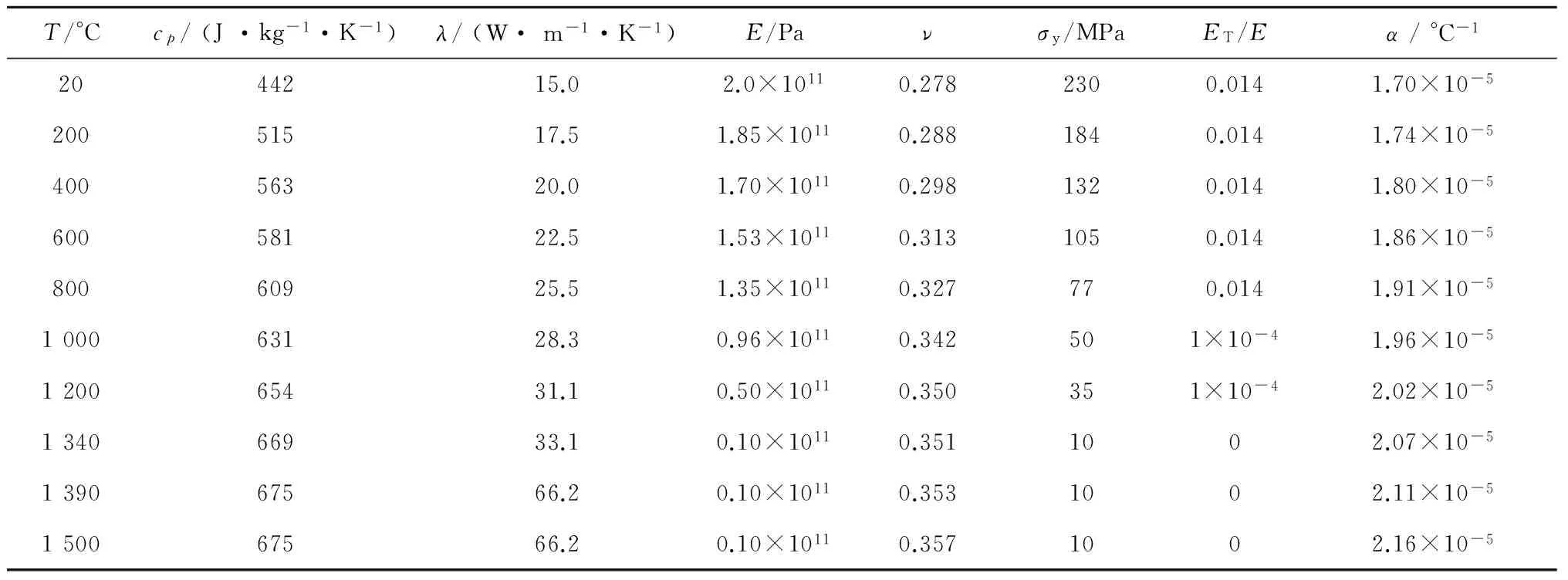
表1　奥氏体不锈钢的热物理性能和力学性能

2　有限元模型的验证

为了验证本模型的可靠性，根据Sattari-Far等人的奥氏体不锈钢管道焊接试验[15](尺寸规格见图5)进行对应的模拟计算，热影响区宽度为2 mm，临界温度为900 ℃.图6为外表面残余应力计算值与试验值(盲孔法试验)的对比图.由图6可知，模拟结果与试验结果吻合得较好，证实了该模型的可靠性.

图5　验证模型中采用的管道尺寸规格

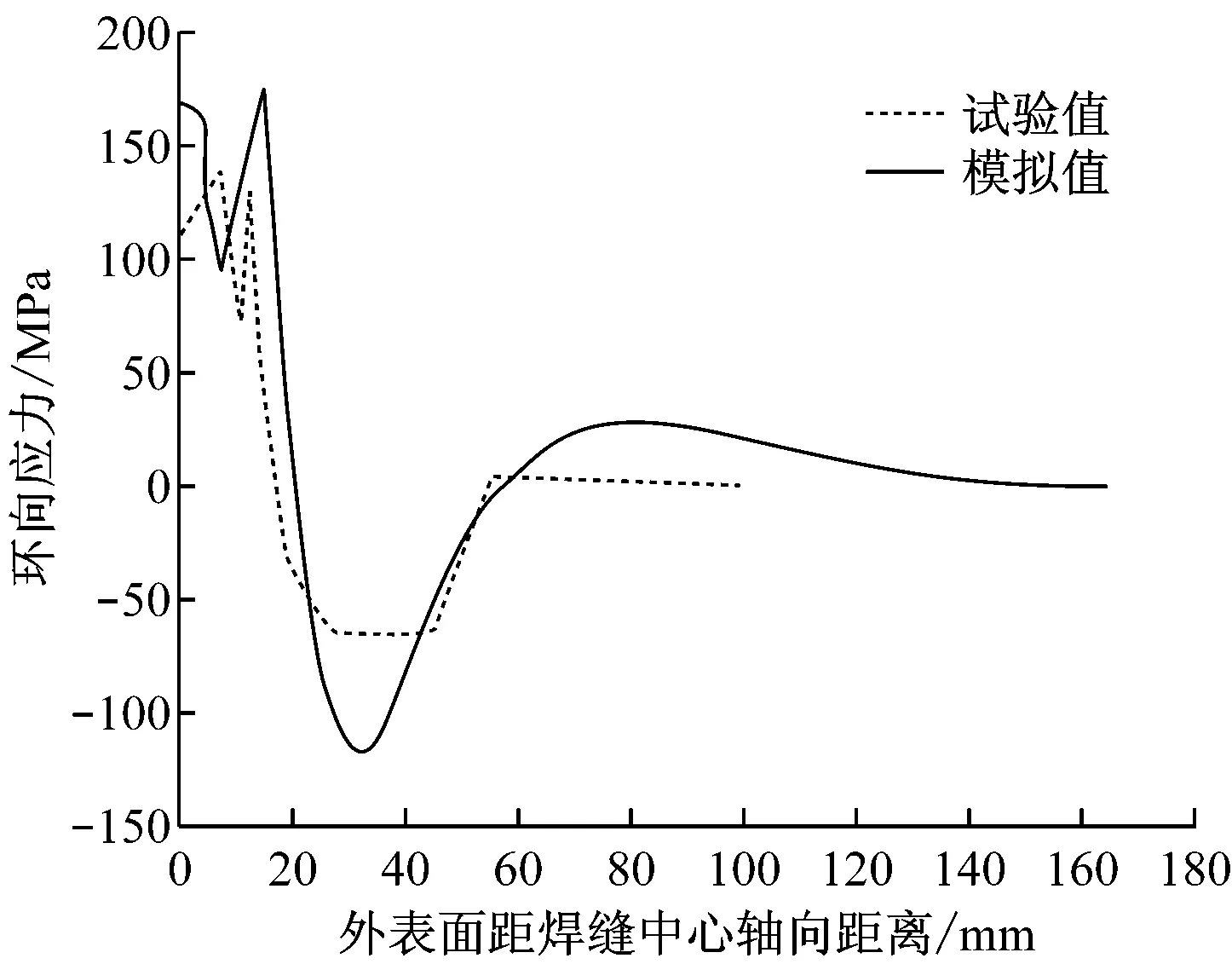
(a) 环向应力

(b) 轴向应力

Fig.6Comparison of outer surface residual stress between FEM results and experiment data

3　有限元计算结果与分析

3.1温度分布

图7为顺序1中各焊道加热阶段的典型温度分布图.温度梯度在焊缝附近非常高，大约2.5 mm的区域内，温度从熔点下降至900 ℃，符合之前设定的热影响区宽度.通过后面的分析可知，该区域实际上将成为整个焊接接头的最薄弱区域.从图7可以看到，未轮到填充的焊缝单元处于不可见的状态，不参与模型计算.随着焊缝单元的添加，模型的自由换热面也将逐步减少.

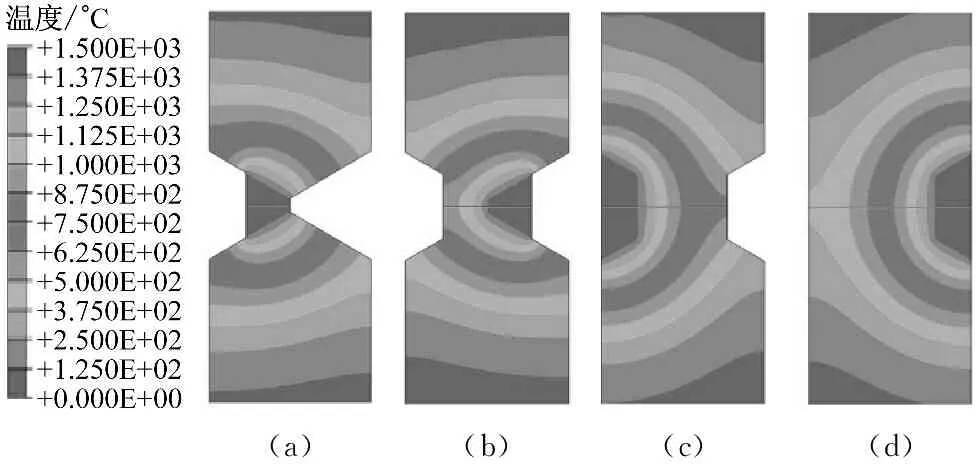
(a)(b)(c)(d)

图7顺序1中各焊道加热阶段的温度分布图

Fig.7Temperature distribution in each pass of weld under No.1 welding sequence

3.2应力分布

图8为顺序1中各焊道加热阶段的典型Mises应力分布图.与热分析不同的是，所有焊缝单元在应力分析中都“显式”地存在，但未轮到填充的焊缝单元由于设定了软化温度，材料刚度非常小，应力几乎为零.正如Brickstad等人指出的一样，这种处理技术保证了未生成单元可以以几乎无应力的形式填充至焊件中.尽管可能会有累积塑性应变的产生，但这对最终残余应力的影响仅存在于非常局部的区域.

(a)(b)(c)(d)

图8顺序1中各焊道加热阶段的Mises应力分布图

Fig.8Mises stress distribution in each pass of weld under No.1 welding sequence

图9和图10分别给出了各焊接顺序下最终残余轴向应力和环向应力沿3条路径的分布情况.3条路径分别如下：(1) 壁厚热影响区边界线(见图3，距熔合线2.5 mm，由内向外)；(2) 内表面轴向方向；(3) 外表面轴向方向.总体来看，6种焊接顺序下的轴向应力和环向应力分布趋势基本一致.轴向应力在焊接接头的内壁一侧表现为拉应力，而在外壁一侧表现为压应力；环向应力在整个壁厚方向上均表现为拉应力，且从内壁向外壁呈现递减趋势.残余应力在焊缝附近非常大，焊缝中心的环向应力甚至超过材料的屈服强度，而在远离焊缝的位置，应力逐渐减小为零.

(a) 沿壁厚热影响区边界线

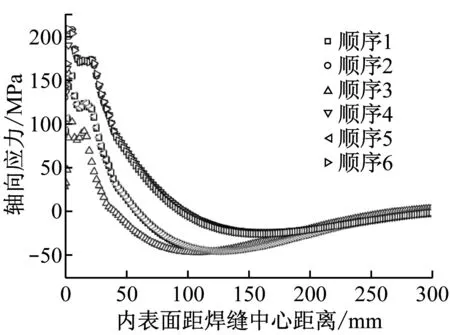
(b) 沿内表面轴向方向

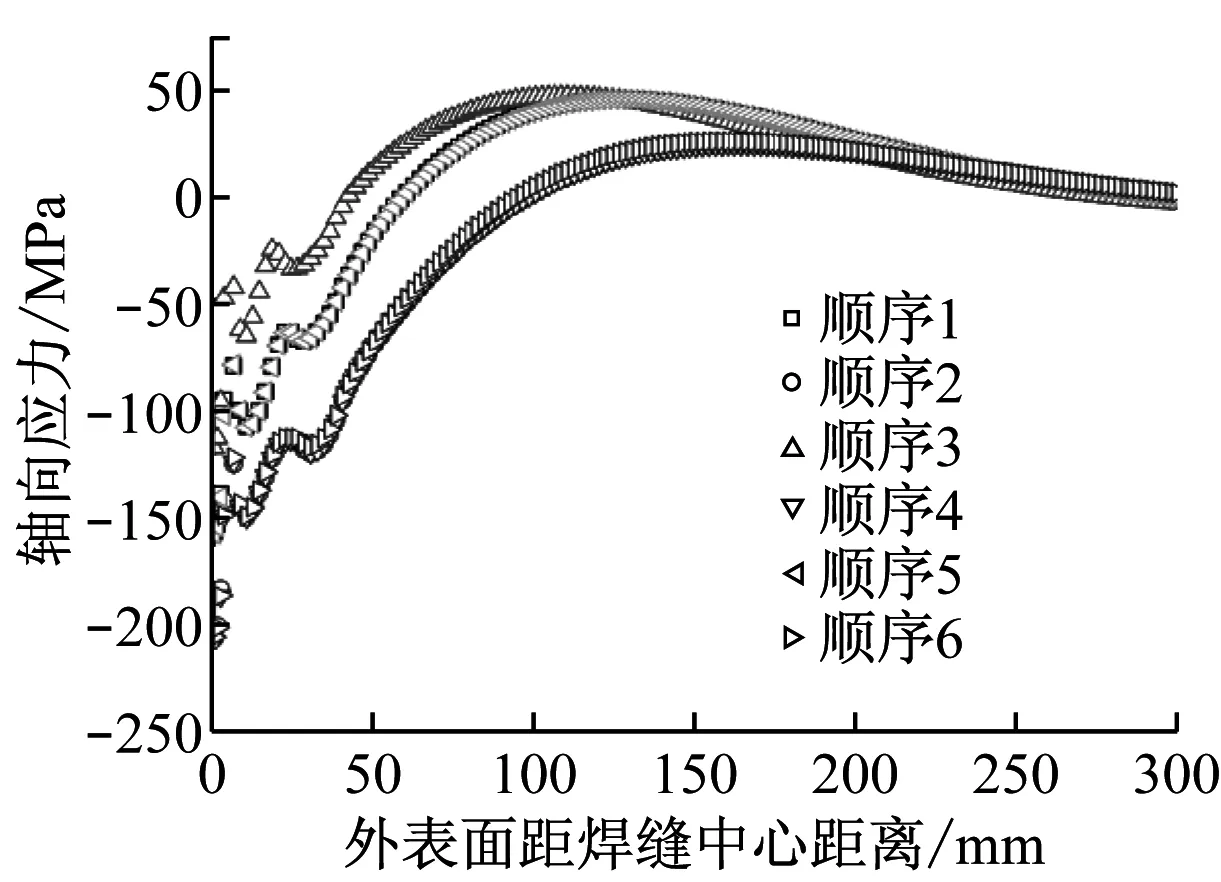
(c) 沿外表面轴向方向

Fig.9Distribution of axial residual stress formed under various welding sequences

6种不同焊接顺序的应力分布实际上表现出了3组不同的结果：顺序2、顺序4和顺序6为一组，顺序1和顺序5为一组，顺序3自成一组.这3组应力的数值大致上呈现出依次递减的趋势.从图2中不难发现，顺序2、顺序4和顺序6的最后一道焊均位于内侧坡口，顺序1和顺序5的最后一道焊均位于外侧坡口，但倒数第2道位于内侧坡口，而顺序3的最后2道焊均位于外侧坡口.这似乎说明最后2道焊的位置对残余应力的影响起着决定性作用.另外，不难看出焊接顺序对轴向应力的影响明显大于对环向应力的影响.3组环向应力仅在中心壁厚外侧区域表现出较大的差异，而轴向应力在整个壁厚方向上均表现出较大的差异.

(a) 沿壁厚热影响区边界线

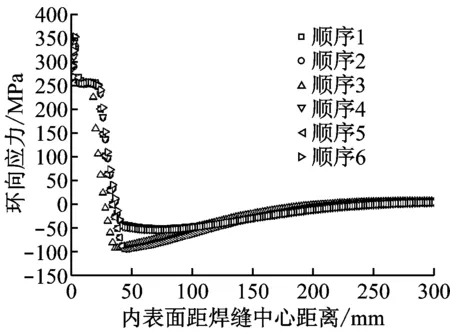
(b) 沿内表面轴向方向

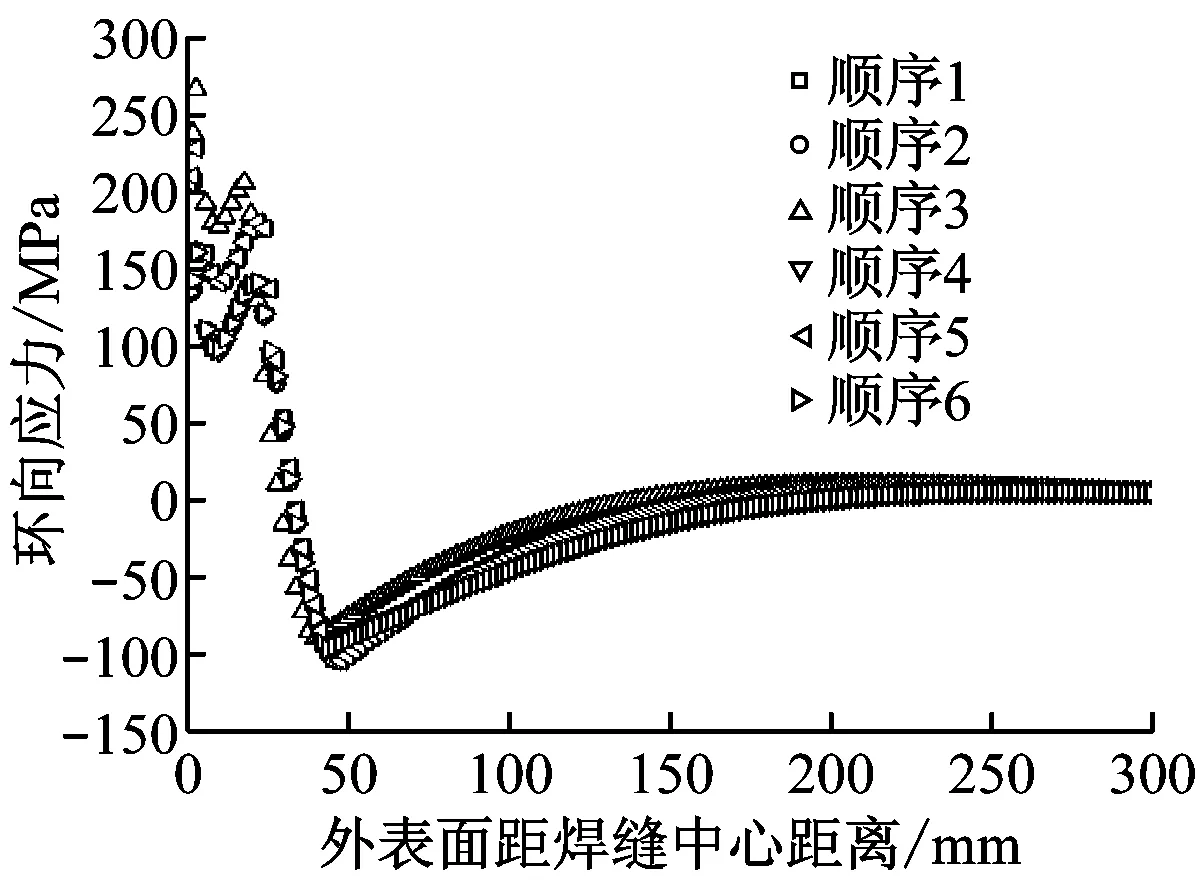
(c) 沿外表面轴向方向

Fig.10Distribution of hoop residual stress formed under various welding sequences

沿壁厚热影响区的轴向应力分布是评估焊接顺序相对优劣的重要指标.众所周知，由于敏化效应，奥氏体不锈钢焊接接头的热影响区是耐晶间腐蚀的最薄弱区域，在拉应力的作用下极易出现应力腐蚀开裂.作为与腐蚀性介质直接接触的表面，内壁热影响区是应力腐蚀裂纹最有可能萌生的地方.减小此处的轴向应力可以阻碍裂纹的形核.即便裂纹在内壁偶然形成，减小沿壁厚方向的轴向应力也可以缓解裂纹的扩展.从这2个角度来讲，顺序3都应被视为最佳焊接顺序.

相比于其他焊接顺序，顺序3的显著特点是末尾两道焊均在外侧坡口.然而这并不能说明对于所有壁厚的环焊结构，将末尾焊道尽可能多地安排在外侧都有助于减小焊缝内壁的残余轴向应力.轴向应力的来源有2个方面：(1) 焊缝轴向收缩；(2) 焊件弯曲变形.轴向收缩效应使得先焊部位对后焊部位产生约束作用，这样后焊部位产生拉应力，先焊部位则产生压应力.与之相反的是，弯曲效应使得后焊部位呈现压应力，先焊部位呈现拉应力.对于壁厚不大且焊道数目不多的管道焊接，轴向收缩效应要大于环向弯曲效应，这时将后期焊道尽量安排在外壁而非内壁一侧将有助于减小焊缝内壁处的轴向拉应力.若壁厚较大且焊道数目多，体系的刚性将增大，因弯曲导致的轴向应力可能大于焊道收缩产生的轴向应力，比如厚板焊接出现的根部硬化和开裂现象[16].在这种情况下，将后期焊道尽量安排在内壁一侧或许会更好.

4　结　论

(1) 基于有限元分析软件ABAQUS建立起环焊结构的二维轴对称热弹塑性有限元模型.在热分析过程中采用单元生死技术模拟多道焊过程，并通过设置温度探测点确定平面传热的时间，以保证获得与试验相一致的焊接热影响区宽度.在力学分析中，使用软化温度技术实现了焊缝单元以无应力形式填充至焊件中，确保了计算的收敛.通过与前人试验的对比，该模型的可靠性得到了验证.

(2) 运用笔者建立的模型，计算了6种焊接顺序下多道X形坡口不锈钢圆筒4焊道对接焊的残余应力分布.不同焊接顺序下的残余应力分布趋势基本一致：轴向应力在焊接接头内壁一侧表现为拉应力，而在外壁一侧表现为压应力；环向应力在整个壁厚方向上均表现为拉应力.就应力值本身而言，焊接顺序对残余轴向应力的影响较大，而对环向应力的影响则较小.

(3) 对于壁厚不大且焊道数目不多的管道焊接，将后期焊道安排在外壁而非内壁一侧将有助于减小焊缝内壁处的残余轴向拉应力，而当壁厚较大且焊道数目较多时，可将后期焊道安排在内壁而非外壁一侧.

[1]KREBS J, KASSNER M. Influence of welding residual stresses on fatigue design of welded joints and components [J]. Welding in the World, 2007, 51(7/8): 54-68.

[2]FUJII C. Factors influencing stress-corrosion cracking of high-strength steel weld metals [J]. Metallurgical and Materials Transactions A, 1981, 12(6):1099-1105.

[3]宣清源, 翁惠娟. 奥氏体不锈钢立罐带钝边X型坡口自动埋弧焊[J]. 压力容器, 1992, 9(5):85-88.

XUAN Qingyuan, WENG Huijuan. Double V groove with root face automatic submerged arc welding for vertical austenitic stainless steel tank [J]. Pressure Vessel Technology, 1992, 9(5):85-88.

[4]付永生, 李颉. 大尺寸立式钢制筒体焊接变形研究[J]. 黑龙江电力, 2012, 34(1):66-67.

FU Yongsheng, LI Jie. Study on welding distortion for large-size vertical steel tank[J]. Heilongjiang Electric Power, 2012, 34(1):66-67.

[5]毛楠. 316L不锈钢焊接接头的组织和力学性能研究[D]. 哈尔滨：哈尔滨工业大学, 2012.

[6]康欢举. 316LN奥氏体不锈钢焊接接头应力腐蚀开裂研究[D]. 上海：上海交通大学, 2012.

[7]杨晔晖, 关凯书. 2205双相不锈钢焊接接头裂纹失效机理分析[J]. 压力容器, 2007, 24(12):26-28.

YANG Yehui, GUAN Kaishu. Failure mechanism analysis on the cracks of 2205 duplex stainless steel weld[J]. Pressure Vessel Technology, 2007, 24(12):26-28.

[8]PENG C, TSO T. Numerical and experimental investigations on the residual stresses of the butt-welded joints [J]. Computational Materials Science, 2004, 29(4):511-522.

[9]MOHR W. Internal surface residual stresses in girth butt-welded steel pipes [C]// Pressure Vessels and Piping Conference 1996.New York,USA: American Society of Mechanical Engineers, 1996.

[10]DENG D, MURAKAWA H. Numerical simulation of temperature field and residual stress in multi-pass welds in stainless steel pipe and comparison with experimental measurements[J]. Computational Materials Science, 2006, 37(3):269-277.

[11]代真，姜运建，章建叶，等. 新型耐热钢焊接温度场与应力场仿真及试验研究[J]. 动力工程学报，2013，33(2): 160-164.

DAI Zhen, JIANG Yunjian, ZHANG Jianye,etal. Simulation and experimental study on welding temperature and residual stress field of new heat-resistant steel [J]. Journal of Chinese Society of Power Engineering, 2013, 33(2): 160-164.

[12]万海波, 李强, 冷晓春, 等. 不锈钢中厚板激光全熔透焊的有限元模拟[J]. 动力工程学报, 2014, 34(2):159-164.

WAN Haibo, LI Qiang, LENG Xiaochun,etal. Numerical simulation for laser full penetration welding of stainless steel plate[J]. Journal of Chinese Society of Power Engineering, 2014, 34(2): 159-164.

[13]BRICKSTAD B, JOSEFSON B. A parametric study of residual stresses in multi-pass butt-welded stainless steel pipes [J]. International Journal of Pressure Vessels and Piping, 1998, 75(1):11-25.

[14]YAGHI A, HYDE T H, BECKER A A,etal. Residual stress simulation in thin and thick-walled stainless steel pipe welds including pipe diameter effects [J]. International Journal of Pressure Vessels and Piping, 2006, 83(11/12):864-874.

[15]SATTARI-FAR I, FARAHANI M. Effect of the weld groove shape and pass number on residual stresses in butt-welded pipes [J]. International Journal of Pressure Vessels and Piping, 2009, 86(11):723-731.

[16]杨明. 厚板焊接残余应力的有限元计算[D]. 北京：北京工业大学, 2003.

Effects of Welding Sequence on Residual Stress Distribution in Circumferential Welded Joints with X-shape Grooves

WANHaibo1,WANGYanfeng1,LIQiang1,TANGBin2

(1.Shanghai Power Equipment Research Institute, Shanghai 200240, China;2. Wujing Thermal Power Plant, Shanghai Electric Power Co., Ltd., Shanghai 200241, China)

Using ABAQUS software, a 2D axisymmetric sequentially coupled thermal-mechanical finite element model was developed for circumferential welds, of which the accuracy was verified with experimental data. The model was then used to calculate the residual stress in multi-pass butt welds of stainless steel cylinder formed under different welding sequences. Results show that the stress distributions formed under different welding sequences reveal essentially the same trend: the axial stress on inner wall side is of the tensile kind and that on outer wall side is of the compressive kind; whereas the hoop stress is of the tensile kind throughout the whole thickness of cylinder wall. As to the stress magnitude, welding sequence affects more on axial stresses than on hoop stresses. An optimum welding sequence is finally determined from the view of preventing stress corrosion cracking in sevice period to the greatest extent.

X-shaped groove; welding sequence; stress corrosion cracking; finite element simulation

2015-08-17

2015-09-09

上海发电设备成套设计研究院青年创新基金资助项目(201408038Q);国家科技重大专项基金资助项目(2015ZX06002004-001)

万海波(1985-)，男，湖南常德人，工程师，工学博士，主要从事电站材料寿命评估和失效分析方面的研究.

电话(Tel．)：18017595079；E-mail：wanhaibo@speri.com.cn.

1674-7607(2016)08-0664-07

TK2

A学科分类号：470.30