高速强湍流风况下的风力机结构动力学响应
2016-08-26缪维跑叶柯华
杨 阳, 李 春,2, 缪维跑, 叶柯华, 叶 舟,2
(1.上海理工大学 能源与动力工程学院,上海 200093;2.上海市动力工程多相流动与传热重点实验室,上海 200093)
高速强湍流风况下的风力机结构动力学响应
杨阳1,李春1,2,缪维跑1,叶柯华1,叶舟1,2
(1.上海理工大学 能源与动力工程学院,上海 200093;2.上海市动力工程多相流动与传热重点实验室,上海 200093)
为研究大型风力机在高速强湍流风况下的结构动力学特性,基于NWTCUP风谱模型建立平均风速为25 m/s的极限湍流三维风场,比例缩放Kelvin-Helmholtz不稳定流的数值模拟结果作为相干结构,将其加入普通湍流风场表示湍流度更强的风况,在FAST软件中分别计算加入相干结构前、后风力机的动力学特性,并仿真偏航30°、紧急顺桨停机和一直顺桨停机3种偏工况,得到各个工况下叶片和塔架载荷的动态响应.结果表明:加入相干结构后,风速在空间及时域的变化均更加剧烈,相干湍动能更大,可表示湍流强度更高的风况;加入相干结构后,风力机动力学响应加剧,其中塔基弯矩影响最大,响应幅值波动变化范围增大了1.96倍;叶片载荷主要刺激频率为风轮旋转频率,塔架响应为塔架一阶侧向振动频率;相干结构对偏工况的影响较大,在偏航和紧急停机等非稳定运行过程中,塔尖弯矩非平稳过程明显.
风力机; 湍流风场; 相干结构; 动力学响应; 偏工况
风力机运行于自然环境下,湍流风的不可控且风速易变等特征直接影响风力机气动弹性响应和结构动力学特性.由于风载荷是陆上风力机的主要载荷,建立合理的随时间及空间位置变化的湍流风场对于有效模拟风力机运行情况具有重要意义.
国内学者大多基于经典风功率谱密度函数建立风场,其中陈严等[1]基于Von Karman速度功率谱密度函数,同时考虑空间节点的相干性,得到不同节点的风速分布.岳一松等[2]和陈晓明[3]假设风速为一组白噪声通过特定滤波器的输出,在此基础上通过自回归模型描述风速的湍流分量,从而建立相应的风速模型,但是没有考虑空间相干性,不能得到相应的三维风场.
国外学者大多通过数学方法预测短时间内的局部风速变化或大时间尺度的区域风场分布情况.Bossanyi[4]通过自回归滑动模型(ARMA)预测了短时间内风速变化.Kariniotakis等[5]比较了ARMA模型和神经网络、模糊逻辑以及小波分析方法在风速预测方面的应用效果,发现应用模糊逻辑预测未来10 min~2 h风速变化的精度相对较高.Nielsen等[6]在ARX模型的基础上加入了气象分析方法,可有效预测未来48 h内风的速度和方向变化.Mohandes等[7]分别通过支持向量机和神经网络算法预测了风速分布.Damousis等[8]通过模糊模型预测了风速分布及相应的功率特性.Bilgili等[9]基于测风塔实测风数据,通过人工神经网络预测风电场年风速分布.上述风速预测方法均可在短时间内获得未来风速分布情况,对于某一节点的风速变化预测结果可靠性较高,但这些方法均需要大量的实测数据支撑,作为近似模型和自回归算法的输入样本,对于三维时变风场的模拟具有一定的局限性.
为建立较为真实的风场作为风力机运行环境,必须考虑风的湍流特征,相干结构(Coherent Structure)是湍流运动的基本特征,Kelvin-Helmholtz不稳定流动是一种典型的相干结构,用于描述自然界连续流场中由于速度梯度而导致涡迅速卷起并破裂的周期性较规则的流动现象.
笔者采用结合了实测风速数据与理论风谱模型的NWTCUP功率谱密度函数,考虑风场计算域的空间相干性,建立三维时变的湍流风场.通过比例缩放Kelvin-Helmholtz不稳定流动的数值模拟结果,并以此作为相干结构加入到普通湍流风况中,实现强湍流风场建模,在美国国家能源部可再生能源实验室(NREL)的开源软件FAST中计算正常运行工况及偏航、紧急停机和停机等偏工况下风力机的结构动力学响应,同时从时域和频域的角度对比分析不同工况下的风力机结构动力学响应动态特性.
1 湍流风场
1.1建立湍流风场
1.1.1风场域划分
与耦合CFD/CSD方法不同,使用FAST软件仿真风力机结构动力学特性时,无需求解整个计算域的流场,风速提前给定,建立风场属于前处理,因此避免了大流域涉及的多尺度问题,较大地提高了计算速度,且比较符合现实情况,是较为准确的研究方法.因此,风场计算域划分只需覆盖整个风轮和塔架.笔者以NREL 5 MW风力机为研究对象,其主要技术参数和结构参数如表1所示.

表1 NREL 5 MW风力机的主要参数
风场计算域以轮毂点为中心,根据所选风力机结构尺寸并考虑塔架可能出现的最大变形量,选择高度和宽度分别为177 m和200 m的风场计算域,如图1所示.风速分量u垂直于风轮平面,分量v和分量w方向如图1所示.高度和宽度分别划分为19和17个网格节点,节点处风速由湍流风谱模型得到,网格节点之间的风速则在计算气动力时通过Hermite插值得到.
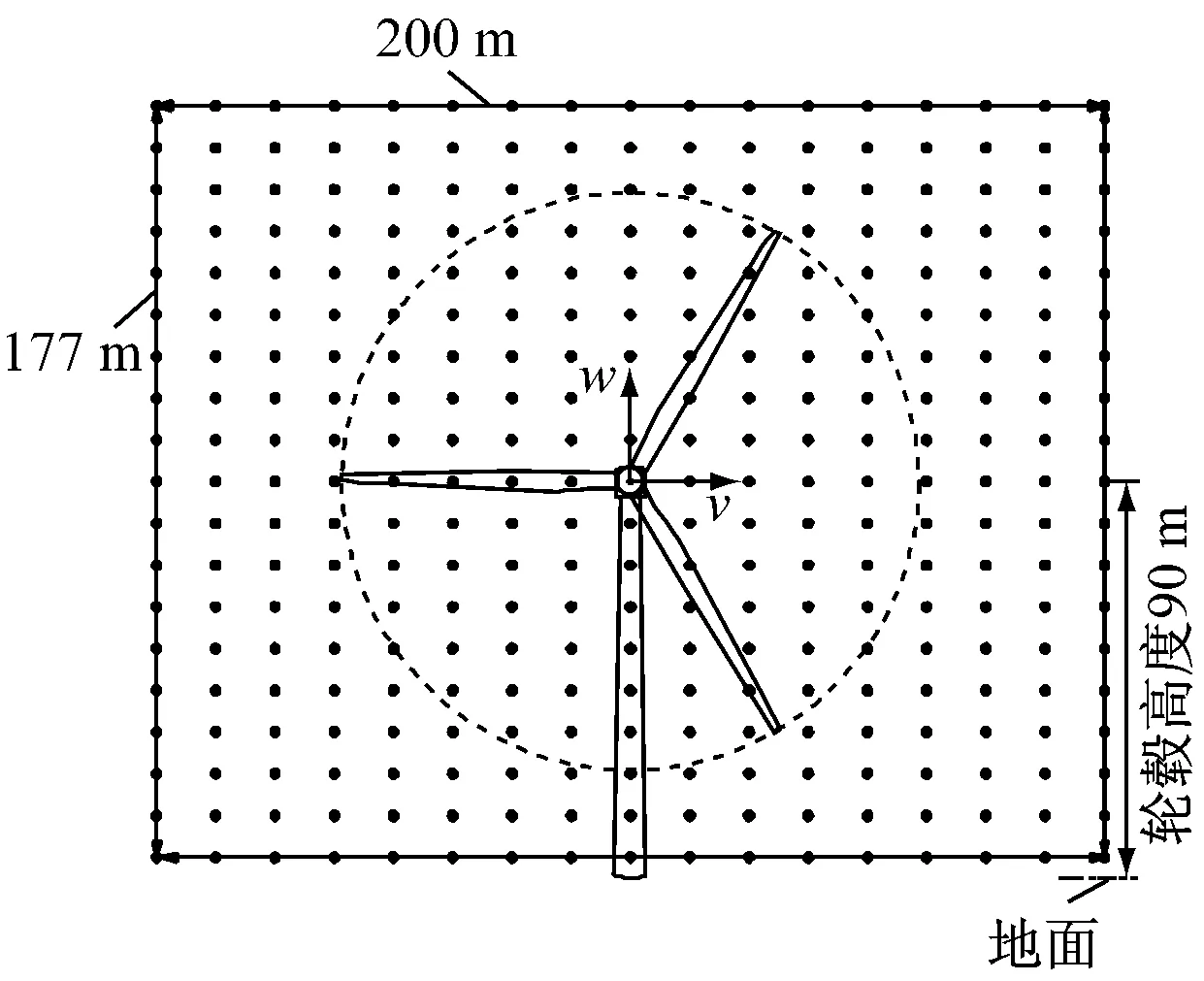
图1 风场域网格划分
1.1.2风谱模型
NWTC/LIST项目[10]是由NWTC和GE Wind 合作,于洛杉矶附近的San Gorgonio风电场开展的一项低海拔风速测量项目,该风电厂地形与中国近海风电场十分类似,能量密度及湍流强度较高.NWTC基于实测风场数据和SMOOTH[11-12]风谱模型建立了NWTCUP风谱模型,通过比例缩放SMOOTH风谱模型功率谱密度函数,具体缩放系数则根据实测数据总结.其中,非稳定流动功率谱通过线性组合高频和低频的SMOOTH风谱得到[13]:

(2)
式中:f为周期频率;K为风向;Pi,K和Fi,K(i=1,2)为缩放系数,由测量数据总结的关于Ri数(Richardson number)的经验函数确定.
高频和低频SMOOTH风谱模型相同,3个方向的功率谱密度分别为:

(3)
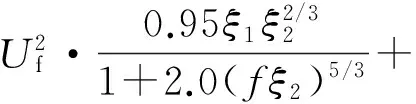
(4)
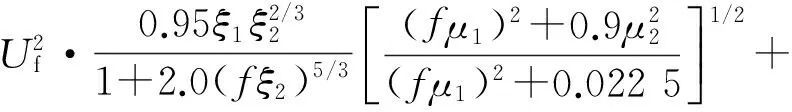
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
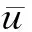
1.1.3空间相干模型和风速廓线
任意给定点的风速和湍流分量可以通过风谱模型得到,但整个风轮扫掠区域的风速分布情况不能通过单一点的风谱表示,水平方向和垂直方向的空间湍流变化关系不能忽略.因此,描述整个风场的风速变化必须考虑节点之间的内在相互关系,这种关系可以通过空间相干模型表示:
(13)
(14)
式中:Si,j(f)为节点i与节点j的互功率谱;Si,i(f)和Sj,j(f)分别为节点i和节点j的功率谱,在同一高度处通常可以认为二者相等[15];C(Δr,f)为空间相干大小;Δr为节点之间的距离;a和b分别为输入的相干衰减系数和相干补偿系数;zm为2个节点的平均高度;η为相干指数,用于定义Solari相干性,本文中取值0.25[16].
NWTCUP风谱模型中b恒为0,a在3个方向的取值为:
(15)
由于大气边界层的存在,空间风速分布呈现明显的近地面风速较低而高空风速较高,即风剪切现象,通过指数分布描述风速垂直方向的变化规律
(16)
式中:Uz为计算节点速度.
1.1.4加入相干结构
通过在普通湍流风上加入相干结构以增强风速湍动,建立强湍流度的高速风场,模拟风力机在此工况下的结构动力学响应.为了量化相干结构的强弱,通过相干湍动能ECTKE定义其大小:
(17)
式中:u′w′、u′v′和v′w′分别为节点处3个平均雷诺应力分量.
相干结构是具有真实时空特征的Kelvin-Helmholtz不稳定流数值模拟结果,首先将其分割成具有无量纲速度信息的固定的无量纲尺寸片段,然后在空间和时间维度进行缩放,以决定对绝对风速的影响[17].通过均匀随机分布规律选择添加的片段,加入相干结构的起始时间为1/4模拟时长,持续时间为1/2模拟时长.
1.2风场模拟结果
以轮毂中心为参考点,其坐标为水平位置0 m,垂直高度90 m.选择该点时程平均风速为25 m/s,仿真时间为600 s,时间步长为0.01 s,逆FFT变换NWTCUP风谱模型并考虑空间相干性,得到各个网格节点处风速.模拟所得普通湍流风场在7个时间步的风速分布如图2所示.由图2可以明显看出,风场域风速分布情况随时间不断变化,且在垂直方向出现明显的风剪切现象,靠近地面处风速较低,随着高度增加风速也不断增大.
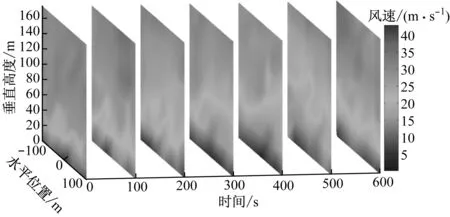
图2 普通湍流风场在7个时间步的风速分布
Fig.2Wind speed distribution of normal turbulence wind field at 7 time steps
在150 ~450 s内,随机地加入相干结构.图3为300 s时加入相干结构前后风速和相干湍动能的比较.由图3可知,加入相干结构后空间风速分布出现2个明显的涡结构,风速大小差异更大,且平均风速增大,风轮旋转区域相干湍动能亦明显增大,说明加入相干结构的有效性.
图4为轮毂点处加入相干结构前后的3个速度分量和相干湍动能的变化.由图4(a)可以发现,加入相干结构后,3个方向的速度分量均出现明显的剧烈波动,尤其是速度相对较低的w和v方向分量,剧烈的变化不仅引起风速绝对大小的波动,更会造成风速方向的突然变化.相干湍动能表示某一时刻速度与时程平均速度的差异大小.由图4(b)可知,加入相干结构后的风场,相干湍动能最大值和平均值分别增大了49%和38%,表明加入相干结构后的风场风速更加不稳定,在一定程度上可以代表风向和速度均剧烈变化的风场.
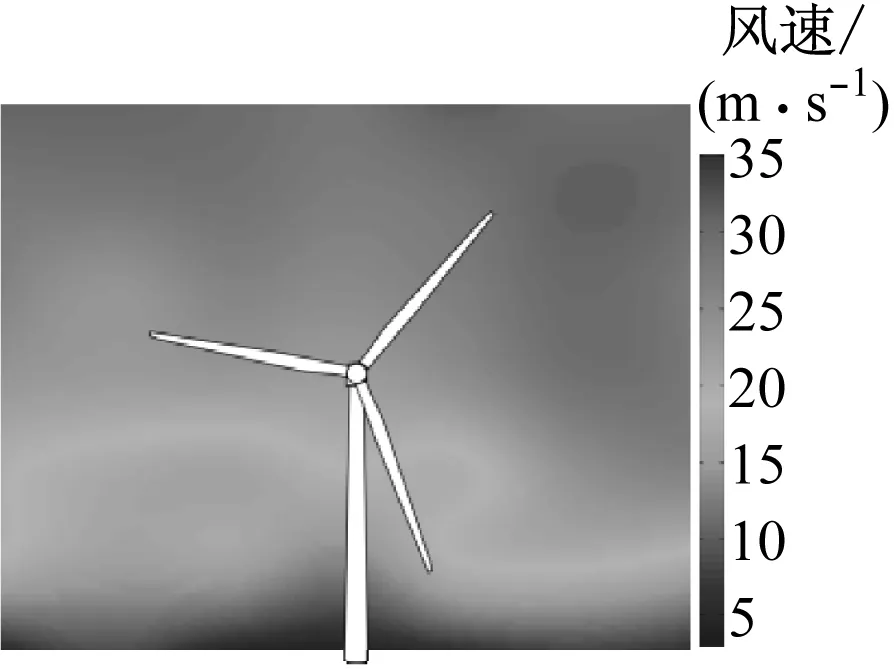
(a)t=300 s风速

(b)t=300 s风速(加入相干结构)
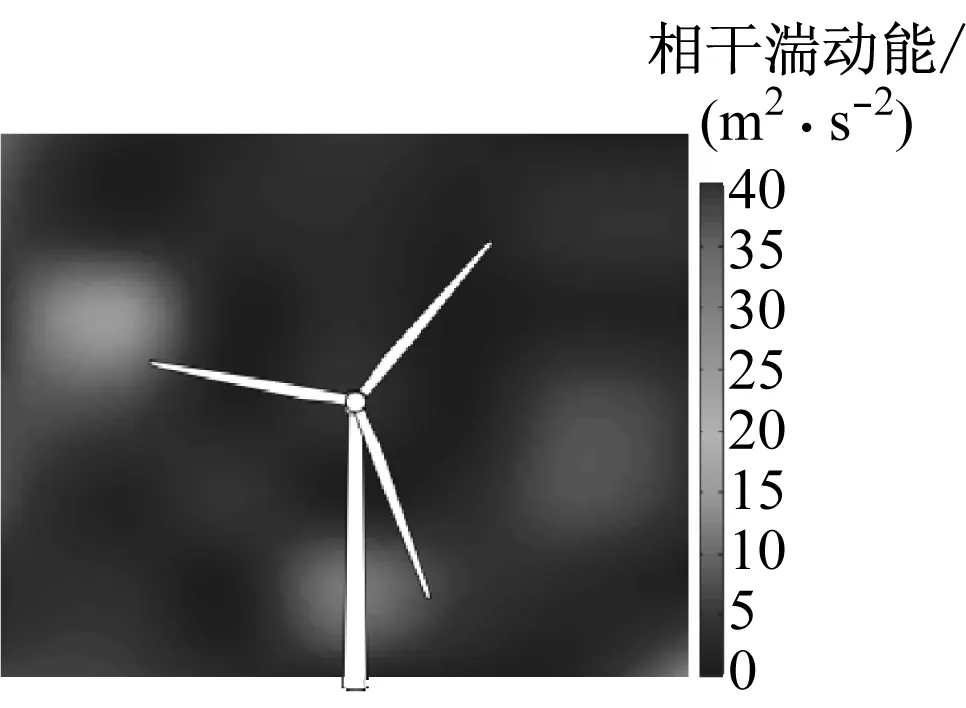
(c)t=300 s相干湍动能

(d)t=300 s相干湍动能(加入相干结构)
图3加入相干结构前后速度及相干湍动能的对比
Fig.3Comparison of wind speed and CTKE with and without coherent structures
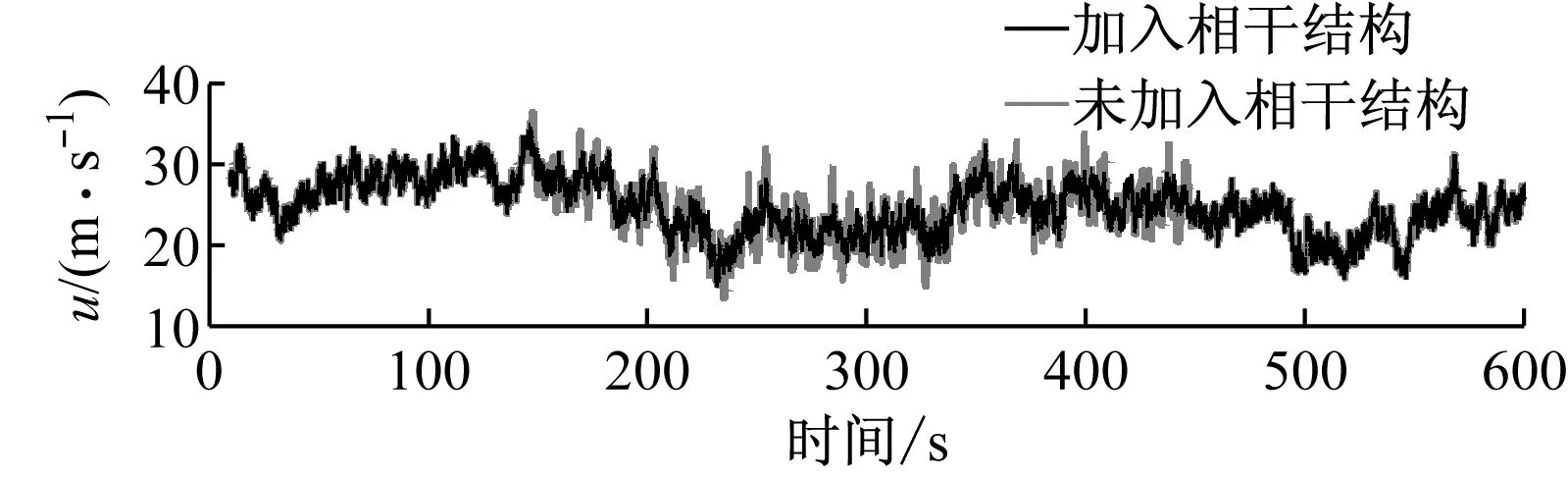
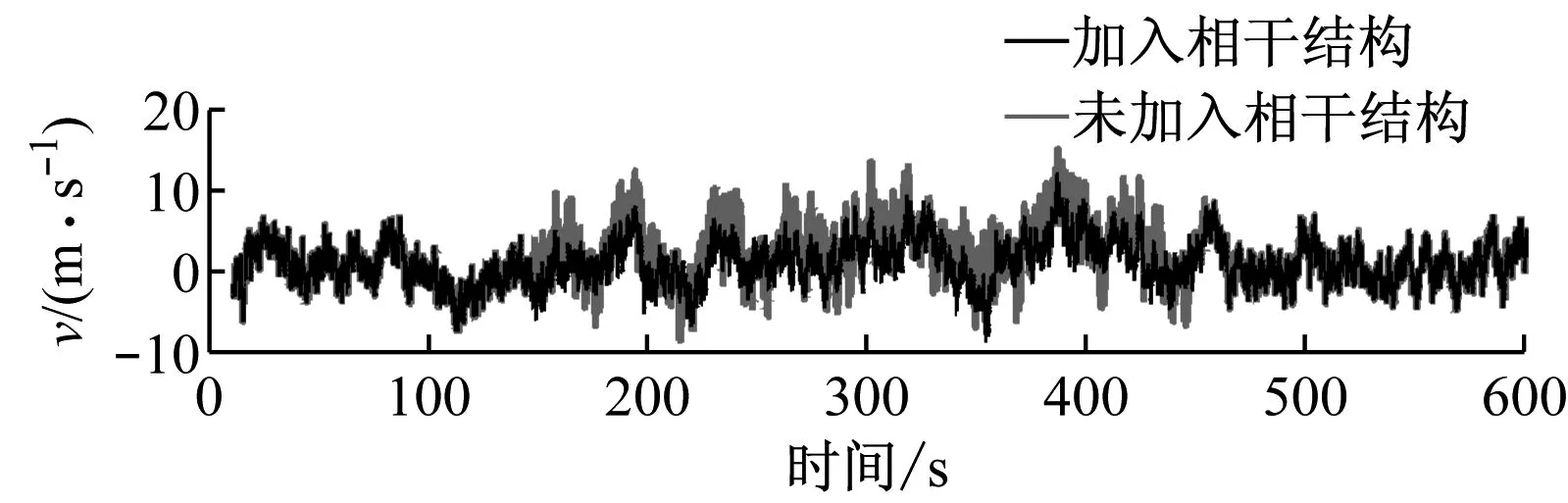

(a) 风速分量

(b) 相干湍动能
2 计算流程和计算工况
2.1计算流程
模态截断法与多体动力学相结合的计算方法是目前实现风力机结构动力学仿真的主流方式之一.该方法假设风力机为有限个刚性体和柔性体的组合系统,通过形函数描述风力机柔性体的模态振型,减少风力机自由度数目至已考虑的模态数,从而加快气动结构耦合计算速度.其中,由NWTC针对水平轴风力机研发的开源软件FAST[18]应用最为广泛.
FAST为时域求解风力机结构动力学响应的CAE软件,主要包含3个模块:气动模块、弹性模块和伺服模块.其中,气动模块采用Pitt-Peters加速度势动态入流理论来求解风轮平面诱导速度;考虑Prandtl叶尖损失及叶轮损失,通过叶素动量理论结合翼型静态气动特性求解风轮气动力,若需要翼型动态气动特性,则通过Beddoes-Leishman动态失速模型修正.在弹性模块中,通过Kane方法建立多体动力学模型,将风力机视为由叶片、低速轴和塔架等柔性体及轮毂、变速箱、高速轴、发电机和机舱等刚性体组成的多结构体系统.采用模态截断法描述叶片和塔架等柔性连续体弹性变形,假设其结构变形为一系列振动模态的线性叠加.以气动模块求解的风轮气动力作为输入激励,得到该时间步的结构动力学及运动学响应并反馈至伺服模块和气动模块.伺服模块则根据弹性模块反馈信息作出相应的控制指令,主要包括调节叶片桨距角、风轮转速和高速轴转速等.具体动力学仿真流程如图5所示,其中Tmax为仿真时间,dt为时间步长.

图5 动力学仿真流程图
2.2计算工况
计算工况包括正常运行工况和偏工况,其中正常运行工况仅采用变速变桨距控制,偏工况包括3种典型运行状态,即偏航、紧急停机和一直停机.具体计算工况见表2,分别计算正常运行工况和偏工况有无相干结构时的动态响应,共8个工况.
3 结果分析
3.1正常运行工况
图6为风力机正常运行工况下加入相干结构前后的叶根面外弯矩、塔尖侧向弯矩和塔基侧向弯矩的时域动态响应.由图6可知,加入相干结构后,各响应变化均更加剧烈,叶根弯矩幅值变化范围由-4 024~9 180 kN·m增大至-4 024~9 462 kN·m;塔尖弯矩的最大值则由5 181 kN·m增大至5 751 kN·m,最小值由3 192 kN·m降低至2 072 kN·m,标准差则增大49.1%;塔基弯矩则更为敏感,波动幅度增大1.96倍,最大值和最小值分别增大45%和-256%,标准差增大115%.加入相干结构的一段时间内动态响应剧烈程度明显加剧.
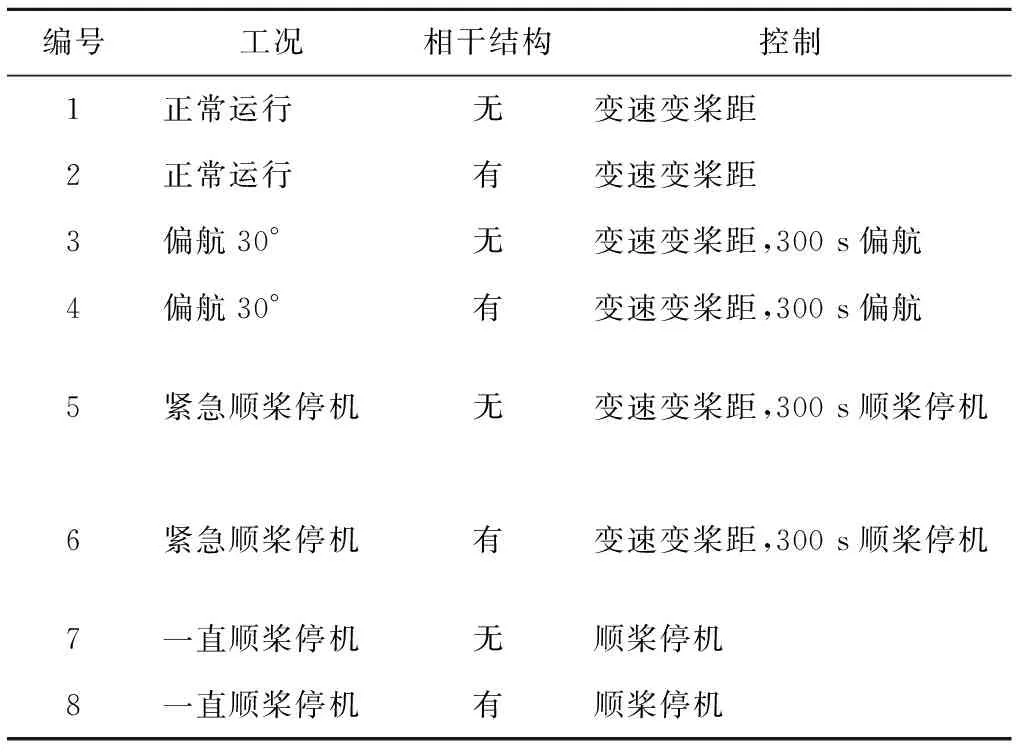
表2 具体计算工况
相干结构对叶片载荷影响相对较小,但风轮-塔
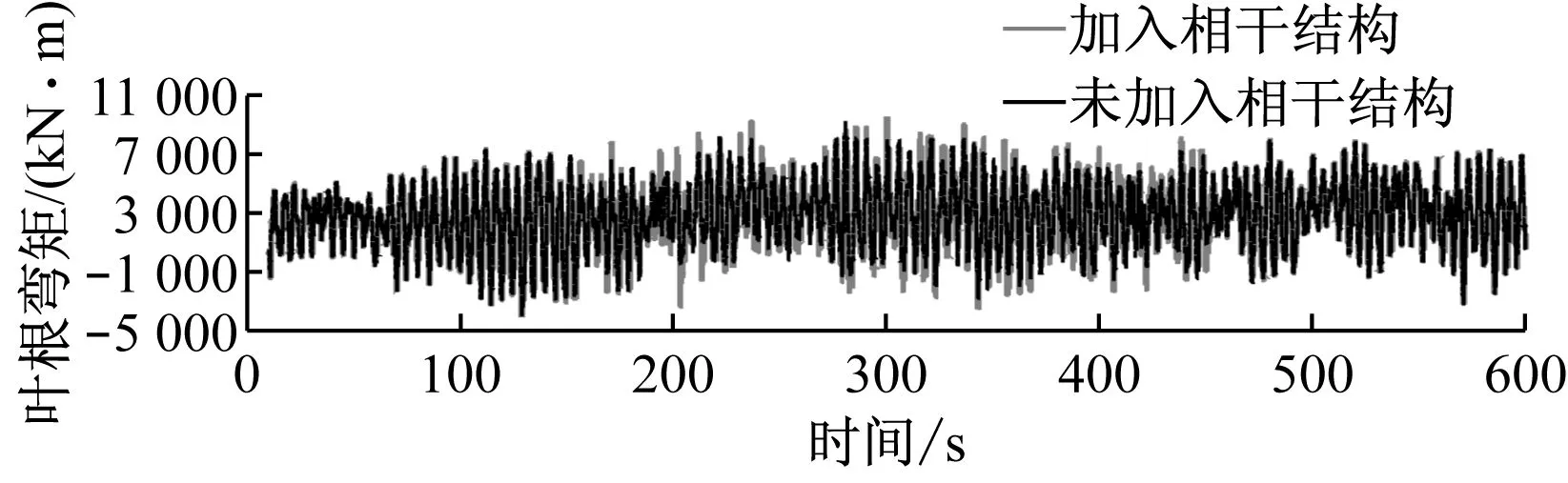
(a) 叶根面外弯矩

(b) 塔尖侧向弯矩
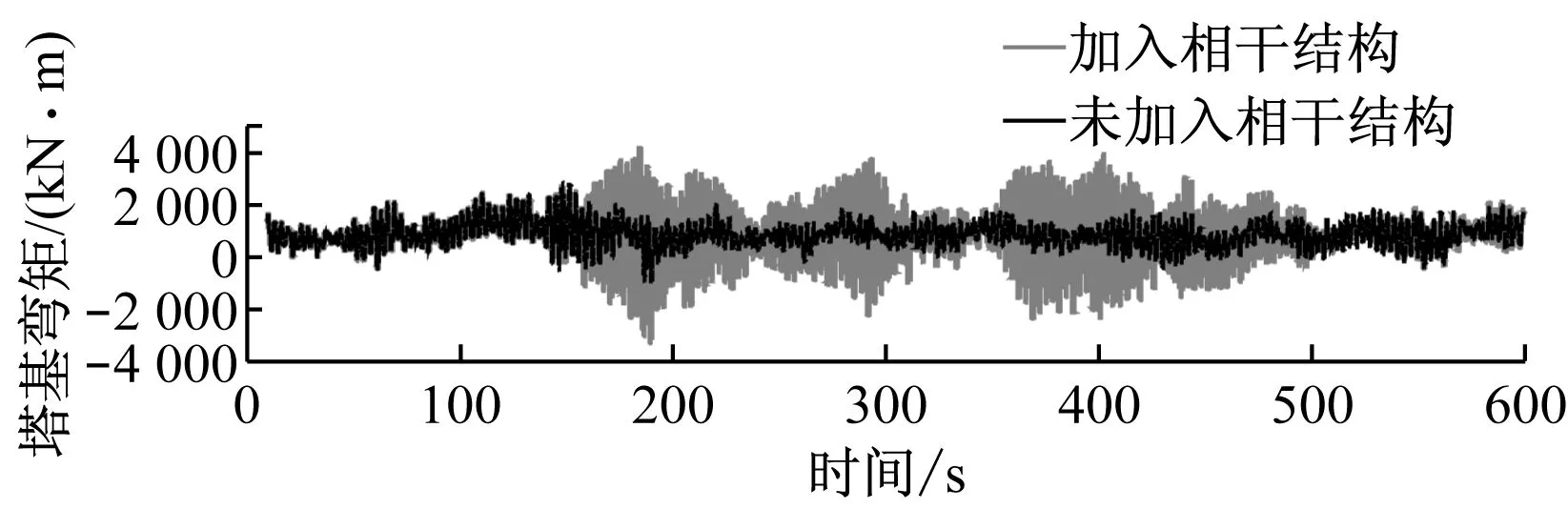
(c) 塔基侧向弯矩
Fig.6Dynamic responses in time domain with and without coherent structures under normal conditions
架-机舱耦合系统则对相干结构的加入引起的风速变化更加敏感.由于风速为不规则的脉动风速并已超过额定风速,且此时并未选择停机,风力机处于不断变桨的运行状态以输出额定功率,这种非稳定过程的载荷动态变化放大了载荷非线性传递过程,叶片载荷微弱的增大导致塔架载荷的急剧上升,尤其是塔基载荷.
图7为正常运行工况下,加入相干结构前后叶根面外弯矩、塔尖侧向弯矩和塔基侧向弯矩的频域响应.图7(a)表明叶根弯矩响应在0.2 Hz出现明显的峰值,说明载荷的主要刺激频率为0.2 Hz,相干结构对载荷主要刺激频率的影响较小.塔尖弯矩响应频率区段为0.001~0.18 Hz、0.28~0.34 Hz、0.57 ~0.64 Hz和1.61 ~1.69 Hz,其中0.32 Hz处出现明显峰值,2个相对较低的频段为主要刺激频率.加入相干结构后4个频段响应均不同程度增大,0.32 Hz频率附近出现明显震荡,且峰值增大1倍.塔基弯矩的响应峰值同样在0.32 Hz附近出现,为最主要刺激频率,加入相干结构后在0.32 Hz附近震荡明显,峰值增大1倍.
频域结果则表明,风轮旋转频率0.2 Hz为叶片载荷的主要刺激频率,相干结构对叶片载荷影响较小.塔架载荷和机舱响应的刺激频率则集中在塔架一阶侧向振动频率0.32 Hz附近,0 Hz附近频段的塔尖弯矩响应不可忽略,加入相干结构后0.32 Hz附近塔架载荷的响应峰值增大1倍.
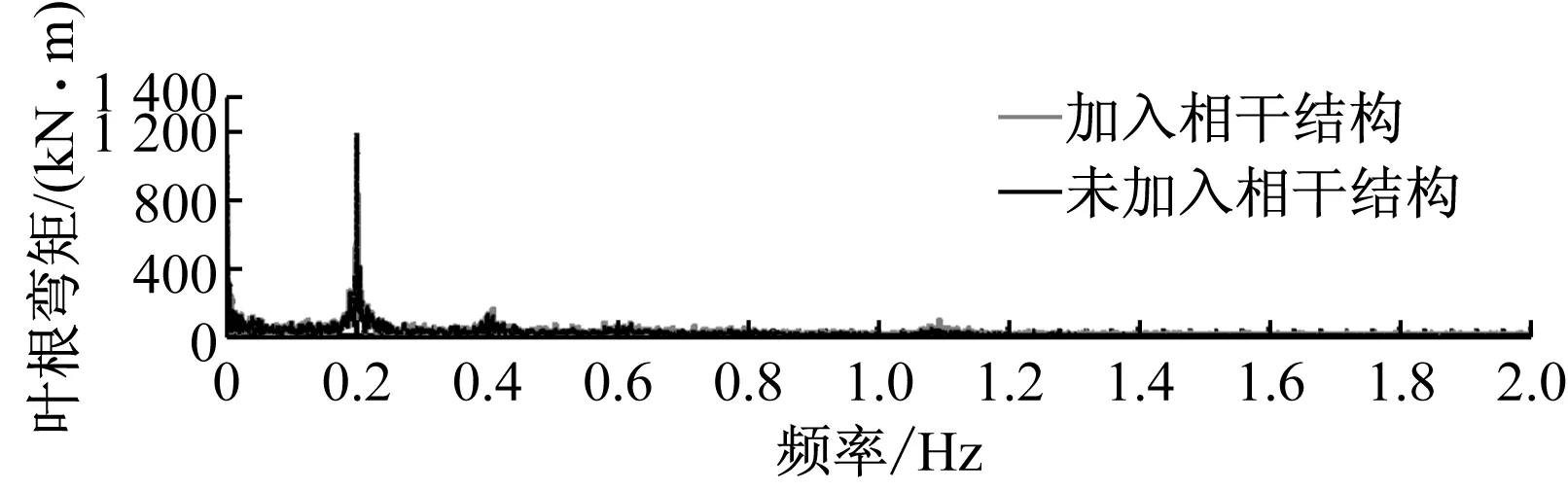
(a) 叶根面外弯矩
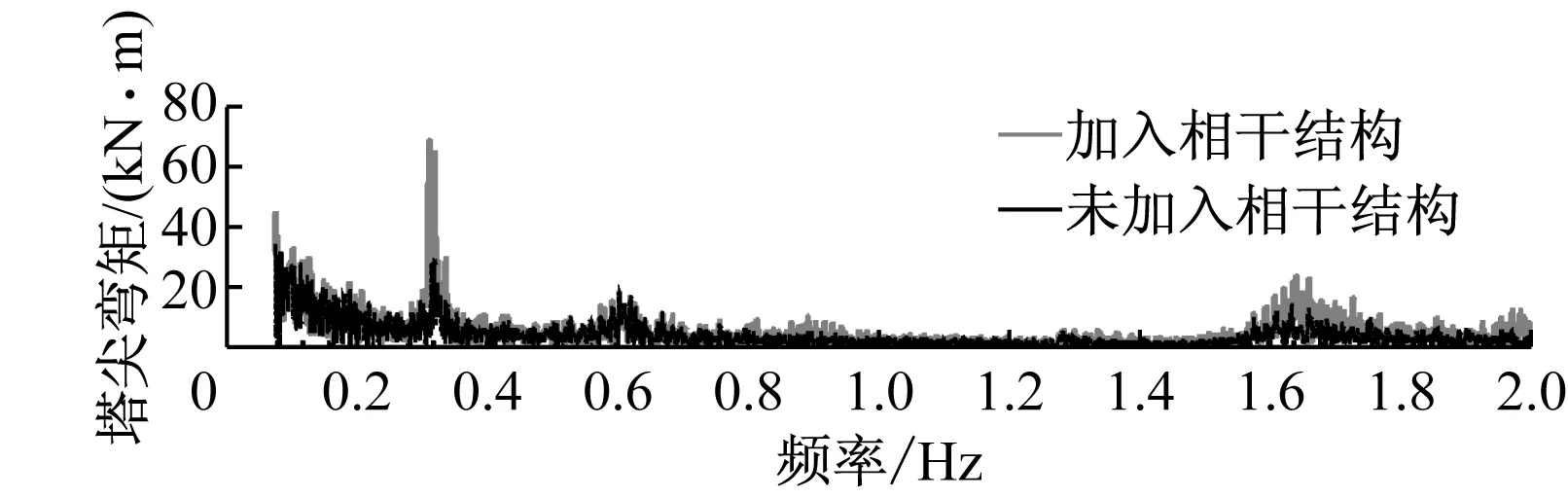
(b) 塔尖侧向弯矩
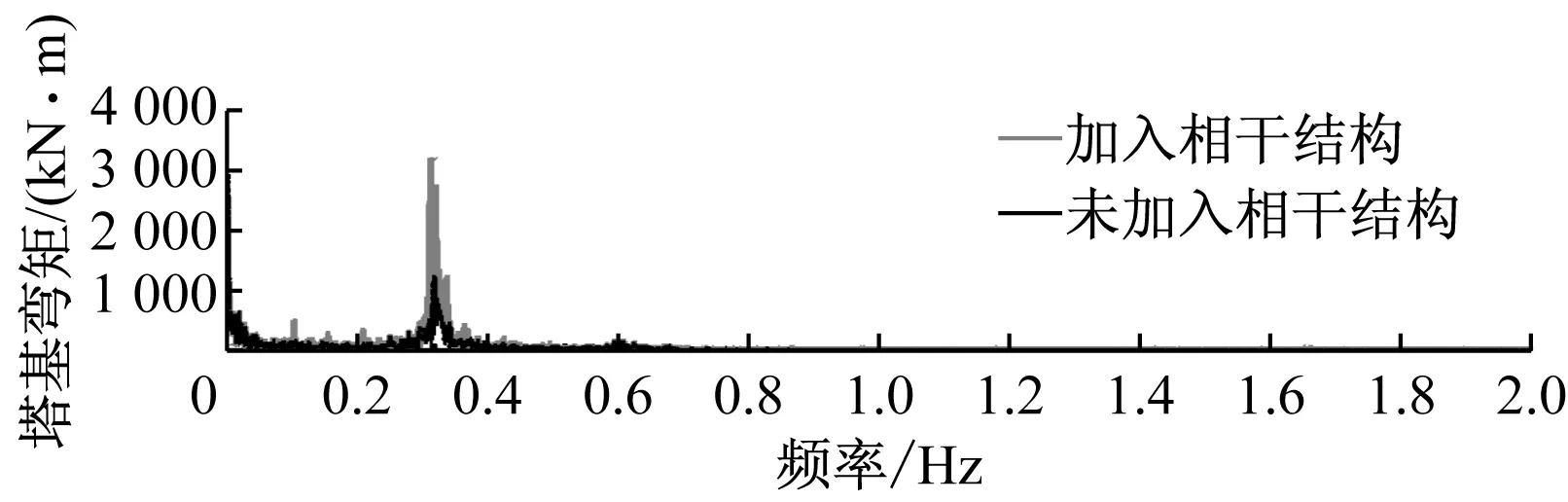
(c) 塔基侧向弯矩
Fig.7Dynamic responses in frequency domain with and without coherent structures under normal conditions
3.2偏工况
除正常运行工况外,分别计算了动态偏航30°、紧急顺桨停机和一直顺桨停机3种偏工况.图8为3种工况下塔尖弯矩在加入相干结构前后的动态响应.

(a) 偏航30°工况

(b) 紧急顺桨停机工况
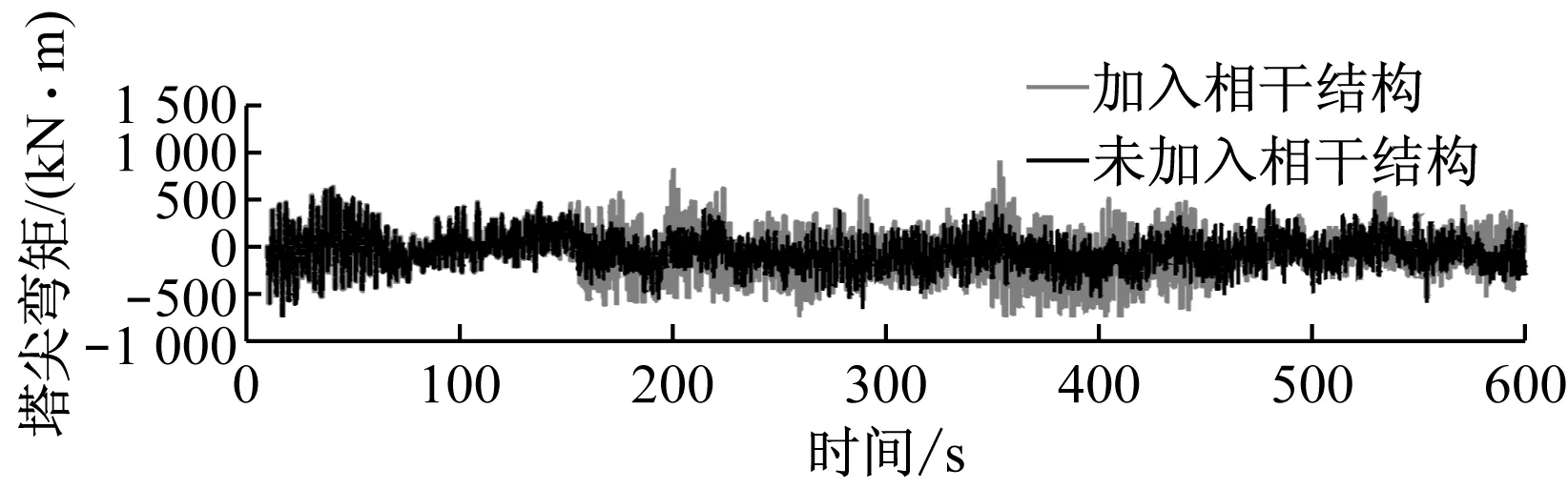
(c) 一直顺桨停机工况
Fig.8Dynamic responses of tower tip moment in time domain under different operation conditions
由图8(a)可知,未加入相干结构、第300 s开始偏航运动时塔尖弯矩出现急剧下降,约10 s后下降至0左右,并迅速回升至2 000 kN·m,之后载荷变化比偏航前略微剧烈;加入相干结构的工况与未加入相干结构时类似,但幅值相对更大,偏航运动结束后,最小值达到-2 000 kN·m.
图8(b)表明,紧急停机后塔尖弯矩急剧下降,在0值附近以±2 000 kN·m左右的振幅大范围波动,约10 s后逐渐缩小变化幅度,加入相干结构对其影响相对较小,略微增大了载荷变化范围,450 s后相干结构影响逐渐减小至可忽略量级.
图8(c)表明,加入相干结构后,塔尖弯矩在一直停机工况下的变化更加剧烈,其波动范围相对增大1倍左右,450 s后相干结构的影响逐渐减小.
相干结构在偏航工况下对塔尖弯矩的影响是永久性的,且加剧了载荷的变化,对紧急停机和一直停机工况的影响为暂时性的,短时剧烈变化后幅值响应逐渐恢复至未加入相干结构工况水平.
4 结 论
(1) 在普通湍流风基础上加入相干结构,有效加剧风速变化,一定程度上可代表强湍流度风况,可模拟速度和方向均剧烈变化的风况.
(2) 加入相干结构后的湍流风场,其轮毂点处相干湍动能的最大值增大49%,平均值增大38%,风场紊流度增大.
(3) 相较于普通湍流风工况,加入相干结构的工况,其叶根弯矩、塔尖弯矩和塔基弯矩时程响应波动幅度均出现不同程度的增加,其中塔基弯矩最为敏感,波动幅度增大1.96倍;叶根弯矩的主要刺激频率为风轮旋转频率0.2 Hz,相干结构对其影响较小.塔尖弯矩和塔基弯矩响应的特征频率则在0.32 Hz左右,为塔架一阶固有频率.
(4) 加入相干结构对偏航工况影响较大,在偏航时受不稳定载荷影响,其动态响应剧烈程度增加,降低幅度达到50%左右,对紧急停机和一直停机工况的影响相对较小,且为暂时性影响,短时加剧后逐渐减小至未加入相干结构水平.
[1]陈严,张锦源,王楠,等.风力机风场模型的研究及紊流风场的MATLAB数值模拟[J].太阳能学报,2006,27(9):955-960.
CHEN Yan,ZHANG Jinyuan,WANG Nan,etal.Wind turbine wind field models study and numerical simulation of turbulence wind field with MATLAB[J].Acta Energiae Solaris Sinica,2006,27(9):955-960.
[2]岳一松,蔡旭. 风场与风力机模拟系统的设计与实现[J]. 电机与控制应用,2008,35(4):17-21.
YUE Yisong, CAI Xu.Design and actualization of wind farm and wind turbine imitation system[J]. Electric Machines & Control Application, 2008, 35(4): 17-21.
[3]陈晓明.风场与风力机尾流模型研究[D].兰州:兰州理工大学,2010.
[4]BOSSANYI E. Short-term stochastic wind prediction and possible control applications[C]//Proceedings of the Delphi Workshop on Wind Energy Applications. Greece: European Cultural Center of Delphi, 1985.
[5]KARINIOTAKIS G, NOGARET E, STAVRAKA-KIS G. Advanced short-term forecasting of wind power production[C]// 1997 European Wind Energy Conference. Ireland: Slane County Meath, 1997.
[6]NIELSEN T S, MADSEN H, TOFTING J. Experiences with statistical methods for wind power prediction[C]// 1999 European Wind Energy Conference. France: Routledge, 1999.
[7]MOHANDES M A, HALAWANI T O, REHMAN S,etal. Support vector machines for wind speed prediction[J]. Renewable Energy, 2004, 29(6): 939-947.
[8]DAMOUSIS I G, ALEXIADIS M C, THEOCHARIS J B,etal. A fuzzy model for wind speed prediction and power generation in wind parks using spatial correlation[J]. IEEE Transactions on Energy Conversion, 2004, 19(2): 352-361.
[9]BILGILI M, SAHIN B, YASAR A. Application of artificial neural networks for the wind speed prediction of target station using reference stations data[J]. Renewable Energy, 2007, 32(14): 2350-2360.
[10]SHIRAZI M, JAGER D, WILDE S,etal. Lamar low-level jet project interim report[R]. Golden, Colorado, USA: National Renewable Energy Laboratory, 2004.
[11]HØJSTRUP J. Velocity spectra in the unstable planetary boundary layer[J]. Journal of the Atmospheric Sciences, 1982, 39(10): 2239-2248.
[12]OLESEN H R, LARSEN S E, HØJSTRUP J. Modelling velocity spectra in the lower part of the planetary boundary layer[J]. Boundary-Layer Meteorology, 1984, 29(3): 285-312.
[13]KELLEY N, HAND M, LARWOOD S,etal. The NREL large-scale turbine inflow and response experiment: preliminary results[C]//ASME 2002 Wind Energy Symposium. Neno, Nevada, USA: American Society of Mechanical Engineers, 2002: 412-426.
[14]MONIN A S, OBUKHOV A M. Basic laws of turbulent mixing in the surface layer of the atmosphere[J]. Trudy Geofizicheskogo Instituta Akademiya Nauk SSSR, 1954, 24(151): 163-187.
[15]BURTON T, SHARPE D, JENKINS N,etal. Wind energy handbook[M]. New York:John Wiley & Sons, 2001.
[16]SOLARI G. Turbulence modeling for gust loading[J]. Journal of Structural Engineering, 1987, 113(7): 1550-1569.
[17]KELLEY N D, JONKMAN B J, SCOTT G N,etal.The impact of coherent turbulence on wind turbine aeroelastic response and its simulation: preprint[C]// Windpower 2005 Conference Proceedings.USA: American Wind Energy Association,2005.
[18]安利强,孙少华,周邢银. 发电机故障时海上风电机组动态特性分析[J].动力工程学报,2014,34(11):891-896.
AN Liqiang, SUN Shaohua, ZHOU Xingyin. Analysis on dynamic characteristics of offshore wind turbines with generator faults[J]. Journal of Chinese Society of Power Engineering, 2014, 34(11): 891-896.
Structural Dynamic Response of a Wind Turbine Under High-speed Strong Turbulence Inflow Conditions
YANGYang1,LIChun1,2,MIAOWeipao1,YEKehua1,YEZhou1,2
(1. School of Energy and Power Engineering, University of Shanghai for Science and Technology,Shanghai, 200093, China; 2. Shanghai Key Laboratory of Multiphase Flow and Heat Transfer in Power Engineering, Shanghai 200093, China)
To analyze the structural dynamic response of large-scale wind turbines operating under high-speed strong turbulence inflow conditions, a three-dimensional extreme turbulence flow field with an average wind speed of 25 m/s was established based on NWTCUP wind spectrum. By adding the coherent structures deduced from the scaling numerical results of Kelvin-Helmholtz instable flow to the background wind to represent an inflow condition of higher turbulence intensity, the structural dynamic response of the wind turbine respectively with coherent inflow and normal turbulence flow fields were calculated in FAST code under three off-design conditions, such as yaw to 30°, emergency shutdown and parked cases, etc. Results show that coherent structures enhance the changes of wind speed in space-time domain, with increased kinetic energy of coherent turbulence (CTKE), suitable for representing the case of higher turbulence intensity; while coherent structures promote the dynamic response of wind turbine, especially on the bending moment of tower base, with the variation range of response amplitude expanded by 1.96 times. The stimulus frequency of root bending load is the frequency of wind wheel rotation, while the response of both tower load and nacelle motion is of the first-order natural frequency of side to side vibration. Coherent structures have greater impact on the tower tip moment under off-design conditions, and the non-stationary fluctuations becomes significant during yawing, emergency shutdown and other non-steady operation periods.
wind turbine; turbulence wind field; coherent structure; dynamic response; off-design condition
2015-08-17
2015-09-09
国家自然科学基金资助项目(51176129);上海市教育委员会科研创新(重点)基金资助项目(13ZZ120,13YZ066);教育部高等学校博士学科点专项科研基金(博导类)资助项目(20123120110008);上海市科委资助项目(13DZ2260900)
杨阳(1992-),男,江西樟树人,博士生,研究方向为风力机气动弹性仿真.
李春(通信作者),男,教授,博导,电话(Tel.):021-55271729;E-mail:lichun_usst@163.com.
1674-7607(2016)08-0638-07
TK83
A学科分类号:480.60
