基于集成深度玻尔兹曼机和最小二乘支持向量回归的燃烧过程NOx预测算法

李　楠，　卢　钢，　李新利，　闫　勇,

(1．华北电力大学 控制与计算机工程学院,北京 102206；2．英国肯特大学 工程与数字艺术学院，坎特伯雷，肯特 CT2 7NT 英国)



基于集成深度玻尔兹曼机和最小二乘支持向量回归的燃烧过程NOx预测算法

李楠1，卢钢2，李新利1，闫勇1,2

(1．华北电力大学 控制与计算机工程学院,北京 102206；2．英国肯特大学 工程与数字艺术学院，坎特伯雷，肯特 CT2 7NT 英国)

火焰自由基图像； 深度玻尔兹曼机； 最小二乘支持向量回归； NOx预测

在未来较长一段时期内，以化石燃料和生物质为主要能源的火力发电依旧是造成大气污染的主要因素，特别是氮氧化物(NOx)的排放对环境恶化和居民健康造成了直接影响[1].许多国家为此制订了相应的节能环保政策来降低污染物对环境的影响，如我国制订了《锅炉大气污染物排放标准》[2].因此，研究燃烧优化，预测并降低燃烧污染物排放就尤为重要.但NOx的生成机制非常复杂，与燃料类型、炉体型式、燃烧器结构、炉内温度、过量空气系数、固体燃料(煤粉或生物质)细度和配风方式等很多因素有直接关系.因此,许多研究人员都在探索有效的NOx预测技术和方法.

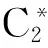
目前的研究很少涉及火焰自由基图像的特征学习过程.为了从火焰自由基图像数据中学习到更为稳健的图像特征，笔者提出应用深度玻尔兹曼机(Deep Boltzmann Machine，DBM)进行特征提取.DBM在国家标准技术局(MNIST)数据库的识别上具有优秀的分类能力，其对图像集合进行无监督特征学习的能力得到了肯定[11-12].使用DBM从火焰自由基图像集中学习到的特征是否能够用于NOx预测尚无研究.笔者通过DBM从火焰自由基图像集学习得到其特征后，集成最小二乘支持向量回归，建立了NOx预测模型.

1　NOx预测算法的建立

1.1基于DBM模型的图像特征学习

自从2006年深度学习取得突破进展后，深度学习的相关算法已经成为信号/图像模式识别相关研究和应用的热门方向[11].相较于现存的机器学习算法，深度学习在无监督特征提取这一方面更为恰当.深度玻尔兹曼机[12]是深度学习中较为重要的一类生成模型,该模型由多个受限玻尔兹曼机(Restricted Boltzmann Machine，RBM)堆叠组成一个阶层式的网络结构，每一层的RBM由无监督贪婪算法进行训练.图1给出了DBM的训练过程框图，其训练过程可归纳为以下2点.

(1) 根据可见层状态v来得到隐含层状态h，这个过程的建模[12]如下：

(1)

(2)

(2) 通过隐含层状态h重构可见层状态得到v*，这个过程的建模如下：

(3)

(4)

式中：P(·|·)为条件概率；Wij为连接DBM网络的权重；j为权重；aj和bi为偏置项.

图1　DBM训练过程框图

虽然RBM的可见层和隐含层在层内无连接，但是层间有连接.当给定了可见层状态v时，隐含层单元的激活状态h是相互独立的；反之，给定隐含层状态h，各可见层单元的状态v也是相互独立的，这使得特征学习中涉及的概率分布计算更为便捷.而DBM的无监督特征学习就是通过这种学习方式阶层式的得以实现.

1.2集成最小二乘支持向量回归的NOx预测

1.2.1最小二乘支持向量回归

(5)

式中：φ(x)为非线性映射，其将输入空间映射到一个高维的特征空间；e为权重向量；d为偏置项.

将上述问题转换为求解线性方程组，并表达为如下优化问题：

(6)

式中：γ为惩罚系数；ξi为松弛变量.

LSSVM的最终解可表示为

(7)

式中：ci为拉格朗日乘子;K(*)为核函数.

当LSSVM用于求解回归问题时，上述求解过程被称为最小二乘支持向量回归(LeastSquare-SupportVectorRegression，LSSVR).笔者在之前的研究中验证了高斯径向基函数作为核函数的LSSVR相较于其余的机器学习算法更适于拟合图像特征与NOx排放量的关系[9],因此采用LSSVR建立预测模型.高斯径向基函数的定义如下：

(8)

式中：σ为核参数.

1.2.2NOx预测算法

图2为NOx预测算法的示意图.当给定火焰自由基图像的训练集合(包含p个样本)和测试集合(包含q个样本)，NOx预测算法可归纳如下：

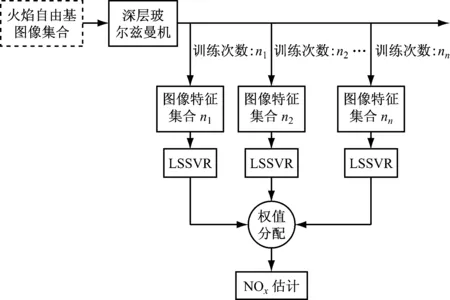
图2　NOx预测算法示意图

(9)

式中:ui为权值.

2　实验结果与分析

2.1火焰自由基图像集与NOx检测

燃烧实验在小型生物质-燃气燃烧实验装置上进行.火焰自由基图像由一个光增强成像系统[15]获得.主要的燃料是生物质(柳木)和丙烷.柳木的工业分析见表1[16]，当柳木被研磨成细微颗粒后，由旋转给料机送入燃烧器.通过改变给料机的转速(10～40 Hz，以5 Hz为间隔)，总共产生7组燃料质量流量，即7种测试条件.丙烷的体积流量被固定为0.6 L/min.在每种测试条件下，每种火焰自由基拍摄100幅图像，4种火焰自由基图像同时被成像系统获取.图3给出了4种火焰自由基图像的示例.

表1　柳木的工业分析

(a)OH*(308 nm)

(b)CN*(387 nm)

(c)CH*(432mm)

(d)(514mm)

图3火焰自由基图像

Fig.3Flame radical images

在拍摄火焰自由基图像过程中，采用KANE 900 PLUS烟气分析仪来采集烟气中的NOx排放值.每种测试条件下采集3次NOx排放值，将其均值作为预测模型的参考值.火焰自由基图像与NOx排放参考值组成了一个完备的标签数据集合.该标签数据集合包含了700个样本，将其划分为训练集和测试集，其中训练集(420个样本)用来训练NOx的预测模型，测试集(280个样本)用来检验预测模型的预测效果.

在通常的固体燃料(特别是生物质)燃烧温度下，燃料型NOx中的挥发分NOx占很大比例(也有少量焦炭NOx).研究表明,在氧化性气氛中，随着过量空气系数的增大，挥发分NOx在燃料型NOx中占的比例远超过焦炭NOx[17].且与煤焦相比，生物质焦具有更加良好的还原性，对焦炭NOx的生成有一定的抑制作用[18].考虑到本实验是在小型试验炉上使用挥发分较高的生物质燃料(表1)，因此烟气分析仪检测的NOx可视为挥发分NOx(即焦炭NOx可以忽略不计).但在实际锅炉燃烧中，2种NOx都应考虑.

2.2NOx预测算法稳定性分析及其预测结果

DBM可以对给定的图像集进行无监督的特征学习，学习过程的不唯一性使得学习到的图像特征集合具有随机性：(1)将训练DBM的无监督贪婪方法设置相同的训练次数，进行多次独立的特征学习，获取的图像特征集合是不同的；(2)设置不同的训练次数进行独立的特征学习，可以发现得到的图像特征集合也是不同的.为分析图像特征集合的随机性对NOx预测结果的影响，采用如下计算方法：将训练次数设置为10，独立训练50次DBM，可以得到50个独立的随机图像特征集合；采用LSSVR计算这50个图像特征集合对应的NOx排放预测值，根据所得NOx排放预测值计算对应的50个均方根误差，之后训练次数以10为间隔递增，到100截止，重复上面的计算.

(10)

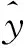
图4给出了依据上述计算方法得到的均方根误差的变化曲线.由图4可知，随着训练次数的增加，均方根误差的数值变化并无规律性，但有上限.因此，可以认为在不同的训练次数下，依据DBM学习的图像特征集合得到的NOx排放预测值具有随机性，这也是NOx预测算法中需要集成多个LSSVR进行计算的原因.此外，当DBM的训练次数固定时，测试中均方根误差的最大标准差为0.74 mg/m3，对应训练次数为60，均方根误差的最小标准差为0.02 mg/m3,对应训练次数为20.图4中均方根误差的数值是在一个较小的范围内变动的，因此可以认为虽然训练次数相同时得到的图像特征集合具有随机性，但是相应的NOx排放预测值是稳定的.

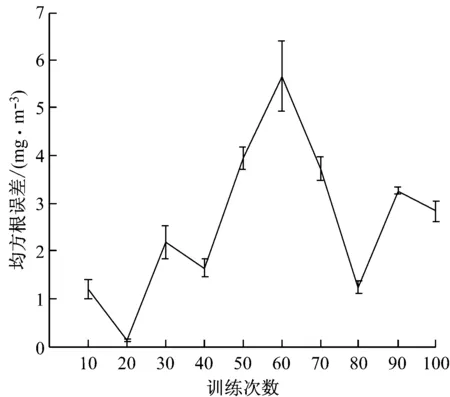
图4　不同图像特征集合的预测结果的均方根误差

Fig.4RMSE values of prediction results for different image feature sets

另外，在第1.2节提出的NOx预测算法中，设置DBM的总训练次数为100，在区间[1,100]内进行50次独立随机抽样.图5给出了根据相应预测结果得到50个均方根误差值.由图5可知，最大的均方根误差对应第35次抽样，其值为1.81 mg/m3；最小的均方根误差对应第1次抽样，其值为0.82 mg/m3；均方根误差均值为1.35 mg/m3，距离均方根误差均值最近的为第40次抽样，其值为1.33 mg/m3.表2给出了这3组抽样在每种测试条件下的NOx排放预测值相对误差的最大值.表2中，对于每一纵列，当燃料质量流量给定时，3组典型抽样对应的相对误差较小，这说明预测结果是稳定的.

图5　50次随机抽样的预测结果的均方根误差

由于第40次抽样对应的均方根误差在数值上最接近50次独立预测得到的均方根误差均值，因此图6给出了第40次抽样对应的NOx排放预测值的相对误差.由图6可知，根据测试样本计算得到的280个NOx排放预测值中，共有274个NOx排放预测值的相对误差分布在±2%，而不在±2%的6个NOx排放预测值为测试条件1中的4个值，相对误差分别为7.7%、2.5%、5.7%和3.4%；测试条件3中的一个值，相对误差为4.7%；测试条件4中的一个值，相对误差为3.8%.这些NOx排放预测值均没有显著偏离每种测试条件下的NOx排放参考值，说明预测结果精度较高.这一方面是因为DBM提供了良好的特征学习，使得测试集与训练集的特征相似度高；另一方面是因为算法集成了多个LSSVR，降低了预测结果的随机性.因此可以认为算法的预测结果稳定.

表23组典型抽样对应的NOx排放预测值相对误差的最大值

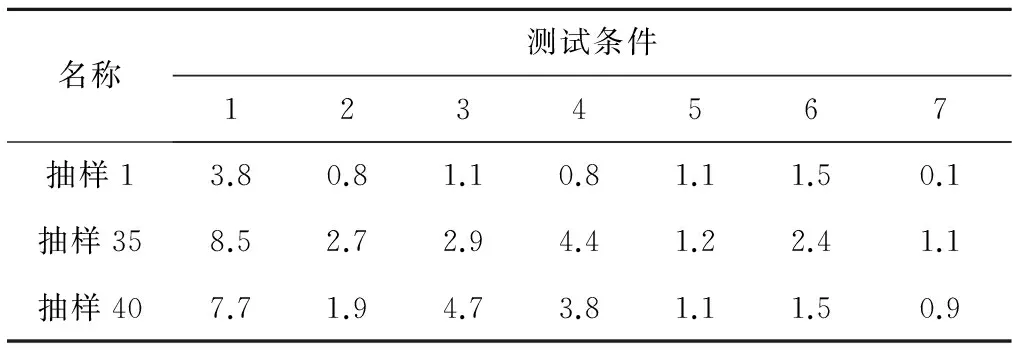
Tab.2　Maximum relative errors of NOx emission prediction for three typical samplings %

图6　NOx排放预测值的相对误差

2.3不同NOx预测算法之间的比较分析

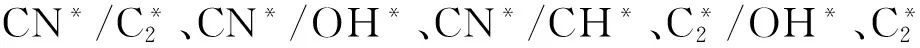
图7给出了上述4种预测算法以及本文预测算法的比较结果.从图7可以看出，本文预测算法得到的均方根误差在数值上显著低于其他4种预测算法，这源于DBM提供了良好的图像特征，阶层式地对火焰自由基图像进行了算法统计建模.基于IR算法和IC算法计算得到的均方根误差值较高，因为这2类图像特征只提供了不完全的统计描述，且仅考虑了火焰自由基图像灰度值这个因素，却完全忽略了自由基图像的面积；当燃烧情况比较剧烈时，火焰自由基图像的灰度均值也会有较大的变化波动，从而导致较大的预测偏差.CTZM算法和NMF-TA算法都是利用预先设定的数学公式计算图像的特征，它们不能像DBM一样根据图像集合的特点自动学习图像特征，因此二者的预测结果劣于本文预测算法.

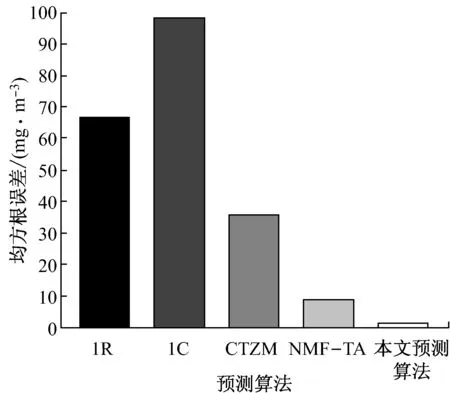
图7　各预测算法均方根误差值的比较

对于真实的锅炉燃烧环境，虽然由于燃料类型、燃烧器结构和配风等因素会导致获取的火焰自由基图像形状发生较大变化，但预测模型中的特征学习过程确保了所提取的火焰自由基图像特征可以根据所获取的图像进行调整，而且预测模型是数据驱动的，相应图像特征与对应的NOx的变化都将直接反映在所构建的NOx预测模型中，从而降低了预测误差.但是在实际的燃烧过程中，自由基形状变化对NOx生成的实际影响程度还需进一步量化研究，特别是燃料型NOx中焦炭NOx的生成对NOx预测模型的影响.

3　结　论

通过对火焰自由基图像与NOx排放关联性的研究，提出了一种基于自由基图像的集成深度玻尔兹曼机和最小二乘支持向量回归的NOx预测算法.在小型生物质-气体燃烧试验炉中的实验结果表明，NOx排放预测值与烟气分析仪测量的NOx排放参考值具有较好的一致性，且预测结果稳定.与已有的基于火焰自由基图像特征的NOx预测算法相比，本文算法的预测结果更加准确，测试集对应的NOx排放预测值的相对误差几乎分布在±2%.这些结果表明了所提算法的实用性，对于基于火焰自由基图像法在实际锅炉燃烧中进行NOx准确预测具有一定指导意义.

[1]潘玲颖，麻林巍, 周喆，等.2030年中国煤电SO2和NOx排放总量的情况研究[J].动力工程学报，2010，30(5)：378-383.

PAN Lingying, MA Linwei, ZHOU Zhe,etal. Scenario analysis on total SO2and NOxemission of China's coal-fired power plants in 2030[J].Journal of Chinese Society of Power Engineering,2010, 30(5):378-383.

[2]中华人民共和国环境保护部.GB 13271—2014锅炉大气污染物排放标准[S].北京：中国环境科学出版社，2014：7-1.

[3]高芳，翟永杰，卓越，等.基于共享最小二乘支持向量机模型的电站锅炉燃烧系统的优化[J].动力工程学报，2012，32(12)：928-933.

GAO Fang, ZHAI Yongjie, ZHUO Yue,etal. Combustion optimization for utility boilers based on sharing LSSVM model [J]. Journal of Chinese Society of Power Engineering,2012,32(12): 928-933.

[4]牛培峰，肖兴军，李国强，等.基于万有引力搜索算法的电厂锅炉NOx排放模型的参数优化[J].动力工程学报，2013,33(2)：100-106.

NIU Peifeng, XIAO Xingjun, LI Guoqiang,etal.Parameter optimization for NOxemission model of power plant boilers based on gravitational search algorithm[J].Journal of Chinese Society of Power Engineering,2013,33(2):100-106.

[5]ZHOU Hao, CEN Kefa, MAO Jianbo. Combining neural network and genetic algorithms to optimize low NOxpulverized coal combustion [J].Fuel, 2001, 80(15):2163-2169.

[6]SANDROWITZ A K, COOKE J M, GLUMAC N G. Flame emission spectroscopy for equivalence ratio monitoring[J].Applied Spectroscopy,1998, 52(5): 658-662.

[7]BOMBACH R, KAPPELI B. Simultaneous visualisation of transient species in flames by planar-laser-induced fluorescence using a single laser system[J]. Applied Physics B, 1999, 68(2):251-255.

[8]李新利，李玲，卢钢，等. 基于火焰自由基成像和支持向量机的燃烧过程NOx排放预测[J]. 中国电机工程学报，2015，35(6)：1413-1419.

LI Xinli, LI Ling, LU Gang,etal. NOxemission prediction based on flame radical profiling and support vector machine[J]. Proceedings of the CSEE, 2015, 35(6):1413-1419.

[9]LI Nan, LU Gang, LI Xinli,etal. Prediction of pollutant emissions of biomass flames through digital imaging, contourlet transform, and support vector regression modeling[J]. IEEE Transactions on Instrumentation and Measurement, 2015, 64(9):2409-2416.

[10]LI Nan, LU Gang, LI Xinli,etal. Prediction of NOxemissions from a biomass fired combustion process through digital imaging, nonnegative matrix factorization and fast sparse[C]//Proceedings of the IEEE International Instrumentation and Measurement Technology Conference.Pisa, Italy: IEEE, 2015:176-180.

[11]DONG Yu, LI Deng. Deep learning and its applications to signal and information[J]. IEEE Processing of Signal Processing Magazine, 2011, 28(1):145-154.

[12]BENGIO Y. Learning deep architectures for AI[J]. Foundations and Trends®in Machine Learning,2009, 2(1):1-127.

[13]CORTES C, VAPNIK V. Support-vector networks[J]. Machine Learning, 1995,20(3):273-297.

[14]SUYKENS J A K, VANDEWALLE J. Least squares support vector machine classifiers[J]. Neural Processing Letters, 1999, 9(3):293-300.

[15]KRABICKA J, LU Gang, YAN Yong. Profiling and characterization of flame radicals by combining spectroscopic imaging and neural network techniques[J]. IEEE Transactions on Instrumentation and Measurement, 2011, 60(5):1854-1860.

[16]WILLIAMS A, JONES J M, MA L,etal. Pollutants from the combustion of solid biomass fuels[J]. Progress in Energy and Combustion Science, 2012, 38(2):113-137.

[17]白卫东.电站锅炉煤粉火焰安全监测及燃烧诊断方法研究[D].杭州：浙江大学，2004.

[18]柏继松.生物质燃烧过程氮和硫的迁移、转化特性研究[D].杭州：浙江大学，2012.

NOxEmission Prediction Based on Deep Boltzmann Machine Integrated with Least Square Support Vector Regression

LINan1,LUGang2,LIXinli1,YANYong1,2

(1. School of Control and Computer Engineering, North China Electric Power University,Beijing 102206, China; 2. School of Engineering and Digital Arts, University of Kent,Canterbury, Kent CT2 7NT, UK)

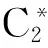
flame radical image; deep Boltzmann machine; least square support vector regression; NOxemission prediction

2015-09-11

国家重点基础研究发展计划资助项目(973 计划)(2012CB215203)；111引智资助项目(B13009)

李楠(1984-)，男，河南平顶山人，博士，主要从事机器学习、图像分析、污染物预测等方面的研究.电话(Tel.):15120028906；E-mail：smile_mokou@163.com.

1674-7607(2016)08-0615-06

X511

A学科分类号：610.30