波度和锥度对液体润滑机械密封空化特性影响

李振涛，郝木明，杨文静，韩婕，任宝杰

（中国石油大学（华东）密封技术研究所，山东 青岛 266580）



波度和锥度对液体润滑机械密封空化特性影响

李振涛，郝木明，杨文静，韩婕，任宝杰

（中国石油大学（华东）密封技术研究所，山东 青岛 266580）

为进一步探究机械密封液膜中空穴初生、演变等影响因素，基于质量守恒空化模型，建立考虑微观波度和锥度的液体润滑机械密封数学模型，采用有限控制体积法对控制方程进行离散，综合分析不同波幅、波数及锥度对空化特性的影响。结果表明：波度产生流体动压润滑效应，锥度产生流体静压润滑效应，两者共同影响空穴的初生和演变，而又影响空穴沿周向和径向的变化；空穴初生时，液膜破裂位置位于膜厚沿周向发散的低压区，且在空穴演变时其沿某一半径方向保持不变；量纲1波幅不超过0.5且波数不低于8或量纲1负锥度大于0.5的工况均可加快空化率，促进空化发生；而相同波幅且波数小于8或锥度趋向于正锥度的工况均可减缓空化率，有效抑制空化发生。

机械密封；液体润滑；波度；锥度；空化；有限控制体积法

DOI：10.11949/j.issn.0438-1157.20151733

引　言

因加工精度、压力变形或热变形等因素导致产生的表面形貌（如表面粗糙度、周向波度及径向锥度等）或各种型式激光加工微造型的客观存在，液膜润滑机械密封端面间产生大量的微观或宏观的间隙发散区和收敛区；而端面间液膜在发散区易产生压力下降，当压力降至低于密封介质的饱和蒸汽压时，液膜开始发生汽化，并形成汽泡和空穴，被称为空化现象［1-2］。空化现象对机械密封端面间液膜压力的分布、液膜承载能力及密封稳定性具有较大影响［3］。

Findley［4］于1968年最早提出机械密封中的空化问题，随后引起了国内外学者的重视并进行了多年的试验研究和理论研究。Nau［5］于1980年通过试验观测到机械密封中的空化现象，并用分析法确定空化区的边界；Khonsari等［6-7］对微造型端面密封进行可视化观察试验，观察到空化发生位置并且分析认为液膜厚度会影响空化初生，继而在研究空化效应对液膜承载力的研究中仅考虑了表面粗糙度和微造型结构尺寸等影响因素；孟凡明等［8］研究了机械密封或轴承端面微造型的幅值、分布位置及长宽比等结构参数对空穴机理的影响；Dowson等［9］介绍了求解液膜润滑控制方程的空化边界条件，即Sommerfeld、Half-Sommerfeld、Reynolds和JFO边界；其中，Sommerfeld边界为无空化边界，Half-Sommerfeld边界将计算结果中出现负压部分置为零，适用于第一次求近似解，而Reynolds边界应用最广但无法正确解释液膜再形成的过程，不满足质量守恒；Jakobsson等［10-11］提出的JFO边界很好地弥补了Reynolds边界存在的缺陷，满足质量守恒。胡纪滨等［12］采用质量守恒空化边界条件，研究了不同工况和槽深对径向直线槽端面密封的空化演变进行了数值模拟；郝木明等［13］采用数值计算方法研究了空化效应对螺旋槽液膜密封的稳态特性的影响。总之，目前在机械密封空化研究领域，绝大多数主要集中于对该现象的试验观察、端面微造型结构参数对空穴影响及空穴对密封润滑性能影响的分析；但在诱发空化发生影响因素领域，尤其是密封环端面微观形貌对其影响，未引起足够重视，研究不够深入。

鉴于上述存在的问题，本文基于质量守恒空化模型，建立考虑微观周向波度和径向锥度的液膜润滑机械密封数学模型，采用有限体积法对液膜润滑控制方程进行离散并通过Gauss-Seidel松弛迭代方法进行求解，以期获得微观波度和锥度对密封端面液膜中空穴初生、空穴区域演变及空化率等影响规律，为机械密封端面形貌参数优化设计提供参考。

1　数学模型与数值求解方法

1.1数学模型

机械密封典型结构如图1所示，当旋转环和静止环间形成的密封面处于纯液体润滑状态［14］时，弹簧压力和密封介质压力形成的闭合力与密封面间的液膜产生的开启力相平衡。

图1　机械密封结构和润滑模型Fig.1　Schematics of mechanical seal and lubrication model

假设在配对的旋转环和静止环中，一个密封面为光滑平面，另一个密封面具有各向同性的周向波度和径向锥度，密封面几何模型如图2所示。

对于图2所示的密封面间液膜总厚度定义为

式中，密封面内径处最小膜厚作为参考膜厚（用符号refh表示），大小为1 μm。而锥度正切定义为

对式（1）进行量纲1处理，得

图2　密封面几何模型Fig.2　Geometric model of sealing interface

图2所示几何模型结构参数与操作工况参数及文献［15］中相关参数分别如表1中Value 1和Value 2［15］所述，其中，本文计算的模拟介质为22#液压油。

表1　R密封面几何结构参数与工况参数Table 1　Sealing interface geometrical parameters and operational parameters

1.2控制方程

为确定密封端面间液膜控制方程及简化数值计算，做如下假设：

（1）液膜厚度为微米级，足够小，适用于雷诺方程；

（2）密封面间流体为牛顿流体，工作状态为稳态层流且黏度不随压力变化；

（3）密封面间由两相混合组成的薄膜分为全液膜区和空穴区，全液膜区流体为不可压缩，空穴区压力保持不变；

（4）密封流体的热楔及配对密封环的热变形忽略不计，且忽略除离心力外的惯性项的影响；

（5）该模型适用于等温绝热工况。

鉴于上述假设，液膜润滑控制方程在极坐标下的表达式［16-17］为

对于机械密封空化，目前主要存在两种空化模型：传统的Reynolds模型和JFO模型，前者仅给出了液膜破裂位置的边界条件，但无法正确描述液膜再形成位置的边界条件，不满足质量守恒定律；而后者不仅给出了液膜破裂位置的边界条件

同时，也给出了液膜再形成位置的边界条件

该模型在数值求解过程中可实现跟踪动态液膜，能很好地满足质量守恒定律。因此本文采用满足质量守恒的JFO空化模型。

在全液膜区，液膜密度cρ保持不变，则式（3）简化为

在空穴区，液膜压力为空化压力cp，满足，则式（3）简化为

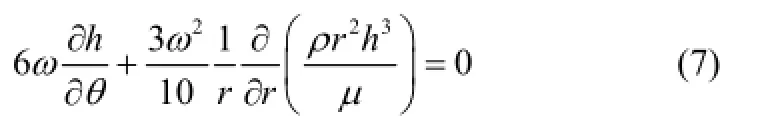
为实现JFO空化模型在数值计算过程中自动捕捉液膜破裂和再形成边界及将全液膜区和空穴区的控制方程统一化，引入通用变量φ和空化数F，两参数满足

具体定义为

全液膜区：

空穴区：

对式（3）进行量纲1化，可得到同时描述全液膜区和空穴区压力分布的通用控制方程式中，量纲1参量为

1.3边界条件设置

图1所示机械密封配对的密封环关于中心对称，数值计算时选取一个波度为计算周期。量纲1化之前式（3）的初始边界条件为

周期性边界条件为）

1.4数值求解方法

1.4.1计算域网格划分图3所示计算域局部网格，图中剖面线为以节点P为中心的控制体积。

图3　极坐标下控制体积示意图Fig.3　Control volume in polar coordinates

为使模拟计算结果更接近于实际，计算域网格划分的数目应遵守随着网格数目的增加计算结果不再有显著变化的原则。因此，在满足网格密度的条件下，应当尽量减少计算量，提高计算收敛的稳定性和收敛速度。由于密封面间液膜中发生空穴的位置及区域未确定，控制体积网格划分采用结构化网格。

1.4.2控制方程离散化为获得迭代代数方程，采用有限控制体积法对控制方程进行离散［20］。首先，在控制体积内对式（11）进行积分，表达式为

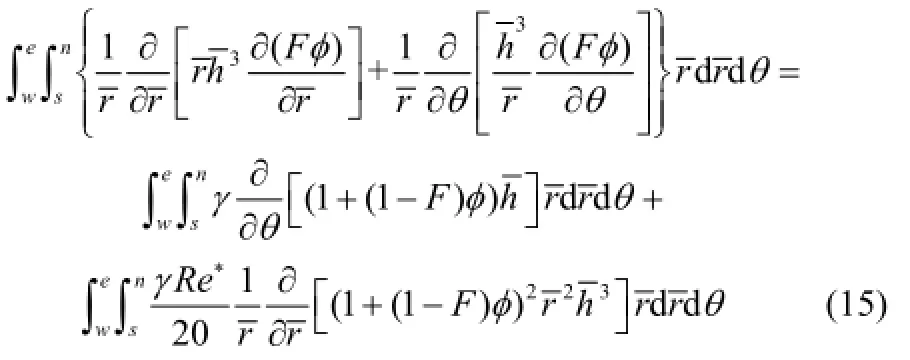
在控制体积中，沿we→，角度为θΔ；沿sn→，距离为rΔ，则式（15）的离散式整理为

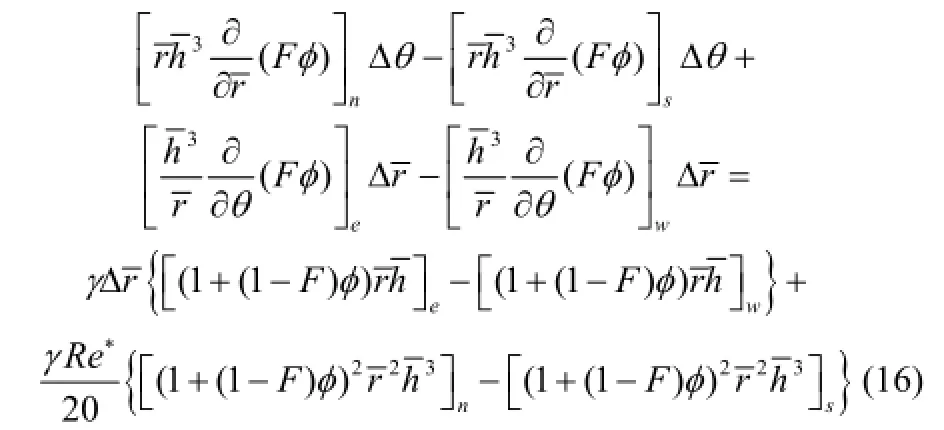
式（16）等号左边的压差流项采用中心差分格式，而等号右边的剪切流项和离心惯性项采用迎风差分格式［21］。则中心节点P处φ值的代数方程表达式如

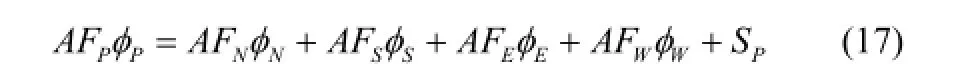
式中，

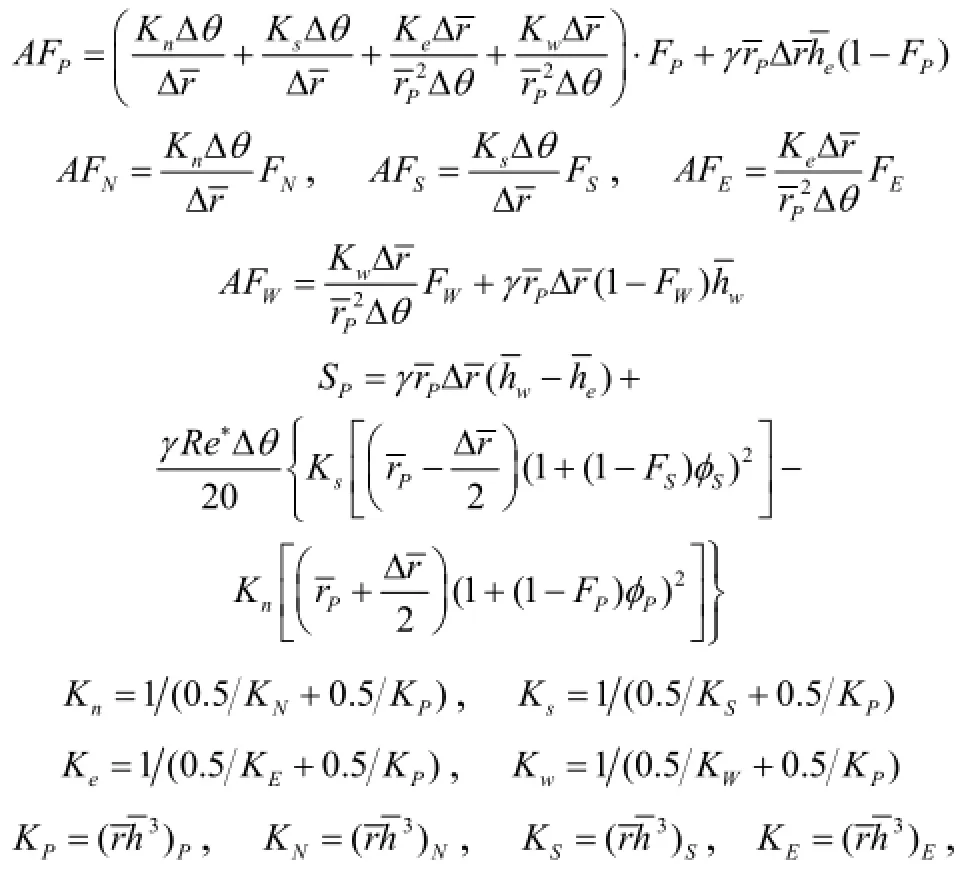
1.4.3代数方程迭代方法式（17）中的PS项含有φ和F的二次项，致使方程具有非线性［22］；因此，在迭代过程中，将φ和F的上一次迭代值代替当前的迭代值。为进一步提高迭代速度并保证良好的收敛性，采用Gauss-Seidel迭代方法进行求解，并引入松弛因子ξ和η，对每一步计算的φ和F进行迭代更新，迭代更新方程为

式中，

代数方程迭代收敛判别准则为

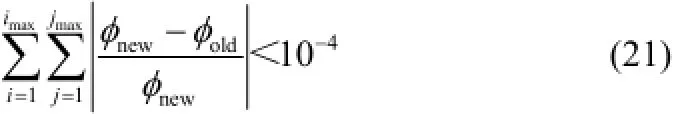
2　计算结果与分析

2.1程序算法验证与算例

以文献［15］中的结构参数和工况参数（表1）为例，采用本文数值计算方法进行计算，将计算得到的半个波度周期内膜压分布（表2）与文献［15］中的膜压分布数据表（表3）进行对比。

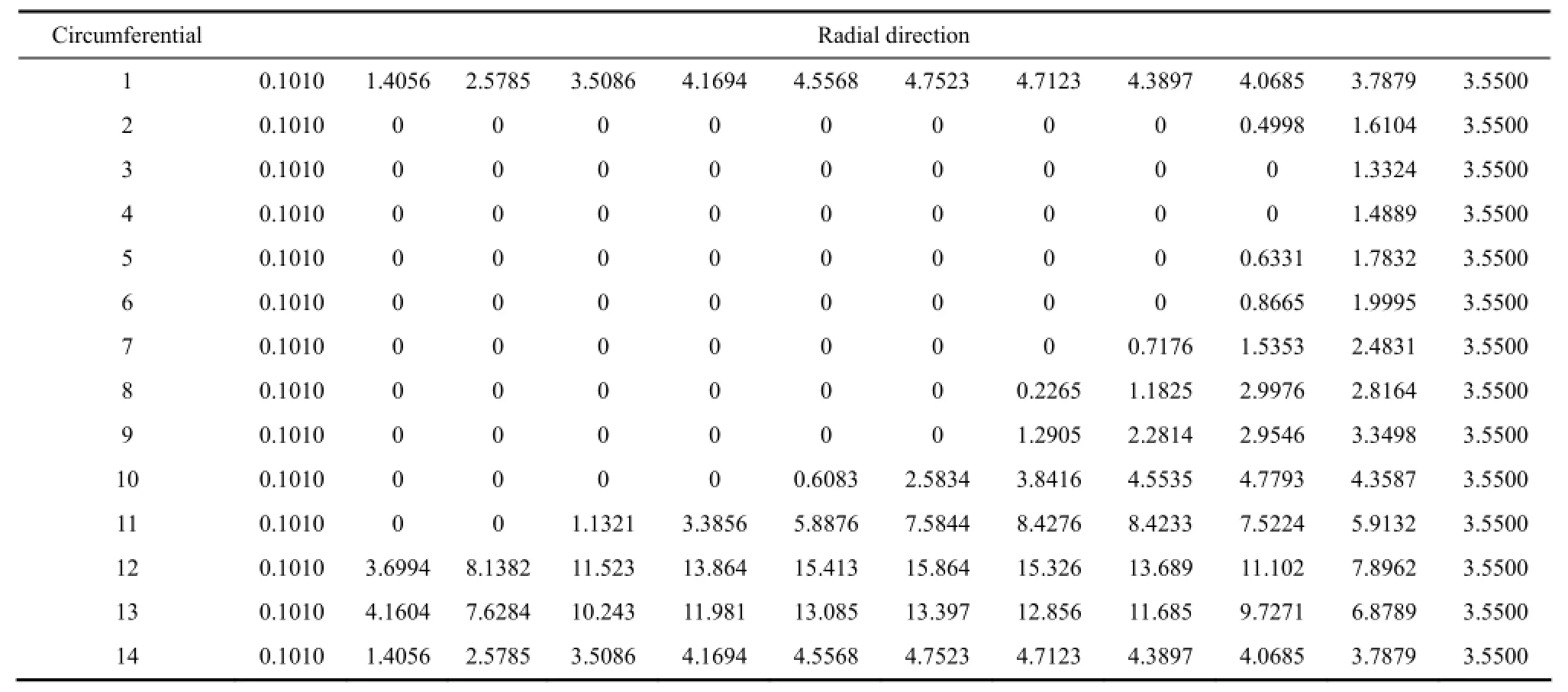
表2　R采用本文数值计算方法求解的计算周期内膜压分布数据Table 2　Film pressure distribution datasheet calculated by this paper's numerical method/MPa

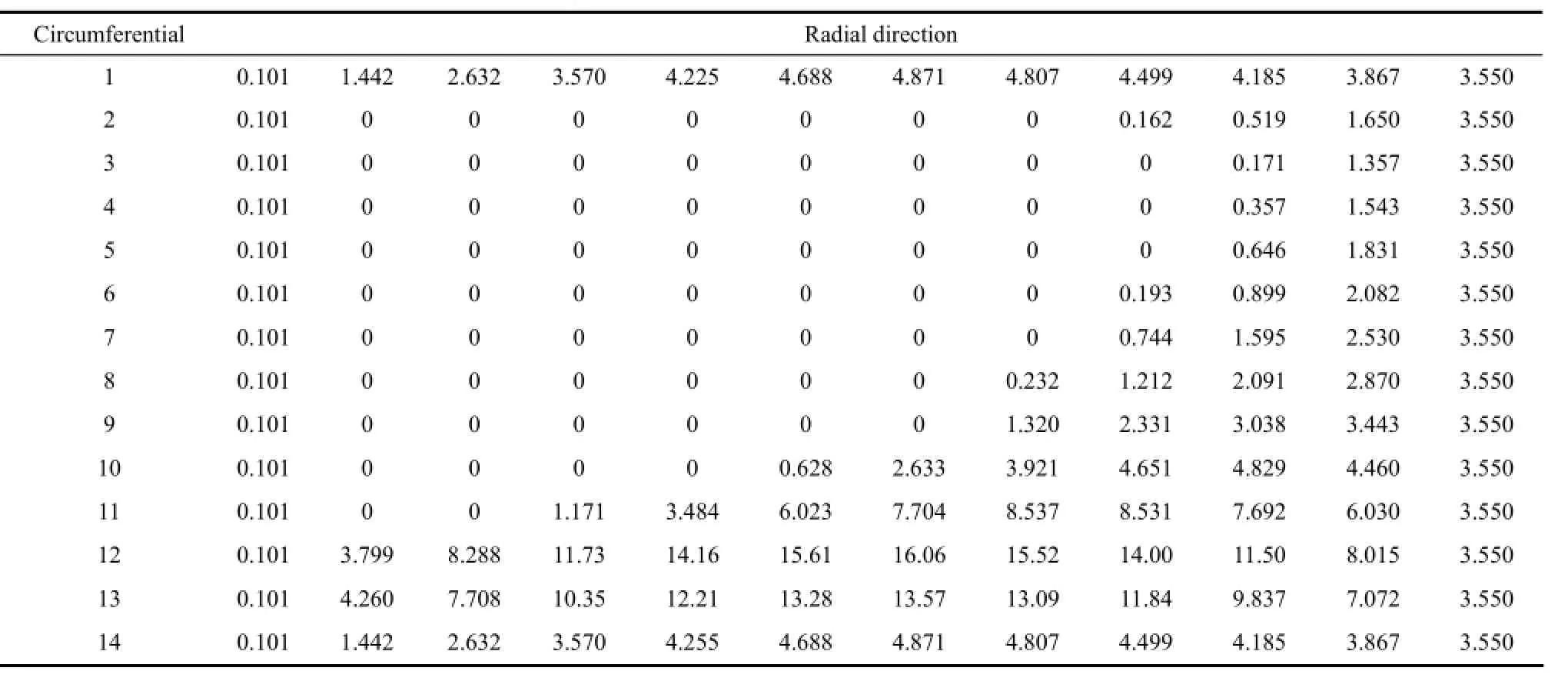
表3　R文献［15］中的膜压分布数据Table 3　Film pressure distribution datasheet of Ref. ［15］/MPa

对比表2和表3可知，采用本文数值计算方法得到的计算域压力值、空化率与文献［15］中的计算结果误差分别为2%～4%、2.3%，空化区域边界沿半径方向向外径侧偏移一个网格距离。由于本文算法精度较高，计算误差在允许范围内，可认为两者计算结果十分吻合，从而证明本文算法的准确性，可很好地开展本文的后续计算。

以表1中的Values 1参数为算例，并根据表4所述的计算域网格无关性检测结果，确定在单周期计算域内沿径向和周向网格划分为50×50，计算得到的单周期内膜压分布如图4所示。

表4　R网格划分数目对液膜空化率的影响Table 4　Effects of grid numbers on liquid film cavitation rate

图4　算例量纲1膜压分布Fig.4　Dimensionless film pressure distribution of example

由图4可知，在液膜收敛区域、发散区域分别形成高压区和低压区。液膜经当前高压区进入低压区后，由于局部压力过低，液膜无法承受致使开始破裂；经低压区后进入下一个计算周期的高压区，随着压力的升高，破裂液膜逐渐聚集再形成，因此在液膜破裂位置和再形成位置的区间形成空穴区，即图4中颜色较深位置。

2.2对空穴初生及区域演变影响

2.2.1波幅的影响波幅是波度尺寸表征参数之一。取量纲1波幅A分别为0.05、0.10、0.65和1.50，量纲1锥度表征量B分别为1和0.4时，量纲1半处沿周向的液膜压力及液膜空穴区分布如图5、图6和图7所示。

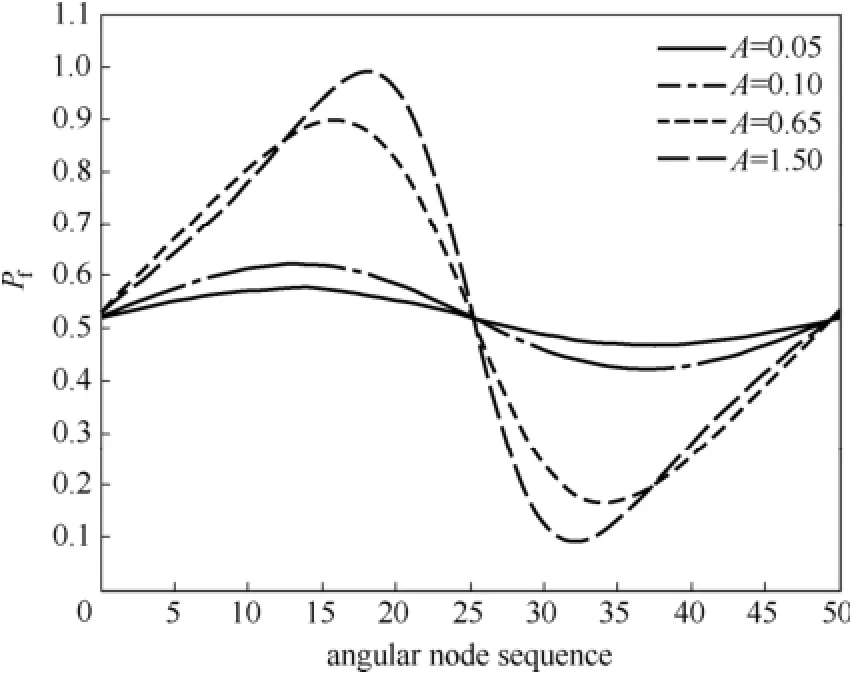
图5　不同A时，B=1、=1.07处的量纲1膜压分布Fig.5　Effects of parameter A on dimensionless film pressure distribution at B=1=1.07

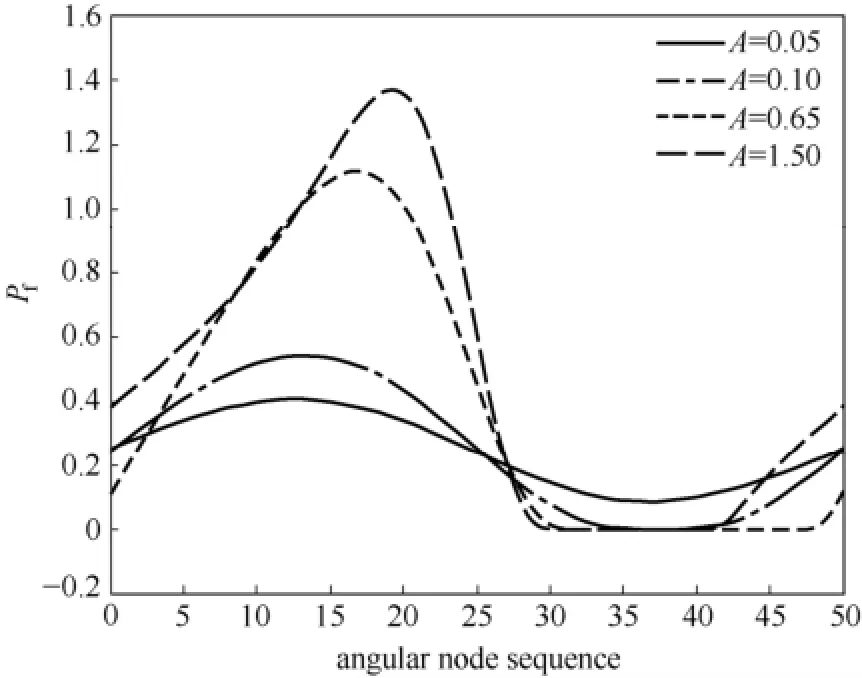
图6　不同A时，B=0.4、=1.07处的量纲1膜压分布Fig.6　Effects of parameter A on dimensionless film pressuredistribution at B=0.4=1.07

由图5可知：不考虑锥度时即B=1，因波度的存在，液膜沿周向收敛间隙产生高压区，沿发散间隙产生低压区。随着波幅的增加，流体动压润滑效应逐渐增强，高压区最高压力显著增加，而低压区最低压力明显降低。当A=1.5时，由于低压区最低压力仍高于空化压力（量纲1空化压力为0），未产生空穴。因此，液膜压力发生显著变化，主要是波度产生流体动压润滑效应作用的结果。

考虑锥度后（量纲1负锥度值为0.6），如图6所示，端面液膜产生流体静压润滑效应，在Sommerfeld无空化边界下，高压区和低压区的最高/最低压力的数值大小相比不考虑锥度时均增加。因采用JFO质量守恒空化边界，当A低于0.05时未产生空穴，增加至0.05～0.1区间的某值时即将发生空化；当A为0.1时低压区局部压力已低于空化压力，产生空穴。

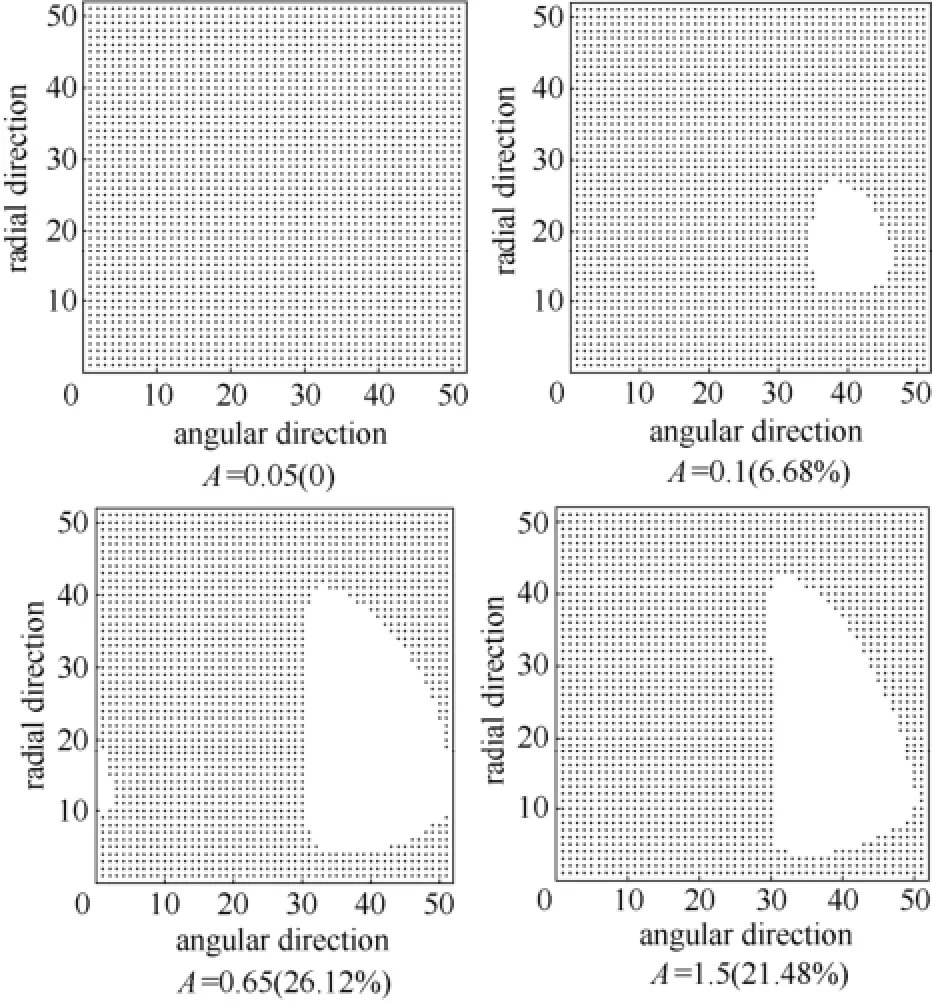
图7　B=0.4、不同A时液膜空穴分布（空白处为空穴区）Fig.7　Effects of parameter A on cavitation region distribution at B=0.4 （the blank is cavitation region）

随着波幅的增加，流体动压润滑效应逐渐增强，空穴边界沿径向向两侧扩展，而沿周向单侧扩展，空化区域增大，如图7所示。当A达到0.65时，空化率达到最大值；继续增大至1.5，液膜破裂位置几乎不变，位于周向第31个节点所在半径线上；但因流体动压润滑效应的减弱，空化区域缓慢降低，液膜再形成位置沿周向向破裂位置收缩。

2.2.2波数的影响波数也是波度尺寸表征参数之一。取波数K分别为4、12、24和48，量纲1波幅A和量纲1锥度表征量B分别为0.7和0.4时，量纲1半径=1.07处沿周向的液膜压力及液膜空穴区分布如图8和图9所示。

由8图可知：高压区最高压力基本位于同一位置未发生偏移，在Sommerfeld无空化边界下，低压区最低压力分布位置相类似。因采用JFO质量守恒空化边界，当K=4时，低压区已初生空穴。

随着波数的增加，流体动压润滑效应增强，液膜破裂位置形成所谓“负压”的能力也随之增强。由图9可知，液膜开始破裂位置基本不变且沿周向第31个节点所在半径方向向两侧延伸，液膜再形成位置沿着周向单侧外移，空化区域虽逐渐扩大，但形状基本保持不变。当K达到24时，液膜空化率最大；随着波数的进一步增加，流体动压润滑效应非增却降，致使空化率降低；当波数增加一倍即K=48时，空化区域降低约2.5%，变化较小；但空化区域形状呈现狭长变化趋势。

图8　不同K时，A=0.7、B=0.4、=1.07处的膜压分布Fig.8　Effects of parameter K on dimensionless film pressure distribution at A=0.7， B=0.4，=1.07

图9　A=0.7、B=0.4、不同K时液膜空穴分布Fig.9　Effects of parameter K on cavitation region distribution at A=0.7， B=0.4 （the blank is cavitation region）

2.2.3锥度的影响取量纲1锥度表征量B分别为0.20、0.55、0.75和1.10，量纲1波度A分别为0和0.7时，量纲1半径=1.07处沿周向的液膜压力及液膜空穴区分布如图10、图11和图12所示。

由图10可知，不考虑波度、量纲1锥度为负锥度时，密封面间隙沿径向发散，进入间隙内的液体在最小膜厚处发生节流膨胀，压力急剧降低，液膜压力呈凹形抛物线变化；量纲1锥度为正锥度时，密封面间隙沿径向收敛，进入间隙的液体受阻，压力缓慢降低，液膜压力呈凸形抛物线变化。当锥度由负锥度增加至正锥度，液膜压力由凹抛物线渐变至凸抛物线，主要是流体静压润滑效应作用的结果。

图10　不同B时，A=0、=1.07处的量纲1膜压分布Fig.10　Effects of parameter B on dimensionless film pressure distribution at A=0，=1.07

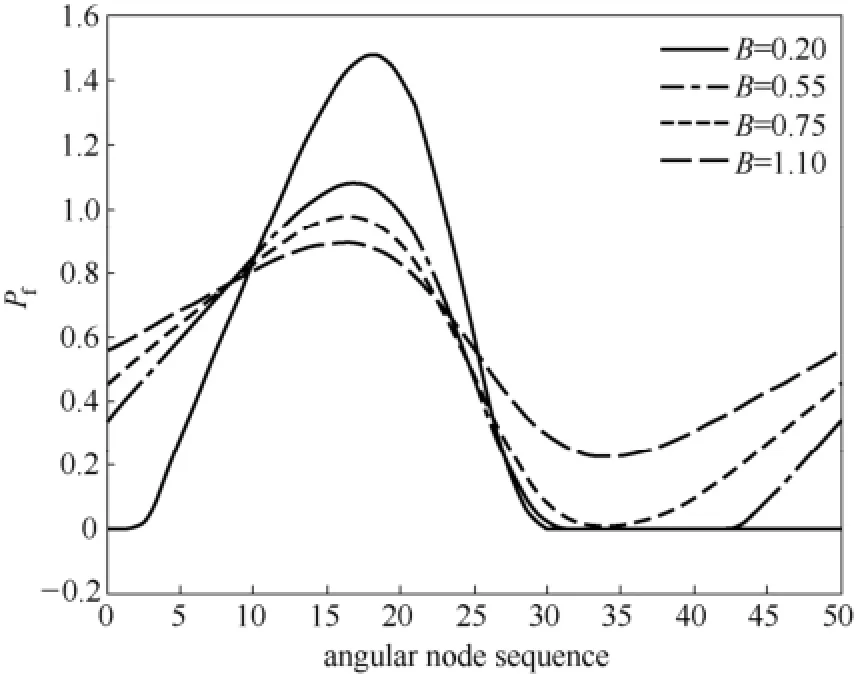
图11　不同B时，A=0.7、=1.07处量纲1膜压分布Fig.11　Effects of parameter B on dimensionless film pressure distribution at A=0.7=1.07

考虑波度后，随着锥度由负锥度向正锥度增加，逐渐增强的流体静压润滑效应较波度产生的流体动压润滑效应占主导作用，促进低压区压力呈增大趋势，液膜破裂位置形成所谓“负压”的能力却随之减弱，空化区域逐渐较小。同样，在空化区域演化过程中，其形状基本保持不变。

2.3对空化率影响

绘制密封面间隙液膜中空化区域所占的比率即空化率随周向波度和径向锥度的变化曲线，分别如图13、图14及图15所示。

图12　不同B时液膜空穴分布Fig.12　Effects of parameter B on cavitation region distribution（the blank is cavitation region）

图13　A=0～2， 不同B时空化率的变化Fig.13　Cavitation rate variation at A=0—2 and different B

由图13和图14可知：当量纲1波幅A为低波幅0～0.5，量纲1锥度（B-1）＜0时，空化率迅速增加，尤其是（B-1）≤-0.5时，显著促进了空穴的初生及空化区域演变；当量纲1锥度趋向于正锥度时，空化率明显降低至零，进而抑制了空化的初生及空化区域演变。当A＞0.5后，空化率呈缓慢下降趋势。

由图15可知：当量纲1波幅A为低波幅0～0.5，波数为高频波即K≥8时，空化率迅速增加，亦显著促进了空穴的初生及空化区域演变；当波数为低频波即K＜8，尤其是K=4时，未发生空化，有效抑制了空穴的初生及空化区域演变。

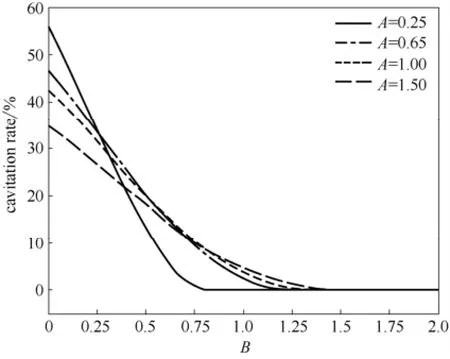
图14　B=0～2， 不同A时空化率的变化Fig.14　Cavitation rate variation at B=0—2 and different A

图15　A=0～2，不同K时空化率的变化Fig.15　Cavitation rate variation at A=0—2 and different K

3　结　论

（1）通过与文献［15］计算结果对比，两者十分吻合，本文采用有限控制体积法离散统一描述全液膜区和空穴区压力分布的通用控制方程的方法是可行的。

（2）液膜润滑机械密封端面空穴初生及空化区域演变是密封面微观波度和锥度共同作用的结果，而空穴初生即液膜开始破裂位置位于膜厚沿周向发散的低压区，且在空化区域演变时其沿某一半径方向保持不变，空化区域形状亦基本保持不变。

（3）在低波幅、高频波数或负锥度较大时，液膜空化率迅速增加，促进了空化发生；在低波幅、低频波数或锥度由负锥度趋向于正锥度时，液膜空化率明显降低甚至降为零，有效抑制了空化发生。

（4）本文考虑了端面微观波度和锥度对空穴初生及其演变等影响，但未提及微观粗糙度和角偏差等各因素影响；因此，后续将进一步开展相关研究。

符号说明

A——量纲1波度波幅

Am——波度波幅，m

B——量纲1锥度表征量

F——空化数

h——密封面间隙总膜厚，m

href——参考膜厚，m

hid，min——密封面内径处最小膜厚，m

hod，min——密封面外经处最小膜厚，m

K——波度波数

Pf——量纲1液膜压力

p——密封面间隙液膜压力

pi——密封面内径处压力，Pa

po——密封面外径处压力，Pa

pc——空化压力，Pa

Re∗——密封面间隙流体Reynolds数

R——量纲1外半径

r——密封面半径，m

ri——密封面内半径，m

ro——密封面外半径，m

Vn——外法线方向速度，m·s-1

α——密封面锥度，rad

φ——量纲1通用变量

γ——密封面间隙流体过程系数

η——空化数迭代松弛因子

μ——密封面间隙流体动力黏度，Pa·s

θ——密封面圆周弧度，rad

θi——单周期波度初始弧度，rad

ρ——空化区气液混相平均密度，kg·m-3

ρc——密封面间隙流体密度，kg·m-3

ω——密封面旋转角速度，rad·s-1

ξ——量纲1压力迭代松弛因子

下角标

E——控制容积东侧相邻节点

e——控制容积东侧边界

i——密封面圆周方向网格节点下标

imax——密封面圆周方向网格节点总数

j——密封面半径方向网格节点下标

jmax——密封面半径方向网格节点总数

N——控制容积北侧相邻节点

n——控制容积北侧边界

new ——当前迭代过程变量值

old ——上一次迭代过程变量值

P ——控制容积中心节点

S ——控制容积南侧相邻节点

s ——控制容积南侧边界

W ——控制容积西侧相邻节点

w ——控制容积西侧边界

References

［1］ 王涛， 黄伟峰， 王玉明. 机械密封液膜汽化问题研究现状及进展［J］. 化工学报， 2012， 63 （11）： 3375-3382. DOI： 10.3969/j.issn.0438-1157.2012.11.001. WANG T， HUANG W F， WANG Y M. Research and progress of mechanical seals operating with vaporization transition ［J］. CIESC Journal， 2012， 63 （11）： 3375-3382. DOI： 10.3969/j.issn.0438-1157.2012.11.001.

［2］陈汇龙， 吴强波， 左木子， 等. 机械密封端面液膜空化的研究进展［J］. 排灌机械工程学报， 2015， 33 （2）： 138-144. DOI： 10.3969/ j.issn.1674-8530.14.0085. CHEN H L， WU Q B， ZUO M Z， et al. Overview on liquid film cavitation in mechanical seal faces ［J］. Journal of Drainage and Irrigation Machinery Engineering， 2015， 33 （2）： 138-144. DOI：10.3969/j.issn.1674-8530.14.0085.

［3］唐飞翔， 孟祥凯， 李纪云， 等. 基于质量守恒的Laserface液体润滑机械密封数值分析 ［J］. 化工学报， 2013， 64 （10）： 3694-3700. DOI： 10.3969/j.issn.0438-1157.2013.10.029. TANG F X， MENG X K， LI J Y， et al. Numerical analysis of Laser-Face liquid mechanical seal based on mass conservation ［J］. CIESC Journal， 2013， 64 （10）： 3694-3700. DOI： 10.3969/j.issn.0438-1157.2013.10.029.

［4］FINDLAY J A. Cavitation in mechanical face seals ［J］. Journal of Lubrication Technology， 1968， 90 （2）： 356-364.

［5］NAU B S. Observations and analysis of mechanical seal film characteristics ［J］. Journal of Lubrication Technology. 1980， 102 （3）：341-347.

［6］QIU Y， KHONSARI M M. On the prediction of cavitation in dimples using a mass-conservative algorithm ［J］. Journal of Tribology， 2009，131 （4）： 41702-41711.

［7］QIU Y， KHONSARI M M. Experimental investigation of tribological performance of laser textured stainless steel rings ［J］. Tribology International， 2011， 44 （5）： 635-644.

［8］孟凡明， 王战江. 微造型表面上气穴发生机理初步研究 ［J］. 摩擦学学报， 2011， 31 （2）： 137-143. DOI： 10.16078/j.tribology.2011.02.014. MENG F M， WANG Z J. Preliminary study on mechanism for occurrence of cavitation on a textured surface ［J］. Tribology， 2011， 31（2）： 137-143. DOI： 10.16078/j.tribology.2011.02.014.

［9］DOWSON D， TAYLOR C M. Cavitation in bearings， annual reviews［J］. Fluid Mechanics， 1979， （11）： 35-66.

［10］JAKOBSSON B， FLOBERG L. The finite journal bearing，considering vaporization ［J］. Wear， 1958， 2 （2）： 85-88.

［11］OLSSON K O. Cavitation in dynamically loaded bearings ［J］. Wear，1967， 55 （2）： 295-304.

［12］ 胡纪滨， 刘丁华， 魏超. 径向直线槽端面密封空化特性数值模拟 ［J］.摩擦学学报， 2011， 31 （6）： 551-556. DOI： 10.16078/j.tribology.2011.06.007. HU J B， LIU D H， WEI C. Numerical simulation for cavitation of groove face seals ［J］. Tribology， 2011， 31 （6）： 551-556. DOI：10.16078/j.tribology.2011.06.007.

［13］郝木明， 庄媛， 章大海， 等. 考虑空化效应的螺旋槽液膜密封特性数值研究 ［J］. 中国石油大学学报 （自然科学版）， 2015， 39 （3）：132-137 . DOI： 10.3969/j.issn.1673-5005.2015.03.018. HAO M M， ZHUANG Y， ZHANG D H， et al. Numerical study on sealing performance of spiral groove liquid film seal considering effects of cavitation ［J］. Journal of China University of Petroleum（Natural Science）， 2015， 39 （3）： 132-137. DOI： 10.3969/j.issn.1673-5005.2015.03.018.

［14］LUBBINGE H. On the lubrication of mechanical face seals ［D］. Enschede： University of Twente， 1999.

［15］顾永泉. 机械密封的空化和空化边界确定 ［J］. 流体机械， 1998， 26（12）： 16-20. GU Y Q. Determination of cavitation and cavitation boundary of mechanical seal ［J］. Fluid Machinery， 1998， 26 （12）： 16-20.

［16］PINKUS O， LUND J W. Centrifugal effects in thrust bearings and seals under laminar conditions ［J］. Transactions of the ASME， 1981，103： 126-136.

［17］YU T H， SADEGHI F. Groove effects on thrust washer lubrication ［J］. Journal of Tribology， 2001， 123 （2）： 295-304.

［18］ 李强， 郑水英， 刘淑莲. 计入JFO边界条件的滑动轴承性能分析［J］. 机械强度， 2010， 32 （2）： 270-274. LI Q， ZHENG S Y， LIU S L. Analysis of the performance of journal bearings with JFO boundary condition ［J］. Journal of Mechanical Strength， 2010， 32 （2）： 270-274.

［19］PAYVAR P， SALANT R F. A computational method for cavitation in a wavy mechanical seal ［J］. Journal of Tribology， 1992， 114： 199-204.

［20］PATANKAR S V. Numerical Heat Transfer and Fluid Flow ［M］. London： Taylor & Francis， 1980： 72-73.

［21］XIONG S W， WANG J Q. Steady-state hydrodynamic lubrication modeled with the Payvar-Salant mass conservation model ［J］. Journal of Tribology， 2012， 134： 031703-1-031703-16.

［22］赵一民， 苑士华， 胡纪滨， 等. 基于质量守恒边界条件的螺旋槽旋转密封性能分析 ［J］. 机械工程学报， 2014， 50 （22）： 142-149. DOI：10.3901/JME.2014.22.142. ZHAO Y M， YUAN S H， HU J B， et al. Performance analysis of spiral-groove rotary seals considering mass conserving boundary condition ［J］. Journal of Mechanical Engineering， 2014， 50 （22）：142-149. DOI： 10.3901/JME.2014.22.142.

Effects of waviness and taper on cavitation characteristics of liquid lubricated mechanical seals

LI Zhentao， HAO Muming， YANG Wenjing， HAN Jie， REN Baojie
（Institute of Sealing Technology， China University of Petroleum， Qingdao 266580， Shandong， China）

In order to further probe into the influence factors of cavitation start and evolution， the mathematical model of liquid film lubricated mechanical seals considering the micro circumferential waviness and radial taper was established based on the mass-conservative cavitation model. Liquid film governing equation was discretized by the finite control volume method and was solved by the Gauss-Seidel relaxation iterative algorithm. The effects of different waviness amplitudes， waviness numbers and tapers on the cavitation characteristics were analyzed. The results indicated that the start and evolution of the cavitation were affacted by the combined action of the hydrodynamic lubrication effect produced by the circumferential waviness and the hydrostatic lubrication effect which was greatly influenced by radial taper. To a large extent， changing of the cavitation area along the circumferential direction was influenced by the waviness， while that along the radial direction depended on the taper. The rupture position of liquid was located where film thickness diverged in the depression region at the start stage of cavitation， while the subsequent rupture direction remained unchanged at the evolution stage of cavitation. The cavitation rate was dramatically accelerated at the situations of dimensionless waviness amplitude not beyond 0.5 and waviness number greater than or equal 8， or dimensionless negative taper value greater than 0.5， which promoted the occurrence of cavitation. But under the same waviness amplitude and waviness number less than 8or the taper tending to be positive， the cavitation rate was retarded， which effectively inhibited the occurrence of cavitation.

date： 2015-11-18.

Prof. HAO Muming， haomm@upc.edu.cn

supported by the National Natural Science Foundation of China （51375497）， and the Shandong Special Projects of Independent Innovation and Achievement Transformation （2014ZZCX10102-4）..

mechanical seals； liquid lubricated； waviness； taper； cavitation； finite control volume method

TH 117.2

A

0438—1157（2016）05—2005—10

2015-11-18收到初稿，2016-01-29收到修改稿。

联系人：郝木明。第一作者：李振涛（1983—），男，博士研究生。

国家自然科学基金项目（51375497）；山东省自主创新及成果转化专项（2014ZZCX10102-4）。