易腐商品需求同时依赖库存量与延期支付期限的库存策略及模型

崔 玲 ，彭 凯 ，胡劲松，Vladimir V.Mazalov

（青岛大学1a.经济学院；1b.管理科学与工程系，山东 青岛 266071；2.山东科瑞石油装备有限公司，山东 东营 257067；3.俄罗斯科学院 卡列里科学中心 应用数学研究所）

传统库存模型研究了“一手交钱一手交货”的市场交易规则下最优批量订购问题。随着经济的发展，市场竞争日趋激烈，许多供应商提供延期支付策略以提高自身竞争力，零售商也提供延期支付策略以刺激市场需求，即大部分市场交易不再遵循“一手交钱一手交货”的市场交易规则。Goyal［1］首次提出了允许延期支付的EOQ 模型，研究了供应商为零售商提供延期支付策略的单级延期支付下零售商最优库存策略问题。随后，众多学者进行了拓展研究。文献［2］中将Goyal的模型扩展到易腐商品的情形，文献［3］中研究了部分延期支付的批量订购策略问题。考虑到供应商为零售商提供延期支付策略的同时，零售商也为消费者提供延期支付策略，文献［4-5］中研究了两级延期支付下库存策略问题。

上述文献均假设市场需求为常数或仅依赖于销售价格。但现实中，市场需求受到多种因素的影响，如服务、广告等。考虑到延期支付可以刺激需求，文献［6-7］中研究了市场需求依赖延期支付期限的两级延期支付库存策略问题。观察到展销商品大量堆积更容易吸引消费者的注意，从而创造更多的市场需求，文献［8-9］中研究了需求依赖零售商库存量的两级延期支付批量订购问题。

针对延期支付问题，国内学者也展开了大量研究。周永务［10］揭示了延期支付对库存系统最优订货策略的影响。潘义前等［11］考虑了易变质商品的延期支付库存模型。文献［12-13］中研究了延期支付下供应链库存协调问题。然而，目前绝大部分国内文献尚未考虑库存量以及延期支付期限对商品需求的影响。

与现有文献不同，本文研究了更一般的延期支付库存策略问题：①市场需求同时依赖于零售商延期支付策略以及库存量；②考虑了商品的易腐特性；③研究了供应商与零售商同时提供延期支付策略的两级延期支付策略问题；④放宽了两级延期支付库存模型中供应商允许的延期支付期限要长于零售商允许的延期支付期限的假设条件。本研究更加贴近现实，可以为零售商企业订购决策以及营销决策提供理论参考。例如超市等零售企业，可以参考本研究内容，选择展销商品以发挥展销柜台的更大作用。

1 模型建立

1.1 符号说明

k—订购一次的固定费用

c—商品单位进价

s—商品单位售价

h—商品单位持有成本（不包括利息支付）

θ— 商品变质率，0＜θ＜1

Ie—零售商单位货币单位时间利息收益

Ip—零售商单位货币单位时间利息支付

M—供应商为零售商提供的延期支付期限

N—零售商为顾客提供的延期支付期限

T—订货周期（决策变量）

Q—每次订货量

AR—零售商平均利润

I（t）— 零售商t时刻库存量，0＜t＜T

1.2 模型假设

（1）零售商以价格c从供应商处订货，并以价格s销售给顾客。

（2）不允许缺货。

（3）补货瞬时完成，不考虑提前期。

（4）零售商收到订购货物的同时，商品开始变质，变质率为常数θ。

（5）供应商允许零售商期限为M的延期支付，零售商允许顾客期限为N的延期支付。

（6）零售商在时刻t=M时将订货货款支付给供应商；在时刻t=M之前，零售商积累销售收入获得利息收益；在时刻t=M之后，零售商对于尚未销售的商品量及已经销售但尚未获得消费者支付的商品量支付利息成本。

（7）顾客商品需求量同时依赖于零售商商品库存量与延期支付期限

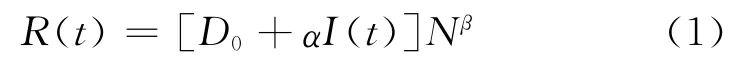
式中，D0，α，β＞0为常数。

1.3 模型刻画

由上述假设可知，零售商库存变化量满足如下微分方程：

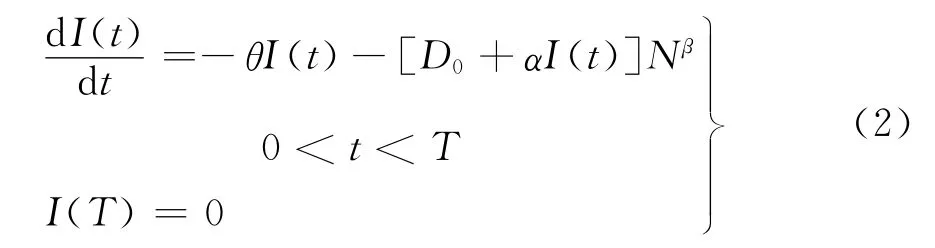
对式（2）求解，易得

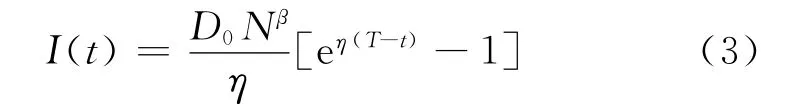
式中，η=θ+αNβ。

由Q=I（0），可得

零售商单周期利润由以下组成：

（1）固定费用C0=k。

（2）商品订购成本

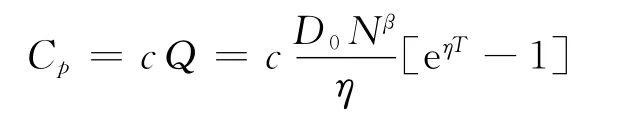
（3）商品持有成本

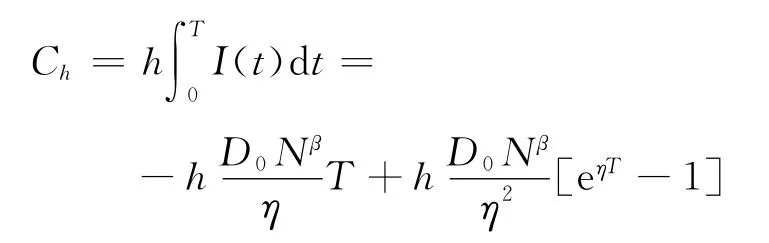
（4）销售收入

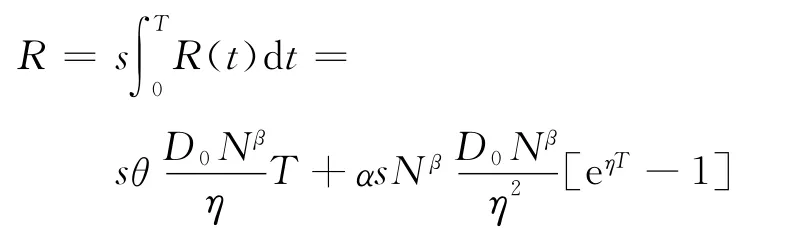
（5）利息支付与利息收益。

根据参数T、M、N的不同值，分为3 种情形讨论：

（1）0≤T+N≤M。零售商在时刻t=M时将订货货款支付给供应商，此时商品已全部售出且销售收入已全部收回，从而零售商无利息支付，仅积累销售收入获得利息收益。

利息支付IP1=0。利息收益

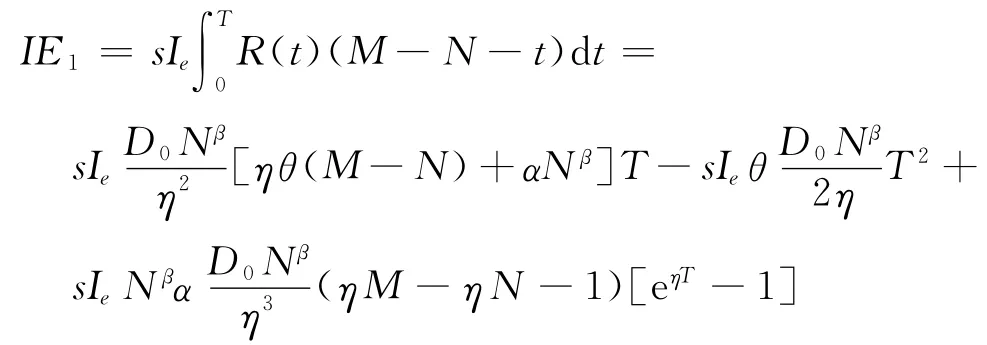
（2）N≤M≤T+N。零售商在时刻t=M时将订货货款支付给供应商，而零售商于时刻t=N时开始获得消费者支付，并于时刻t=T+N时结束。在时间段［M，T+N］，零售商对于尚未销售以及已经销售但尚未获得消费者支付的商品支付利息成本；在时间段［N，M］，零售商积累销售收入获得利息收益。

利息支付与利息收益分别为：

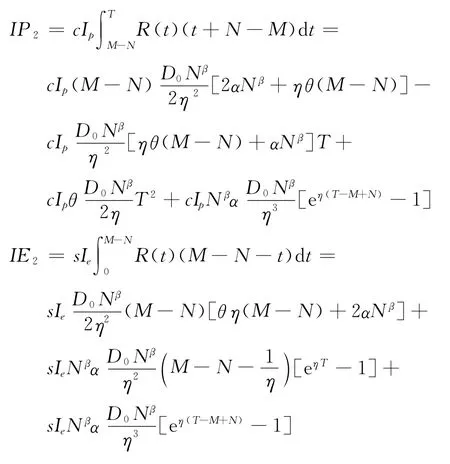
（3）M≤N。零售商在时刻t=M时将订货货款支付给供应商，此刻零售商尚未获得消费者支付，因而零售商无法积累销售收入获得利息收益，但须为全部商品支付利息成本。

利息支付

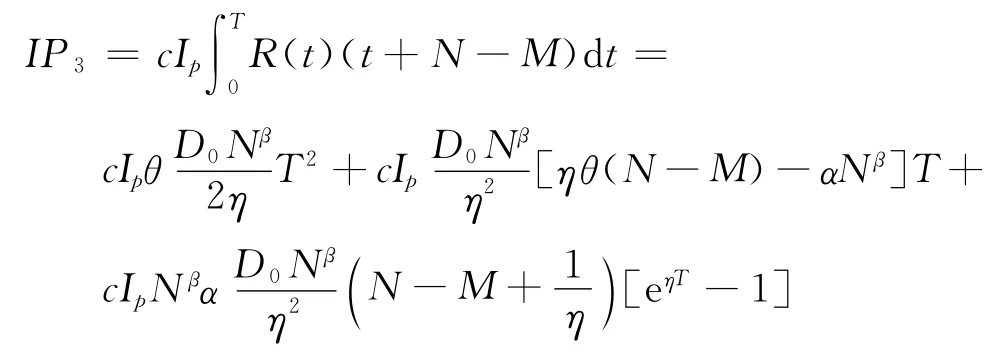
利息收益IE3=0。

综上所述，零售商平均利润为

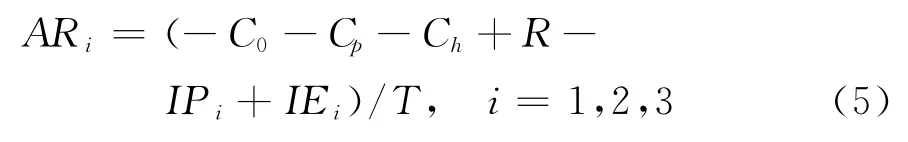
由此，需求同时依赖库存量与延期支付期限的EOQ 模型数学刻画，即

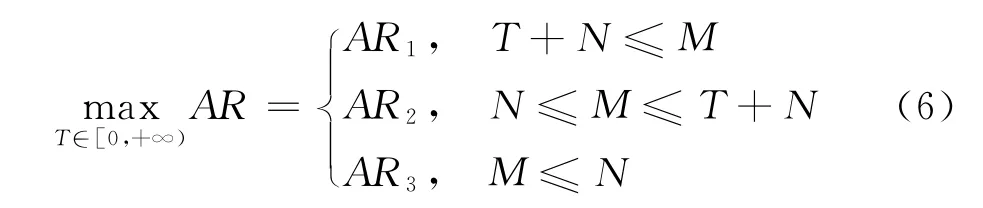
式中，AR i，i=1，2，3由式（5）给定。

2 模型求解

为获得模型式（6）的最优解，首先对AR i，i=1，2，3分别进行讨论。

2.1 AR1（0＜T+N≤M）的最优解

将C0、Cp、Ch、R、IP1、IE1代入式（5），化简可得

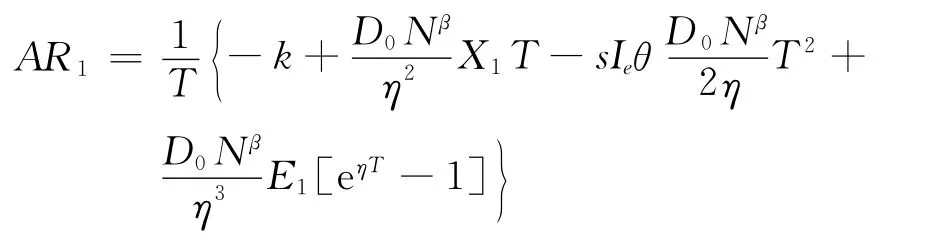
其中：

AR1对T求导，可得

构造辅助函数

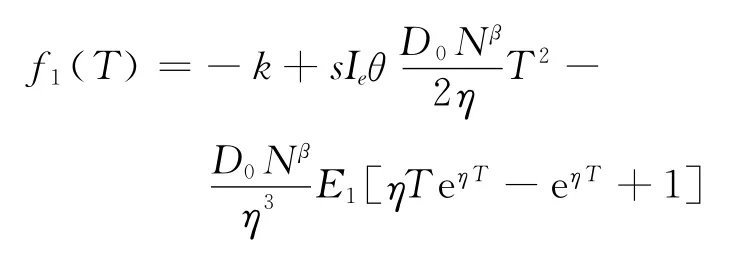
则有

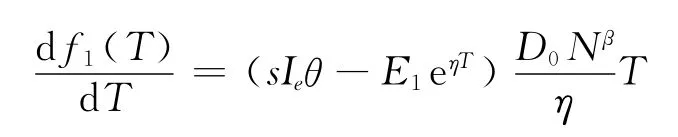
引理1

（1）E1≤0且f1（M-N）≤0，或E1≥0且T#1＜0；或E1≥0，0 ≤T#1≤M-N且f1（T#1）≤0；或E1≥0，T#1＞M-N且f1（MN）≤0时，T*=M-N。

（2）E1≤0且f1（M-N）＞0时，T*=T11。

（3）E1≥0，0≤T#1≤M-N，f1（T#1）＞0且f1（M-N）≥0时，T*=T12。

（4）E1≥0，0≤T#1≤M-N，f1（T#1）＞0且f1（M-N）＜0时，

（5）E1≥0，T#1＞M-N且f1（M-N）＞0时，T*=T15。

其中，

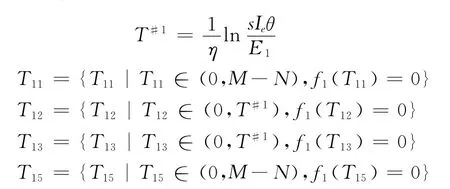
证明详见附录。

由引理1易得0＜T+N≤M时的最优定货周期，记为。

2.2 AR2（N＜M≤T+N）的最优解

将C0、Cp、Ch、R、IP2、IE2代入式（5），化简可得

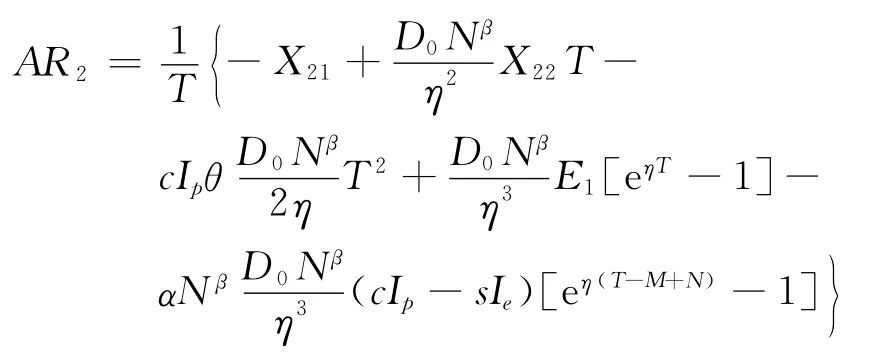
其中：

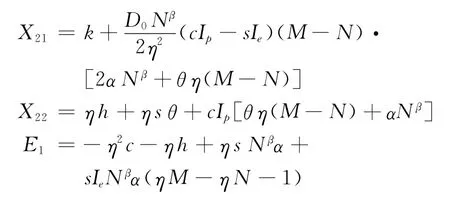
AR2对T求导，得

构造辅助函数

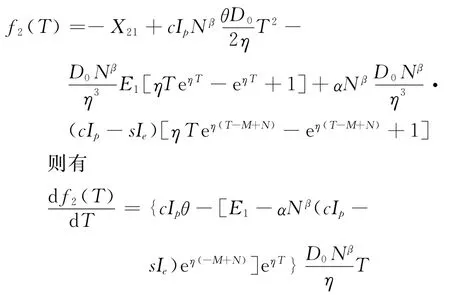
引理2

且f2（T）|T→+∞≥0；或

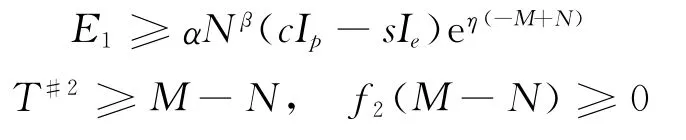
且f2（T）|T→+∞≥0时，T*=M-N。

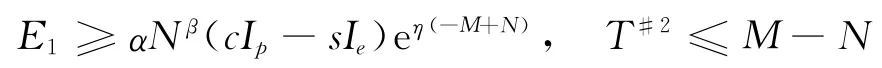
且f2（M-N）＜0；或

且f2（T#2）≤0时，T*=+∞。

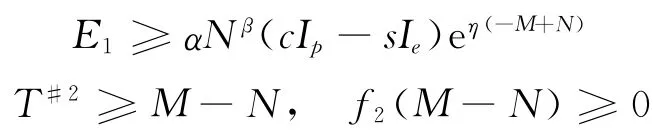
且f2（T）|T→+∞＜0时，

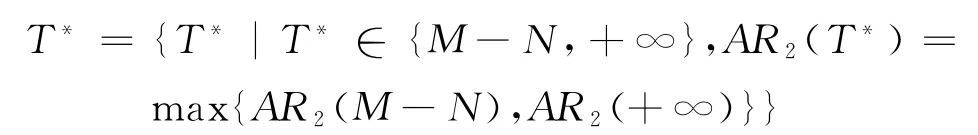
其中：

证明详见附录。

由引理2易得N＜M≤T+N时的最优订货周期，记为。

2.3 AR3（M≤N）的最优解

将C0、Cp、Ch、R、IP3、IE3代入式（5），化简可得

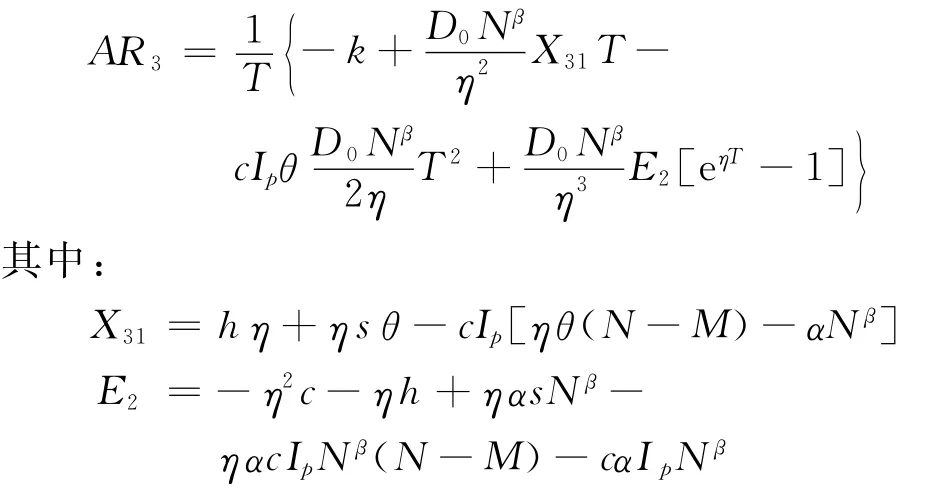
AR3对T求导，得

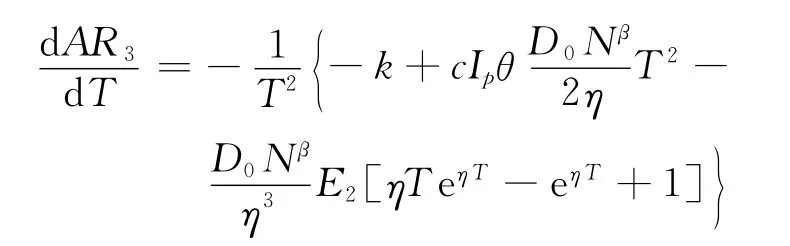
构造辅助函数

引理3

（1）E2≤0且f3（T）|T→+∞≤0，或E2≥0且T#3≤0；或E2≥0，T#3＞0且f3（T#3）≤0时，T*=+∞。

（2）E2≤0且f3（T）|T→+∞＞0时，T*=T31。

（3）E2≥0，T#3＞0，f3（T#3）＞0且f3（T）|T→+∞≥0时，T*=T32。

（4）E2≥0，T#3＞0，f3（T#3）＞0且f3（T）|T→+∞＜0时，

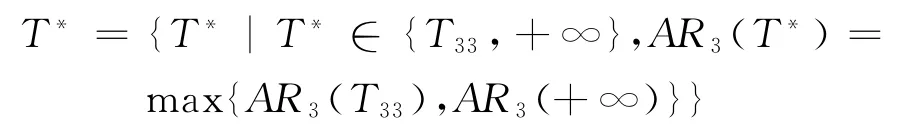
其中：

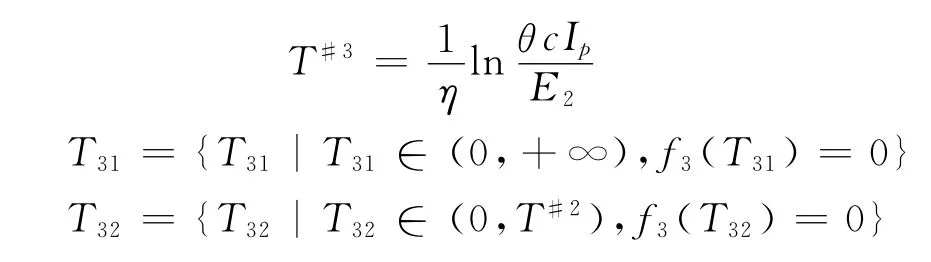
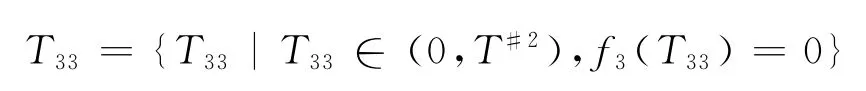
证明详见附录。

由引理3易得M≤N时的最优订货周期，记为。

综上所述，由引理1～3易得如下定理。

定理需求同时依赖库存量与延期支付期限的EOQ 的最优订货周期。

（1）M≥N时，

（2）M≤N时，T*=。

3 算例分析

本节基本参数取值：D0=200，α=0.3，β=0.5，θ=0.1，k=50，h=5，c=10，Ie=0.13，I p=0.15，M=5，N=3，s=20。

表1 给 出 了 参 数α、β、θ、k、M、N、Ie的 灵 敏 度分析。由表可见：

（1）α增加，T*、Q*、AR*均增加。这表明，消费者需求更敏感于零售商库存量时，零售商将增加订购量以刺激需求，并且此时零售商利润增加。

（2）β增加，T*、Q*、AR*均增加。这是因为零售商提供的延期支付期限相同时，消费者需求越依赖于延期支付期限，商品需求量越大，零售商将订购更多产品以满足市场需求，增加利润。

（3）θ升高，T*、Q*、AR*均降低。这表明，变质率升高时，零售商将减少订购量以降低损失，但利润降低。

（4）k升高，T*、Q*增加，AR*降低。这意味着固定费用升高时，零售商增加订购量、延长订货周期以减少订货次数。

（5）M增 加，T*、Q*、AR*均 增 加。这 表 明，供应商延长延期支付期限将刺激零售商订购量，并降低零售商的利息成本，从而导致零售商利润增加。

（6）N增加，T*、Q*、AR*均先升后降。这是因为零售商延长消费者延期支付期限，刺激了消费者需求，增加了零售商收益，但同时增加零售商的利息支付成本，最终表现为利润先增后降。

（7）Ie增加，T*、Q*、AR*均增加。这意味着零售商单位利息收益增加时，零售商增加订购量，刺激消费者需求，提高销售收入，从而积累销售收入获得更高收益，并且最终获得更高利润。

表1 参数α、β、θ、k、M、N、Ie 灵敏度分析

4 结语

本文构建了需求同时依赖于库存量与延期支付期限的经济订购批量模型，考虑了商品的易腐性，给出了零售商利润最大化模型，分析了零售商利润函数的函数性质，并得出最优性条件。利用数值算例，对关键参数进行了灵敏度分析。本文主要贡献：①观察到展销商品的堆积可以创造市场需求，考虑到延期支付也可以刺激市场需求，构造了顾客商品需求量同时依赖于零售商商品库存量以及零售商允许的延期支付期限的顾客商品需求函数；②根据零售商订货周期、供应商允许的延期支付期限、零售商允许的延期支付期限三者的大小关系，分3种情况，建立了零售商平均利润函数，给出了需求同时依赖于库存量与延期支付期限的经济订购批量模型；③对经济订购批量模型进行了求解，给出零售商最优订购周期的解析解。

附录

引理1 略

证明

（1）E1≤0，易知f1（T）在区间［0，M-N］单调递增。又f1（0）=-k＜0，则

①当f1（M-N）＞0时，由中值定理知，存在T11∈（0，M-N），使得f1（T11）=0，且AR1在区间［0，T11］单调递增，在区间［T11，M-N］单调递减。从而T*=T11。

②当f1（M-N）≤0时，此时在区间［0，M-N］上，f1（T）＜0，即AR1在区间［0，M-N］单调递增，从而T*=M-N。

（2）F1≥0，令。

①当T#1＜0时，f1（T）在区间［0，M-N］单调递减，从而f1（T）＜0，∀T∈［0，M-N］，即AR1在区间［0，M-N］单调递增，从而T*=M-N。

②当0≤T#1≤M-N时，f1（T）在区间［0，T#1］单调递增，在区间［T#1，M-N］单调递减。

（a）当f1（T#1）＞0且f1（M-N）≥0时，由中值定理知，存在T12∈（0，T#1），使得f1（T12）=0，且AR1在区间［0，T12］单调递增，在区间［T12，M-N］单调递减，从而T*=T12。

（b）当f1（T#1）＞0且f1（M-N）＜0时，由中值定理知，存在T13∈（0，T#1），使得f1（T13）=0；存在T14∈（T#1，M-N），使得f1（T14）=0，且AR1在区间［0，T13］单调递增，在区间［T13，T14］单调递减，在区间［T14，M-N］单调递增，从而T*=｛T*|T*∈｛T13，M-N｝，AR1（T*）=max｛AR1（T13），AR1（M-N）｝｝。

（c）当f1（T#1）≤0时，f1（T）≤0，∀T∈［0，M-N］，即AR1在区间［0，M-N］单调递增，从而T*=M-N。

③当T#1＞M-N时，f1（T）在区间［0，M-N］单调递增。

（a）当f1（M-N）＞0时，由中值定理知，存在T15∈（0，M-N），使得f1（T15）=0，且AR1在区间［0，T15］单调递增，在区间［T15，M-N］单调递减，从而T*=T15。

（b）当f1（M-N）≤0时，f1（T）≤0，∀T∈［0，M-N］，即AR1在区间［0，M-N］单调递增，从而T*=M-N。

证毕

引理2略

证明

①当f2（M-N）≥0时，显然，f2（T）≥f2（M-N）≥0，∀T∈［M-N，+∞），即AR2在区间［M-N，+∞）单调递减，从而T*=M-N。

②当f2（M-N）＜0且f2（T）|T→+∞＞0时，由中值定理知，存在T21∈［M-N，+∞），使得f2（T21）=0，且AR2在区间［M-N，T21］单调递增，在区间［T21，+∞）单调递减，从而T*=T21。

③当f2（M-N）＜0且f2（T）|T→+∞≤0时，显然，f2（T）＜0，∀T∈［M-N，+∞），即AR2在区间［M-N，+∞）单调递增，从而T*=+∞。

①当T#2≤M-N时，f2（T）在区间［M-N，+∞）单调递减。

（a）当f2（M-N）≥0且f2（T）|T→+∞≥0时，显然，f2（T）＞0，∀T∈［M-N，+∞），即AR2在区间［M-N，+∞）单调递减，从而T*=M-N。

（b）当f2（M-N）≥0且f2（T）|T→+∞＜0时，由中值定理知，存在T22∈［M-N，+∞），使得f2（T22）=0，且AR2在区间［M-N，T21］单调递减，在区间［T21，+∞）单调递增，从而

（c）当f2（M-N）＜0时，显然，f2（T）≤f2（M-N）≤0，∀T∈［M-N，+∞），即AR2在区间［M-N，+∞）单调递增，从而T*=+∞。

②当T#2≥M-N时，f2（T）在区间［M-N，T#2］单调递增，f2（T）在区间［T#2，+∞）单调递减。

（a）当f2（T#2）＞0，f2（M-N）≥0且f2（T）|T→+∞≥0时，显然，f2（T）＞0，∀T∈［M-N，+∞），即AR2在区间［M-N，+∞）单调递减，从而T*=M-N。

（b）当f2（T#2）＞0，f2（M-N）≥0且f2（T）|T→+∞＜0时，由中值定理知，存在T23∈［T#2，+∞），使得f2（T23）=0，且AR2在区间［M-N，T23］单调递减，在区间［T23，+∞）单调递增。从而

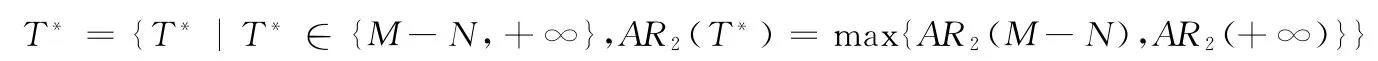
（c）当f2（T#2）＞0，f2（M-N）＜0且f2（T）|T→+∞≥0时，由中值定理知，存在T24∈（M-N，T#2），使得f2（T24）=0，且AR2在区间［M-N，T24］单调递增，在区间［T24，+∞）单调递减，从而T*=T24。

（d）当f2（T#2）＞0，f2（M-N）＜0且f2（T）|T→+∞＜0时，由中值定理知，存在T25∈（M-N，T#2），使得f2（T25）=0；存在T26∈（T#2，+∞），使得f2（T26）=0，且AR2在区间［M-N，T25］单调递增，在区间［T25，T26］单调递减，在区间［T26，+∞）单调递增，从而T*=｛T*|T*∈｛T25，+∞｝，AR2（T*）=max｛AR2（T25），AR2（+∞）｝｝。

（e）当f2（T#2）≤0时，显然，f2（T）≤0，∀T∈［M-N，+∞），即AR2在区间［M-N，+∞）单调递增。从而T*=+∞。

证毕

引理3略

证明

（1）当E2≤0时，显然，f3（T）单调递增，且f3（0）=-k＜0。

①当f3（T）|T→+∞＞0时，由中值定理知，存在T31∈（0，+∞），使得f3（T31）=0，且AR3在区间（0，T31］单调递增，在区间［T31，+∞）单调递减，从而易得T*=T31。

②当f3（T）|T→+∞≤0时，f3（T）≤0，∀T∈［0，+∞），即AR3在区间［0，+∞）单调递增，从而T*=+∞。

（2）当E2≥0时，令。

①当T#3≤0时，f3（T）在区间［0，+∞）单调递减，则f3（T）≤f3（0）＜0，∀T∈［0，+∞），即AR3在区间［0，+∞）单调递增，易得T*=+∞。

②当T#3＞0时，f3（T）在区间［0，T#3］单调递增，在区间［T#3，+∞）单调递减。

（a）当f3（T#3）＞0且f3（T）|T→+∞≥0时，由中值定理知，存在T32∈（0，T#3），使得f3（T32）=0，且AR3在区间［0，T32］单调递增，在区间［T32，+∞）单调递减，从而T*=T32。

（b）当f3（T#3）＞0且f3（T）|T→+∞＜0时，由中值定理知，存在T33∈（0，T#3），使得f3（T33）=0；存在T34∈（T#2，+∞），使得f3（T34）=0，且AR3在区间［0，T33］单调递增，在区间［T33，T34］单调递减，在区间［T34，+∞）单调递增，从而

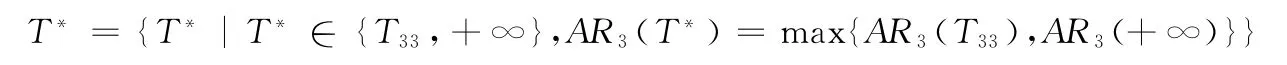
（c）当f3（T#3）≤0时，f3（T）≤f3（T#2）≤0，∀T∈［0，+∞），即AR3在区间［0，+∞）递增，易得T*=+∞。

证毕