基于Ramp-型需求及混合指数分布变质率的变质性物品库存系统的订货策略

赵连霞

（上海大学 管理学院，上海 200444）

在现代快速流转的库存管理中，对变质性物品（如水果、蔬菜、药品、化学品以及电子产品等）的库存控制问题越来越引起流通企业、经销商的重视。这是因为，如果忽略了物品的变质或损耗将影响库存成本，从而对企业的利润产生重要影响，所以对于有关运营系统的库存控制问题的研究就不可能忽略这些因素。从已有的文献来看，变质性物品的库存问题目前获得了广泛的研究。Whitin［1］最早对该问题进行了探讨，他主要考虑了时尚商品在规定存储期末的变质问题。Bakker等［2］对近年来变质性物品的库存模型的发展趋势作了完整的综述。

Mandal等［3］、Wu等［4］和Manna等［5］研究了一类需求率为Ramp-型的变质性物品的库存模型，此需求类型在新的消费品上市过程中最为常见，即需求率随新消费品上市时间推移而增至某一固定点时达到稳定。Deng等［6］将文献［3-4］中的研究条件扩展到库存系统的起始为缺货的情形。闵杰等［12］则通过考虑随时间变化的短缺量拖后率对库存订货策略的影响，建立了一类具有一般形式的短缺部分拖后的库存补充模型。李卫元等［13］研究了允许缺货情况下物品变质率服从威布尔分布的库存模型。刘斌等［14］研究了缺货损失高于补货成本易逝品的供应链契约。孙静春等［17］利用一类非线性成本库存模型，建立了一个生产者-订货商两级易逝品供应链运营模式，给出了供应链参与各方在无合作、合作及一体化3种模式下的易逝品生产订货模型。Cheng等［7-8］对具有类梯形需求模式的变质性物品库存问题进行了研究。更多的相关文献可参考文献［9-11，15-16，18］。

上述文献研究的库存模型中所考虑的需求率仅为线性或分段线性需求的情形。在实际的库存管理活动中，需求率并不都是线性的，而是在一定时期内可能是非线性增长的，在另一时期内则可能是市场需求饱和的稳定情况。同时，当库存成本和变质成本高于短缺成本时，库存短缺甚至是一种营销策略。在库存出现空缺期间，如果顾客愿意等待至下一次补货时取得商品，厂商仅承担缺货损失，不丧失销售机会；但有时部分顾客会转向购买其他商家的产品，原来的生产商则会遇到撤单现象，由此产生机会损失成本。因此，研究物品在现货销售和预销售条件下，允许短缺且部分拖后的库存控制有更加现实的意义。

本文研究了Ramp-型需求条件下具有混合指数分布率的变质性物品的库存模型。在假设需求率为分段函数形式下，分别就库存系统起始条件为备货销售和缺货预销售的情形建立了相应的库存模型，并且给出了模型的最优库存安排策略；同时，通过数值算例给出了该库存模型的最优安排策略的实现过程。

1 符号与假设

本文库存模型的建立用到以下记号：

D（t）—有限计划时期内的需求率，假设为Ramp-型，即

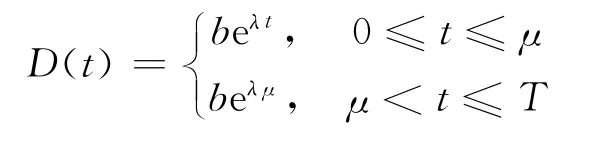
其中：μ为需求拐点；b为基本市场容量，为非负常数；λ∈（0，1）为常数。

I（t）— 时刻t的库存量，0≤t≤T

T— 固定的订货周期，t1为在订货周期内存货达到0的时刻，0＜t1＜T

物品开始变质的时间服从混合指数分布，物品的变质率

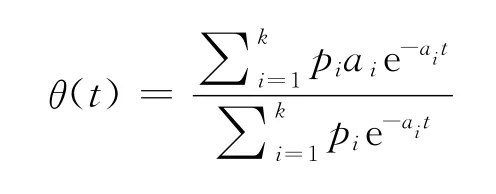
其中，

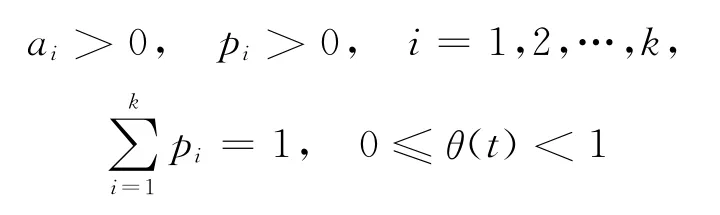
允许短缺但产生部分延后，延后率为e-δx，其中，x为顾客等待时间，δ为正常数

c1，c2，c3，c4—单位物品在单位时间内的库存费用、变质损失费用、缺货损失费用和撤单损失费用

S，Q—每个订货周期内最大库存量和订货量

Ci（t1），（i=1，3）—0≤t1≤μ单位时间平均费用

Ci（t1），（i=2，4）—μ≤t1≤T单位时间平均费用

2 现货销售条件下的系统库存模型及分析

根据符号及假设，可得本文所研究的库存系统：系统在t=0时刻进货，订购批量为Q，在［0，t1］时段库存量由于需求和物品本身的变质而下降，在t1时刻系统库存量减少到0。由于经销商订货需求的变化，在时段［t1，T］内发生缺货且缺货允许部分延后，故在［0，T］内的库存水平可用下述微分方程描述：

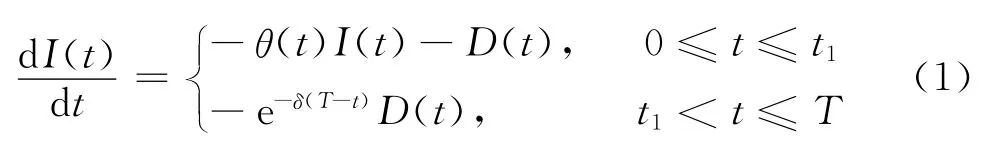
边界条件I（t1）=0。

由于物品需求满足Ramp-型，下面根据系统中库存量为0时刻所处阶段分为两种情形：

情形1当t1≤μ时，方程式（1）可表示为

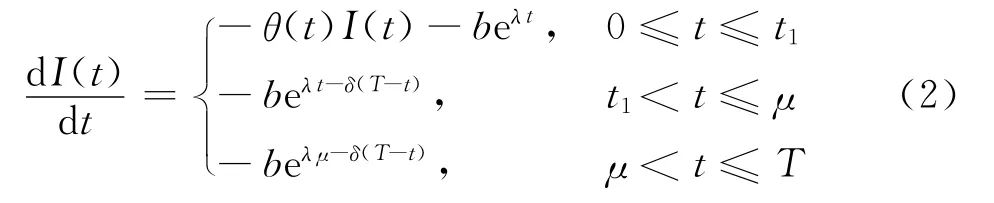
利用边界条件I（t1）=0，解上述方程组，可得

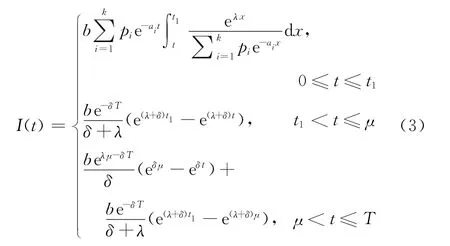
对于一个订货周期T，t=0时的库存水平

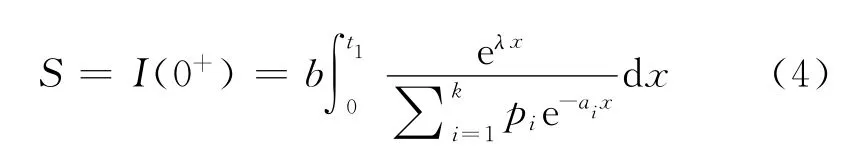
在时段［0，t1］内的变质损失量

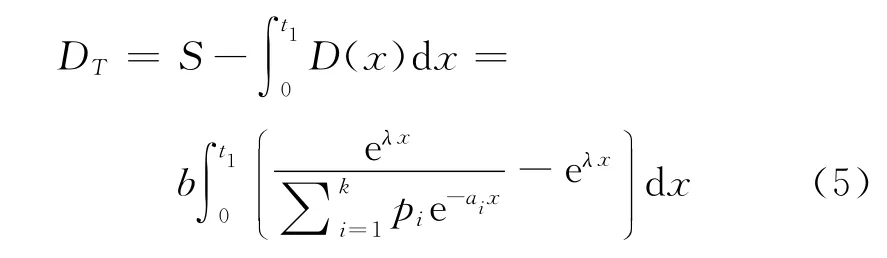
在时段［0，t1］内总的库存量

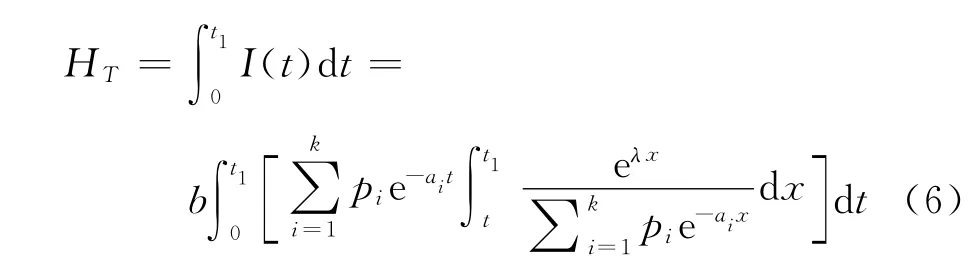
在时段［t1，T］内的缺货总量

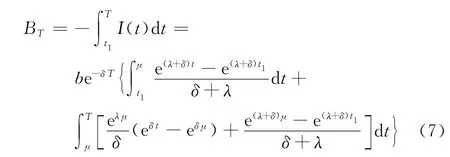
在时段［t1，T］内的失销总量

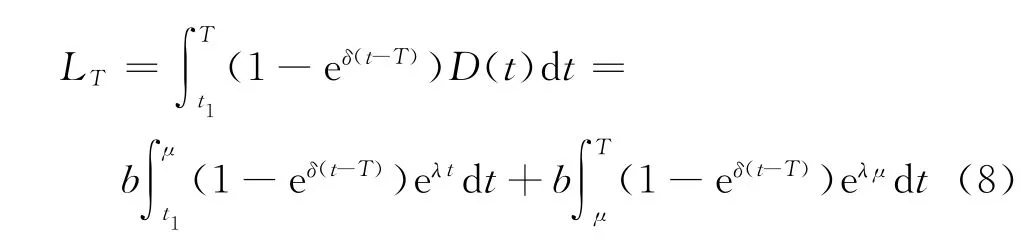
由式（5）～（8），即可得在条件t1≤μ≤T下，单位时间的平均费用为

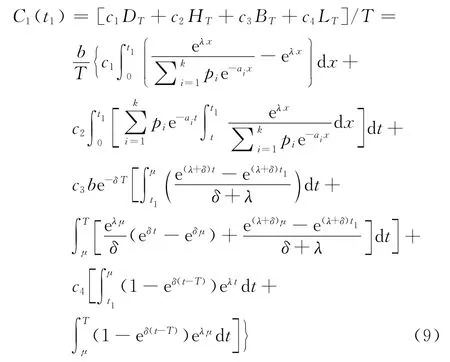
对C1（t1）分别求关于t1的导数，得

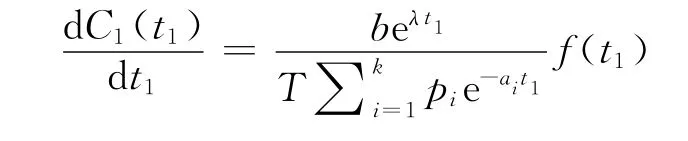
其中，

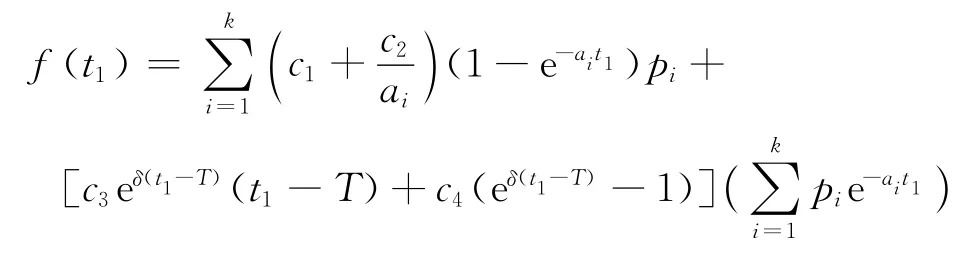
由

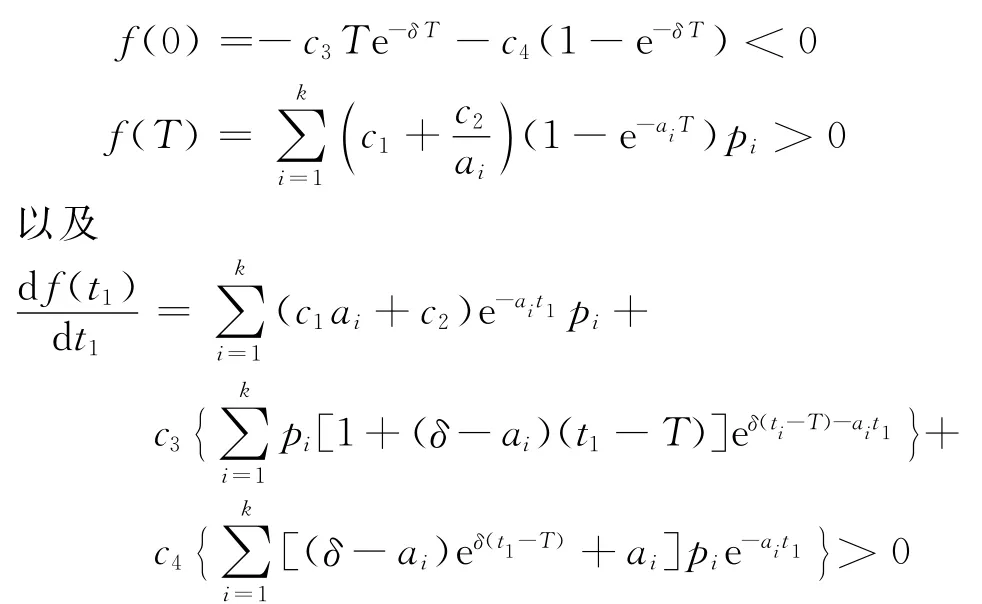
可得函数f（t1）存在唯一的零点，不妨设为，即为=0，又由于

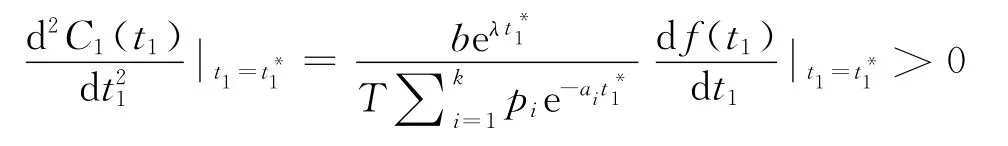
故可得：

引理1对于现货销售条件下的变质性物品库存系统，当0≤t1≤μ时，若f（μ）＞0，则平均费用C1（t1）在∈（0，μ）获得最小值；若f（μ）≤0，则平均费用C1（t1）在t1=μ获得最小值。

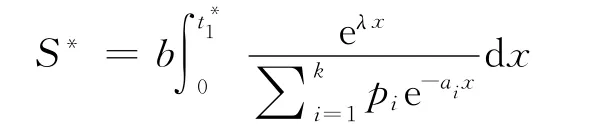
最佳订货量

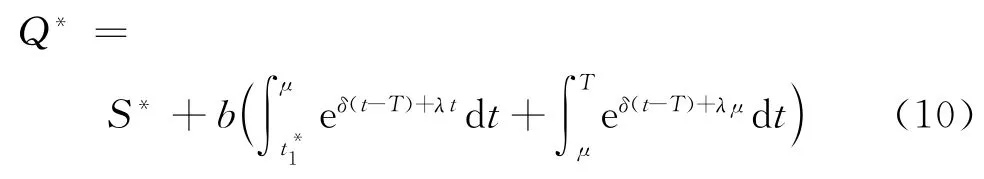
情形2当μ≤t1≤T时，方程式（1）为

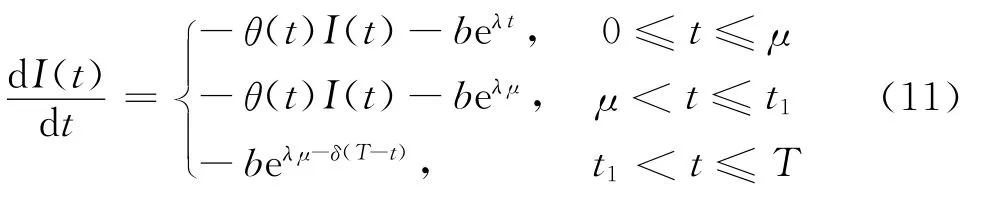
利用边界条件I（t1）=0，解得

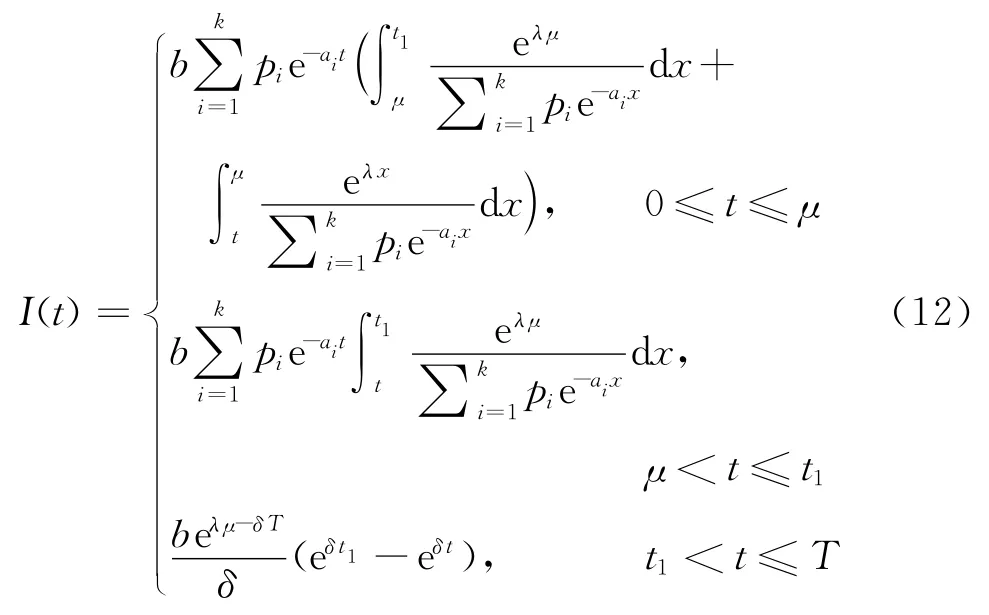
对于一个订货周期T，t=0时的库存水平

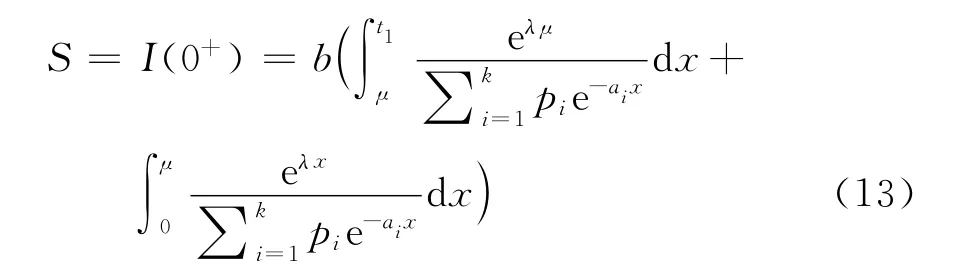
在时段［0，t1］内的变质损失

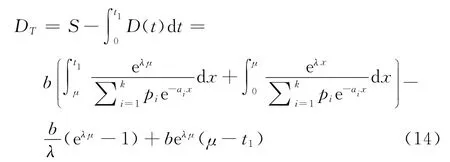
在时段［0，t1］内总的库存量

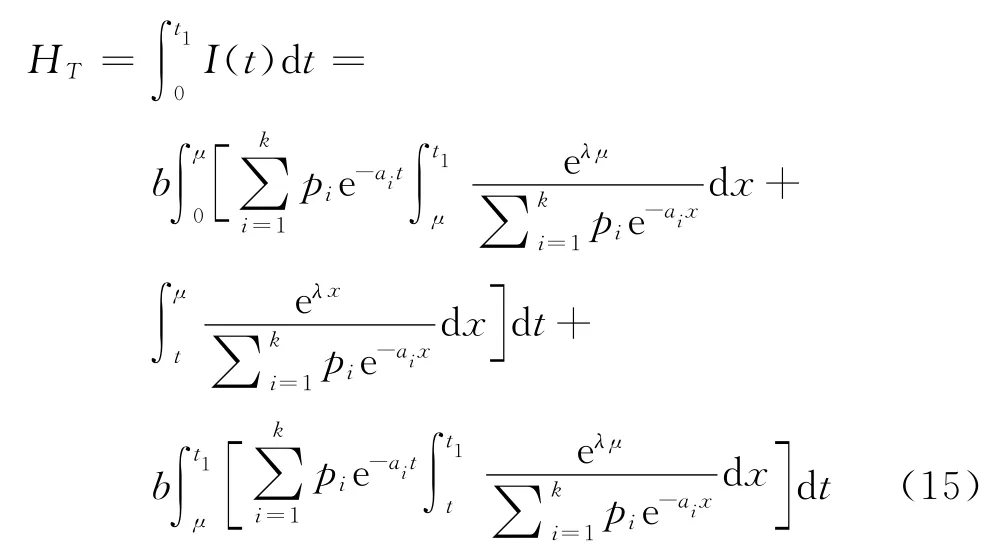
在时段［t1，T］内的缺货总量

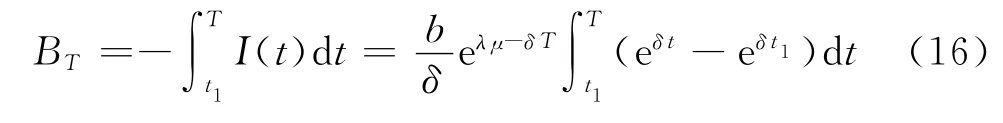
在时段［t1，T］内的失销总量

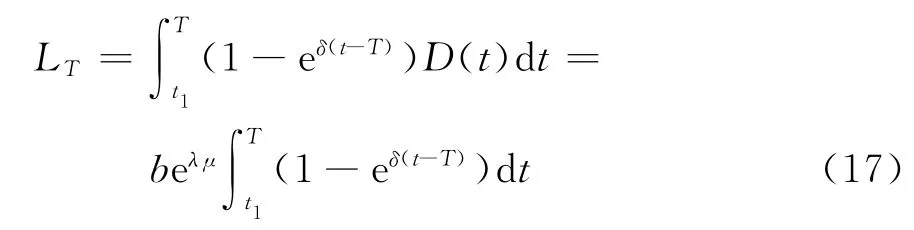
由式（14）～（17），可得在条件μ≤t1≤T下单位时间的平均费用为

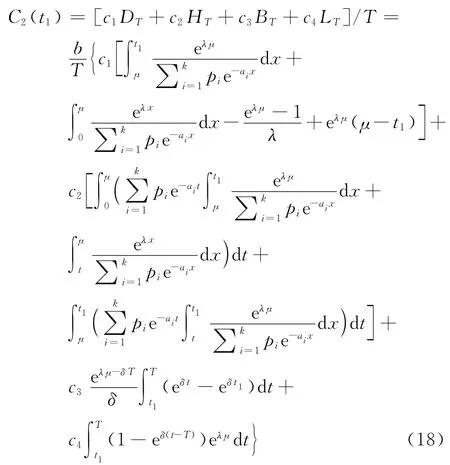
对C2（t1）求关于t2的导数，得

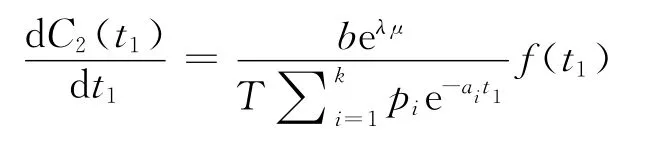
其中，

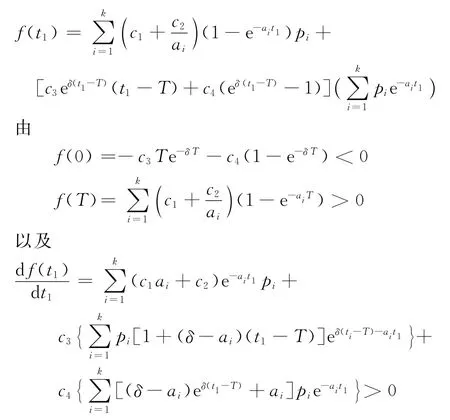
可得函数f（t1）存在唯一的零点，不妨设为，即为=0，又由于

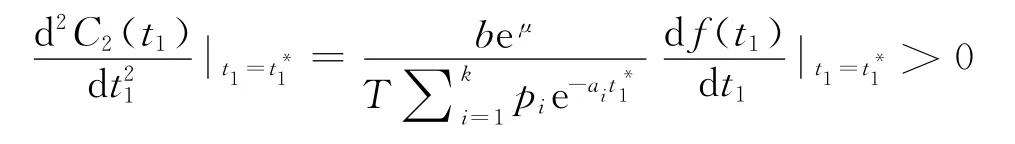
故可得：

引理2对于现货销售条件下的变质性物品库存系统，当μ≤t1≤T时，若f（μ）＜0，则平均费用C2（t1）在t1=∈（μ，T）获得最小值；若f（μ）≥0，则平均费用C2（t1）在t1=μ获得最小值。

因此，当μ≤≤T时，则最佳库存量

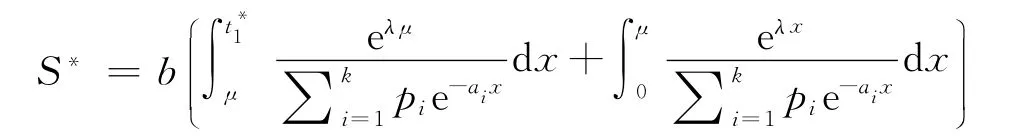
最佳订货量

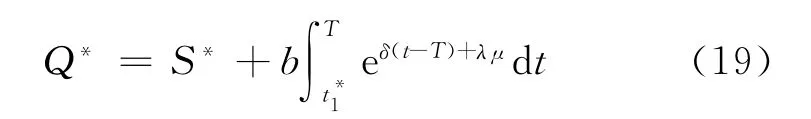
基于以上分析，可得［0，T］的现货销售条件下变质性物品库存系统的平均费用为

式中，C1（t1）和C2（t1）分别由式（9）、（18）确定。

综合以上分析，可得在现货销售条件下，允许短缺且部分延后的变质性库存系统的最优订货策略：

（1）输入参数c1、c2、c3、c4、ai、p i、b、λ、μ、T。

（2）求解方程f（t1）=0，不妨设所得解为，若∈（0，μ］，则最佳订货量和最小费用分别由式（10）、（9）确定；若∈（μ，T］，则最佳订货量和最小费用分别由式（19）、（18）确定。

3 预销售条件下的系统库存模型及分析

本节讨论系统起始为预销售情形。根据符号及假设，库存系统可描述为：库存系统在t=0 时刻没有库存，因而经销商不能及时给订单客户供货，直到上游制造企业在时刻t1给经销商补货同时补足客户订单且库存量达到最大S，订购批量为Q，在［t1，T］时段库存量由于进一步需求和库存变质而下降，故在［0，T］内的库存水平可用下述微分方程描述：

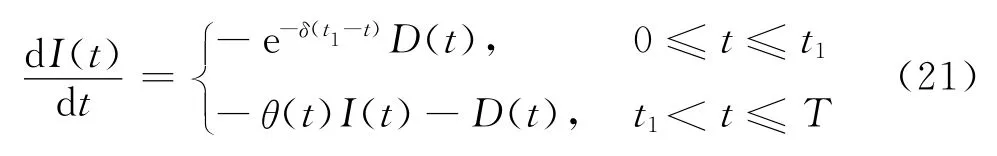
边界条件I（0）=I（T）=0。

由于物品需求为Ramp-型分段需求模式，下面根据系统中库存达到最大时刻所在阶段分为两种情况：

情形1当0≤t1≤μ时，方程式（21）为

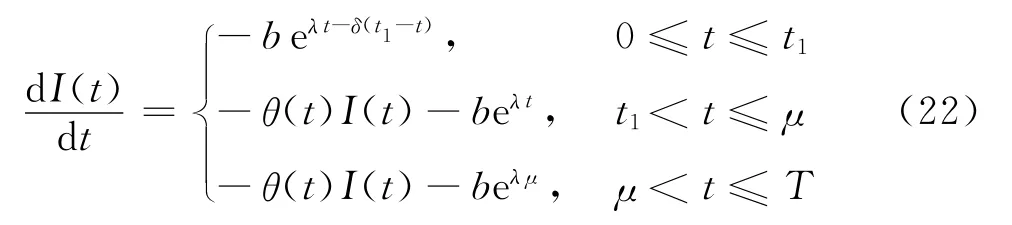
利用边界条件I（0）=I（T）=0，解上述方程组，可得

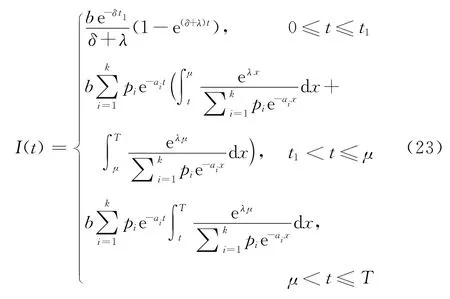
对于一个订货周期T，t=t1时的库存水平

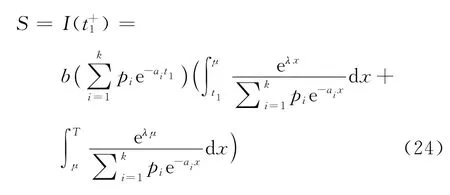
在时段［t1，T］内的变质损失

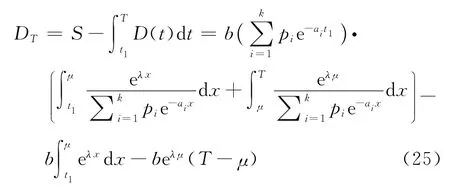
在时段［t1，T］内总的库存量

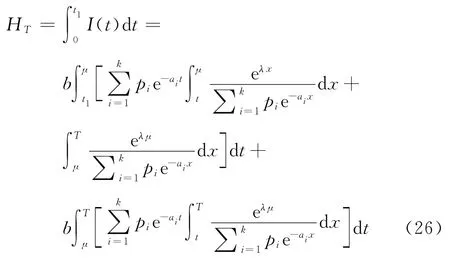
在时段［0，t1］内的短缺总量

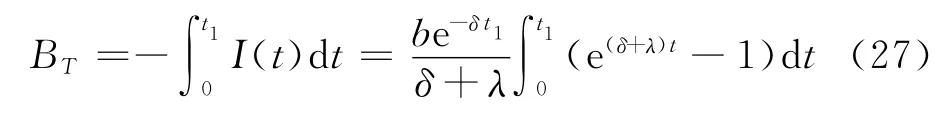
在时段［0，t1］内的撤单总量

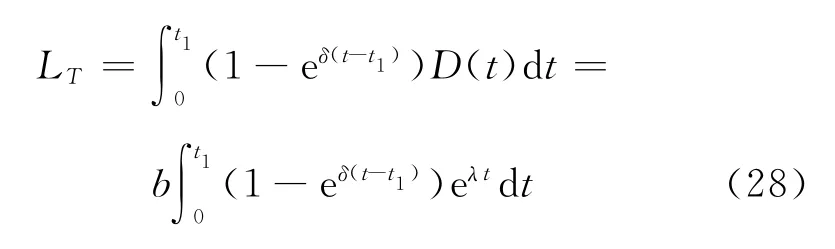
则在条件0 ≤t1≤μ下，单位时间的平均费用为

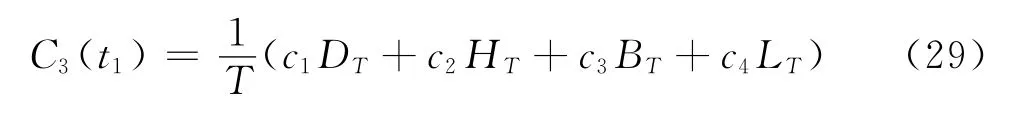
将式（25）～（28）代入式（29），并求关于t1的导数，可得

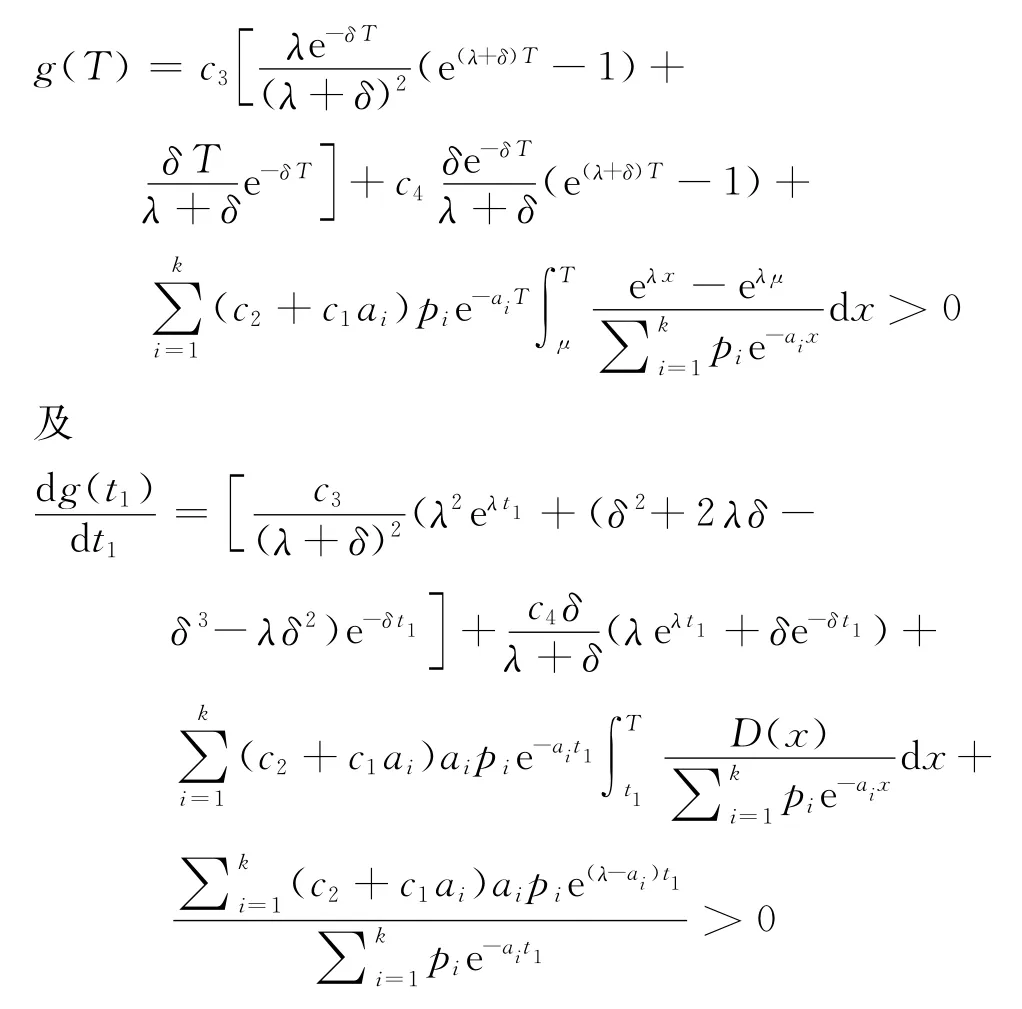
可得函数g（t1）存在唯一的零点，不妨设为，即为=0，因而有：

引理3对于预销售条件下的变质性物品库存系统，当0≤t1≤μ时，若g（μ）＞0，则C3（t1）在可获得最小值，其中=0；否则，C3（t1）在t1=μ获得最小值。

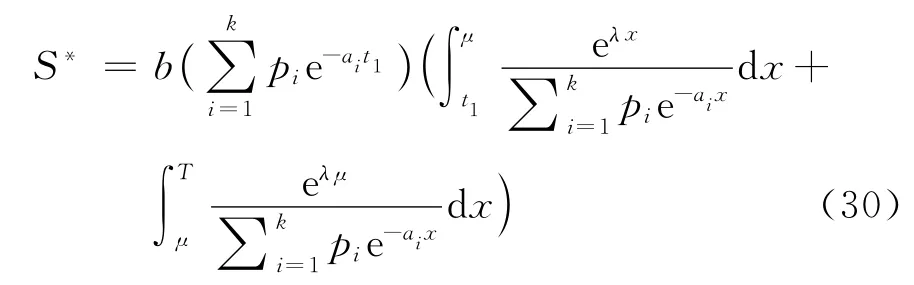
最佳订货量

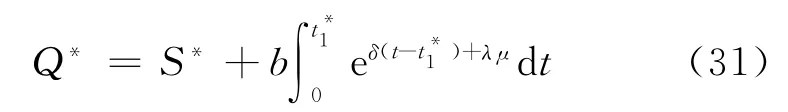
情形2当μ≤t1≤T时，方程式（21）为

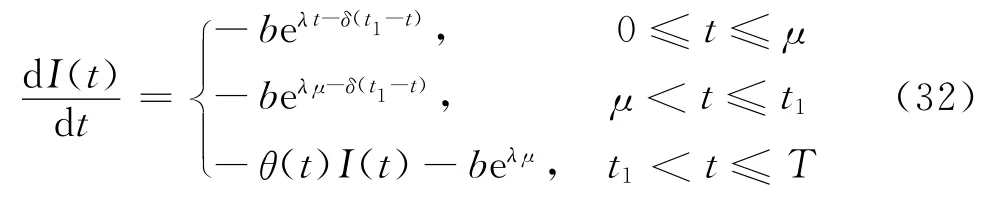
利用边界条件μ≤t1≤T，解上述方程组，可得

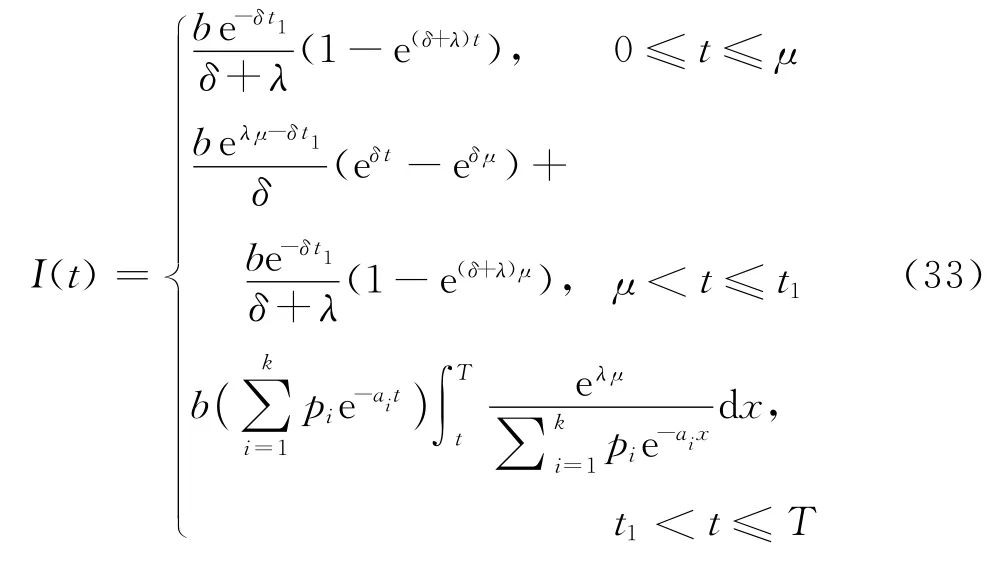
对于一个订货周期T，整个库存系统的库存水平

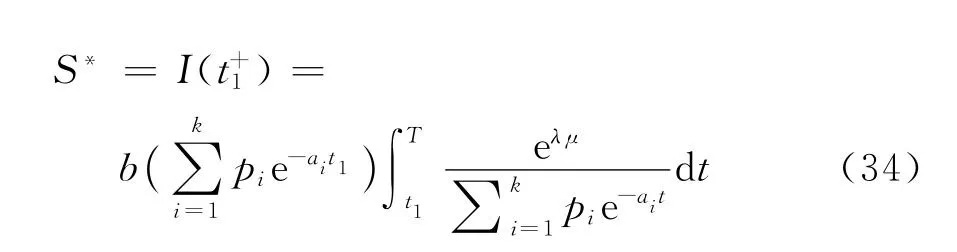
在时段［t1，T］内的变质损失

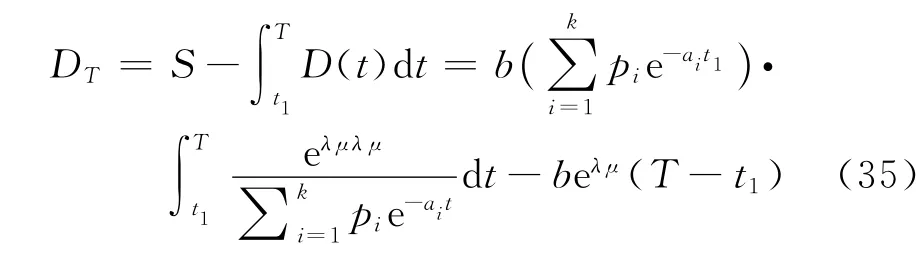
在时段［t1，T］内总的库存量

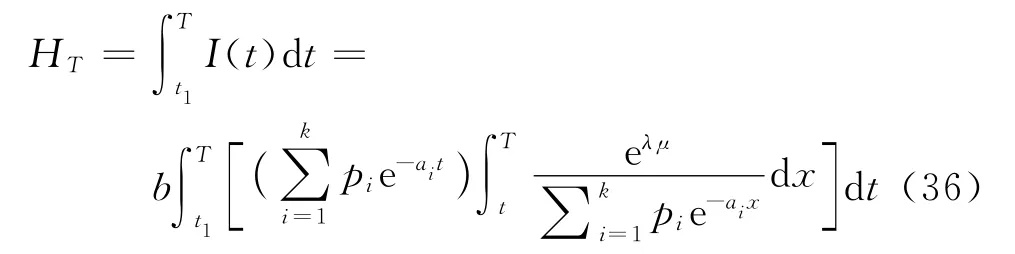
在时段［0，t1］内的缺货总量

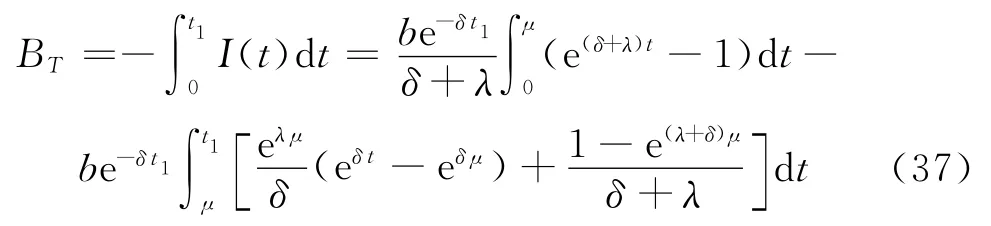
在时段［0，t1］内，由于缺货而造成的撤单总量

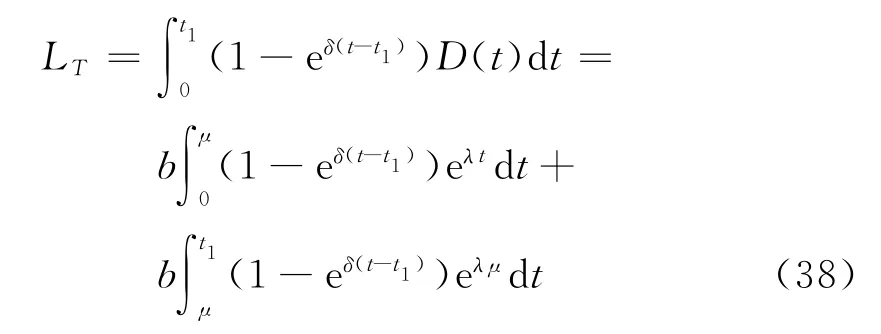
类似地，在条件μ≤t1≤T下，单位时间的平均费用为

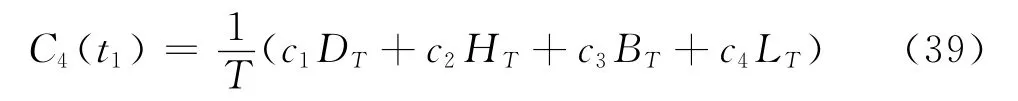
将式（35）～（38）代入式（39），并求关于t1的导数，即得

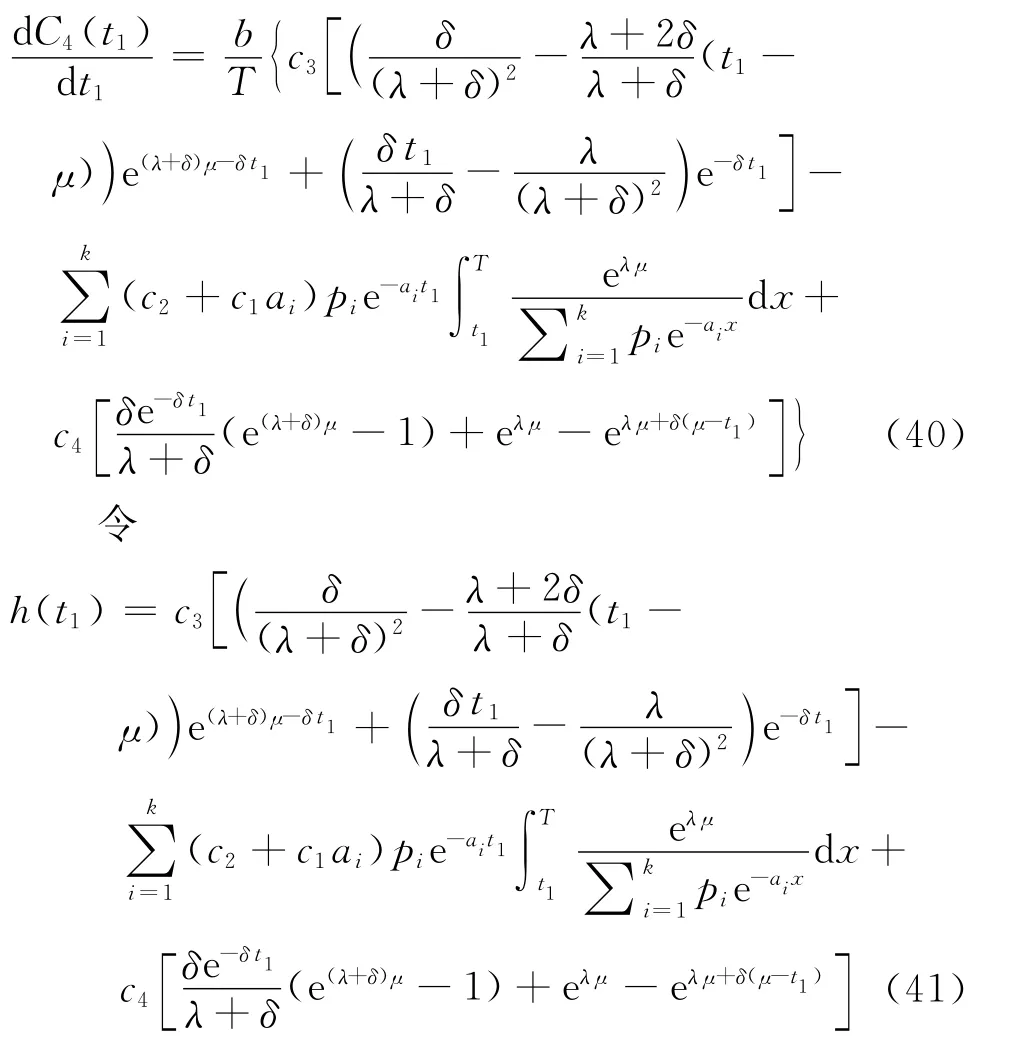
则有

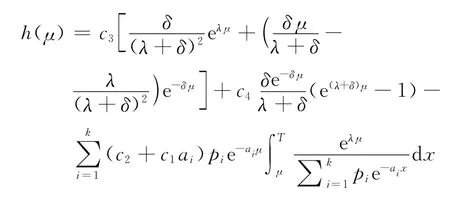
及

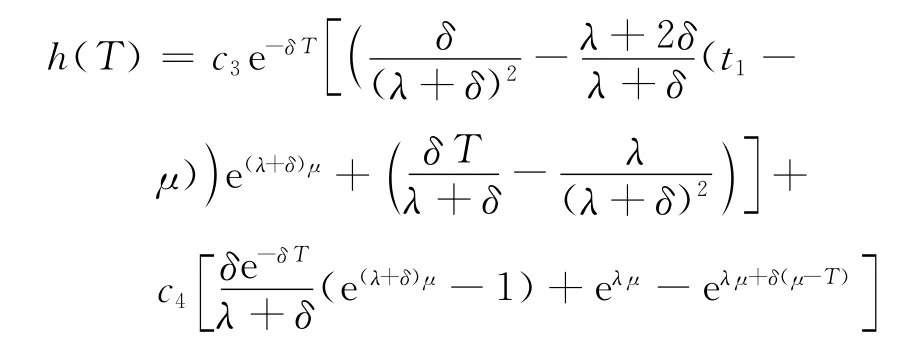
又由于

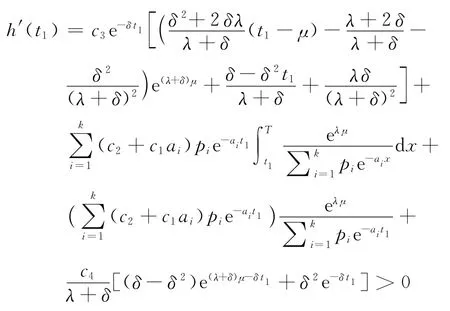
故h（t1）为一单调递增函数，因而可得：

引理4对于预销售条件下的变质性物品库存系统，当μ≤t1≤T时，若h（μ）h（T）＜0，则C4（t1）在t1=可获得最小值，其中=0；否则，C4（t1）在t1=μ获得最小值。

因此，当μ≤≤T时，则最佳库存量

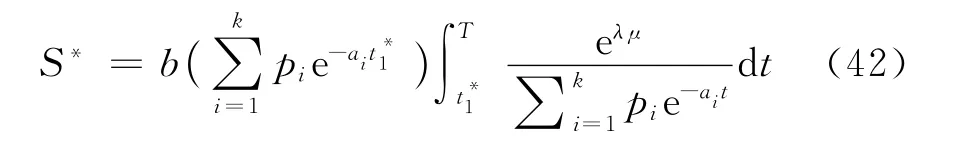
最佳订货量

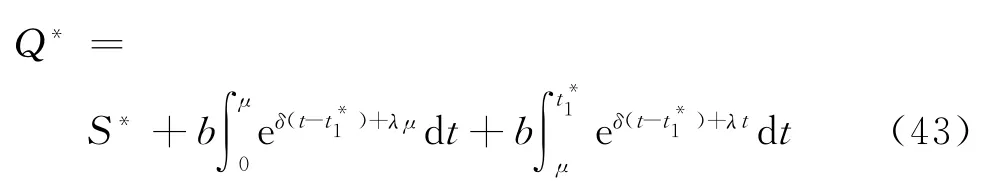
基于以上分析，可得［0，T］的预销售条件下，变质性物品库存系统的平均费用为

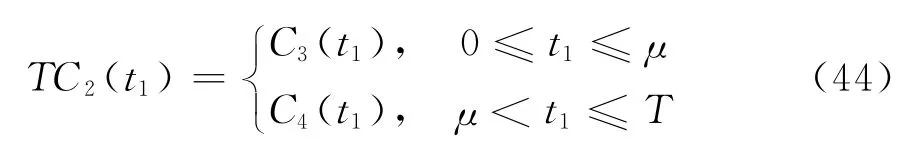
式中，C3（t1）和C4（t1）分别由式（29）和（39）确定。

综合以上分析，可得预销售条件下库存系统的最优策略算法：

（1）输入参数c1、c2、c3、c4、ai、p i、b、λ、μ、T。

（2）求解方程g（t1）=0，不妨设所得解为，若∈（0，μ］，则最佳订货量和最小费用分别由式（33）、（29）确定；否则=μ。

（3）求解方程h（t1）=0，不妨设所得解为，若∈（μ，T］，则最佳订货量和最小费用分别由（43）、（39）确定；否则，=μ。

4 数值实例及灵敏度分析

下面通过数值实例分析检验最优库存策略的实施过程。

例1假设某装配企业计划在一个周期内（T=12）制订某产品A 配件的订货计划。单位配件每天的库存保管费c1=5$，变质损失费用c2=10$，缺货损失费用c3=12$，撤单损失费用c4=4$，需求函数

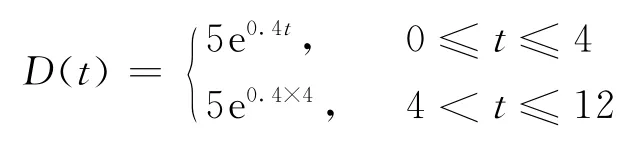
短缺延后率δ=0.2，变质率函数有关参数：

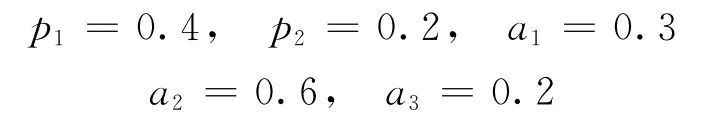
假设在现货库存系统体系下，利用Mathematica 9.0 软件计算可得：最佳缺货点=1.316，最佳订货量Q*=116.385，最小费用=278.394。

假设在预销售库存系统体系下，利用Mathematica 9.0 软件计算可得：最佳补货点=7.812，最佳订货量Q*=201.371，最小费用=571.836。

表1 参数λ对缺货点、最佳订货量和费用的影响（现货库存系统）

表2 参数μ 对缺货点、最佳订货量和费用的影响（现货库存系统）

表3 参数δ对缺货点、最佳订货量和费用的影响（现货库存系统）

表4 参数λ对订货点、最佳订货量和费用的影响（预销售库存系统）

表5 参数μ 对订货点、最佳订货量和费用的影响（预销售库存系统）

表6 参数δ对订货点、最佳订货量和费用的影响（预销售库存系统）

5 结语

本文研究了Ramp-型需求条件下变质性物品的库存系统最优策略模型。在假设需求率为有限容量的非线性函数形式下，分别就库存系统起始条件为现货销售和预销售情形下建立相应的库存优化模型，并且给出了模型的最优库存策略。同时，通过数值算例给出了该库存模型的最优库存策略的实现过程。结果表明，生产商提供现货销售或缺货销售情况下，库存系统的相关参数（如需求参数λ，需求拐点参数μ，缺货延迟参数δ）对经销商的订货策略产生重要影响：当需求参数较大时，订货量将会增加，由此产生的库存系统费用在现货销售情况下变化较为明显；当缺货延迟参数较大时，订货量明显减少，由此产生的库存系统费用在预销售情况下变化较为明显。因此对该类库存问题深入研究能为库存管理提供一些有益的启示。