基于相容性的区间直觉模糊信息的逆判问题

陈 岩，金 爽，杨依宁

（沈阳工业大学 理学院，沈阳 110870）

群组决策需要利用各专家给出的判断矩阵计算综合排序向量，若专家意见分歧较大时勉强进行集结，其结果往往难以具有说服力。如何衡量判断矩阵之间的差距，多大的差距可以容许，都可以用相容性予以表征。Saaty［1］针对群决策问题提出了相容性检验的概念，许多学者针对各类判断矩阵的相容性问题开展了大量的研究工作。对于确定性信息判断矩阵的相容性研究，学者们已经提出了较为成熟的相容性指标和相容性检验方法［1-2］。对于不确定性信息判断矩阵的相容性问题，徐泽水［3］针对区间模糊偏好信息判断矩阵给出其相容性定义及其性质。陈华友等［4］对不确定加性语言偏好信息判断矩阵的相容性及其在群组决策中的应用进行了研究。在此基础上，徐泽水［5］又针对基于直觉模糊偏好信息判断矩阵以及区间直觉模糊偏好信息判断矩阵的相容性进行研究，并给出了基于满意相容性调整其判断矩阵一致性的方法。Jiang等［6］对直觉乘性偏好信息的相容性问题进行了研究，并给出2个一致性调整的优化模型。

在众多的群决策问题中，如何有效解决专家之间意见的一致性与冲突性，将个人意见综合为可反映专家群体的一致性意见，以及从一致性的角度分析评判每个专家的判断水平（即逆判问题），是群决策研究的重要问题。刘万里［7］采用统计分析法，给出AHP 判断矩阵的逆判问题的方法。陈岩等［8］通过将互补判断矩阵和语言判断矩阵转化为互反判断矩阵，通过数理统计分析法解决群决策中互补判断矩阵的逆判问题；陈侠等［9］利用相对偏差给出了互补判断矩阵的评判方法；巩在武等［10］利用相关度给出了直觉模糊判断矩阵的逆判方法；夏梅梅等［11］在此基础上，通过相似度给出了区间直觉模糊判断矩阵的逆判方法。本文首先从区间直觉模糊数的相容性概念出发，根据其性质给出区间直觉模糊判断矩阵的一个相容性指标，以及衡量区间直觉模糊判断矩阵相容性的准则。然后对区间直觉模糊信息进行了一致性分析，进一步得出了基于相容性的区间直觉模糊判断矩阵的逆判方法。最后，通过算例验证了此方法的可行性和有效性。

1 基本概念和定义

定义1［14］设X是一个非空集合，

为直觉模糊集，其中，μA（x）、νA（x）分别为元素x属于集合X的隶属度和非隶属度，且满足条件

1-μA（x）-νA（x）为X中元素x属于X的犹豫度。

由于客观事物的复杂性和不确定性，μA（x）和νA（x）的值难以用精确的数值表示，而用区间数形式表示比较实际，故对直觉模糊集［12-13］进行了拓展，称

为区间直觉模糊集，其中，区间数μA（x）、νA（x）满足

根据文献14，区间直觉模糊集的基本组成部分是由元素x属于X的区间隶属度和区间非隶属度所组成的有序区间对（本文称为区间直觉模糊数）。为方便起见，将区间直觉模糊数的一般形式简记为（［a，b］，［c，d］），其中，

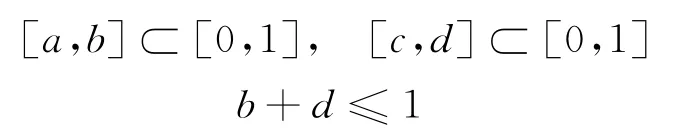
定义2［14］若m=（［al，au］，［bl，bu］），其中，

则称m为一个区间直觉模糊数。

定义3［14］若m=（［al，au］，［bl，bu］）为一个区间直觉模糊数，称mc=（［bl，bu］，［al，au］）为m的补数。且称区间直觉模糊数m与m c互补。

2 区间直觉模糊数的相容性

定义4设区间直觉模糊数

为m、n的相容度。

c（m，n）有下列性质：

（1）0≤c（m，n）≤1。

（2）自反性，即c（m，m）=0。

（3）对称性，即c（m，n）=c（n，m）。

证明

（1）因为

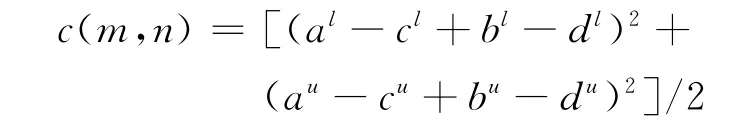
所以c（m，n）≥0，当al=1时，au=1，这时，bl=bu=0，即m=（［1，1］，［0，0］），要使c（m，n）取最大值，则n=（［0，0］，［0，0］），c（m，n）取最大值为1；同理，当

时，均使c（m，n）=1为最大值，即0≤c（m，n）≤1。

（2）、（3）易得，证明从略。

定理1对于区间直觉模糊数，具有互补一致性，即c（m，n）=c（mc，nc）。

证明根据定义3，有：

根据定义4，有：

设区间直觉模糊数m0=（［al，au］，［bl，bu］），简记 为m0=（a，b），其中，a=［al，au］，b=［bl，bu］。则a左移i个单位，b左移j个单位，得区间直觉模糊数

a右移i个单位，b右移j个单位，则得区间直觉模糊数

同理可得区间直觉模糊数

定理2对于区间直觉模糊数，具有平移一致性，即

证明根据定义4，有：

3 区间直觉模糊判断矩阵的相容性

定义5［15］设 判断矩阵A=［mij］n×n，其 中，mij=（μij，νij），i，j=1，2，…，n，为区间直觉模 糊数，满足条件：

则称A为区间直觉模糊判断矩阵。

定义6设A=［mij］n×n，B=［nij］n×n，为区间直觉模糊判断矩阵，其中：

为区间直觉模糊判断矩阵A、B的相容度，c（mij，nij）由定义4求得。

定义7设A=［mij］n×n，B=［nij］n×n，为区间直觉模糊判断矩阵，其中：

称A、B是完全相容的，若∀i，j∈N，均有mij=nij，即A=B。

由相容性性质（1）和定义6、7，易得如下定理：

定理3设A=［mij］n×n，B=［nij］n×n，为区间直觉模糊判断矩阵，则

（1）0 ≤C（A，B）≤n2，当A、B完全相容时，C（A，B）=0。

（2）自反性，即C（A，A）=0。

（3）对称性，即C（A，B）=C（B，A）。

证明从略。

定义8设A=［mij］n×n，B=［nij］n×n，为区间直觉模糊判断矩阵，其中：

指标

称为区间直觉模糊判断矩阵A、B的相容性指标。

由定理3可得，0≤SI（A，B）≤1，则A、B完全相容时，它们的相容性指标SI（A，B）=0。

定义9设A=［mij］n×n，B=［nij］n×n，为区间直觉模糊判断矩阵，若，则称A、B基本相容，其中为相容性指标的临界值。S.I.根据实际情况而定，一般取。

定义10设，k=1，2，…，m，均为区间直觉模糊判断矩阵，，ωi≥0，称为区间综合判断矩阵。

定理4由区间直觉模糊判断矩阵

集结的区间综合判断矩阵

也为区间直觉模糊判断矩阵。

证明对于区间直觉模糊判断矩阵

同理，易得

同理，易得：

定理5若，k=1，2，…，m，B=［nij］n×n，均为区间直觉模糊判断矩阵，如果SI（A（k），B）≤，则对于区间综合判断矩阵，k=1，2，…，m也有。

证明由SI（A（k），B），根据定义8，有

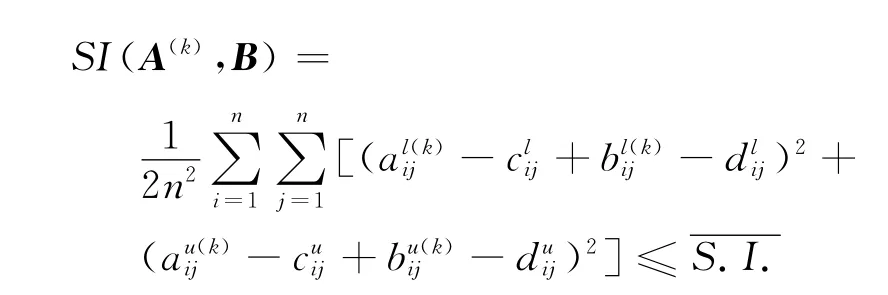
又因为

所以

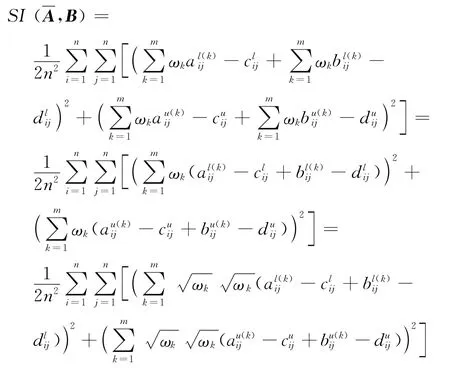
应用Cauchy-Schwarz不等式，上式可改写为

4 区间直觉模糊判断矩阵的一致性分析

定义11［16］设直觉模糊判断矩阵

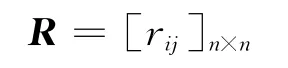
其中，rij=（μij，νij），若满足

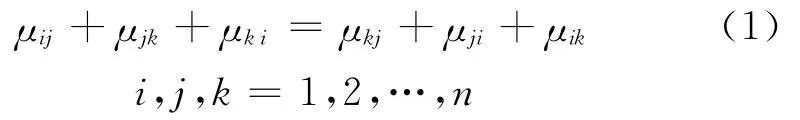
则称矩阵R为加性一致性直觉模糊判断矩阵。

由于μij=νji，νij=μji，故可得如下推论：

推论1设直觉模糊判断矩阵R=［rij］n×n，其中，rij=（μij，νij），若满足

则称矩阵R为加性一致性直觉模糊判断矩阵。

考虑直觉模糊判断矩阵加性一致性满足的条件和性质，现给出区间直觉模糊判断矩阵加性一致性的定义。

定义12设区间直觉模糊判断矩阵

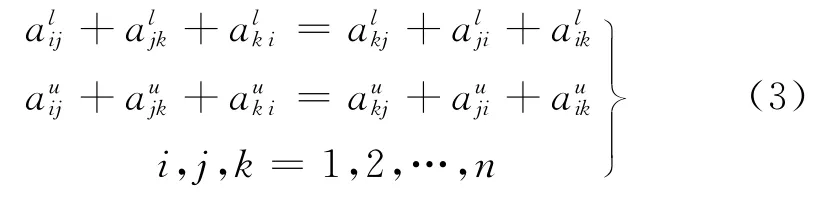
则称矩阵A为加性一致性区间直觉模糊判断矩阵。

由于

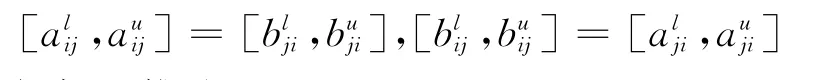
故可得如下推论：

推论2设区间直觉模糊判断矩阵

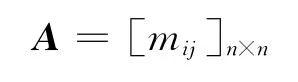
则称矩阵A为加性一致性区间直觉模糊判断矩阵。

定理6令s（ml）=al-bl，s（mu）=au-bu，如果

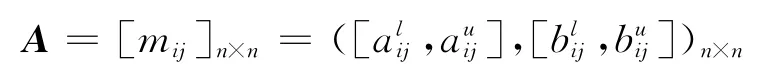
为加性一致性区间直觉模糊判断矩阵，当且仅当

时成立。

证明必要性。由

为一致性区间直觉模糊判断矩阵，根据式（3），得：

因为

则上式可改写为：

且s（ml）=al-bl，s（mu）=au-bu，则：

上面的证明逆推即为充分性，证明从略。

5 基于相容性的逆判方法

根据前面的讨论，可以获得一组加性一致性区间直觉模糊判断矩阵

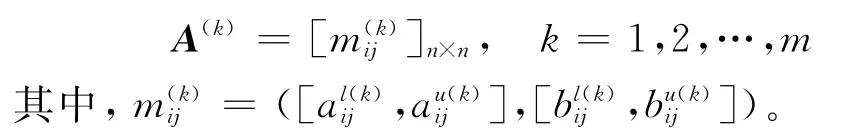
根据定理4和定义12，易得如下定理：

定理7由加性一致性区间直觉模糊判断矩阵，k=1，2，…，m，集结的区间综合判断矩阵

也为加性一致性区间直觉模糊判断矩阵。

证明从略。

根据相容度的性质，将相容性指标作为专家评判的标准，SI（A（k））表示专家所做出决策与集体决策的贴近程度，相容性指标越小，则专家决策越接近集体决策，专家评判的水平越高。

根据前面的讨论，基于相容性的区间直觉模糊判断矩阵逆判方法的过程如下：

（1）对于一个群决策问题，决策者ek（k=1，2，…，m）对所有方案集进行比较，并构造区间直觉模糊判断矩阵，满足

（2）将所有区间直觉模糊判断矩阵R（k）=，k=1，2，…，m转化为加性一致性区间直接模糊判断矩阵。

（4）计算每一个区间直觉模糊判断矩阵R（k）和加性一致性区间综合判断矩阵的相容性指标。

6 算例分析

例 5个决策者ek（k=1，2，3，4，5）分别对5个方案x i（i=1，2，3，4，5）进行评估，且决策者的权重向量，得到5个区间直觉模糊判断矩阵R（k）（k=1，2，3，4，5）：

应用基于区间直觉模糊判断矩阵逆判方法的步骤，可得：

（1）已获得区间直觉模糊判断矩阵R（1）、R（2）、R（3）、R（4）、R（5）。

（2）将所有区间直觉模糊判断矩阵

转化为加性一致性区间直接模糊判断矩阵

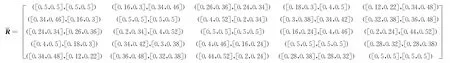
（4）计算每一个区间直觉模糊判断矩阵R（k）（k=1，2，3，4，5）和加性一致性区间综合判断矩阵的相容性指标（k=1，2，3，4，5），得：

（5）根据相容性指标的大小对专家进行排序。

因此，专家评判水平为e5≻e3≻e2≻e1≻e4。

7 结语

本文通过研究区间直觉模糊数的相容度性质，提出了区间直觉模糊判断矩阵相容度及相容性指标的定义，进一步分析了区间直觉模糊判断矩阵的加性一致性；通过专家给出的信息偏好，给出了基于相容性指标区间直觉模糊信息的逆判方法。有关区间直觉模糊信息的乘性一致性充分必要条件以及应用相容性进行一致性的调整方法可能是未来研究工作的方向。