聚焦高中数学解题中化归转化思想的应用

◇ 山东 李秀振

聚焦高中数学解题中化归转化思想的应用

◇ 山东 李秀振

高中数学学习的过程一般是按照“概念和定理的理解记忆—知识点的应用训练”这一顺序.后者实际上就是化归思想的应用的过程.因此在学习中应加强常规化归思想方法的积累、应用,进而提高解题效率.

1 生与熟的转化

数学能够借助题型变化来对学生知识掌握程度加以深度考查,针对我们不熟悉的题型,学生应具备“化归转化”思想,构建辅助元素,建立问题和条件间的联系.

例1 在平面直角坐标系xOy中,设定点A(a, a),P是函数(x＞0)图象上一动点,若点P、A之间的最短距离为则满足条件的实数a的所有值为________.

若a≤2,则当t＝2时,PA2取得最小值.从而有(2－a)2＋a2－2＝8,解得a＝－1,a＝3(舍去);

若a＞2,则当t＝a时,PA2取得最小值.从而有a2－2＝8,解得或(舍去).故满足条件的实数a的所有值为

2 繁与简的转化

某些题目本身难度不大,但其题干叙述较为模糊,学生分不清已知条件之间的关系.针对这一情况,就可借助转化与化归思想实现化繁为简的目的.

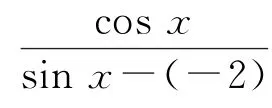
初看此题不知如何下手,但若具备“数形结合”思想的话,可将其变形为的形式,从而联想到令y＝便可将解题内容定位为点(－2,0)、(sinx,cosx)连线斜率的最大、最小值问题.

3 正与反的转化

逆向思维是一种重要的发散性思维,尤其是在正面解题运算量大且复杂的情况下可采用反面求解.

例3 2b2－2b＋c＝0,2a2－2a＋c＝0,a－b＝c,求c值.

本题学生很容易想到配方消元,但由于其所含未知元素太多,运算复杂,故应引导学生借助“逆向思维”的办法.

a和b相当于一元二次方程2x2－2x＋c＝0的解,再利用根与系数的关系得ab＝－c/2,a＋b＝1,结合a－b＝c便可获得答案.

又如计算3－32－33－34－35－36－37－38－39＋310,应第一时间确定逆向思维分析思想,利用从右到左的“3n－3n－1＝3n－1”关系来计算.

4 数与形的转化

例4 已知x、y、z都是正实数,求证

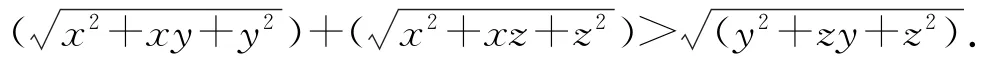
从已知条件所给形式看与“三角形两边之和大于第三边”这一定定理颇有相似之处,而开方式又能和余弦定理相类比,故而如此构建三角形便可解答此题.

5 特殊与一般的转化

例5 函数y＝f(x)的定义域为(0,＋∞),且对定义域内的任意x、y都有f(x·y)＝f(x)＋f(y),且f(2)＝1,则的值为( ).

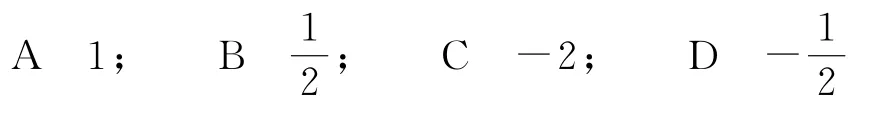
由已知条件“对于定义域内的任意x、y都有f(x·y)＝f(x)＋f(y)”联想特殊的对数函数具有此性质,故可令f(x)＝logax.

又因为f(2)＝1,即loga2＝1,所以a＝2,所以

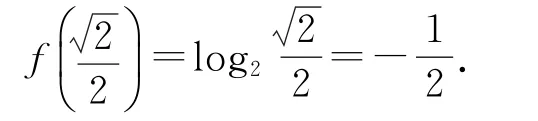
综上所述,教师于平日教学活动中,应有意识地对学生的化归转化思想加以引导和培养,从而有效促进解题效率的提升.

山东省邹平县魏桥中学)