曲线有共交点情境中定点问题的探究

◇ 江苏 顾天荣

曲线有共交点情境中定点问题的探究

◇ 江苏 顾天荣

在圆锥曲线问题中常常设置这样一类问题情境:直线与一种曲线有2个交点,而这2个交点恰恰又在另一个动曲线的轨迹上,问这个动曲线是否过定点.对于这类问题如何处理、有何策略,值得深思和探索.

1 兴趣引起:一道质量检测引发的思考

一次质量检测过程中笔者发现在一种曲线共交点问题情境下定点问题解决的过程比较烦琐,于是激发了笔者对这类问题求解规律的寻找.

例1 椭圆O的中心在原点,长轴在x轴,右顶点A(2,0)到右焦点的距离与它到左准线的距离之比为不过点A的动直线交椭圆O于P、Q2点.

(1)求椭圆的标准方程;

(2)证明P、Q2点的横坐标的平方和为定值;

(3)过点A、P、Q的动圆C,已知动圆过A、B2定点,求点B坐标.

(1)椭圆方程为x2＋4y2＝4.

(2)略.

(3)解题关键在于能够写出动圆C的方程,在圆心和半径不明确或不易用参数表示时,常会选择圆的一般方程,因此可设动圆C的方程为x2＋y2＋Dx＋Ey＋F＝0,如何求解D、E、F是本题的难点.经过分析其实不难发现这个问题的突破口:椭圆和动圆C同时过P、Q2点,而P、Q在直线上,联想到直线与曲线交点问题的求法(将直线与二次曲线联立方程组,化为一元二次方程求解),因此,把椭圆和直线联立、把动圆和直线联立化简后的一元二次方程对应系数成比例.

将椭圆与直线联立得x2＋2mx＋2m2－2＝0.

将圆与直线联立得

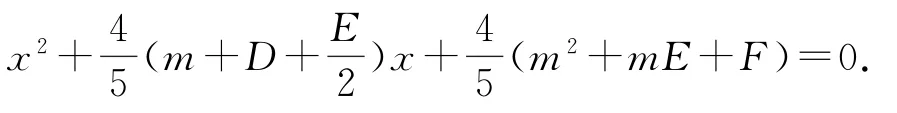
上述2方程同解,对应系数成比例,即

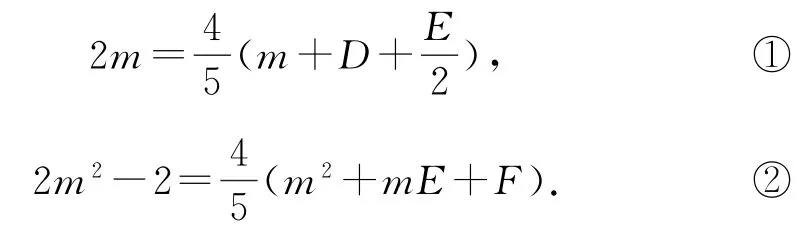
由式①得E＝3m－2D,又点A在圆上,所以F＝－2D－4,将此2式代入式②可得

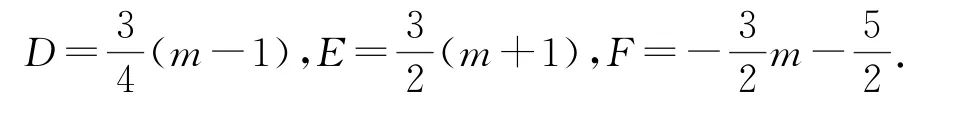
2 追根溯源:寻找这类问题高考的原型

透过上述问题不难发现笔者选择的方法关键在于利用了2曲线与同一条直线的共交点,从而将交点转化为直线与曲线联立方程组同解的问题.笔者认为这才是出题者的本来意图.智慧是一代代传承的,于是笔者试图从模拟考卷和历年的高考真题中搜寻这种问题的高考原型.笔者在2008年的江苏高考卷中到了这样一道真题:其参考答案的解决思路即为2曲线与同一直线共交点时,直线与曲线联立所得的2个方程组同解,则所得一元二次方程的对应系数成比例.

例2 在平面直角坐标系xOy中,设二次函数f(x)＝x2＋2x＋b(x∈R)的图象与2个坐标轴有3个交点,经过这3个交点的圆记为C.

(1)求实数b的取值范围;

(2)求圆C的方程;

(3)圆C是否经过定点,请证明你的结论.

3 反思升华:剖析简化计算的关键玄机

回顾这2道问题,其基本思路与定点问题解决的策略是相同的,即通过对动曲线方程特征的分析来确定定点.与以往最大的不同在于确定动曲线方程的方式,这恰恰是这类问题处理的最大特色和计算简化的关键玄机.例2在确定动圆方程中D、E、F时,可将二次函数与坐标轴交点坐标以b来表示,再以点在圆上为桥梁建立3个方程组,求解D、E、F.当我们实际操作后发现,无论是计算层面还是思维层面都显得无比复杂.首先,在计算层面,姑且不论三元方程组解题的计算量,就是带参数的一元二次方程求解,也是相当复杂,更不用说求解圆的方程;其次,在思维层面上,寻找3个等量关系来建立方程组,并不是每次均可用点在曲线上来处理,比如例1就需要3种不同的关系:点在圆上、圆心在PQ垂直平分线上、根与系数的关系,这样的思维量对于处在考场中的学生而言实在太大.反观利用曲线共交点—方程同解—对应系数成比例,我们处理的思维运算只有一个,即方程同解、对应系数成比例.若把前一种称为复合思维,而这种方式仅仅是一种单向思维,思维运算的程度被大大简化.

江苏省兴化市文正实验学校)