拉弯矫直延伸率的计算及试验分析
2016-08-16戚向东连家创董志奎
戚向东 连家创 董志奎
1.燕山大学国家冷轧板带装备及工艺工程技术研究中心,秦皇岛,0660042.燕山大学,秦皇岛,066004
拉弯矫直延伸率的计算及试验分析
戚向东1,2连家创1,2董志奎2
1.燕山大学国家冷轧板带装备及工艺工程技术研究中心,秦皇岛,0660042.燕山大学,秦皇岛,066004
针对目前拉弯矫直过程缺少完整的数学求解模型的问题,根据矫直带材在拉弯过程中,中性层偏移量及延伸率的计算模型,给出了拉弯矫直张力、矫直力和延伸率的计算方法。通过计算与工业试验,分析了拉弯矫直机矫直规程对残余延伸率的影响,并验证了计算模型的精确性。
拉弯矫直;张力;延伸率;计算模型;工业试验
0 引言
拉伸和弯曲联合作用的辊式拉弯矫直方法是比单纯拉伸或单纯弯曲更有效的矫直方法[1-2]。对钢带而言,延伸率一般为2%已经足够,而铝带的延伸率应取3%,最大不超过5%[3]。目前,拉弯矫直相关的研究大都以张力为已知量进行分析,而拉弯矫直过程中,张力、弯曲曲率、延伸率三者相互作用,互为影响[4-5]。拉弯矫直规程通过拉弯矫直机出口处带材的总延伸率和各弯曲辊的压下量进行设定,实际矫直过程中的入口张力、出口张力及各矫直段张力是跟随延伸率设定值及弯曲辊的压下量而定的,是未知量。在拉弯矫直的过程中,带材延伸率是一项重要的控制目标,它影响着带材的机械性能。因此,确定张力、弯曲曲率、延伸率三者之间的相互关系,建立完整的拉弯矫直计算理论是计算延伸率及指导拉弯矫直规程设定的基础。
1 拉伸弯曲中性层偏移距及弯曲力矩的计算
拉弯矫直过程中,张力不仅降低了带材的塑性弯曲力矩和弹复曲率,而且使中性层相对平分层(中心线)移动了一定距离,从而使带材产生一定的延伸率。
如图1所示,压缩区产生塑性变形时,由于张力σp的作用,中性层相对平分层(中心线)移动了距离a。距离a可以根据水平方向力的平衡条件确定:
[(h/2+a-z0)(σs+σH)-
(h/2-a-z0)(σs+σL)]=2hσp
(1)
(2)
(3)
式中,σs为材料屈服强度,MPa;σp为带材所受张应力,MPa;h为带材厚度,mm;b为带材宽度,mm;z0为开始产生塑性变形的金属层距中性层的距离,mm;σH为拉伸层表面应力,MPa;σL为压缩层表面应力,MPa;η为强化系数,即强化模数E1与弹性模数E的比值,η= E1/E。

图1 压缩区产生塑性变形时应力沿高度的分布
将式(2)、式(3)代入式(1),令ξ=σp/σs,整理得
(4)
(5)
2 拉弯过程延伸率的计算
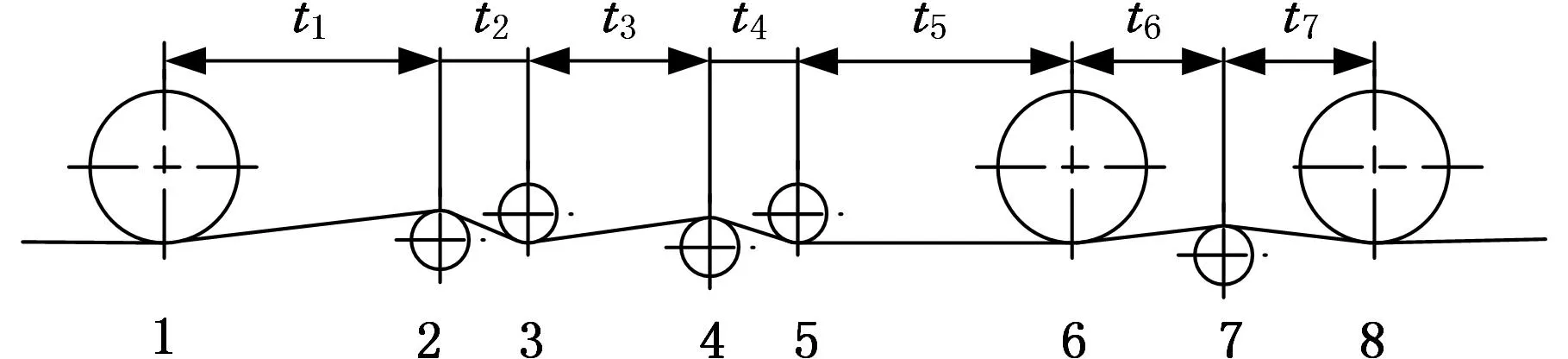
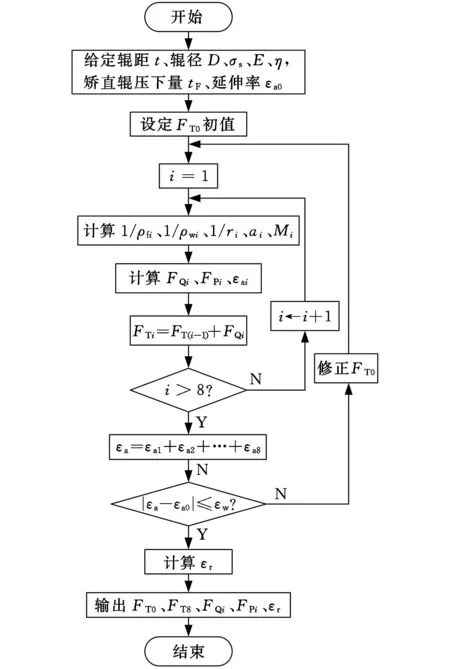
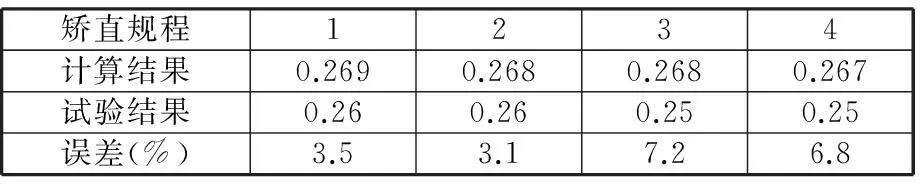
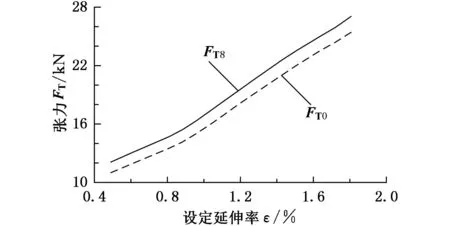
拉弯过程中,张力使中性层相对平分层(中心线)移动了距离a,从而使平分层产生了拉伸变形。如图2所示,z0≥a时,平分层只产生弹性变形,不产生塑性变形;z0 (a)z0≥a (b)z0 带材压缩区发生塑性变形时,根据平面变形假设(图2),平分层变形量为 εa=εsa/z0 (6) 式中,εs为开始产生塑性变形金属层的变形量,εs=σs/E。 εa是加载时的变形量,应减去卸载时弹性恢复的变形量εe才是残余变形量εr,即 εr=εa-εe (7) 考虑材料强化时,平分层弹性恢复变形量为 εe=(σs+Δσ)/E (8) (9) 把式(9)代入式(8)并整理可得 (10) 把式(6)、式(10)代入式(7),可得带材平分层(中心线)的残余变形量 (11) 如果有多次符合延伸条件的拉弯过程,则总延伸率等于各次拉弯过程的总和,即 (12) 图3是一种常用的拉弯矫直机辊系(由2组弯曲辊组和1组矫平辊组组成)布置示意图,拉弯矫直机通过前后S辊提供张力,并通过安装在其上的编码器测定延伸率,保证延伸率设定值;2号和4号矫直辊及7号矫平辊通过压上装置给定插入量;1号、6号和8号辊为压辊。 图3 拉弯矫直机辊系布置图 图4是矫直带材受力示意图,各辊出口处水平张力可根据水平力平衡条件得 (13) 式中,FT0为带材后张力,N;FQj为j号辊对带材的水平作用力,N。 图4 矫直带材受力示意图 根据文献[1]可得水平力 (14)其中,FPi为垂直力,N;f为矫直辊的滚动摩擦力臂,mm;ρ为矫直辊轴承摩擦圆半径,mm;R为矫直辊半径,mm;M为弯曲塑性力矩,计算公式参见文献[1],N·mm;1/r为残余曲率,1/mm;ky为恢复系数,数值在0~1之间,ky=0说明弹性功完全恢复,ky=1说明弹性功全部不能恢复;1/ρf为弯曲曲率,计算公式参见文献[5],1/mm。 如式(14)所示,如果要求解水平力FQi,首先要计算垂直力FPi。对1~5号辊各个辊处的轧件用截面法截开单独分析,可分别写出平衡方程。 第2辊的平衡方程为 FP1t1-(FT0+FQ1)tF2=M2式中,t1为辊间水平中心距,m;tF2为第2矫直辊压下量,m。 从而可求得 FP1=[M2+(FT0+FQ1)tF2]/t1 (15) 第3辊的平衡方程为 FP1(t1+t2)-FP2t2+FQ2tF3=-M3 从而可求得 FP2=[M3+FP1(t1+t2)+FQ2tF3]/t2 (16) 同理,可求得FP3、FP4: FP3=[M4-FP1(t1+t2+t3)+FP2(t2+t3)+ (FT0+FQ1+FQ3)tF4]/t3 (17) FP4=[M5+FP1(t1+t2+t3+t4)-FP2(t2+t3+t4)+ FP3(t3+t4)+(FQ2+FQ4)tF5]/t4 (18) 需要在5号辊处带材出口端对4号辊列出关于FP5的平衡方程: FP5t4-(FT0+FQ1+FQ2+FQ3+FQ4)tF4=M4 从而可求得 FP5=[M4+(FT0+FQ1+FQ2+FQ3+FQ4)tF4]/t4 (19) 对于6~8号矫平辊系,如图5所示,把第7号辊处的带材截开,以左边为平衡对象,由力矩的平衡条件可得 FP6t6-M6-M7-(FT5+FQ6)tF7=0 (20) 图5 矫平辊带材受力示意图 同理,以右边为平衡对象,可求得 (21) 7号辊的垂直力为6号辊和8号辊的垂直力之和,即 FP7= FP6+ FP8 (22) 根据式(12)、式(14)~式(22)可以得到关于入口张力FT0、水平力FQ1~FQ8和垂直力FP1~FP8的17个方程,即可求解出FT0、FQ1~FQ8和FP1~FP8。 上述方程可联立成一个非线性方程组,此方程组难以直接求解。此处采用迭代方法进行求解,如图6所示。 (1)设定水平后张力FT0的初值,可取FT0∈[0.1σsbh,0.3σsbh]; (2)计算1号辊处弯曲曲率1/ρf1、弹性极限弯曲曲率1/ρw1、残余曲率1/ r1、中性层偏移量a1、塑性弯曲力矩M1,根据式(14)、式(15)求解FQ1、FP1,求解2号辊处水平张力FT1= FT0+ FQ1; (3)按照步骤(2)依次计算2号辊~8号辊处的水平力FQi和垂直力FPi; (4)求解延伸率εa,与拉弯矫直规程设定延伸率εa0对比,如果满足收敛判据|εa-εa0|≤εw,则计算残余延伸率εr,输出FQi、FPi、εr;否则修正FT0,重新执行步骤(2)、步骤(3)直至收敛。 图6 计算框图 根据以上理论分析和计算模型,在冷轧900mm重卷机组的拉弯矫直机进行了残余延伸率试验。拉弯矫直机辊系布置如图3所示,矫直辊直径为40mm,压辊直径为350mm,辊距参数见表1。矫直带材材质为08Al,带材宽度为680mm,厚度为0.4mm,η=0.103,原始曲率半径r0=22mm。按照表2所示的矫直规程进行了试验研究,主要对比验证残余延伸率及前后张力的理论计算值与试验结果的吻合度。前后张力的试验值可以在拉弯矫直机操作台显示屏上直接读取,残余延伸率通过测量矫直前后带材长度再计算获得,即在矫直机入口处取长度L0=100mm并进行标记。矫直后,重新开卷找到标记处并测量其变形后的长度,记为L1,则可得残余延伸率εr=(L1-L0)/L0。表2所示为4种不同试验矫直规程。表3所示为残余延伸率的计算结果与试验结果。 表1 辊距 mm 表2 试验拉弯矫直规程 表3 残余延伸率计算与试验结果对比 图7为相同矫直辊压下量(表2中规程1的压下量)下,2号矫直辊设定延伸率与残余延伸率的关系曲线图,图8为设定延伸率与张力(FT0、FT8)关系的曲线图。 图7 设定延伸率与残余延伸率关系 图8 设定延伸率与前后张力关系 根据计算与试验结果(表3、表4)可知,随着矫直辊压下量的增加,前后张力减小,但残余延伸率变化不大,主要是由于随着矫直辊压下量的增加,相对张力变小,相对弯曲曲率增大,两者对残余延伸率的作用相反,使得残余延伸率变化很小。由图7、图8可知,随着设定延伸率的增加,残余延伸率及前后张力基本呈线性增大。从表3中可以看出,计算与试验误差大约在8%以内,这主要是由强化曲线按折线处理和矫直辊作用力按集中计算引起的,但误差在8%以内,说明计算模型已达到工程计算的精度。 表4 入口张力FT0、出口张力FT8计算与试验结果 kN (1)建立了拉弯矫直垂直力、水平张力、延伸率的计算模型,给出了关于垂直力、水平张力、延伸率的计算方法。 (2)由计算和试验分析可知,相同的设定延伸率下,随着矫直辊压下量的增加,前后张力减小,残余延伸率变化不大;残余延伸率及前后张力随着设定延伸率的增大而增大,与设定延伸率近似呈线性关系。 (3)计算结果与试验结果吻合良好,说明了计算模型具有较高的计算精度,能够满足工程分析的需要。 [1]连家创. 矫直理论与卷曲理论[M]. 北京:机械工业出版社, 2011. [2]任玉成, 晁春雷, 周德奇,等. 拉弯矫直重卷生产工艺研究[J]. 重型机械, 2008(3): 32-34. RenYucheng,ChaoChunlei,ZhouDeqi,etal.StudyonStretch-straighteningandRecoiling[J].HeavyMachinery, 2008(3): 32-34. [3]李淑华, 李同庆. 拉弯矫直理论和带材残余延伸率的计算[J]. 上海金属, 2001, 23(6): 30-34. LiShuhua,LiTongqing.TheoryonStretch-bendStraighteningandCalculationfortheResidualElongationofStrip[J].ShanghaiMetals, 2001, 23(6): 30-34. [4]张京诚, 窦保杰. 拉伸弯曲作用下带材挠度与弯曲曲率分析[J]. 有色金属加工, 2003,23(4): 36-38. ZhangJingcheng,DouBaojie.AnalysisofStripDeflectionandCurvatureundertheActionofTensionandBending[J].NonferrousMetalsProcessing, 2003, 23(4): 36-38. [5]张晓蓉. 拉弯矫直机故障分析及治理措施研究[D]. 重庆:重庆大学,2007. (编辑张洋) Calculation and Experimental Analysis of Stretch-bend Straightening Elongation Qi Xiangdong1,2Lian Jiachuang1,2Dong Zhikui2 1.National Engineering Research Center for Equipment and Technology of Cold Strip Rolling,Yanshan University, Qinhuangdao, Hebei, 066004 2.Yanshan University, Qinhuangdao, Hebei, 066004 At present, there was a lack of complete mathematical model in process of stretch-bend straightening. According to the calculation models of the neutral layer offset and the elongation of the strip in the process of stretch-bend straightening, the calculating methods of the tension, straightening force and elongation were given. Through calculations and industrial tests, the effects of the straightening procedure on the residual elongation were analyzed, and the accuracy of the models was verified. stretch-bend straightening; tension; elongation; calculation model; industrial test 戚向东,男,1970年生。燕山大学国家冷轧板带装备及工艺工程技术研究中心教授。主要研究方向为塑性加工工艺及装备。发表论文20余篇。连家创,男,1933年生。燕山大学机械工程学院教授。董志奎(通信作者),男,1981年生。燕山大学机械工程学院副教授。 2015-06-23 TG333.2 10.3969/j.issn.1004-132X.2016.08.021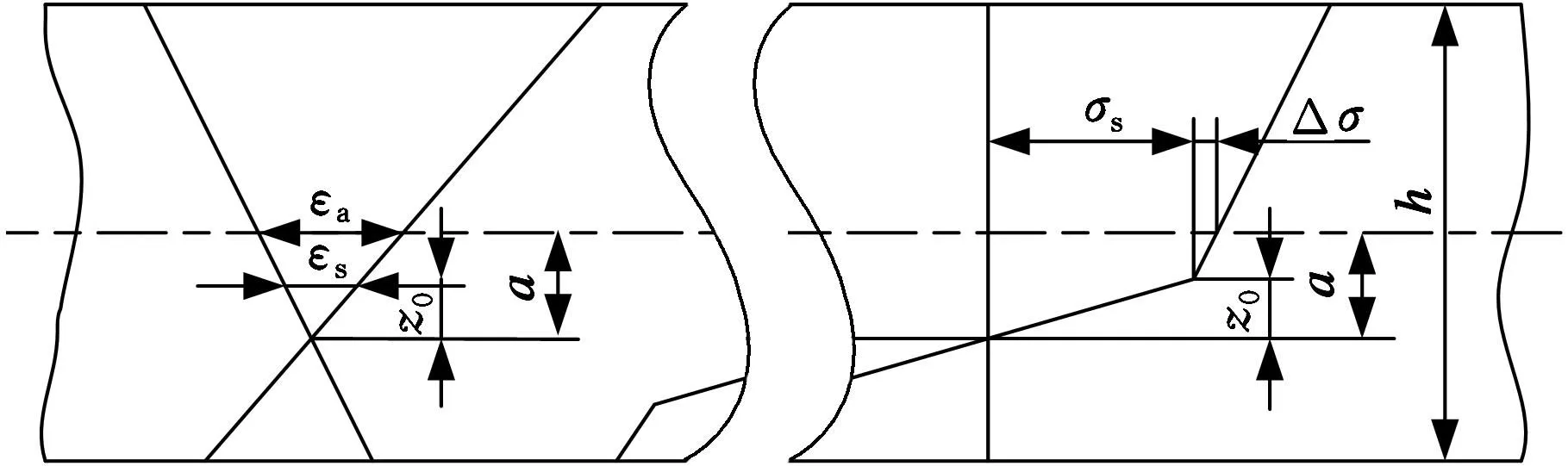
3 拉弯矫直张力的计算


4 残余延伸率的计算方法
5 计算及试验分析




6 结论
