两移动三转动混联机构型综合

秦友蕾　曹　毅　陈　海

1.江南大学，无锡，214122　　2.上海交通大学机械系统与振动国家重点实验室，上海，2002403.江苏省食品先进制造装备技术重点实验室，无锡，214122



两移动三转动混联机构型综合

秦友蕾1,3曹毅1, 2, 3陈海1,3

1.江南大学，无锡，2141222.上海交通大学机械系统与振动国家重点实验室，上海，2002403.江苏省食品先进制造装备技术重点实验室，无锡，214122

基于GF集理论提出一种系统有效的串联、并联混联机构型综合方法。首先介绍GF集的基本概念、运算法则，以及转动特征存在条件。然后通过分析混联机构结构的组成特点，基于GF集元素组合和转动轴线迁移定理，提出了设计混联机构型综合方法，根据机构的拓扑结构和结构参数之间的关系，建立了混联机构数综合方程，给出了混联机构型综合的具体步骤。之后根据混联机构型综合理论，完成了具有2T3R混联机构运动特征的构型设计，得到了大量新构型。最后，针对综合出的一种2T3R混联机构，通过混联机构末端分析方法，验证了所设计出混联机构的运动特征，从而证明了构型综合方法的正确性。

混联机构；GF集；构型综合；并联机构

0　引言

20世纪90年代，Neumann博士提出了Tricept混联机器人的概念，这类机器人机构结合了串联机构操作空间大、控制灵活，并联机构刚性好、动态性能好、精度高的优点，同时规避了单纯串联、并联机器人的问题，成为机构学研究的一个重要发展方向，同时也拓宽了机器人的应用领域，广泛应用于食品包装、医疗设备、电子封装、坐标划线机领域。例如ABB公司基于Tricept机构设计了IRB940混联机器人；李彬等[1]发明了多种新型五自由度TriVariant、EXE-M和Tricept-IV等系列混联机器人，可广泛用于焊接、切割、喷涂、高速加工和装配等操作。

目前，混联机器人的研究已取得了一定的成果但仍处于起步阶段，众多学者对混联机器人的研究主要集中在混联机构建模及运动学和动力学分析[2-5]，而缺少一种简单而系统有效的混联机器人构型综合方法[6-8]。机构型综合是机器人机构设计中最重要的环节，机构拓扑创新是机械发明最具挑战性的核心内容[9]。因此混联机构设计方法的研究，具有重要的理论意义[6]。

本文针对当前混联机器人机构结构创新设计的瓶颈问题，将GF集构型理论应用于混联机器人机构设计之中，提出一种系统有效的混联机器人机构型综合方法。并以此理论完成了对两移动三转动混联机器人构型综合。

1　GF集理论

1.1GF集的基本概念

称描述机器人机构末端运动特征的集合为GF集。GF集由6个元素构成：

GF={Ta，Tb，Tc；Rα，Rβ，Rγ}

(1)

其中，Ti描述了机器人末端移动特征，i=a，b，c；Rj描述了机器人转动特征，j=α，β，γ。

GF集中移动特征Ti的3个移动方向如图1表示，转动特征Rj的3个转动轴线方向如图2表示。GF集中的6个元素互相独立，当机构具有某运动特征时，GF集中的对应值不为0，反之，为0[9-10]。

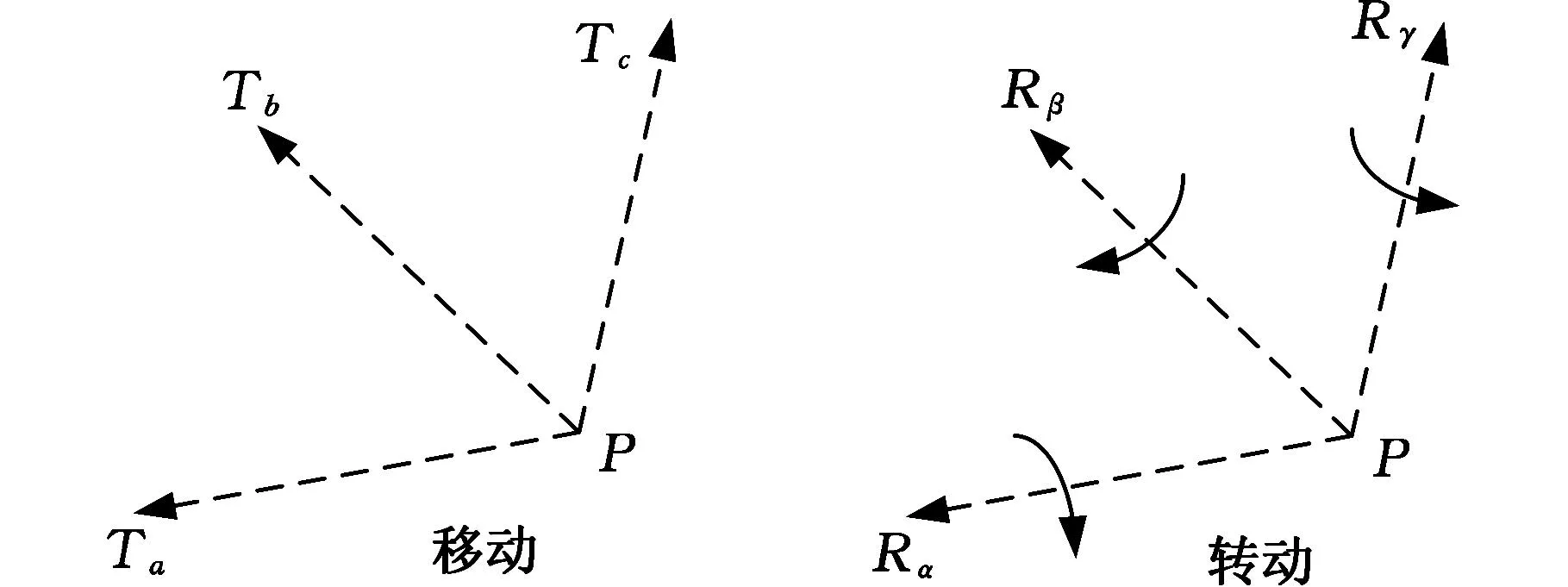
图1　GF移动的描述　　　图2　GF转动的描述

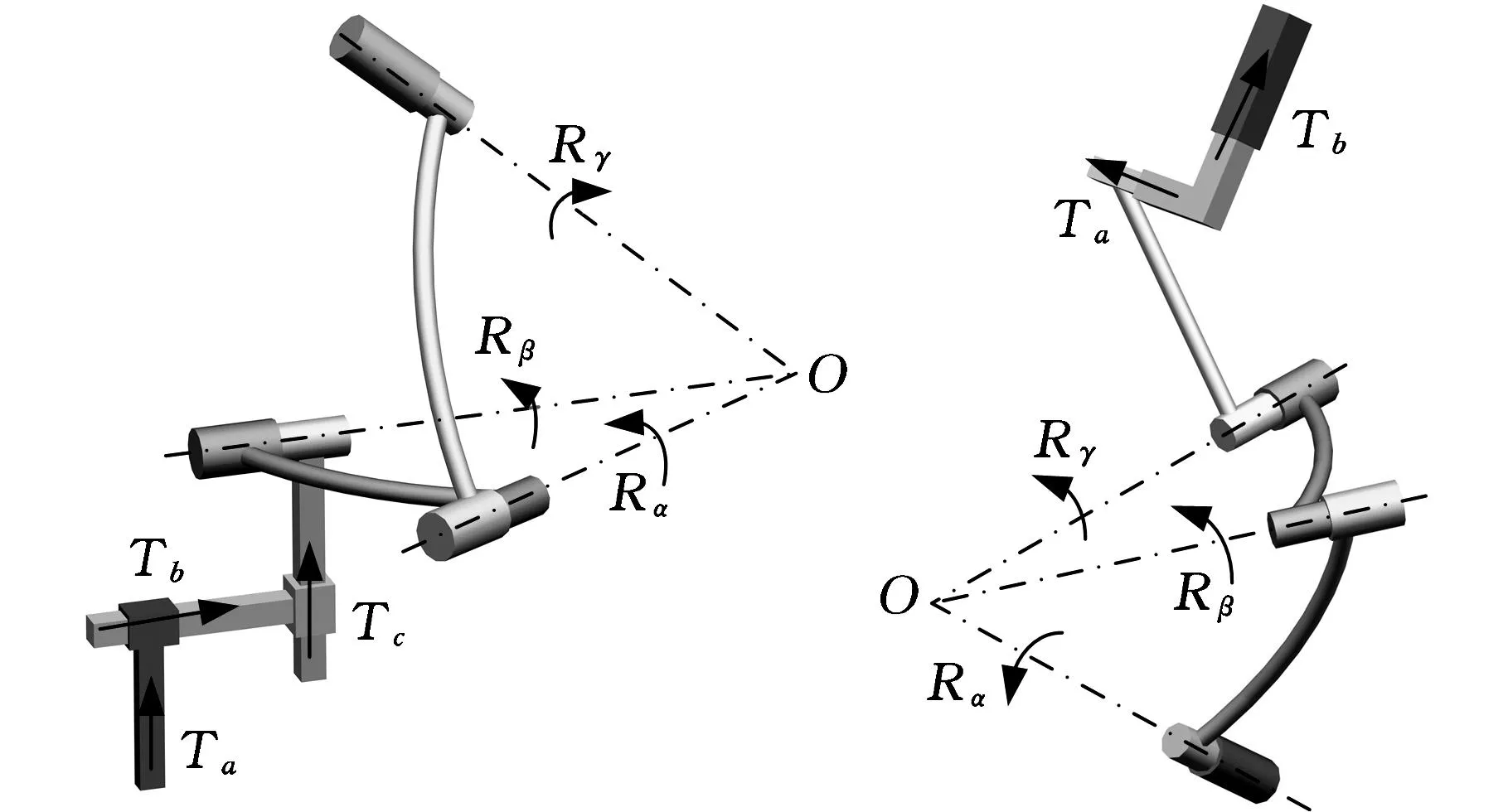
图3　第一类图4　第二类

1.2运算法则

串联机器人末端的运动特征是组成该串联支链运动副的特征的总和，即GF集求和运算，具体定义为

GF=GF1∪GF2={Ta，Tb，Tc；Rα，Rβ，Rγ}

(2)

GF1={A；B}=(Ta1，Tb1，Tc1；Rα1，Rβ1，Rγ1)

GF2={C；D}=(Ta2，Tb2，Tc2；Rα2，Rβ2，Rγ2)

式中，“+”为Ti对Rj的影响运算符，主要依据转动轴线迁移定理[9]；T(•)为运动项的移动特征部分；R(•)为运动项的转动特征部分。

求交运算具体定义为

GF=GF1∩GF2={Ta，Tb，Tc;Rα，Rβ，Rγ}

(3)

转动特征相比于移动特征而言，判定比较困难，其判定需遵循转动合成定理，如图5所示，刚体上任意两点A0、B0，当刚体绕A0点旋转时，点B0到达B点。由坐标变换位移矩阵可知：

(4)

式中，A0、B0分别为刚体上A、B两点起始位置；A、B变化后的位置；Rα,β,γ为刚体绕A点的三维转动变换矩阵。

图5　两点间三维相对转动的关系

图5中，vA、vB分别为A、B两点的速度，由式(4)可知，vB不但具有与vA相同的转动速度而且B点存在绕A点时产生的三维伴随移动速度,即

(5)

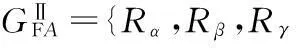
同理可知，当Rα,β,γ变为二维转动变化矩阵Rα,β及一维转动变化矩阵Rα时，可得出转动特征合成定律：当一个刚体绕点A旋转时，固定在刚体上的点B除了具有与点A相同的转动，还具有绕点A转动产生的伴随移动。

2　基于GF集的混联机构构型综合理论

2.1混联机构型综合方法

机器人机构的型综合是指确定机构的构件数目、运动副数目及其类型，以及可能的连接方式，以获得确定符合要求的所有机构。目前国内外主要有5种机构型综合方法，即基于螺旋理论的约束综合法[11]、基于微分几何理论的群论法[12]、机构型综合的图论方法[13]、基于线性变换的型综合方法[14]、基于POC单元的运动综合方法[15]。

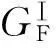
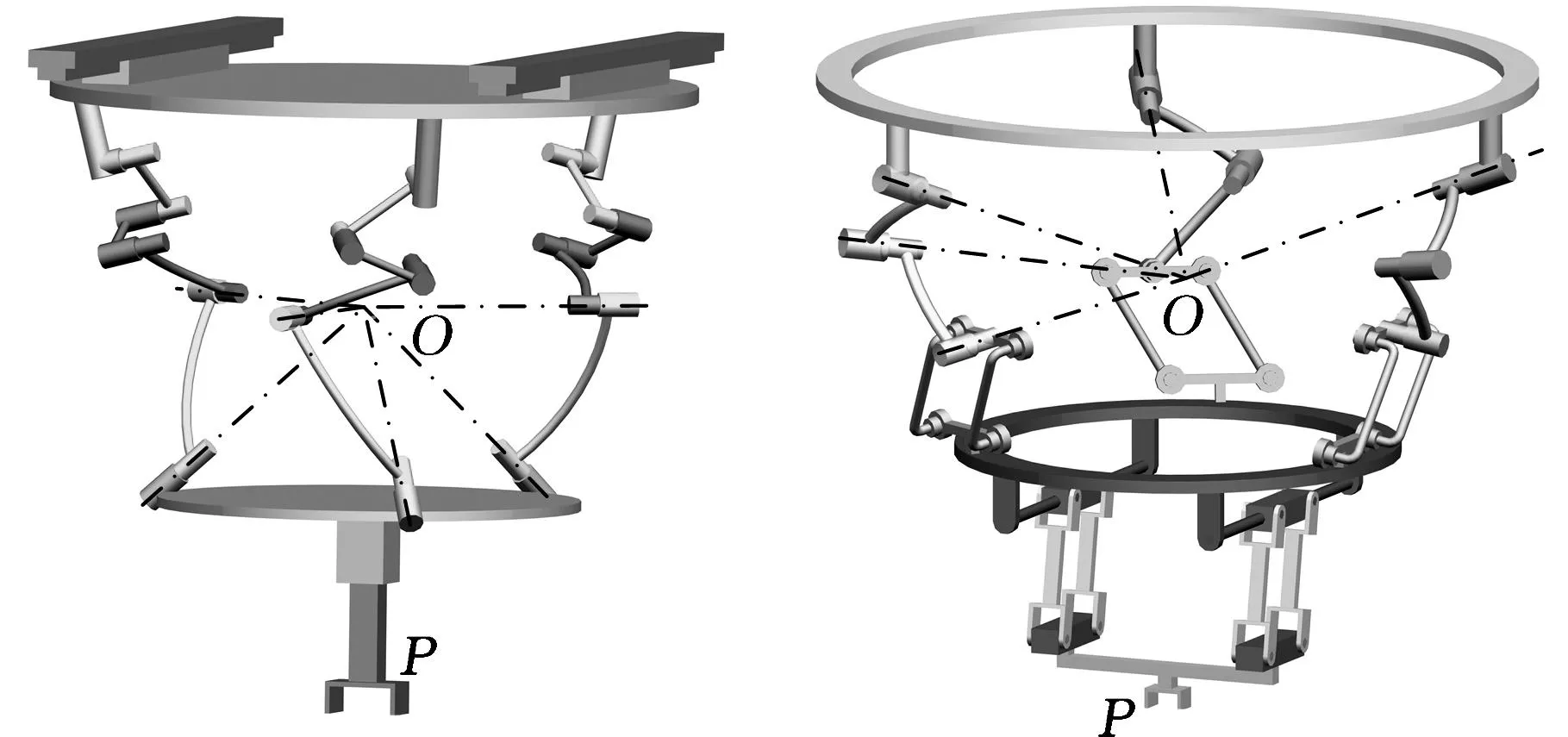
图混联机构　　　　图混联机构

混联机构是将串联与并联机构按照一定方式组合而成的至少具有三自由度的拓扑结构。构型方法与串、并联机构相类似，可参考目前国内外研究机构的构型理论，基于GF集可知混联机构的运动特征是所有构成该机构的串联支链以及并联模块运动特征的和集，即

GF=GFS1∪GFS2∪…∪GFSn∪GFP1∪…∪

GFPj∪GFS(n+1)∪…∪GFSi

(6)

式中，GF为机构的运动特征；GFSi为串联形式运动特征；GFPj为并联机构运动特征。

由式(6)可知，要综合出给定末端运动特征的混联机构，需找到特定并联模块以及串联支链，同时要按照一定的顺序将它们连接到一起。混联机器人驱动器可以布置在不同的支链上，同时机构还可能存在被动支链，因此有必要建立机构的拓扑结构和结构参数之间关系的模型，即混联机构数综合方程：

(7)

式中，F、Fp、Fs分别为混联、并联、串联特征GF集的维数；qi为主动支链i上的驱动副数；N为支链数；n为驱动副数；p为被动支链数。

2.2混联机构GF元素组合原则

当混联机构运动特征中含有转动特征元素时，GFSi和GFPj中元素的排列位置和顺序与混联机构末端特征密切相关，确定转动轴线的位置至关重要，因此有必要研究GF集中元素排列位置和顺序对混联机构末端转动特征的影响规律。

为了使创新出来的方案更加合理，在此给出了混联机构结构方案合理性原则：

(1)对称性结构具有易于控制、制造和装配简单等优点，考虑到混联机构在实际运用过程中的需要，因此，混联机构中的并联模块尽量为对称结构。

(2)考虑结构刚性较强以及设计简单的要求，混联机构并联模块中的被动支链数p=0，且各主动链中驱动数qi=1。

(3)GF元素组合时必须遵循混联机构转动轴线迁移定理。

2.3混联机器人构型综合步骤

根据上述设计方法和原则，得到构型步骤如下：

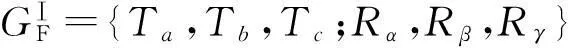
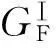
(3)根据并联机构GF集表达式GFPj，综合考虑并联机构的对称性，按照式(3)、式(7)构造满足要求的并联机构。

(4)根据串联机构GF集的表达式GFSi，按照式(2)构造满足要求的串联机构。

(5)将从步骤(3)、步骤(4)得到的并联机构GFPj及串联机构GFSi，按式(5)串、并模块单元的顺序及混联机构转动轴线迁移定理组合成混联机构。

上述构型步骤，可用图8所示流程表示。

图8　混联机器人构型综合流程图

3　2T3R类混联机构型综合方法

运用上述构型综合方法和步骤对2T3R五自由度混联机构进行构型综合，其末端的GF集表达式为

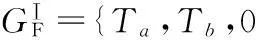
(8)

(9)

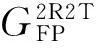
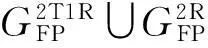
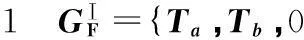
表；Rα，Rβ，Rγ}的组合方式

表的组合方式

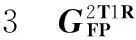
表型对称并联机构类型

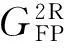
表型部分并联支链构型

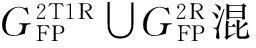
图9　3(PPaR)plR&[PU&(PaRR)plR]混联机构

4　实例分析

构型设计是已知运动求解机构的拓扑结构，而机构分析却恰恰相反，为分析机构末端的自由度，很多学者提出了自己的方法和公式，发展了诸如基于Grubler-Kutzbach(G-K)公式计算法[9]、群论和李代数法[12]、反螺旋理论[11]、POC法[15]。但是上述方法大多缺乏通用性且主要针对的是并联机构，而很少有关于对混联机构自由度的研究。

基于GF集的混联机构型综合逆过程，可分析出混联机器人机构末端的运动特征，其基本思路为：首先分析混联机构的构造方式，确定机构中的并联模块和串联模块；之后对组成并联模块的分支的GF集进行求交运算，得到并联模块的GF集，然后对组成串联模块的运动副GF集进行求和运算，得到串联模块的GF集；最后将多个模块GF集进行求和运算，求得的和集为混联机构的末端运动特征。

下面以图9所示的3(PPaR)plR&[PU&(PaRR)plR]混联机构为例，使用基于GF集的混联机构末端特征分析方法对该混联机器人机构进行分析。

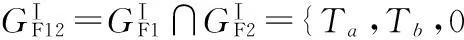
(10)

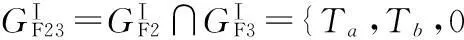
(11)

{Ta，Tb，0；Rα，0，0}

(12)

图10　(PaRR)plR支链　　　　图11　PU支链

由图12可知Rγ4⊥αTb4Tc4，其中，αTa4Tb4是Ta4、Tb4所在平面。由图9可知，Rγ3⊥αTb4Tc4且PU支链中的转动副轴线Rβ3与支链(PaRR)plR中的转动副轴线Rβ4共轴。由式(3)可知第二个并联机构末端运动特征：

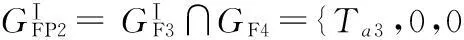
{0，Tb4，Tc4；0，Rβ4，Rγ4}={0，0，0；0，Rβ3，Rγ3}

(13)

根据式(6)以及轴线迁移定理可得

{0，0，0；0，Rβ3，Rγ3}={Ta，Tb，0；Rα，Rβ3，Rγ3}

(14)

由以上分析可知，3(PPaR)plR&[PU&(PaRR)plR]混联机器人的末端GF={Ta，Tb，0；Rα，Rβ3，Rγ3}。

图12　(PaRR)plR支链

5　结论

(1)本文基于GF集构型理论，提出一种混联机器人机构型综合理论以及求解混联机构末端运动特征的方法。

(2)将混联机构分成两类，给出了混联机构型综合的具体算法、设计步骤，建立了混联机构数综合方程。

(3)根据混联机构型综合方法综合到了2T3R五自由度混联机构，针对综合出的3(PPaR)plR&[PU&(PaRR)plR]混联机构，运用混联机构末端分析方法求得了该机构的运动特征，从而验证了构型理论的有效性。

(4)该综合方法可用于具有确定运动特征的串联、并联以及混联机构的构型设计，对机构型综合具有一定的指导作用。

[1]李彬，黄田，刘海涛，等．Exechon 混联机器人三自由度并联机构模块位置分析[J]. 中国机械工程，2010，21(23):2785-2789.

Li Bin, Huang Tian, Liu Haitao, et al. Position Analysis of a 3-DOF PKM Module for a 5-DOF Hybrid Robot Exechon[J]. China Mechanical Engineering, 2010, 21(23): 2785-2789.

[2]Pisla D, Gherman B, Vaidan C, et al. An Active Hybrid Parallel Robot for Minimally Invasive Surgery[J]. Robotics and Computer-Integrated Manufacturing, 2013, 29(4): 203-221.

[3]Huang Tian, Wang Panfeng, Zhao Xueman. Design of a 4-DOF Hybrid PKM Module for Large Structural Component Assembly[J]. CIRP Aunals Manufacturing Technology, 2010,59(1):159-162.

[4]Joubair A, Zhao L, Bigras P, et al. Absolute Accuracy Analysis and Improvement of a Hybrid 6-DoF Medical Robot[J]. Industrial Robot, 2015, 42(1):101-113.

[5]Hu Bo. Complete Kinematics of a Serial-parallel Manipulator Formed by Two Tricept Parallel Manipulators Connected in Serials[J]. Nonlinear Dynamics，2014(4)2685-2698.

[6]Alexandre C, Christoph B, Jurgen H. A Type Synthesis Method for Hybrid Robot Structures[J]. Mechanism and Machine Theory,2008, 43(8)：984-995.

[7]Shen Huiping，Zhao Haibin，Deng Jiaming，et al. Type Design Method and the Application for Hybrid Robot Based on Freedom Distribution and Position and Orientation Characteristic Set[J]. Chinese Journal of Mechanical Engineering, 2011,47(23):56-64.

[8]Zeng Qiang, Fang Yuefa. Structural Synthesis and Analysis of Serial-parallel Hybrid Mechanisms with Spatial Multi-loop Kinematic Chains[J]. Mechanism and Machine Theory, 2012,49(3):19-215.

[9]高峰,杨加伦, 葛巧德. 并联机器人型综合的GF集理论[M]. 北京: 科学出版社, 2011.

[10]Yang Jialun, Gao Feng, Ge Q J, et al. Type Synthesis of Parallel Mechanisms Having the First Class GFSets and One-dimensional Rotation[J]. Robotica, 2011, 29(6): 895-902.

[11]Huang Zhen, Li Qinchuan. General Methodology for Type Synthesis of Lower-mobility Symmetrical Parallel Manipulators and Several Novel Manipulators[J]. International Journal of Robotics Research, 2002, 21(2):131-145.

[12]Li Qinchuan, Huang Zhen, Hervé J M. Displacement Manifold Method for Synthesis of Lower-mobility Parallel Mechanisms[J]. Science in China Series E: Technological Sciences, 2004,47(6): 641-650.

[13]Lu Y，Ding L，Yu J. Autoderivation of Topological Graphs for Type Synthesis of Planar 3DOF Parallel Mechanisms[J]. Journal of Mechanisms and Robotics, 2009,2(1):298-320.

[14]Gogu G. Structural Synthesis of Maximally Regular T3R2-type Parallel Robots via Theory of Linear Transformations and Evolutionary Morphology[J]. Robotica, 2009,27(1):79-101.

[15]Yang Tingli, Liu Anxin, Jin Qiong, et al. Position and Orientation Characteristic Equation for Topological Design of Robot Mechanisms[J]. Journal of Mechanical Design, 2009,131(2):021001-0210012.

(编辑张洋)

Type Synthesis of Two-translational and Three-rotational Hybrid Mechanisms

Qin Youlei1,3Cao Yi1,2,3Chen Hai1,3

1. Jiangnan University, Wuxi, Jiangsu,214122 2. State Key Laboratory of Mechanical System and Vibration, Shanghai Jiao Tong University,Shanghai, 200240 3. Jiangsu Key Laboratory of Advanced Food Manufacturing Equipment and Technology,Wuxi, Jiangsu, 214122

A systematic and effective type synthesis method which was suit for serial and parallel as well as hybrid mechanism was proposed based onGFset. The basic concept ofGFset, algorithms and the type synthesis principles, requirements for rotation were introduced based onGFset firstly. Secondly, an approach to synthesize of hybrid mechanism was presented by analyzing the characteristics of structure composition. The topological arrangements of hybrid mechanisms might be developed by the elements ofGFset combination and rotation axis transfer theorem. According to the relationships among dimensions of end-effector characteristics and structural parameters of mechanisms the number synthesis formulas was set up. Specific process for structural synthesis of HMs was finished. Simultaneously, a lot of new mechanisms were attained. According to the proposed approach, 2T3R 5-DOF hybrid mechanism with determined kinematic characteristic was enumerated. Meanwhile, a method was proposed to analyze kinematic characteristic of hybrid mechanisms synthesized above. Finally, a novel hybrid mechanism was synthesized to demonstrate the applicability of the novel method of structural synthesis for hybrid mechanisms.

hybrid mechanism(HM);GFset; type synthesis; parallel mechanism

秦友蕾，男，1991年生。江南大学机械工程学院硕士研究生。主要研究方向为机器人机构学。曹毅，男，1974年生。江南大学机械工程学院副教授。陈海，男，1991年生。江南大学机械工程学院硕士研究生。

2015-05-28

国家自然科学基金资助项目(50905075);机械系统与振动国家重点实验室开放课题资助项目(MSV201407);江苏省食品先进制造装备技术重点实验室开放课题资助项目(FM-201402);江苏省普通高校学术学位研究生科研创新计划项目资助项目(KYLX-1115)

TH112

10.3969/j.issn.1004-132X.2016.08.002