基于横观各向同性假定的固定结合部本构关系及有限元模型

赵金娟　王世军　杨　超　王诗义　杨慧新

西安理工大学，西安，710048



基于横观各向同性假定的固定结合部本构关系及有限元模型

赵金娟王世军杨超王诗义杨慧新

西安理工大学，西安，710048

提出了一种固定结合部的有限元建模方法。该方法将接触层等效成均质、虚拟的横观各向同性材料。根据结合面的变形和载荷关系，推导了虚拟材料本构矩阵中5个独立变量与法向应力之间的非线性关系。将这个本构关系引入到有限元分析中用以建立机器的固定联接面模型。分析结果与试验结果的对比证实了该方法的有效性。

固定连接；虚拟材料；有限元；本构关系

0　引言

结合面对结构的静态和动态特性有显著的影响。通常认为机床中有30%～50%的刚度、90%的阻尼来自于结合面[1]。机械结合面的建模是机械结构整机性能分析的关键[2-5]。

在基于有限元法的机械结构整机性能分析中，结合面主要采用弹簧-阻尼单元建模[6]。使用这种单元需要根据单元附属的接触面积求得单元的刚度和阻尼。如果接触表面的实体单元网格不规则，则每一个弹簧-阻尼单元的附属面积都需要单独计算，工作量很大。在有限元软件中，这种节点对节点的弹簧-阻尼单元不能像实体单元那样自动生成，需要手工操作，逐个生成，过程比较繁琐。此外，这种单元相互之间没有耦合关系，不能反映结合面相邻区域之间的影响。

地质力学中，如果岩石的节理和结构之间的土壤层非常厚，在有限元分析时可以使用等参的薄层实体单元建模。这种单元的优点是在有限元软件中可以自动生成，也不需要计算弹簧-阻尼单元的附属面积，但是在机械结构的固定连接面中，接触层的厚度并不确定，很难利用这种单元建立机械结合面模型[7-12]。

文献[13]给出了一种利用薄层单元建立结合面模型的方法，文中假定薄层单元的厚度接近于0，结合面被看作一种虚拟的正交各向异性材料并且给出了这种虚拟材料的正交各向异性的本构矩阵：

[σxxσyyσzzσxyσyzσzx]T=

diag(0，0，E33，0，G，G) [εxxεyyεzzεxyεyzεzx]T

(1)

这里的E33是虚拟材料沿结合面法线方向的弹性模量，G是虚拟材料的剪切模量。在这个对角形式的本构关系中，有3个对角元素等于0，这使得矩阵是奇异的。材料力学中，材料本构矩阵的对角元素必须大于零[14]，因此式(1)的本构关系并不能直接用于结合面的建模。此外，接近于0的厚度在结合面几何建模时也很难操作。

本文提出了一种基于虚拟材料的具有有限厚度的固定结合面建模方法。该方法将结合面及其附近区域等效成均匀的横观各向同性区域并用八节点的六面体实体单元模拟。接触层的实体单元可以在有限元软件中自动生成，不需要计算单元的附属面积，同时实体单元也能很好地反映结合面相邻区域的相互作用。

1　虚拟材料的本构关系和接触单元的刚度矩阵

如果材料在平行于名义接触平面oxy的方向上具有相同的机械性质，则有下面的应变-应力关系[14]：

(2)

式中，Ex、Ey、Ez分别为x、y、z方向上的弹性模量；μij为单独在j方向作用正应力σj而无其他应力分量时，i方向应变与j方向应变之比的负值，即泊松比，i, j=x, y, z; Gxy、Gyz为Gxz剪切模量，下标的第一个字母表示法线方向，第二个字母表示剪切变形的方向。

式(2)是一个包含独立参数Ex、Ez、μxy、μxz和Gxz的横观各向同性材料的本构方程。

图1a所示的包含接触界面的矩形微体中，接触层平行于oxy平面。假定微体的厚度dz远大于接触层的厚度，外表面受到均布的法向和切向载荷。根据微体的应变-应力关系，可以求得图1b所示的虚拟弹性体(与图1a中微体等效、均一的横观各向同性的虚拟弹性体)的5个独立参数。

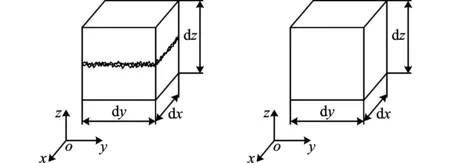
(a)微体　　　　　　(b)虚拟弹性体图1　包含接触层的微体和等效的虚拟弹性体

1.1弹性模量Ex

图1a中，在微体表面施加x方向的法向载荷σx，x方向产生应变εx。微体的厚度比接触层的真实厚度大很多，可以认为图1a中包含结合面的微体的应变εx等于图1b中不包含结合面的微体的应变εx，接触层的存在与否，并不影响σx与εx之间的关系。σx与εx仍然保持基体材料的应力-应变关系。图1b中,虚拟弹性体的弹性模量Ex等于基体材料的弹性模量E。

1.2弹性模量Ez

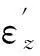
(3)

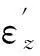
(4)

由于无法确定准确的接触层厚度，所以接触层的应变ε″z也无法计算。本文按下式定义接触层的应变：

ε″z=λn/dz

(5)

其中，λn为接触层在法向载荷σz下的法向变形，λn-σz的关系可以通过试验或者理论分析获得。根据这个定义，接触层的应变与微体的厚度dz相关。随着微体厚度的变化，接触层的应变ε″z也随着改变。试验研究已经显示接触层的法向变形是法向载荷的幂函数[15-16]：

(6)

其中，c和m是系数，可通过拟合试验数据确定。因此，接触层的应变ε″z可用写成下面的形式：

(7)

在施加法向载荷σz后，微体将产生如下的法向应变：

(8)

由于

σz=Ezεz

(9)

所以微体在z方向的弹性模量

(10)

1.3泊松比μxy

泊松比μxy反映了x方向法向应变εx与y方向法向应变εy之间的耦合关系。本文认为μxy与基体材料的泊松比μ相同：

μxy=μ

(11)

1.4泊松比μxz

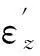
(12)

(13)

(14)

接触层的应变ε″z与式(5)、式(7) 相同：

(15)

这样，虚拟材料的泊松比

(16)

1.5剪切模量Gxz

Gxz是虚拟弹性体在oxz平面内的剪切模量。图1中的微体被假定是横观各向同性的，微体在oxz面内的剪切刚度与oyz面内的剪切刚度相等：

Gxz=Gyz

(17)

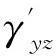
(18)

不包含接触层时，微体在x方向的剪应变

(19)

接触层的剪应变

γ″xz=λxz/dz

(20)

其中，λxz是接触层在x方向的剪切变形。类似于接触层的法向变形λn，λxz也能够从结合面试验获得：

(21)

其中，ατ、βτ都是与法向载荷σz相关的系数，与式(7)中的c和m类似。根据式(18)～式(21)，可以得到

(22)

即

(23)

这样，oxz面内的剪切模量

(24)

最终，如果通过试验获得c、m、ατ、βτ，就可以求得虚拟材料的5个独立变量：

(25)

1.6接触单元的刚度矩阵

有限元分析中，八节点的三维实体等参元是一种经常使用的实体单元，大多数商业软件也提供这种单元，它的刚度矩阵为[17]

(26)

式中，B、D、J分别为应变矩阵、弹性矩阵和雅可比行列式；wξ,i、wη,j、wζ,k为高斯积分的权系数。

由于式(2)中的系数矩阵的逆即为弹性矩阵D，根据结合面的试验数据，就可以得到虚拟材料的弹性矩阵。将这个弹性矩阵代入式(26)，即可得到薄层单元的刚度矩阵。接触单元的形状不同于通常的三维实体单元，单元的2个表面必须平行于名义的接触界面，以便保持单元厚度的一致。接触层的真实厚度非常小，采用太厚的接触单元会显著改变零件中的应力分布。在前述5个独立变量的分析中，假定微体的厚度必须远大于真实接触层的厚度，因此接触单元的厚度也必须远大于真实接触层的厚度。在微体的应变分析中，所有的应变都假定是小应变。在接触层变形相同的条件下，单元厚度越小，单元的应变越大，这使得单元的厚度不能太小。文献[12]认为等参单元的边长比超过1000也不会产生显著的数值误差，因而这种等参元用作薄层单元模拟接触层的性质是可行的。

2　本构关系和接触单元的试验验证

文献[18]通过试验研究了结合面切向变形与切向载荷的关系。试验结果显示，结合面出现宏观滑动之前，经历了弹性变形、塑性变形和微滑移三个阶段。结合面只在弹性变形阶段才表现出线性的切向刚度。在弹塑性过渡阶段和微滑移阶段，结合面表现出非线性的切向刚度。图2为文献[18]中试验装置的示意图。2个100 mm×50 mm×18 mm的钢制磨削试样之间的接触面为研究的结合面。结合面的法向载荷是试样A的自重以及上面的配重。试样B固定在基础梁上，基础梁通过减振器固定在工作台上，这样能够隔绝来自地面的振动。结合面的切向载荷施加在试样A的两侧并且载荷作用点靠近结合面以避免在结合面上产生力矩。

图2　切向变形的试验装置

结合面的切向变形通过2个分辨率为12.5 nm的电容传感器测量。如图2所示，传感器SB放在试样B的一端，测量试样B的切向位移，传感器SA用来测量试样A的切向位移。如果接触层的法向应力和切向应力是均匀的，那么2个传感器测量结果的差值就是接触层的切向变形。

试验装置的有限元模型包含1008个单元，其中，144个单元是本文提出的接触单元。这个模型中，接触层的厚度是100 μm，由一层矩形六面体接触单元划分而成。与图2相同，试样B的下表面被固定，20 kPa的压力施加在试样A的上表面，每侧的切向力是3 N。试样的材料参数如下：弹性模量E=200 GPa，泊松比μ=0.3，密度ρ=7850 kg/m3。接触层的试验数据采用文献[16]中的数据：

(27)

其中，pn(pn≤2.5 MPa)为结合面的法向压力，相当于式(25)中的σz；knj、ktj分别为结合面单位面积上的法向刚度和切向刚度，对照式(6)和式(21)可知

(28)

式(28)与式(27)在形式上相同，对照两式即可确定参数c、m、ατ、βτ，进而可以确定式(25)中虚拟材料的5个独立变量。

式(25)中，有些材料参数与接触层的法向载荷之间是非线性关系，这使得有限元模型是非线性的。如果接触单元的法向应力不一样，则接触单元的材料参数也不一样。计算时，首先施加法向压力pn，当法向压力pn增加到20 kPa时，开始施加切向载荷pt。计算获得的剪切变形与剪切载荷之间的关系显示在图3中。作为比较，文献[18]的试验结果也显示在图3中。对比两条曲线可以发现，计算结果与试验结果是一致的。文献[18]的试验中，法向载荷只有20 kPa，当切向载荷pt超过4.7 kPa时，切向变形开始进入塑性变形阶段并出现明显的宏观滑移；切向载荷小于4.7 kPa时，宏观滑移较小，切向变形与切向载荷大体呈线性关系，但是比计算结果略大。式(27)适用于最大法向载荷为2.5 MPa的情况，远大于文献[18]中20 kPa的法向载荷，式(27)的适用条件与文献[18]中的试验条件并不完全相同。由于结合面的非线性性质[1]，在切向载荷相同的条件下，法向载荷大的结合面，其切向刚度也大。因此图3中切向变形的试验结果比计算结果略大是合理的。

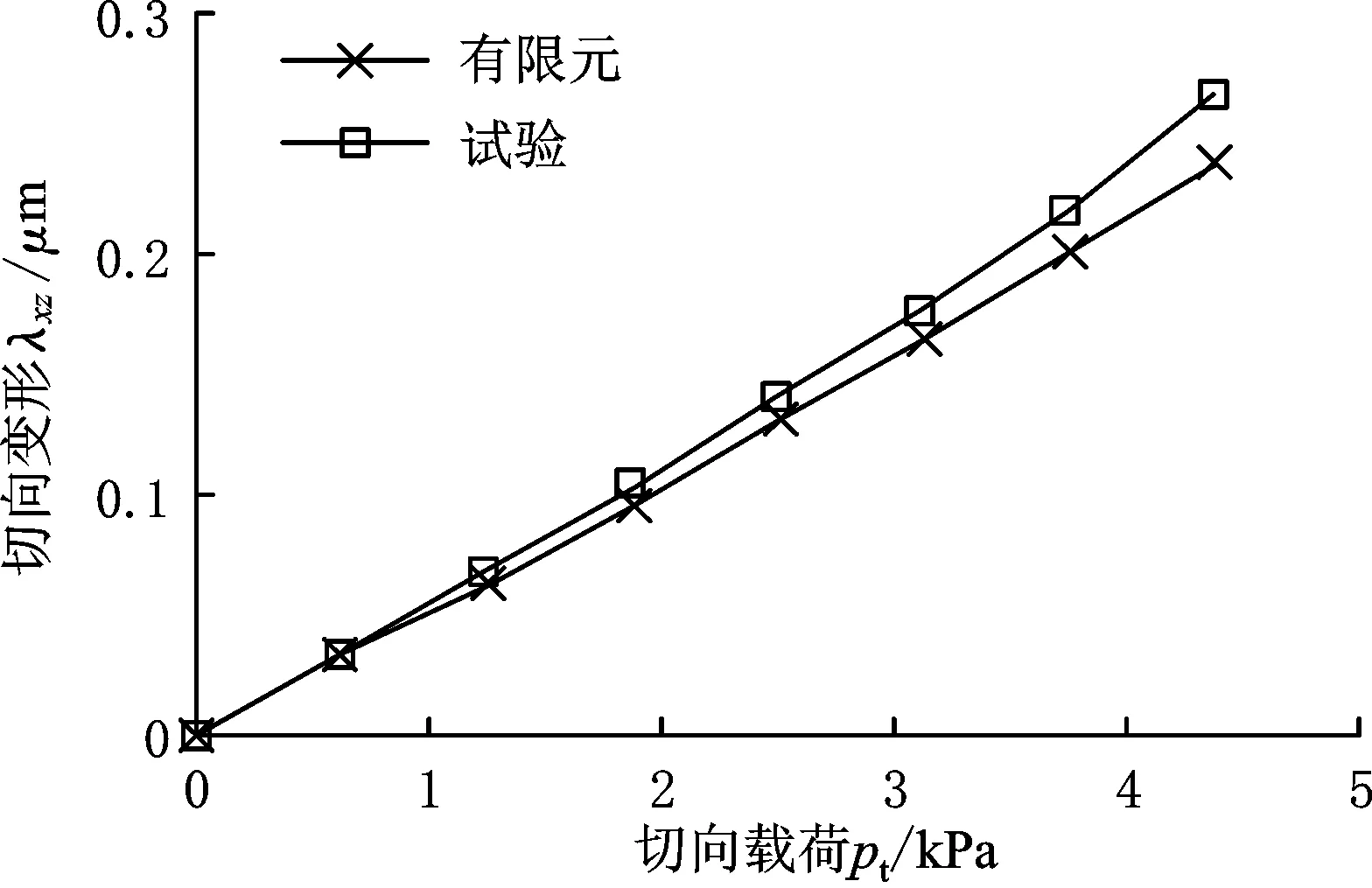
图3　切向变形的试验结果和有限元结果比较

当法向压力pn=20 kPa，切向载荷pt=4.7 kPa时，接触层沿x方向的剪切应力如图4所示。图4中，接触层的剪切应力分布不均匀，应力变化达到9.5%，这使得接触层的剪切变形也不一致。出现这种现象的原因在于切向载荷不是均匀施加在接触层上的。这种不一致的剪切变形，使得传感器A和B的测量结果不能够准确地反映接触层的切向变形，这也是结合部切向特性的试验研究中的主要困难之一。

图4　接触层x方向的剪应力分布

3　结语

本文提出的利用等参实体单元建立固定结合面模型的方法中，结合面被等效为一个虚拟的横观各向同性实体，实体单元的材料特性通过结合面的试验结果获得。常用的有限元软件都有本文方法所使用的材料本构关系和单元类型，因此本文的方法能够方便地应用在多数商业性的有限元软件中。实体单元可以通过软件快速自动生成，从而给结合面的有限元建模带来便利。

本文采用试验获得的结合面变形-载荷关系建立了虚拟材料的本构矩阵。事实上，本构关系的建立也可以利用其他方法获得的结合面的变形-载荷关系，例如基于粗糙表面轮廓的有限元分析，分形接触理论以及统计接触理论等，本文提出的结合面建模方法具有通用性。

[1]赵宏林, 丁庆新, 曾鸣，等. 机床结合部特性的理论解析及应用[J]. 机械工程学报, 2008, 44(12):208-213.

ZhaoHonglin,DingQingxin,ZengMing,etal.TheoreticAnalysisonandApplicationofBehaviorsofMachineToolJoints[J].JournalofMechanicalEngineering, 2008, 44(12): 208-213.

[2]石坤, 宋俐, 师俊平. 机械结合部等效材料参数建立与试验[J]. 农业机械学报, 2014, 44(6): 297-301.

ShiKun,SongLi,ShiJunping.EstablishmentandExperimentofMechanicalJointEquivalentMaterialProperties[J].TransactionsoftheChineseSocietyforAgriculturalMachinery, 2014, 44(6): 297-301.

[3]黎定仕, 张以都, 王鹏. 基于结构阻尼的机械结合部动力学模型研究[J]. 振动与冲击, 2010, 29(8): 204-208.

LiDingshi,ZhangYidu，WangPeng.DynamicModelofMachineJointsBasedonStructuralDamping[J].JournalofVibrationandShock, 2010, 29(8): 204-208.

[4]米良, 殷国富, 孙明楠, 等. 结合部动力学特性的立柱-主轴系统动力学模型研究[J]. 农业机械学报, 2011, 42(12): 202-207.

MiLiang,YinGuofu,SunMingnan,etal.ColumnspindleSystemDynamicModelBasedonDynamicCharacteristicsofJoints[J].TransactionsoftheChineseSocietyforAgriculturalMachinery, 2011, 42(12):202-207.

[5]刘恒, 刘意, 王为民. 接触界面法向刚度等效的新方法[J]. 机械工程学报, 2011, 47(17): 37-43.LiuHeng,LiuYi,WangWeimin.NewEquivalentMethodforNormalStiffnessofContactInterface[J].JournalofMechanicalEngineering, 2011, 47(17): 37-43.

[6]TianHongliang,LiBin,LiuHongqi,etal.ANewMethodofVirtualMaterialHypothesis-basedDynamicModelingonFixedJointInterfaceinMachineTools[J].InternationalJournalofMachineTools&Manufacture, 2011, 51: 239-249.

[7]AhmadianH,EbrahimiM,MottersheadJ,etal.IdentificationofBoltedJointsInterfaceModels[C]//ProceedingsofISMA2002:NoiseandVibrationEngineering.Leuven,Belgium, 2002: 1741-1747.

[8]AhmadianH,JalaliH,MottersheadJ,etal.DynamicModelingofSpotWeldsUsingThinLayerInterfaceTheory[C]//ProceedingsoftheTenthInt.CongressonSoundandVibrationICSV10.Stockholm,Sweden, 2003: 3439-3446.

[9]AhmadianH,MottersheadJ,JamesS,etal.ModellingandUpdatingofLargeSurface-to-surfaceJointsintheAWE-MACEStructure[J].MechanicalSystemsandSignalProcessing, 2006, 20: 868-880.

[10]DesaiC,ZamanM,LightnerJ,etal.Thin-layerElementforInterfacesandJoints[J].InternationalJournalforNumericalandAnalyticalMethodsinGeomechanics, 1984, 8: 19-43.

[11]SharmaK,DesaiC.AnalysisandImplementationofThin-layerElementforInterfacesandJoints[J].JournalofEngineeringMechanics， 1992, 118: 2442-2462.

[12]PandeG,SharmaK.OnJoint/interfaceElementsandAssociatedProblemsofIll-conditioning[J].InternationalJournalforNumericalandAnalyticalMethodsinGeomechanics, 1979, 3: 293-300.

[13]BogradS,ReussP,ASchmidt,etal.ModelingtheDynamicsofMechanicalJoints[J].MechanicalSystemsandSignalProcessing, 2011, 25: 2801-2826.

[14]刘新东, 刘伟. 复合材料力学基础[M]. 西安: 西北工业大学出版社, 2010.

[15]FuWP,HuangYM,ZhangXL,etal.ExperimentalInvestigationofDynamicNormalCharacteristicsofMachinedJointSurfaces[J].JournalofVibrationandAcoustics,TransactionsoftheASME, 2000, 122: 393-398.

[16]石坤, 宋俐, 师俊平, 等. 一种新的机械结构结合部特性分析方法[J]. 机械工程学报, 2013, 49(1): 142-147.

ShiKun,SongLi,ShiJunping,etal.ANewMethodforCharacteristicAnalysisoftheMechanicalStructureJoint[J].JournalofMechanicalEngineering, 2013, 49(1): 142-147.

[17]秦太验, 徐春晖, 周喆. 有限元法及其应用[M]. 北京: 中国农业大学出版社, 2011.

[18]NiJun,ZhuZhenqi.ExperimentalStudyofTangentialMicroDeflectionofInterfaceofMachinedSurfaces[J].JournalofManufacturingScienceandEngineering, 2001, 123: 365-367.

(编辑张洋)

A Constitutive Law Based on Transverse Isotropic Hypothesis and Finite Element Model of Fixed Joints

Zhao JinjuanWang ShijunYang ChaoWang ShiyiYang Huixin

Xi’an University of Technology，Xi’an，710048

A finite element method modeling fixed joints was presented. In the method, the contact layers of the fixed joints were regarded as a homogenous virtual transverse isotropic material. According to the relations among deformations and loads of joints, the nonlinear relations among 5 independent variables and normal stress in constitutive matrix were deduced, and then the relations were introduced into finite element analysis to model fixed joints. The analytical results and experimental results of the joints were compared and the validity of the method was confirmed.

fixed joint； virtual material； finite element； constitutive law

赵金娟，女，1974年生。西安理工大学印刷包装工程学院讲师。主要研究方向为机械接触特性及建模方法。发表论文15篇。王世军(通信作者)，男，1967年生。西安理工大学机械与精密仪器学院副教授。杨超，男，1988年生。西安理工大学机械与精密仪器学院硕士研究生。王诗义，男，1989年生。西安理工大学机械与精密仪器学院硕士研究生。杨慧新，男，1992年生。西安理工大学机械与精密仪器学院硕士研究生。

2015-05-29

国家重点基础研究计划(973计划)资助项目(2009CB724406)；陕西省科技厅科技统筹创新工程重点实验室资助项目(2014SZS10-P05)

TH123

10.3969/j.issn.1004-132X.2016.08.003