MB8变形镁合金超声疲劳试样解析设计

邓海鹏，　何柏林

(华东交通大学 机电工程学院， 南昌 330013)



MB8变形镁合金超声疲劳试样解析设计

邓海鹏，何柏林

(华东交通大学 机电工程学院， 南昌 330013)

对MB8变形镁合金超声疲劳试样进行设计计算。为了减小试样振幅，使试样产生较少的热量，减轻冷却系统压力的同时防止试样产生相变等组织变化，将试样设计成变截面形状。根据试样振动位移方程、边界条件和位移连续条件推导出试样谐振长度与其他尺寸的关系，计算出一系列超声疲劳试样的尺寸。结果表明：变截面圆柱和板状试样随着圆弧过渡段长度增大，谐振长度减小，圆弧过渡半径增大；对于无中间等截面段试样，位移应力系数Cs和应力放大系数M随着圆弧过渡段长度减小而减小；对于含有中间等截面段试样，位移应力系数Cs和应力放大系数M随着中间等截面段长度减小而减小。

变形镁合金；超声疲劳；试样；解析计算

镁合金作为一种轻质结构材料，广泛应用于交通领域等工程结构中。在实际服役过程中，很多零部件因承受低幅、高频循环载荷的作用，会发生超高周疲劳断裂失效[1-3〗[4-5]。

超高周疲劳实验原理与常规疲劳实验不同，所采用的试样形状尺寸必须经过严格设计，使试样具有特定的固有频率和振动特性。只有严格设计的试样安装在疲劳试验机上才能与变幅杆发生谐振，达到高频加载的效果[6-8]；因此，超声疲劳试样的正确设计是进行超声疲劳试验的重要前提。本工作对MB8镁合金圆柱和板状超声疲劳试样进行解析设计，为MB8变形镁合金及其他镁合金超高周疲劳性能实验研究提供参考。

1　超声疲劳实验系统及实验原理

图1所示为典型的超声疲劳纵向拉压实验系统，该系统主要由七个部分组成，分别为计算机控制系统、超声发生器、换能器、变幅杆、光纤位移传感器和放大器。在实验过程中，由于高频振动超声疲劳试样会产生大量热量，所以超声疲劳拉压实验系统还要配备冷却辅助系统对试样进行冷却，冷却介质可以采用压缩冷凝空气或水。

超声疲劳实验过程及原理如下：计算机控制系统通过电信号控制超声发生器；超声发生器根据计算机控制系统的电信号将低频正弦交流电转换成高频交流电；换能器通过磁致伸缩作用将高频交流电转换成高频机械振动；高频机械振动通过固有频率为20 kHz左右的变幅杆将振动位移放大到所需水平；具有20 kHz一阶固有频率的超声疲劳试样与变幅杆连接并发生共振；光纤位移传感器和放大器检测试样端部振动位移、振动频率和振动周次。实验过程中，计算机控制系统调节高频电流大小，利用振动位移与电流的正比例关系从而调节试样振动位移和应力。

2　MB8镁合金超声疲劳试样解析设计

固有频率除了和材料密度和弹性模量等性能有关外，还与材料的形状尺寸有关。为了使试样获得20 kHz的一阶固有频率，同时使试样中间段应力放大，必须对超声疲劳试样进行设计。下面以MB8变形镁合金材料为例，对圆柱状和板状超声疲劳试样进行解析计算。为了在相同应力下使用小的振幅，减轻试样发热，将圆柱状和板状超声疲劳试样设计成变截面。

图1　超声疲劳纵向拉压实验系统[9]Fig.1　Test system of ultrasonic fatigue longitudinal tension and compression[9]

2.1变截面圆柱状超声疲劳试样

2.1.1无中间等截面段圆柱试样

图2　无中间等截面段圆柱试样Fig.2　　　　Cylindrical specimen without uniform cross section in the middle

图2变截面圆柱试样的一维纵向振动方程：

(1)

式中：t为时间；ρ为试样材料的密度；S(x)为试样在x坐标下的截面积；u(x,t)为试样在x坐标下的振动位移；F(x,t)为试样在x位置坐标下截面所受的力。式(1)中：

(2)

u(x,t)=U(x)*eiwt

(3)

式(2)中Ed为试样的动态弹性模量；式(3)中U(x)为坐标为x位置的振动位移幅值；将式(2)，(3)带入式(1)：

U″(x)+p(x)U′(x)+k2U(x)=0

(4)

式(4)中：

(5)

式(5)中，f为试样谐振频率。假设：

(6)

(7)

(8)

(9)

(10)

(11)

将式(6)，(7)，(8)，(9)，(10)带入式(4)中可以解得：

(12)

(13)

式(12)和(13)中，C1,C2,C3和C4是位移方程化成通解后得到的常数，根据边界条件和连续性条件：

(14)

(15)

式(14)中，A0表示试样在端部振动幅值，可以解得谐振长度L2为：

(16)

过渡段曲线方程为：

(17)

将曲线上的点(L1，R2)带入方程(17)中，可以解得：

(18)

根据式(13)位移通解U(x)可以求得变截面段应变通解：

(19)

上式中：

(20)

由式(19)，可以求得：

εmax=βA0φ(L1,L2)

(21)

σmax=Edεmax=EdβA0φ(L1,L2)

(22)

所以，位移应力系数Cs和应力放大系数M为：

(23)

(24)

MB8变形镁合金物理性能及求解L2和R0相关参数如下：

Ed=45GPa,ρ=1870kg/m3,f=20kHz

(25)

将式(25)中的参数带入式(16)和式(18)中，可以得到无中间等截面段的变截面圆柱状试样尺寸结果(见表1)。

表1　无中间等截面段圆柱试样计算结果

由表1可知：对于相同R1和R2的无中间等截面段圆柱试样，谐振长度、位移应力系数和应力放大系数随着圆弧过渡段长度的增大而减小，圆弧过渡半径随着圆弧过渡段长度的增大而增大。

2.1.2有中间等截面段圆柱试样

有中间等截面段圆柱试样如图3所示。

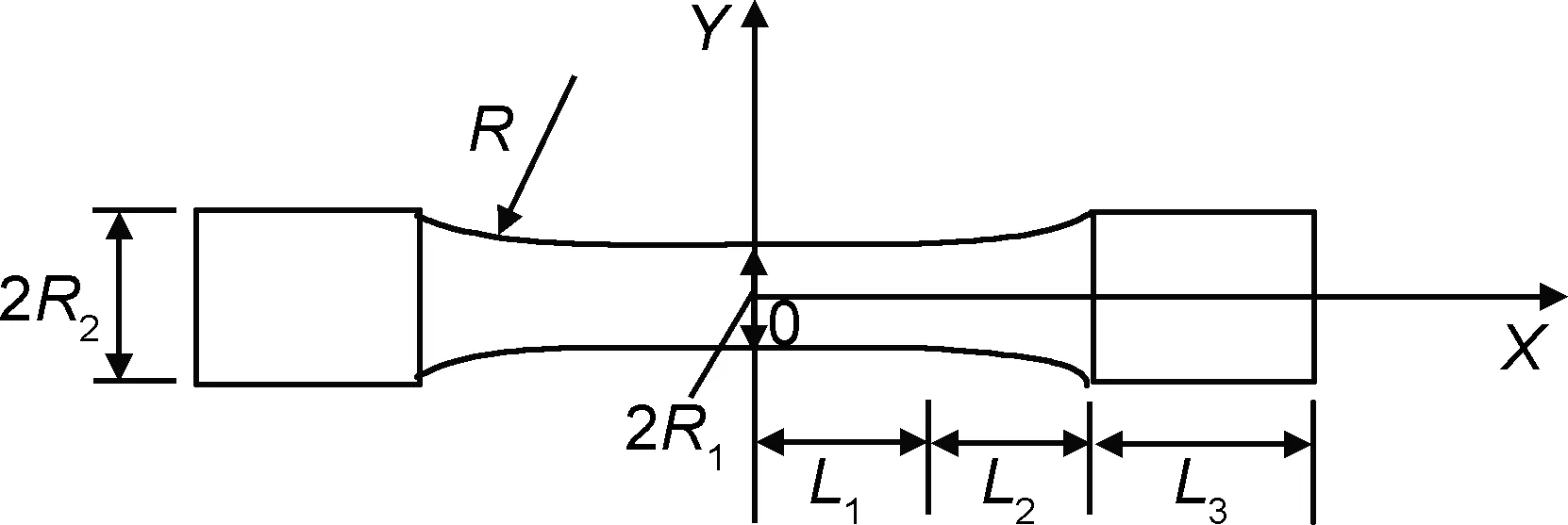
图3　有中间等截面段圆柱状试样Fig.3　　　　Cylindrical specimen with uniform cross section in the middle

图3试样的U(x)通解为:

(26)

U(x)=A0φ

(27)

(28)

式(26)，(27)，(28)中：

(29)

将边界条件和连续性条件带入式(27)中，解得谐振长度L3为：

(30)

R0计算结果为：

(31)

根据式(26)中U(x)通解，求得最大应力σmax：

(32)

所以，位移应力系数CS和应力放大系数M为：

(33)

(34)

将式(25)中的参数带入式(30)和(31)中，可以得到有中间等截面段的变截面圆柱状试样尺寸计算结果(见表2)。

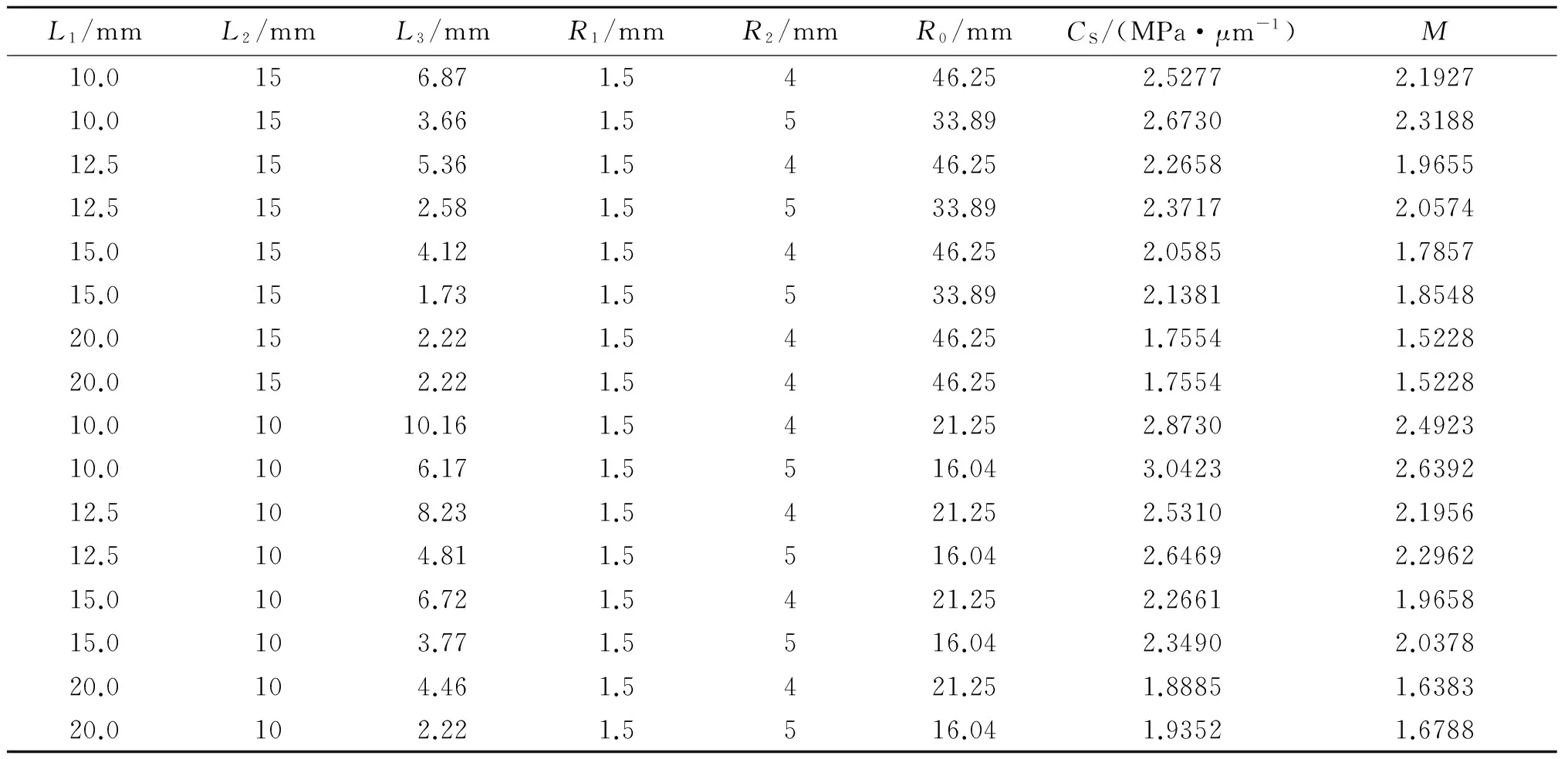
表2　有中间等截面段圆柱状试样计算结果

由表2可知：对于相同L1，R1和R2的有中间等截面段圆柱试样，谐振长度随着圆弧过渡段长度的增大而减小，圆弧过渡半径随着圆弧过渡段长度的增大而增大；对于相同L2，R1和R2的有中间等截面段圆柱试样，位移应力系数和应力放大系数随着中间等截面段长度的减小而减小。

2.2变截面板状超声疲劳板状试样

2.2.1无中间等截面段板状试样

对于图4无中间段等截面段板状试样有：

(35)

(36)

(37)

(38)

(39)

图4　无中间等截面段板状试样Fig.4　Plate specimen without uniform cross section in the middle

该类型试样纵向振动位移方程：

U″(x)+2αU′(x)+k2U(x)=0

(40)

将已知条件式(35)，(36)，(37)，(38)和(39)带入式(40)中，求得通解：

U(x)=A0φ(L1,L2)sinh(βx)exp(αx)

(41)

(42)

式(40)中：

(43)

将边界条件和位移连续条件带入式(41)和(42)，可以解得谐振长度L2为：

(44)

变截面段曲线方程：

(45)

将曲线上的点(L1，b2/2)带入曲线方程(45)，可以解得：

(46)

根据式(41)和(42)中U(x)的通解，求得最大应力σmax：

(47)

所以，位移应力系数Cs和应力放大系数M为：

(48)

(49)

将式(25)中的参数带入式(44)和(46)中，可以得到无中间等截面段的变截面板状试样尺寸计算结果(见表3)。

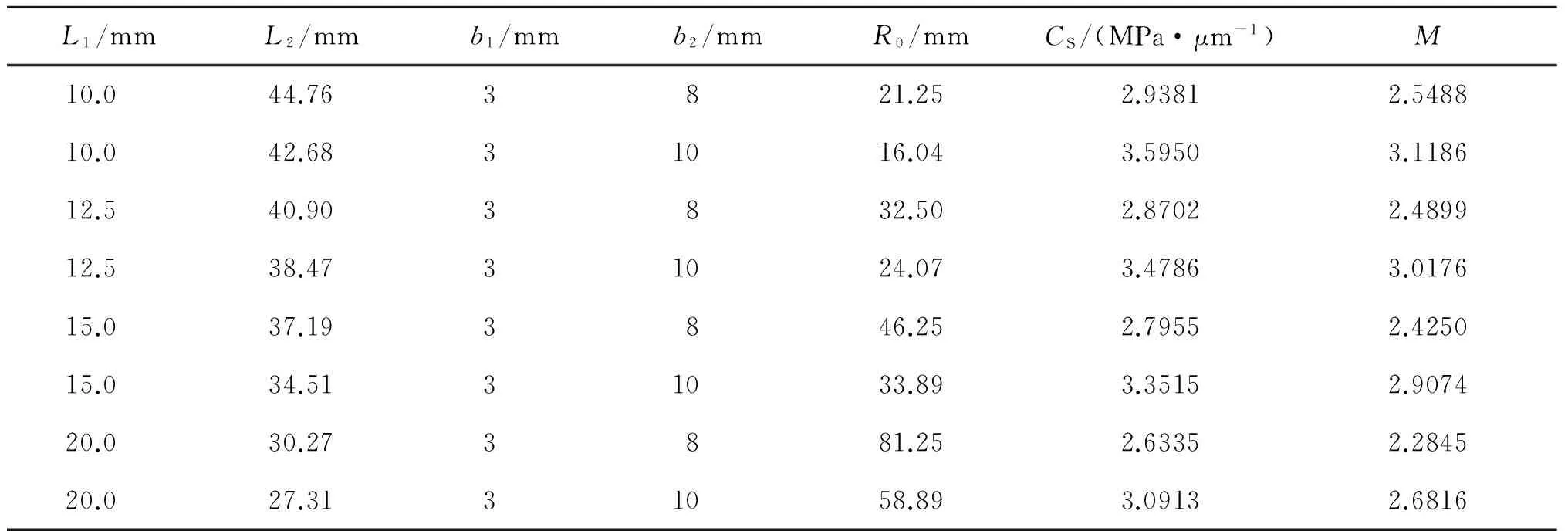
表3　无中间等截面段板状试样计算结果

由表3可知：对于相同b1和b2的无中间等截面段板状试样，谐振长度、位移应力系数和应力放大系数随着圆弧过渡段长度的增大而减小，圆弧过渡半径随着圆弧过渡段长度的增大而增大。

2.2.2有中间等截面段板状试样

有中间等截面段板状试样如图5所示。

图5试样U(x)通解为:

(50)

U(x)=C5exp[(β-α)(x-L1)]+C6

(51)

(52)

上述三式中：

C2=A0βφ

(53)

(54)

(55)

将边界条件和连续位移条件带入到式(50)，(51)，(52)中，解得谐振长度L3为：

(56)

R0计算结果为：

(57)

根据式(50)，(51)和(52)中U(x)通解，求得最大应力σmax：

=Edβkφ(L1,L2,L3)A0

(58)

上式中：

(59)

所以，位移应力系数Cs和应力放大系数M为：

(60)

(61)

将式(25)中的参数带入式(56)和(57)中，可以得到有中间等截面段的变截面板状试样尺寸计算结果(见表4)。

由表4可知：对于相同L1，b1和b2的有中间等截面段圆柱试样，谐振长度随着圆弧过渡段长度的增大而减小，圆弧过渡半径随着圆弧过渡段长度的增大而增大；对于相同L2，b1和b2的有中间等截面段圆柱试样，位移应力系数和应力放大系数随着中间等截面段长度的减小而减小。

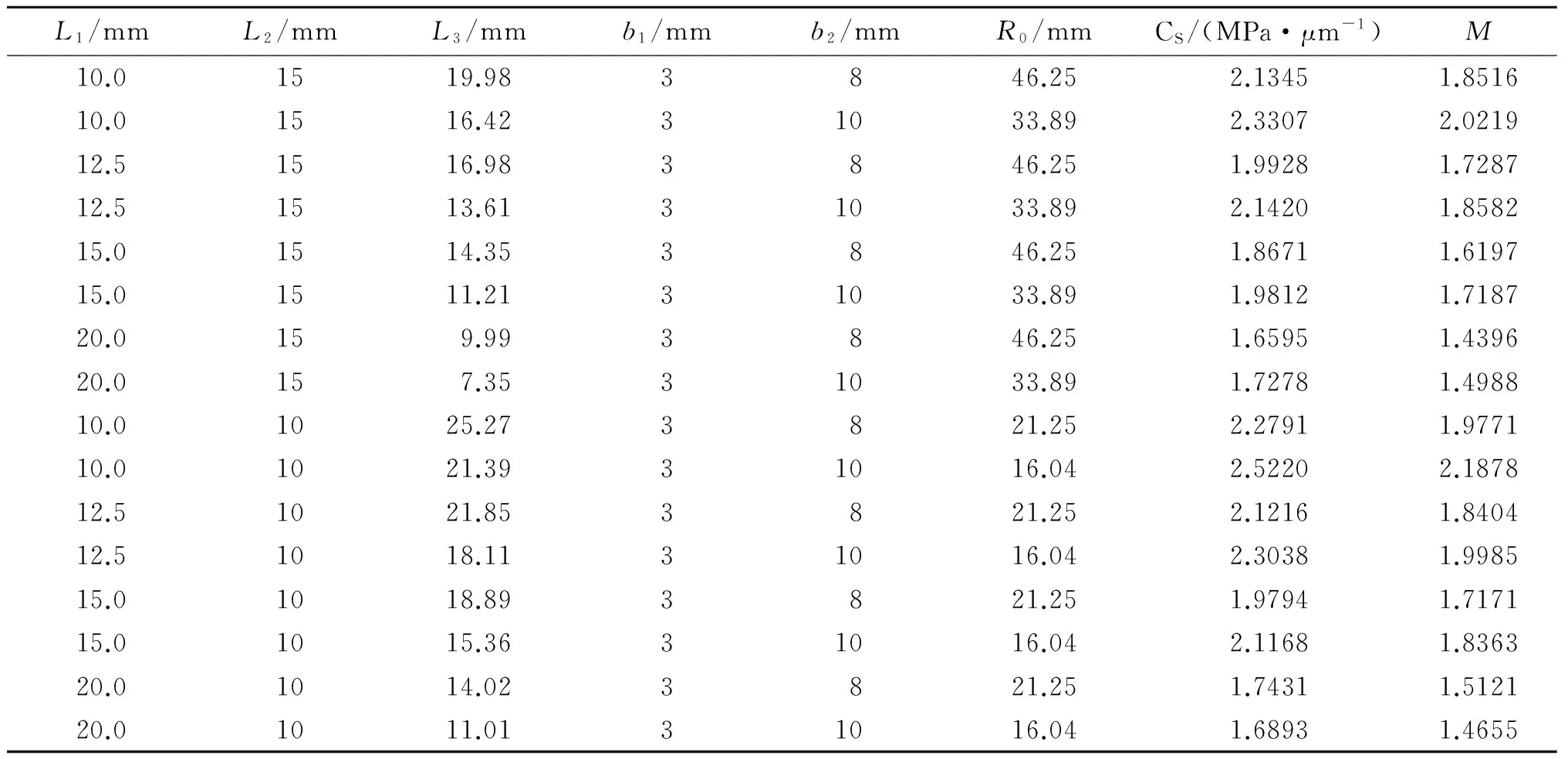
表4　有中间等截面段板状试样计算结果

3　结论

(1)镁合金熔点和相变温度低，高频加载产生的内耗会使试样温度急剧升高，引起组织变化。MB8镁合金超声疲劳试样为了减小试样振幅，使试样产生较少的热量，减轻冷却系统压力的同时防止试样产生相变等组织变化，将试样设计成变截面形状。变截面试样可以在较小的振幅下获得较大的应力。

(2)变截面圆柱和板状试样随着圆弧过渡段长度增大，谐振长度减小，圆弧过渡半径增大。对于无中间等截面段试样，位移应力系数和应力放大系数随着圆弧过渡段长度减小而减小。对于含有中间等截面段试样，位移应力系数和应力放大系数随着中间等截面段长度减小而减小。

[1] 李姗，王伯健．变形镁合金的研究与开发应用[J]．热加工工艺，2007，36(6)：65-68．

(LI S，WANG B J．Research and application development of wrought magnesium alloy[J]．Metal Hot Working Technology，2007，36(6)：65-68．)

[2] MOHD S，OTSUKA Y，MIYASHITA Y，etal．Statistic characteristics of fatigue properties in magnesium alloy[J]．Procedia Engineering，2011，10(7):1232-1237．

[3] OGAREVIC V V，STEPHENS R I．Fatigue of magnesium alloys[J]．Annu Rev Mater Sci，1990，20：141-177．

[4] 李夷，李慧中，姜俊，等．热处理对AZ80镁合金疲劳性能的影响[J]．航空材料学报，2014，34(6)：33-39．

(LI Y，LI H Z，JIANG J，etal．Effect of heat treatment on fatigue properties of AZ80 magnesium alloy[J]．Journal of Aeronautical Materials，2014，34(6)：33-39．)

[5] 杨少锋，王再友．压铸镁合金的研究进展及发展趋势[J]．材料工程，2013(11)：81-88．

(YANG S F，WANG Z Y．New research development and its prospect on die-cast magnesium alloys[J]．Journal of Materials Engineering，2013(11)：81-88．)

[6] POTZIES C，KAINER K U．Fatigue of magnesium alloys[J]．Advanced Engineering Materials，2004，6(5)：281-289．

[7] 闫思江，李凡国．超声疲劳试验方法及其应用[J]．力学与实践，2004，26：25-29．

(YAN S J，LI F G．Ultrasonic fatigue testing and its applications[J]．Mechanics in Engineering，2004，26：25-29．

[8] 薛红前，陶华，BATHIASC．超声疲劳试样设计[J]．航空学报，2004，25(4)：425-428．

(XUE H Q，TAO H，BATHIAS C．The design of specimen for fatigue test at ultrasonic frequency[J]．Acta Aeronautica et Aeronautica Sinica，2004，25(4)：425-428．)

[9] 权高峰．5A06铝合金焊接接头超高周疲劳性能研究[D]．天津：天津大学，2012．

Design of Ultrasonic Fatigue Specimen of MB8 Wrought Magnesium Alloy by Analytic Method

DENG Haipeng，HE Bolin

(College of Mechanical and Electrical Engineering, East China Jiaotong University, Nanchang 330013, China)

Ultrasonic fatigue specimen of MB8 wrought magnesium alloy was designed by calculation. In order to reduce the vibration amplitude, heat and pressure of the cooling system and also to protect the phase change, the sample was designed into variable cross-section. Based on the vibration displacement equation, boundary condition and displacement continuity condition, the relationship between the resonant length and other dimensions of the sample was derived. A series of size of ultrasonic fatigue specimens was calculated, which provided reference for the research of ultrasonic fatigue test of magnesium alloy. The results show that the resonance length decreases with the increase of the length of transition section, and the arc transition radius increases with the increase of the length of arc transition section.With the decrease of the length of arc transition section, Cs and M decreases for the specimen without uniform cross section in middle. With the decrease of the length of uniform cross section in the middle, Cs and M decreased for the specimen with uniform cross section in the middle.

wrought magnesium alloy；ultrasonic fatigue；specimen；analytic calculation

(责任编辑：徐永祥)

2015-12-30；

2016-03-12

国家自然科学基金(51365014)；江西省自然科学基金(20151BAB206007)

邓海鹏(1992—)，男，硕士，主要从事金属材料疲劳性能研究，(E-mail)1227871078@qq.com。

10.11868/j.issn.1005-5053.2016.4.009

V216.3

A

1005-5053(2016)04-0064-07