对流作用下Al-4.7%Cu合金枝晶生长的形貌特征和成分分布的数值模拟

周靖超,　李　日,　杨莹莹,　赵朝阳

(河北工业大学 材料学院，天津 300130)



对流作用下Al-4.7%Cu合金枝晶生长的形貌特征和成分分布的数值模拟

周靖超,李日,杨莹莹,赵朝阳

(河北工业大学 材料学院，天津 300130)

建立了用于模拟Al-4.7%Cu(质量分数)单相固溶体合金凝固过程温度场、流场、溶质场以及微观组织模拟的元胞自动机-格子玻尔兹曼方法(CA-LBM)数值模型,分析对流作用下枝晶生长的形貌与成分变化。模型处理溶质场计算中固液(S/L)界面处溶质的分配过程，使浓度场的变化和实际的传输过程更加相符。计算结果表明，与不计入流动过程的纯扩散型合金凝固过程相比较，对流对合金枝晶形貌的影响显著，呈现非对称生长形貌。在强制对流条件下，枝晶晶粒大小呈均匀化趋势，枝晶间的局部区域的成分更加均匀，在整体凝固区域内的成分呈现出上游到下游的一定的梯度化趋势。

合金凝固；微观组织模拟；CA-LBM；成分分布；枝晶形貌

在固溶体合金枝晶生长过程中，如果存在强制对流和自然对流，则会影响枝晶内成分以及枝晶周围熔体成分的分布状态，最终形成A型偏析、正偏析、V型偏析等宏观偏析[1-2]。宏观偏析对铸件性能有显著影响，因此，研究强制对流对组织形貌及成分分布的影响规律具有重要意义。

格子玻尔兹曼方法(Lattice Boltzmann Method，LBM)是近20年来发展起来的一种新的数值计算方法[3-4]。与传统的连续性数值方法相比，LBM算法有显著优势，如算法简洁、计算效率高、易于处理复杂条件、稳定性好等。在多相多组分流、多孔介质流、颗粒悬浮等领域[5-7]取得了显著成果。目前，LBM在凝固领域也开始得到应用[8-13]。这些研究主要集中在凝固过程晶体形貌方面，对结合晶体形貌进行成分分布的研究较少，但是成分偏析(宏观偏析和微观偏析)对材料性能是非常重要的。

本工作采用CA(Cellular Automaton, CA)计算合金凝固过程中的微观组织，采用LBM计算凝固过程中的流场、温度场以及溶质场，构建一个新的溶质连续分配的CA-LBM模型，模型在溶质传输方面做了很大的改进，更能体现实际的溶质分配传输过程。采用新模型分析对流条件下枝晶的成分分布的定量变化，并进行和成分相关的形貌分析研究。

1　模型的描述和数值计算方法

在小Peclet数和低Reynols数的条件下，建立元胞自动机法(CA)和格子波尔曼方法(LBM)的耦合模型，用来模拟单相固溶体合金在强制对流条件下的枝晶生长。用CA方法计算凝固过程中的枝晶生长，用LBM方法计算凝固过程中的流场、温度场及溶质场。

1.1LBM模型

采用基于单松弛时间的LBGK(Bhatnagar-Gross-Krook)方法的D2Q9模型[12]。在强制对流条件下，浮力项相对很小，可以忽略不计。在考虑潜热和浓度源项的情况下，计算流场、温度场和浓度场的粒子分布函数的时空演化方程为式为[9,11]。

fi(r+eiΔt,t+Δt)=fi(r,t)+

(1)

hi(r+eiΔt,t+Δt)=hi(r,t)+

(2)

gi(r+eiΔt,t+Δt)=gi(r,t)+

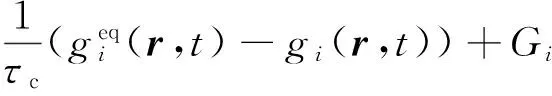
(3)

在D2Q9格式中，在格点上的离散粒子速度ei(i=0～8)可表示为式(4)：

(4)

式中：c=Δx/Δt为格子速度;Δx为空间步长。

流体的宏观物理量，如流体密度ρ，速度u，浓度Cl及温度T等可以由相应的粒子分布函数求得(式(5))。

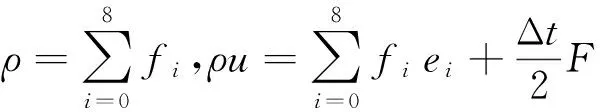
(5)

式中，F为液相的浮力。根据Boussinesq近似，浮力项中的密度为温度梯度和浓度梯度的线性函数。因此，浮力项近似为式(6)[14]：

F=gρ0[βT(T-T0)+βC(C-C0)]

(6)

式中：ρ0为温度为T0、浓度为C0时的密度；g为重力加速度；βT和βC分别为温度和浓度膨胀系数。在本研究中，对于强制对流的模拟，取F=0。在式(1)中的外力项Fi由液相浮力F离散化表示为式(7)[9]：

(7)

式中：wi为权重系数，其取值为式(8)。

(8)

当考虑流动影响时，(1)～(3)式中的平衡分布函数分别为式(9)，(10)，(11)[15]：

(9)

(10)

(11)

根据Chapman-Enskog分析，连续性方程、N-S方程和对流扩散方程可以由上述LB方程得到。其中，流体动力学黏度ν、热扩散系数α及溶质扩散系数D分别与流动松弛时间τf、温度松弛时间τt和浓度松弛时间τc有关(式(12))[9]。

(12)

式(2)，(3)中源项Hi和Gi由计算枝晶生长的CA模型给出。

1.2CA模型

(13)

(14)

(15)

(16)

式中，k是溶质分配系数。

假定在S/L界面服从局部平衡条件Cs=kCl，在一个时间步长Δt内，在S/L界面网格中，随着该网格固相分数的增加，释放的溶质ΔCl和潜热ΔT分别表示为式(17)、式(18)[20]：

ΔCl=ΔφsCl(1-k)

(17)

ΔT=ΔφsΔH/Cp

(18)

式中：ΔH为凝固潜热；Cp为热容。

由上，式(2)，(3)中的源项为式(19)，(20)。

Hi=ωiΔφsΔH/Cp，

(19)

Gi=ωiΔφsCl(1-k)

(20)

元胞分为三种状态：固态、液态、界面(S/L)元胞。对每个元胞都赋予温度、浓度、生长角和固相率等属性。当界面元胞的固相率达到1时，元胞属性值变为固态，并且该元胞排出的溶质ΔCl=ΔφsCl(1-k)分配到与其相邻的元胞中。成为固态的元胞将捕获周围的液态元胞使其成为界面元胞，本研究采用的捕获方式为Moore的8邻居法则[20]。

1.3边界条件

团队管理的基本要素，是促进团队提高其业绩的重要保证，也是团队发展的重要条件，同时对促进企业规范化管理和发展具有重要作用。基于此，本文在学习型组织理论的基础上，提出团队管理的优化措施，进一步丰富团队管理方式的相关理论，对企业经济效益的实现具有重要参考价值。

在一个二维{(x,y)|0≤x≤L,0≤y≤L}的计算区域中，四个区域边界和固液边界上的未知分布函数会严重影响流场、温度场及浓度场的计算。因此，对于边界条件做如下处理：

(1)在自然对流的条件下，对于四个区域边界和固液边界，计算流场时，采用无滑移的反弹边界格式处理[11]；计算温度场时，假定固液的热传导相同，四个边界的温度为一固定值T0，用非平衡外推法计算四个区域边界上的温度分布函数。由于在固液相线温度区间，液相的导热系数和固相的导热系数非常接近，简化为相等处理；计算溶质场时，忽略固相中的溶质扩散，四个区域边界采用无扩散边界条件，固液边界采用反弹格式处理。

(2)在强制对流的条件下，左右区域边界分别为进出流口，分别表示为u(x,y)|x=0=(uin,0)和∂xux|y=L=0，采用非平衡外推格式处理[15]，上下两个区域边界采用能保证质量和动量守恒的周期性边界条件。

2　模拟结果及讨论

2.1合金溶体的物性参数

选取Al-4.7%Cu(质量分数，下同)合金为模拟研究材料(计算热物性参数见表1)。

表1　Al-4.7%Cu的物性参数

2.2自然对流作用下单枝晶形貌及成分分布

自然对流会使溶体中的溶度分布发生变化，首先模拟出纯扩散和存在自然对流的情况下的成分分布及枝晶形貌。模拟中将二维的计算区域剖分为400×400的正方形均匀网格，选取网格的尺寸为0.5 μm。将一个晶核置于点(200,200)处，晶核的固相溶质成分为kC0及择优取向为0°，其余液相成分为初始成分C0。计算区域的初始过冷度均为ΔT=4 K，并且四个壁面边界的温度为Tb=913K不变。

图1中，(a～c)为纯扩散枝晶生长动态成分变化和形貌变化，(d～f)为考虑自然对流作用下的枝晶生长动态成分变化和形貌变化，两种状态的固相率依次为0.01，0.049，0.12。

从图1的对比可以看出自然对流的存在使溶体内部的成分发生变化，在区域上端的浓度偏高，下端的区域浓度偏低。这是由于当枝晶生长时排出的溶质和潜热使凝固区域产生浓度和温度梯度，在重力的作用下产生了自然流动，流动方向如图1(f)所示。成分在自然对流作用和溶质尖端梯度的作用下被扩散到上端，形成上端浓度高于下端的现象。由于自然对流的作用下，使溶体内部的成分发生变化，进而使枝晶的生长形貌也发生了变化，对比图1(c)，(f)可以得出，在迎流方向上的枝晶生长的较快，逆流方向上的枝晶生长的较慢。

图1　　　　Al-4.7%Cu合金单枝晶凝固过程中的成分和形貌动态变化：(a,d)φs=0.01；(b,e)φs=0.014;(c,f)φs=0.02(φs为固相分数)；(a～c)在纯扩散的条件下生长过程；(d～f)在由浮力引起的自然对流的作用下生长过程Fig.1　　　　Change of single-dendritic morphology and solutal distribution of Al-4.7 %Cu alloy solidification:(a,d)φs=0.01;(b,e)φs=0.014;(c,f)φs=0.02(φs:solid fraction of solidification);(a-c)dendritic growth 　　　without convection;(d-f)dendritic growth under natural convection caused by buoyancy

图2为当固相率为0.12时纯扩散和自然对流条件下，在y=100，y=200，y=300上的浓度分布变化曲线。从图2(a)，(b)，(c)中可以看出，在自然对流作用下的枝晶尖端(图2(b)尖端位置)附近的浓度梯度明显的比纯扩散条件下的大，远离尖端部分最终趋于浓度相等状态，这一现象表明在自然对流作用下溶质扩散加剧。在y=100的检测线上(图2(a))，存在自然对流时的成分(约4.65%)比纯扩散下的成分(约4.73%)偏低。在y=200的检测线上(图2(b))，自然对流作用下的枝晶S/L边界的成分比纯扩散的要高，这是在流场的作用下，计算区域下端的成分通过y=200这一水平面向上端扩散，同时导致在y=200的枝晶尖端溶质偏高，致使自然对流作用下枝晶生长较慢(形貌对比如图1(c)，(f))。在y=300的检测线上(图2(c))，在自然对流作用下y=300上的浓度比纯扩散条件下大，抑制了枝晶的生长，致使枝晶生长的较短(形貌对比如图1(c)，(f))。

图2　　　　Al-4.7%Cu合金单枝晶凝固φs=0.12时的浓度曲线分析　(a)在y=100纯扩散和自然对流条件下的浓度对比；(b)在y=200纯扩散和自然对流条件下的浓度对比；(c)在y=300纯扩散和自然对流条件下的浓度对比Fig.2　Single-dendritic solutal distribution of Al-4.7%Cu alloy when φs=0.12　(a)comparison of solute between natural convection and without convection at y=100;arison of solute between natural convection and without convection at y=300

为了定量的研究对流对枝晶生长的影响，分别对纯扩散、自然对流、强制对流条件下枝晶尖端的生长速率随时间变化的模拟结果进行了分析，结果如图3、图4所示。图3为自然对流和纯扩散条件下枝晶尖端的生长速率随时间变化图，图4为强制对流和纯扩散条件下枝晶尖端的生长速率随时间变化图。

从图3和图4中可以看出，在凝固初始阶段的极短时间内，枝晶尖端的生长速率都很快，随着凝固的进行，溶质不断的排出和潜热释放,使枝晶尖端的溶质和热量富集，导致枝晶尖端的生长速率急剧的降低。但经过一段时间后，由于溶质和潜热在扩散及对流的条件下使枝晶尖端的状态达到稳定状态，进而枝晶尖端的生长速率趋于稳定，表现为生长速率大小不变。从图3、图4中可以得出，在对流的条件下，迎流尖端的枝晶生长速率最高，逆流尖端的生长速率最低，其他尖端的生长速率基本上和纯扩散的条件下相同。比较图3和图4中强制对流和自然对流的枝晶尖端生长速率，在强制对流条件下迎流尖端的生长速率比自然对流条件下大，而强制对流条件下逆流尖端的生长速率比自然对流条件下小，这表明强制对流对溶质及潜热的影响较大，使枝晶生长速率发生很大变化，所以，在工业生产上强制对流对凝固过程及凝固组织有很大影响。

图3　对应图1中枝晶尖端的生长速率随时间的变化Fig.3　Tip velocites vary with time for the case of Fig.1

图4　对应图5中枝晶尖端的生长速率随时间的变化Fig.4　Tip velocities vary with time for the case of Fig.5

2.3强制对流作用下单枝晶及多枝晶的枝晶形貌及成分分布

强制对流模拟选择在二维型腔中进行，熔体仍选取Al-4.7%Cu合金。由于溶质扩散比温度扩散小四个数量级左右[22]，所以枝晶生长主要受溶质浓度差驱动。假设溶体温度均匀，初始过冷度ΔT=4K，并以100 k/s速率冷却。流体从左边界以恒定速度uin=0.003m/s流入型腔，从右边界流出。

计算结果如图5、图6所示。图5为单个枝晶在强制对流情况下的情况，图6为多个枝晶的无强制对流和有强制对流情况下的比较，其中图6(a)，(b)，(c)为纯溶质扩散无强制对流的计算结果，图6(d)，(e)，(f)为存在强制对流时的计算结果。

图5为单个枝晶在强制对流的作用下的成分分布及枝晶生长形貌。计算区域选取400×400正方形均匀网格，选取网格的尺寸为0.5 μm。从图5(a)中可以看出，强制对流的条件下，枝晶的形态呈非对称生长，上游的迎流枝晶臂生长的较快，而下游的逆流方向上的枝晶生长的较慢。分析图5(b)，在强制对流的作用下，上游枝晶尖端的成分浓度(5.52%)比下游尖端的成分浓度(5.72%)低，促进了上游枝晶尖端的生长，溶质在下游尖端富集，抑制了下游枝晶尖端的生长，所以出现了枝晶上下游生长的不对称性。

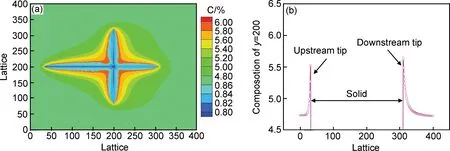
图5　强制对流下Al-4.7%Cu合金单枝晶凝固过程成分分布及枝晶形貌(a)和y=200上的对应浓度大小(b)Fig.5　　　　Dendritic morphology and solutal distribution of Al-4.7%Cu alloy solidification under forced convection (a) and solute change at y=200 (b)

图6为多枝晶在强制对流的作用下的成分分布及枝晶生长形貌。计算区域选取为480×480正方形均匀网格，选取网格的尺寸为1 μm。其他参数的选取与单个枝晶的参数设置相同，并取六个晶粒随机形核。

图6(a)～(c)为纯扩散条件下枝晶一次轴沿最优生长方向生长。随温度的降低，出现了明显的二次枝晶，当温度足够低时，枝晶呈现出粗化的趋势。图6(a)中有明显的溶质包络环，当枝晶间距逐渐减小，包络环互相融合，浓度分布趋于平缓。图6(d～f)为强制对流条件下的枝晶生长。与纯扩散时的固相率相同情况下的结果相比较，在对流的作用下枝晶的迎流端生长较快，呈明显的不对称生长状态。由图可知，图6(e)，(f)中，左边界处区域的溶质浓度较高，从左到右溶质浓度有明显减小的趋势，这是因为，在强制对流的作用下，枝晶排出的溶质扩散较快，导致枝晶快速生长，枝晶快速闭合，形成屏障，使得上游的溶质不能向下游扩散，以至集聚在边界附近。由图6(e)还可以发现一个有趣的现象，就是中央的一个枝晶生长得要比无强制对流时要快得多(图6(b)，(e)中红色虚线环圈出的晶粒)，这也是因为强制对流使得溶质可以迅速扩散，促进了中央枝晶的快速生长，这为工业上可以采用强制对流来进行合金晶粒的均匀化提供了理论依据。

为了定量对比分析强制对流对总体区域的成分影响，在计算区域的垂直方向上选取三条水平线y=120，y=240，y=360，对线上的溶质浓度分布进行纯扩散情况下和强制对流情况下的比较分析，如图7(固相率为0.456时)所示。

在三条水平线上，存在强制对流的条件下，在整个凝固区间存在着一个沿流动方向的溶质浓度梯度(图7(a～c)的红色曲线)，即整体凝固区域内的梯度。而在纯扩散的条件下，全局浓度从左端到右端的变化较为平缓，不存在明显的浓度梯度(图7(a～c)中的黑色曲线)。

对这两种情况下的浓度分布进行局域分析，可知，当存在强制对流时，除个别部位外，大部分区域浓度梯度变化较为缓和，即在局部范围内，成分混合较为均匀。在纯扩散的条件下，在局部范围内，熔体中的浓度变化梯度较有强制对流的情况要陡一些，即局部成分梯度较大。

图7　　　　Al-4.7%Cu合金多枝晶凝固φs=0.45时的浓度曲线分析　(a)在y=120纯扩散和强制对流条件下的浓度对比；(b)在y=240纯扩散和强制对流条件下的浓度对比；(c)在y=360纯扩散和强制对流条件下的浓度对比；下方为对应的成分线上的枝晶生长形貌图Fig.7　　　　Multi-dendritic solutal distribution of Al-4.7%Cu alloy　(a)comparison of solute between forced convection and without convection at y=120;(b)comparison of solute between forced convection and without convection at y=240;(c)comparison of solute between forced convection and without convection at y=360

3　结　论

(1)建立了计算单相固溶体凝固过程温度场、流场、溶质场的CA-LBM耦合模型。用LBM计算凝固过程中的宏观场，用CA方法计算凝固过程的微观组织。模型改善了S/L边界的溶质传输过程，使溶质的变化更符合实际的传输过程；

(2)利用所建立的CA-LBM模型，模拟了Al-4.7%Cu合金的单枝晶及多枝晶在强制对流和自然对流条件下的凝固过程。计算结果表明：对流对枝晶形态有很大影响，对流使枝晶尖端的浓度发生变化，造成枝晶的非对称性生长；对流使枝晶间及整个凝固区间的浓度产生明显的变化，使小范围的枝晶区间溶体的浓度均匀化，但在整个凝固区间存在着一个沿流动方向的溶质浓度梯度；强制对流和自然对流对凝固枝晶形貌有很大的影响，最终会导致铸件不同部位性能分布的差异。

[1] 周冰，康永林，祁明凡，等．AZ91D镁合金强制对流流变压铸组织与性能[J]．材料工程，2014(10)：1-5．

(ZHOU B，KANG Y L，QI M F，etal．Microstructure and tensile properties of AZ91D magnesium alloy by forced convection rheo-diecasting process [J]．Journal of Materials Engineering，2014(10)：1-5．)

[2] 余欢，李炼，周珍珍，等．不同冷速作用下K424镍基高温合金相变及组织形成规律[J]．航空材料学报，2014，34(3)：1-7．

(YU H，LI L，ZHOU Z Z，etal．Phase transformation and micostructure formation of K424 superalloy with different cooling rate[J]．Journal of Aeronautical Materials，2014，34(3)：1-7．)

[3] CHEN S Y，DOOLEN G D，MATTHAEUS W H．Lattice gas automata for simple and complex fluids [J]．Journal of Statistical Physics，1991，64(5/6)：1133-1162．

[4] QIAN Y H，DHUMIERES D，LALLEMAND P．Diffusion simulation with a deterministic one-dimensional lattice-gas model[J]．Journal of Statistical Physics，1992，68(3/4)：563-573．

[5] FENG Z G，MICHAELIDES E E．The immersed boundary-lattice Boltzmann method for solving fluid-particles interaction problems[J].Journal of Computational Physics，2004，195(2)：602-628．

[6] 朱炼华，郭照立．基于格子Boltzmann方法的多孔介质流动模拟GPU加速[J]．计算物理，2015，32(1)：20-26．

(ZHU L H，GUO Z L．GPU accelerated lattice Boltzmann simulation of flow in porous media[J]．Chinese Journal of Computational Physics，2015，32(1)：20-26．)

[7] FU Y，ZHAO S，WANG W，etal．Application of lattice Boltzmann method for simulation of multiphase/multicomponent flow in microfluidics[J]．CIESC Journal，2014，65(7)：2535-2543．

[8] MILLER W，SUCCI S，MANSUTTI D．Lattice Boltzmann model for anisotropic liquid-solid phase transition[J]．Physical Review Letters，2001，86(16)：3578-3581．

[9] YIN H，FELICELLI S D，WANG L．Simulation of a dendritic microstructure with the lattice Boltzmann and cellular automaton methods[J].Acta Materialia，2011，59(8)：3124-3136．

[10] ZHANG X F，LI X K．Simulation of dendritic growth of Al-4wt.%Cu alloy from an undercooled melt[J]．International Journal of Materials Research，2015，106(10)：1053-1059．

[11] SUN D K，ZHU M F，PAN S Y，etal．Lattice Boltzmann modeling of dendritic growth in forced and natural convection[J]．Computers & Mathematics with Applications，2011，61(12)：3585-3592．

[12] ESHRAGHI M，JELINEK B，FELICELLI S D．Large-scale three-dimensional simulation of dendritic solidification using lattice Boltzmann method[J]．JOM，2015，67(8)：1786-1792．

[13] ZHU M F，PAN S Y，SUN D K，etal．Numerical simulation of microstructure evolution during alloy solidification by using cellular automaton method[J]．ISIJ International，2010，50(12)：1851-1858．

[14] 郭照立，李青，郑楚光．双扩散自然对流的格子Boltzmann模拟[J]．计算物理，2002，06：483-487．

(GUO Z L， LI Q， ZHENG C G．Lattice Boltzmann simulation of double diffusive natural convection [J]．Chinese Journal of Computational Physics，2002，19(6)：483-487．)

[15] SUN D K，ZHU M F，DAI T，etal．Modeling of dendritic growth in ternary alloy solidification with melt convection[J]．International Journal of Cast Metals Research，2011，24(3/4)：177-183．

[16] ZHU M F，STEFANESCU D M．Virtual front tracking model for the quantitative modeling of dendritic growth in solidification of alloys[J]．Acta Materialia，2007，55(5)：1741-1755．

[17] 郭洪民，杨湘杰．凝固微观组织的多层次模拟[J]．中国有色金属学报，2004，14(6)：928-933．

(GUO H M，YANG X J．Multi-scale modeling of solidification microstructure[J]．The Chinese Journal of Nonferrous Metals，2004，14(6)：928-933．)

[18] 朱鸣芳，于金，洪俊杓．金属凝固显微组织的计算机模拟[J]．中国工程科学，2004, 6(5)：8-16．

(ZHU M F，YU J，HONG J B．Computer simulation of metal solidification microstructures[J]．Engineering Science，2004，6(5)：8-16．)

[19] 陈瑞，许庆彦，柳百成．基于元胞自动机方法的定向凝固枝晶竞争生长数值模拟[J]．物理学报，2014，63(18)：449-460．

(CHEN R，XU Q Y，LIU B C．Simulation of dendritic competitive growth during directional solidifiction using modified cellular automaton method[J]．Acta Phys Sin，2014，63(18)：449-460．)

[20] JELINEK B，ESHRAGHI M，FELICELLI S，etal．Large-scale parallel lattice Boltzmann-cellular automaton model of two-dimensional dendritic growth[J]．Computer Physics Communications，2014，185(3)：939-947．

[21] 李日，沈焕弟，冯长海，等．一个新的用于元胞自动机模拟微观组织的溶质分配模型及其计算验证[J]．物理学报，2013，62(18)：475-480．

(LI R，SHEN H D，FENG C H，etal．A novel solute redistribution model for cellular automaton and its validification[J]．Acta Phys Sin，2013，62(18)：475-480．)

[22] 孙东科，朱鸣芳，杨朝蓉，等．强制对流和自然对流作用下枝晶生长的数值模拟[J]．物理学报，2009，58(13)：285-291．

(SUN D K，ZHU M F，YANG C R，etal．Modeling of dendritic growth in forced and natural convections[J]．Acta Phys Sin，2009，58(13)：285-291．)

Simulation of Dendritic Morphology and Constituent Distribution of Al-4.7%Cu Alloy Under Convection

ZHOU Jingchao, LI Ri, YANG Yingying， ZHAO Chaoyang

(School of Materials Science and Engineering, Hebei University of Technology, Tianjin 300130, China)

A new two-dimensional modeling approach combining the cellular automaton(CA) and the lattice Boltzmann model(LBM) was developed to simulate heat transport, fluid flow, solute diffusion, and dendritic growth in the process of the Al-4.7%Cu solidification of the single-phase solid solution alloy. And the changes of dendritic morphology and constituent under convection were analyzed. The present model improved the solutal distribution approach at the solid-liquid (S/L) interface, which made the change of solute more consistent with the actual transport. The simulation results demonstrate that dendritic morphology is strongly influenced by forced convection, comparing with that without accounting for convection. Under the forced convection, the dendrite grain sizes tend to be similar; the constituent in the interdendritic region is more homogeneous; and the composition in the whole solidification region exhibits a certain gradient trend from upstream to downstream.

alloy solidification; microstructure simulation; CA-LBM; constituent distribution; dendritic morphology

(责任编辑：徐永祥)

2016-03-22；

2016-04-09

国家自然科学基金(51475138)；国家重点基础研究发展计划(2011CB610402)

李日(1966—)，男，博士，教授，研究方向为铸造CAD/CAE，(E-mail)sdzllr@163.com。

10.11868/j.issn.1005-5053.2016.4.001

TG146.2

A

1005-5053(2016)04-0001-09