变幅杆斜槽参数对纵弯振动系统的影响

段　鹏， 焦　锋， 赵　波， 牛　赢

(河南理工大学 机械与动力工程学院， 河南 焦作 454000)



变幅杆斜槽参数对纵弯振动系统的影响

段鹏， 焦锋*， 赵波， 牛赢

(河南理工大学 机械与动力工程学院， 河南 焦作 454000)

为了实现超精密切削，设计了二维纵弯超声振动系统中变幅杆的结构。通过分析开斜槽变幅杆的结构，理论上揭示了斜槽位置d、斜槽倾斜角α、斜槽长度l和斜槽间距h对变幅杆的谐振频率和纵弯两个方向振幅的影响规律。采用有限元动态数值模拟分析，得到不同斜槽参数情况下的谐振频率、振幅。发现随着α、l逐渐增大，模态频率呈现整体下降趋势，当α=45°时，弯曲振幅最大。在d=15 mm附近，振幅值最小，并且随h变大，振幅变小。利用正交参数的极差分析法得到斜槽各参数对谐振频率和振幅影响力度的主次。进一步通过实验，发现了随着α、h逐渐增大，谐振频率整体下降，且振幅随h的增大而减小。实验结果表明α通过对振幅的影响进而实现对切削力的控制，这与理论分析结果一致。

变幅杆；斜槽参数；谐振频率；纵弯振幅

PACS: 43.35.+d

二维超声振动切削通过特定的超声波振动系统给刀具施加超声振动，使刀具的切削刃在切削过程中附加一个椭圆轨迹的超声频振动。相较于一维超声振动切削，椭圆超声振动的引入使切削过程产生了根本性变化，带来了一系列优良的工艺效果，如降低切削力、提高表面加工质量、延长刀具寿命，其在超精密切削加工与难加工材料的加工中有着良好的应用前景[1-6]。

二维超声振动切削的关键是刀具超声振动系统的设计，目前国内外常采用的方法有两种。一种是通过给刀具施加两个相互垂直并有一定相位差的激励振动，在刀具的切削刃处合成椭圆振动。这种方法存在着电路复杂、振动系统结构复杂、体积大、调整困难和不利于生产应用等缺点[7-8]。另一种是单一振动源驱动的超声椭圆振动切削系统，单激励椭圆振动在椭圆形状以及振动方向调节上不如双激励系统的调节范围大，但是对于一些不需要经常调节的场合，如超声振动加工领域，是一种很好的应用选择[9-10]。

国内外研究表明，单激励椭圆振动系统振动轨迹产生的必要条件(即两个模态响应之间的相位差)是由于系统的结构不对称性造成的，通过调节激励频率和激励的位置可以改变椭圆振动轨迹的长短轴方向以及椭圆轨迹的大小。单激励椭圆振动系统在单一外部激励下(如纵向振动激励、扭转振动激励等)由于结构不对称等原因会存在两个对应相邻振动模态的激励分量，同时，单一外部激励的频率处于两个相邻振动模态固有频率之间[9]。而不对称结构的几何形状及位置对单激励椭圆振动系统的影响机理以及其对振动轨迹的影响则少有研究。本文利用理论推导、有限元分析与实验验证相结合的方式，研究不对称结构——斜槽的几何形状及位置对振动系统中变幅杆的频率和振幅的影响，寻找其中的影响规律。对斜槽的几何参数进行了优化，可得到超精密加工所需的椭圆振动模式。

1　斜槽几何参数对纵弯椭圆振动系统影响的理论分析

1.1单激励纵向振动经斜槽结构分解为纵向振动与弯曲振动的理论分析

为实现单激励下的二维纵弯超声振动，在垂直于变幅杆截面的方向上施加一个简谐振动激励，利用变幅杆结构上的不对称性，将该激励分解为两个互相垂直方向上响应，通过对一些结构参数的调整，在变幅杆的另一端形成所需要的轨迹。变幅杆开斜槽就是实现单激励二维超声振动的常见方式，考虑斜槽几何参数对纵弯振动的影响，对变幅杆开斜槽，如图1所示。

图1　变幅杆上的斜槽结构

变幅杆上存在斜槽的结构被分割成若干个倾斜的矩形薄板。斜槽的左右两部分由这些与轴线成α角倾斜的矩形板相连接,矩形板的厚度h是相临两个槽之间的距离,长度为l，模型如图2所示。在小变形假设下认为矩形板左连接处的转角为零，支承方式简化为固定端[11]。

图2　矩形薄板

考虑振动系统的结构和换能器对变幅杆的约束，设变幅杆的左端面固定端只有沿纵向，即图1中的x方向振动位移u(x)。薄板上分布载荷q(x1,y1)，振动位移沿y1方向不变化，而只沿x1方向变化，且沿y1方向两条边的边界支承条件不变，则矩形板的挠度w只是x1的函数，即

w=w(x1)。

(1)

斜槽结构两端截面上的内力被分割，作用线不重合，从而产生了合力偶矩M，其与单激励纵向振动同频率、同相位变化，这个周期变化的合力偶矩就是弯曲振动的激励源。则合力偶矩M为

M=F·lsinα,

(2)

F为作用在斜槽结构两端截面上的内力，即

(3)

式中，E为变幅杆材料的弹性模量，v为泊松比。则力偶矩M为

(4)

在力偶矩M作用下，挠度很小，因此挠度微分的平方项(即非线性项)可忽略不计，小挠度板的控制微分方程为

D22w=0。

(5)

式中，D=Eh3/[12(1-v2)]，为板的抗弯强度。联立(1)和(5)式，假设

(6)

(7)

当变幅杆长度l0=λ/2=C/(2f),即为半波长时，有

u(x)=Acos(kx)ejωt。

(8)

式中:A为单激励纵向振动的振幅，k=ω/C,ω为纵向振动的圆频率，C为变幅杆材料的纵波声速，λ为纵波波长，f为纵向振动的频率。

将(8)式代入(7)式中，得到薄板绕度w，沿x方向与y方向分解w，得到板右端面沿x方向与y方向的振动位移分别为

μ(x1)x1=l=u(x)x=d+w·sinα=

v(x1)x1=l=w·cosα=

(10)

y方向的振动位移v相对于变幅杆的轴线是一弯曲振动，其幅值与斜槽的长度l的三次方成正比、斜槽间距h的平方成反比，并随着倾斜角a及其在变幅杆上的位置d而变化。使斜槽的位置d靠近单激励纵向振动的波节点处，cos(kd)趋向于0，sin(kd)趋向于1，弯曲振动的幅值随即增大。随着斜槽的位置d远离单激励纵向振动的波节点处，cos(kd)趋向于1，sin(kd)趋向于0，x方向振动位移μ的幅值随即增大。斜槽的位置d在变幅杆近右端不变时，随着斜槽的长度l的变大、斜槽间距h的变小，倾斜角α的变大，振动μ的幅值变大。

1.2开斜槽结构变幅杆的纵向振动与弯曲振动的共振频率

由于斜槽的影响，变幅杆纵向振动和弯曲振动的共振频率相对于未开槽时将产生偏移。

1.2.1纵向振动的共振频率未开槽前，变幅杆的应力应变方程为

(11)

由于斜槽的影响,斜槽部分的纵向刚度减弱,在相同应力作用下，斜槽部分的变形增大，等同于这一部分材料的弹性模量变小了，此时的应力应变方程为

(12)

联立(8)、(9)、(11)和(12)式，得开槽后变幅杆的弹性模量Ec为

(13)

lcosα/c=lc/Cc,

(14)

得lc为

(15)

变幅杆开槽后变化长度ld为

ld=lo+lc-lcosα,

其中lo为变幅杆原长。利用knld=(2n-1)π/2,n=1，2，3…，即可取求变幅杆的纵向共振频率,即

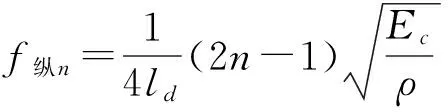
(16)

1.2.2弯曲振动的共振频率杆的弯曲振动方程[12]为

(17)

式中，K2=r2/4,C2=E/ρ,r为变幅杆半径。

可得频率方程

(18)

(19)

式中，设β=ωld/γ，用简正值βn(n=1，2，3，…)代表β的一系列值。

应用分解后的变幅杆纵向振动和弯曲振动的位移函数，求出弯曲振动共振频率与纵向振动共振频率相近时的变幅杆结构，这是实现纵弯复合振动的先决条件。

2　开斜槽变幅杆纵弯振动的有限元分析

纵弯振动系统由超声波发生器、超声波换能器、变幅杆与刀具四部分组成。超声波发生器是利用传统的220 V交流电压经过整流、滤波转换到功放电路进行信号放大，最后输出高频高压的交频振动电压加到超声换能器两端。换能器的作用就是通过压电片，将交频振动的电压转换成压电片沿纵向高频伸缩，从而辐射出所需频率的超声振动能，由换能器输出端输出的超声波频率很高，振幅很小，只有2～5 μm，而超精密加工，刀具的振幅一般都在5 μm左右。为此，超声波经过变幅杆的传递，振幅并未放大。

为配合超精密加工，本文设计的变幅杆谐振频率在35 KHz附近，振幅为5 μm，根据计算可以得到变幅杆基本尺寸如图3所示，法兰盘的位置就是振动节点。

图3　开斜槽变幅杆的结构模型

采用有限元的方法，对变幅杆进行模态分析与瞬态动力学分析，影响谐振频率和振动位移的斜槽参数包括斜槽与轴线的夹角α、斜槽距离节点的距离d、斜槽与斜槽之间的距离(板厚)h、斜槽长度l。考虑变幅杆的直径和材料的强度，变幅杆开有5个斜槽，宽度b=1.2 mm。在分析过程中，所用参数单位均为国际标准单位，变幅杆材料为45#钢。

2.1斜槽参数对纵向与弯曲振动影响的有限元分析

改变单个斜槽参数，进行模态分析，分别获得开斜槽变幅杆的模态频率，采用35 KHz附近的谐振频率，对变幅杆进行瞬态动力学分析，分析单个斜槽参数对纵向与弯曲振动的影响。图4为斜槽参数d=20 mm,h=1 mm,l=7 mm，α=45°的变幅杆有限元分析模型。

图4　开斜槽变幅杆的有限元分析模型

当斜槽参数d=20 mm，h=1 mm，l=7 mm，α=30°、45°、60°时，绘出变幅杆的频率曲线如图5a所示。从图中可以看到，随着开槽角度α逐渐增大，其模态频率在相同模态阶数下明显呈现出整体下降趋势。当斜槽参数h=1 mm，l=7 mm，α=45°，d依次选取10、15、20 mm时，绘出变幅杆的频率曲线如图5b所示。从图中可以看到，随着d逐渐增大，其模态频率在相同模态阶数下没有统一的变化规律。当斜槽参数d=20 mm，l=7 mm，α=45°，h依次选取1、1.2、1.4 mm时，绘出变幅杆的频率曲线如图5c所示。从图中可以看到，随着板厚h逐渐增大，其模态频率在相同模态阶数下变化平缓。当斜槽参数d=20 mm，h=1 mm，α=45°，l依次选取7、9、11 mm时，绘出变幅杆的频率曲线如图5d所示。从图中可以看到，随着斜槽长度l逐渐增大，其模态频率在相同模态阶数下呈现出整体下降趋势。如图5所示，35 kHz附近的谐振频率因斜槽参数发生了一定偏移，但随着参数的变化，其变化平缓。

进一步研究变幅杆输出端的振动响应情况。通过ANSYS中的函数编辑器来编辑位移函数u(x)=Asin(2πft+Φ)，将其施加到变幅杆与换能器连接的端面。其中幅值A为5 μm，频率f取各变幅杆在35 kHz附近的谐振频率，初始相位角Φ定为0。求解完成后，在变幅杆输出端面预安装刀具位置处提取节点随时间变化的X、Y方向的位移响应，其中UX代表轴向(即纵向)位移，UY代表径向(即弯曲方向)位移，得到各变幅杆的位移响应(即振幅)，根据各变幅杆在UX和UY方向上的振幅数据，利用Origin软件绘出振幅曲线，如图6所示。

图5　不同斜槽参数时的频率曲线

图6　不同斜槽参数时的振幅曲线

从图6a可以看出，随着开槽角度α的变大，弯曲振幅随之变大，当α=45°时，弯曲振幅最大，超过45°时，弯曲振幅开始变小；纵向振幅受斜槽角度α的影响较小。从图6b可以看出，在d=15 mm的附近，振幅值最小。纵向振幅受斜槽参数d的影响较大，越靠近节点(d值越小)，纵向振幅越大；弯曲振幅受斜槽参数d的影响较小。从图6c可以看出，随着板厚h的变大，振幅明显变小。上述三参数对振幅的影响与理论推导的表达式(9)、(10)分析结果基本一致。从图6d可以看出，随着斜槽长度l的变大，纵向振幅明显变大，此与理论推导的表达式(10)分析结果基本一致，而弯曲振幅先变大再变小，且变化程度不大，与理论推导的表达式(9)分析结果不同，这是因为斜槽长度l大到一定程度，施加在变幅杆左端的位移激励的传导受阻变大，振幅变小。

2.2斜槽参数对纵向与弯曲振动影响的有限元分析

采用如表1所示的四因素三水平正交参数进行仿真，分析多个斜槽参数对纵向与弯曲振动的交互影响。首先进行模态分析，获得不同模态阶数下模态频率，在35 kHz附近，选取符合设计要求的谐振频率，如表1所示。通过极差R1的分析，影响谐振频率偏移的主、次顺序分别为：h>d>α>l。

对变幅杆进行瞬态动力学分析，在变幅杆输出端面预安装刀具位置处提取节点随时间变化的X、Y方向的位移响应，得到各变幅杆的位移响应(即振幅)，如表1所示。通过极差R2的分析，影响轴向(即纵向)位移的主、次顺序分别为：d>l>α>h，随着d的变大，斜槽远离节点位置，纵向位移UX开始变小，与理论推导的表达式(10)分析结果相一致。通过极差R3的分析，影响径向(即弯曲方向)位移的主、次顺序分别为：α>h>d>l，随着开槽角度的增大，弯曲位移UY也随之变大，当α>45°时，弯曲位移UY开始变小。当α不变时，随着板厚h的减小、开槽长度l增大，弯曲位移UY也随之变大，与理论推导的表达式(9)分析结果大体一致。

表1 正交斜槽参数谐振频率与预装刀具位置点位移仿真结果及四因素三水平极差分析表

3　试验分析

在变幅杆的有限元分析过程中，各材料参数选取的是标准值。但实际上，从材料到加工存在很多不确定因素，导致最终结果跟理想状态有一定差距。为验证有限元分析的结果，发现斜槽参数对变幅杆的振动特性的影响，现对变幅杆的基本性能进行测试。斜槽角度α依次选用30°、45°和60°，改变板间厚度，每个角度分别有两个斜槽和三个斜槽，其中斜槽长度l=7 mm，斜槽宽度b=1.2 mm，斜槽中心距端面距离d=13 mm。

3.1阻抗测试

为验证前面有限元对变幅杆的模态频率的分析，在加工后对变幅杆同换能器组成的连接系统进行阻抗分析。与有限元分析值进行对比，对相同变幅杆，实验测得谐振频率与模态分析得到的频率有500 Hz以内的误差，仍在可接受的范围。实际谐振频率的变化趋势和模态频率变化趋势基本一致，如图7所示，这也对有限元的模态分析的结果进行了验证。

图7 实测谐振频率和模态频率对比曲线图

3.2振幅测试

利用ZJS-500N型超声波发生器和激光位移传感器对变幅杆的纵弯振动振幅进行测试。

在纵振方向(UX)实测值要小于仿真值，在弯曲方向(UY)实测值要稍大于仿真值，如图8所示。一方面可能是由于斜槽部分对振动方式会发生转换，削弱了纵向振幅，增强了弯曲振幅。另一方面可能是由于部件的结合改变了振动系统的约束条件。

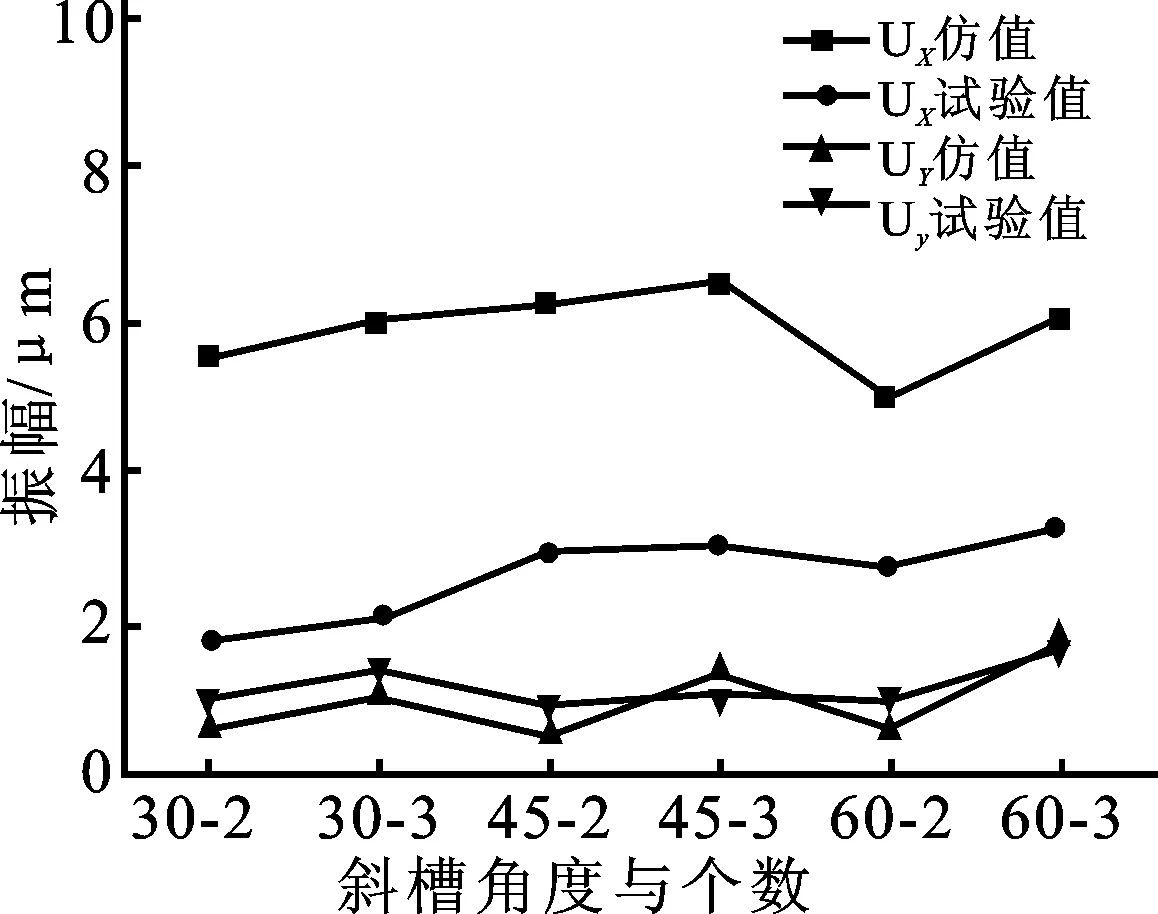
图8　实测振幅和仿真振幅对比曲线图

在二维振动系统下，使用斜槽参数d=20 mm，h=1 mm和α=30°、45°的变幅杆，采用PCBN刀具对硬质合金YG15材料进行切削试验。切削速度v=20 m/min，切削量ap=50 μm，进给速度f=0.05 mm/r。切削力的大小能够直观地反映加工过程的变化和预测加工结果。利用测力仪采集切削力的数据，主切削力FP、背向力Ft、进给力Ff大小如图9所示。

图9切削力波形图

Fig.9The waveform of cutting force

从图9可得，椭圆振动辅助切削的切削力比传统切削的切削力有不同程度的减小，这是因为椭圆振动辅助切削增大了切削工作前角，反转了切屑与前刀面的摩擦力方向，促进了切屑的流动。对比使用30°和45°这两种变幅杆装置条件下的切削力，随着α变大，其呈现下降的趋势。这是由于使用45°变幅杆时，振幅差值(UX-UY)小于使用30°变幅杆时的振幅差值，使的切削工作前角更大，弯曲振幅UY远大于30°变幅杆的，导致反转切屑与前刀面摩擦力方向的时间段变长，使得切削力下降的更多。

4　结论

根据理论推导和有限元分析，可以得到以下结论：斜槽参数α、d对纵向与弯曲两方向的振幅有较大的影响；而l与h相互关联，影响纵向振动激励的传导性。设计变幅杆时，通过开斜槽，可实现加工系统的二维椭圆超声振动，调整变幅杆上斜槽结构的参数α与d，影响刀尖的振幅与运动轨迹，从而满足超精密加工所需的椭圆振动模式。

[1] SHAMOTO E, MORIWAKI T. Study on elliptical vibration cutting[J]. Annals of the CIRP, 1994, 43(1): 35-38.

[2] MORIWAKI T, SHAMOTO E. Ultrasonic elliptical vibration cutting[J]. Annals of the CIRP, 1995, 44(1): 31-34.

[3] SHAMOTO E, MORIWAKI T. Ultraprecision diamond cutting of hardened steel by appling elliptical vibration cutting[J]. Annals of the CIRP, 1999, 48(1): 441-444.

[4] NATH C, RAHMAN M, NEO K S. A study on ultrasonic elliptical vibration cutting of tungsten carbide[J]. Journal of Materials Processing Technology, 2009, 209(9): 4459-4464.

[5] SUZUKI N, HARITANI M, YANG J, et al. Elliptical vibration cutting of tungsten alloy molds for optical glass parts[J]. Annals of the CIRP, 2007, 56(1): 127-130.

[6] 季远, 李勋, 张德远. 超声椭圆振动精密切削[J]. 航空制造技术, 2005, (4):92-95.

[7] AOYAGI M, T0MIKAWA Y, TAKANO T. Ultrasonic motors using longitudinal and bending multimode vibration with mode coupling by externally additional Asymmetry or internal nonlinearity[J]. Japanese Journal of Applied Physics. 1992, 31(9B): 3077-3080.

[8] AOYAGI M, TSUCHIYA S, T0MIKAWA Y. Trial production of an ultrasonic motor using longitudinal and torsional vibrations of rod vibrator driven by piezoelectric plates inserted in its axial direction[J]. Japanese Journal of Applied Physics, 1997, 36(9B): 6106-6109.

[9] 季远. 单激励超声椭圆振动系统及其在精密振动切削中的应用研究[D]．北京：北京航空航天大学机械工程及自动化学院，2004.

[10] 李华，张德远. 新型单激励椭圆超声振动切削系统的研究[J].中国机械工程，2005, 16(22): 1983-1990.

[11] 曲庆璋，章权，季求和，等. 弹性板理论[M].北京：人民教育出版社，2000: 27-40.

[12] 林仲茂. 超声变幅杆的原理和设计[M]. 北京：科学出版社，1987: 40-52.

〔责任编辑 李博〕

Influence of parameters of the chute on longitudinal-flexural vibration system

DUAN Peng, JIAO Feng*, ZHAO Bo, NIU Ying

(School of Mechanical and Power Engineering, Henan Polytechnic University,Jiaozuo 454000, Henan， China)

In order to realize ultraprecision cutting, the amplitude amplifier horn structure of longitudinal-flexural vibration system is designed. By analysis of the horn structure, the influence rule of location (d), angle of inclination(α), length (l) and spacing (h) of chutes on the resonance frequency of the horn and the amplitude of the longitudinal-flexural vibration were revealed theoretically. Under different parameters of chutes, the resonance frequency，amplitude, and rule that modal frequencies are obtained.The results show that withαandlincreased gradually, bending amplitude was maximum whenα=45° and amplitude value was minimum in the vicinity ofd=15 mm.As chute spacinghbecame larger, the amplitude became smaller were achieved by means of FEA method.The primary and secondary influence of chute parameters on resonance frequency and amplitude was obtained by range analysis of orthogonal parameters. Through experiments, it was discovered that withαandhincreased gradually, resonant frequency overall declined.Ashincreased, amplitude became smaller, and cutting force was changed through influence ofαon amplitude. The results of experiments are consistent with the theoretical analysis.Keywords: amplitude amplifier horn; chute parameters; resonance frequency; amplitude of longitudinal-flexural vibration

1672-4291(2016)04-0049-07

10.15983/j.cnki.jsnu.2016.04.246

2015-12-28

国家自然科学基金(51075127)

焦锋，男，教授，博士生导师。E-mail:jiaofeng@hpu.edu.cn

TP273；TB552；O242.21

A