矩形压电陶瓷超声换能器的弯曲振动

唐一璠， 林书玉

(陕西师范大学 物理学与信息技术学院, 陕西 西安 710119)



矩形压电陶瓷超声换能器的弯曲振动

唐一璠， 林书玉*

(陕西师范大学 物理学与信息技术学院, 陕西 西安 710119)

利用等效弹性法分析了矩形陶瓷超声换能器在不同条件下的弯曲振动，分别对四边简支条件下的特征频率和边界自由与边界固定条件下的特征频率进行曲线拟合,得出矩形压电陶瓷超声换能器在边界自由与边界固定条件下弯曲振动特征频率的拟合公式。利用有限元分析软件Comsol对得到的拟合公式进行验证，验证结果表明边界自由与边界固定条件下矩形压电陶瓷超声换能器的特征频率与拟合公式计算出的特征频率有很好的一致性。

压电陶瓷； 弯曲振动； 特征频率； 有限元分析

PACS: 43.35.+d

超声换能器是进行能量转换的器件，它能够实现机械能与电能的相互转换。压电陶瓷超声换能器在水声换能器、空气超声换能器及压电陶瓷滤波器中有非常广泛的应用,同时也被应用于石油声波测井中,用来获取地层的横波等信息[1-2]。随着超声技术的快速发展，对超声换能器提出了新的要求，要求超声换能器和辐射器具有大辐射面、大功率、多频等功能[3-5]。

研究压电陶瓷振子各种振动模式是设计压电换能器的基础[6-7]。弯曲振动是一种间接产生的振动模式,弯曲振动同时存在伸长和缩短这两种形变,比扭转振动和纵向振动更复杂。在实际应用中，不能简单地认为压电陶瓷振子都工作于单一的振动模式，事实上压电陶瓷振子的振动模式是不同方向振动模式之间的相互作用[8-9]。

对于圆盘薄板压电陶瓷超声换能器的弯曲振动，国内外学者已经进行了比较系统的理论研究，瓦奈脱(Wollett)应用瑞利(Rayleigh)法对弯曲圆盘换能器的工作特性进行了研究,所得结果较为简单且与实际测试结果符合良好,因此具有较高的实用价值[10]。但是，对于矩形压电陶瓷换能器的研究，因为找不到满足边界条件的解，所以矩形压电陶瓷超声换能器弯曲振动的研究并不完善。文献[11]曾经对矩形陶瓷超声换能器进行过研究，但是发现在自由边界条件下得到的特征频率方程式的解只能算出i=0，j≠0或j=0，i≠0的特征频率，当i和j同时不为零时特征频率方程式的解与实验结果不符。对于四边简支矩形压电陶瓷超声换能器的弯曲振动，可以给出其精确解，但是对于边界自由和边界固定的弯曲振动，找不到满足边界条件的解。

等效弹性法是研究弹性体耦合振动的一种分析方法,即对于材料均匀的弹性体,在不考虑剪切形变，只考虑伸缩形变的条件下其振动能够看成由两个相垂直的纵向振动和径向振动耦合而成，并且在不同方向的振动可以看作有不同的等效弹性常数， 即等效杨氏模量。在此条件下，该耦合振动由两个一维振动来表示，而从整体看，这两个等效振动则是通过耦合系数构成整个弹性体的耦合振动。本文利用等效弹性法理论[12]对矩形陶瓷超声换能器在不同条件下的弯曲振动进行了研究，利用矩形压电陶瓷超声换能器四边简支的精确解，得出了不同尺寸下的特征频率，再利用有限元分析方法Comsol对边界自由与边界固定条件下的矩形压电陶瓷超声换能器进行了模拟, 并利用四边简支的特征频率分别对边界自由与边界固定条件下弯曲振动的特征频率进行曲线拟合,得出矩形压电陶瓷超声换能器边界自由与边界固定条件下弯曲振动特征频率的两个拟合公式。

1　弯曲振动矩形陶瓷超声换能器的共振频率方程以及位移分布

图1为矩形压电陶瓷振子与矩形薄板几何示意图，其中L、W、H分别为长度、宽度、厚度。极化方向相反时可以用串联的方式，反之可以用并联的方式接入电源。对于串联型矩形压电陶瓷超声换能器，当上板电极为正、下板电极为负时，通过逆压电效应，上片伸长下片缩短，产生凸形弯曲形变；反之产生凹形弯曲形变。

图1　矩形压电陶瓷振子的几何示意图

在以下分析中，只考虑薄板的长度及宽度远大于厚度的情况，根据弹性力学中薄板的小饶度弯曲振动理论，其应变可表示为

(1)

(2)

(3)

上式中u=u(x，y，z)为板的横向位移，同时矩形压电陶瓷超声换能器的压电方程可写为

(4)

(5)

(6)

(7)

(8)

此时薄板的弯曲振动可以等效为绕x轴和y轴的两个独立的弯曲振动，此时板的横向位移可以近似用(9)式表示，即

u=u(x,y,t)=ux(x)uy(y)exp(jωt)。

(9)

1.1矩形薄板绕y轴的弯曲振动

在长度方向的应力可以表示为

(10)

在x为常数的截面上，由σx产生的弯矩可表示为

(11)

其中W为矩形板的宽度,把(10)代入(11)式积分后可得

(12)

在不计转动的条件下，根据力矩平衡方程可得

(13)

则矩形薄板绕y轴的弯曲振动方程为

(14)

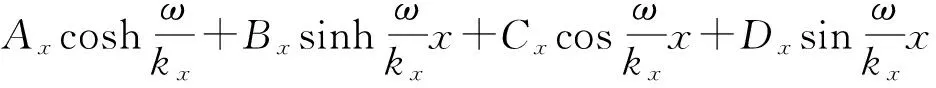
(15)

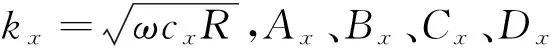
1.2矩形板绕x轴的弯曲振动

在y为常数的截面上，由σy产生的弯矩可表示为

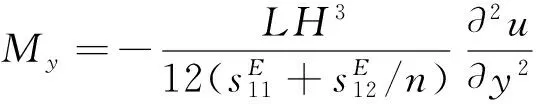
(16)

在不计转动的条件下，根据力矩平衡方程可得

(17)

则矩形薄板绕x轴的弯曲振动方程为

(18)

则矩形薄板绕x轴弯曲振动的位移分布为

(19)

2　矩形压电陶瓷超声换能器四边简支条件下的特征频率

对于四边简支的矩形压电陶瓷超声换能器，满足其边界条件为横向位移及弯矩等于零，利用(15)和(19)式可得决定振子两个等效弯曲振动的共振频率方程式为

(20)

(21)

(22)

(23)

由此可得关于机械耦合系数及x和y方向弯曲振动共振频率的方程式为

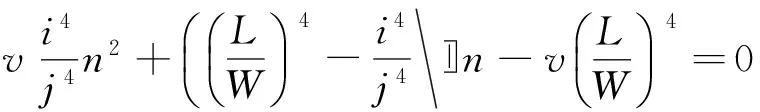
(24)

(25)

由(25)式可得矩形薄板弯曲的共振频率，根据

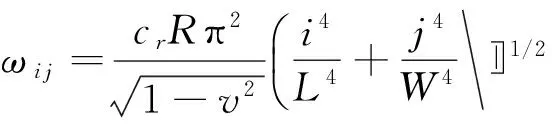
(26)

3　矩形压电陶瓷超声换能器边界自由条件下的特征频率

在矩形压电陶瓷超声换能器自由边界的特征频率分析中，由于没有泊松效应的耦合振动,只是把矩形压电陶瓷超声换能等效为绕x轴和y轴的两个独立的弯曲振动，考虑到弯曲振动中x方向与y方向弯曲振动的相互作用，可以利用矩形压电陶瓷超声换能器四边简支共振频率方程(26)式，得到四边简支条件下矩形板弯曲振动共振频率的精确解，利用有限元分析软件Comsol模拟出不同尺寸下边界自由弯曲振动的特征频率,并利用Origin软件对四边简支条件下的特征频率和边界自由条件下的特征频率进行曲线拟合,得到矩形压电陶瓷超声换能器自由边界条件下弯曲振动特征频率的一个拟合公式，即

(27)

图2是利用Comsol模拟边界自由以及用拟合公式计算出来的压电陶瓷弯曲振动的(1.1)阶模态的特征频率，其中实线为利用有限元分析软件Comsol模拟出自由边界条件下(1.1)阶弯曲振动的特征频率,虚线为用拟合公式(27)计算出来的(1.1)阶模态压电陶瓷弯曲振动的频率。可以看出二者吻合较好。

图2　边界自由压电陶瓷的(1.1)阶模态的特征频率

图3是矩形压电陶瓷超声换能器在L=52 mm，W=20 mm，H=4 mm的(1.1)阶模态边界自由条件下弯曲振动的振动模态。其中浅色表示相对振动位移较小，深色表示相对振动位移较大，由图可知，矩形压电陶瓷超声换能器在x和y方向均有两条节线，3个峰值，特征频率为f=40 886 Hz。

图3　边界自由条件下压电陶瓷振子(1.1)阶模态的振动

4　矩形压电陶瓷超声换能器边界固定条件下的特征频率

利用矩形压电陶瓷超声换能器四边简支共振频率方程(26)式，得到四边简支条件下矩形板弯曲振动共振频率的精确解，利用有限元分析软件Comsol模拟出不同尺寸下边界固定弯曲振动的特征频率,并利用Origin软件对四边简支条件下的特征频率和边界固定条件下的特征频率进行曲线拟合,得到矩形压电陶瓷超声换能器固定边界条件下弯曲振动特征频率的一个拟合公式，即

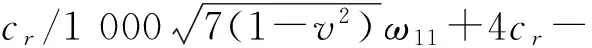
(28)

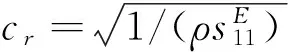
图4是利用Comsol模拟边界固定以及用拟合公式计算出的压电陶瓷弯曲振动的(1.1)阶模态的特征频率，其中实线为利用有限元分析软件Comsol模拟出固定边界条件下(1.1)阶模态弯曲振动的特征频率，虚线为用拟合公式(27)计算出的(1.1)阶模态压电陶瓷弯曲振动的频率。可以看出二者吻合较好。

图4　边界固定压电陶瓷的(1.1)阶模态的特征频率

图5是矩形压电陶瓷超声换能器在L=52 mm，W=20 mm，H=4 mm的(1.1)阶模态边界固定条件下弯曲振动的振动模态。其中浅色表示相对振动位移较小，深色表示相对振动位移较大，由图可知，矩形压电陶瓷超声换能器在x和y方向的边均为固定边界，特征频率为f=29 854 Hz。

图5　边界固定条件下压电陶瓷振子(1.1)阶模态的振动

5　结论

本文利用等效弹性法理论对矩形陶瓷超声换能器在不同条件下的弯曲振动进行了研究，得出矩形压电陶瓷超声换能器四边简支的精确解,利用有限元分析软件Comsol模拟出不同尺寸下边界自由和边界固定弯曲振动的特征频率,并利用Origin软件对四边简支条件下的特征频率和边界自由与边界固定条件下的特征频率进行曲线拟合, 得出矩形压电陶瓷超声换能器边界自由与边界固定条件下弯曲振动特征频率的两个拟合公式,并对得到的拟合公式进行验证。验证结果表明，拟合公式计算出的特征频率在边界自由和边界固定条件下矩形压电陶瓷超声换能器的特征频率符合良好。本文仅得出了矩形压电陶瓷超声换能器边界自由与边界固定条件下弯曲振动(1.1)阶模态共振频率的拟合公式,为了能使边界自由与边界固定条件下弯曲振动换能器更广泛地应用于生产生活中,我们在以后的工作中将拟合出它们的高阶共振频率计算公式。

[1] 林书玉.超声换能器的原理及设计[M].北京：科学出版社，2004: 142.

[2] 付琳,王东,王秀明.用ANSYS分析矩形压电陶瓷振子的振动模式[J]. 声学技术， 2011, 30(6): 313-314.

[3] LIN S Y. Analysis of the sandwich piezoelectric ultrasonic transducer in coupled vibration[J].The Journal of the Acoustical Society of America, 2005, 117(2): 653-664.

[4] NIEMCZEWSKI B. Observations of water cavitation intensity under practical ultrasonic cleaning conditions[J]. Ultrasonics Sonochemistry, 2007, 14: 13-18.

[5] PESHKOVSKY S L, PESHKOVSKY A S. Matching a transducer to water at cavitation acoustic horn design principles[J]. Ultrasonics Sonochemistry, 2007, 14: 314-322.

[6] LIN S Y，WANG S J. Radially composite piezoelectric ceramic tubular transducer in radial vibration [J]. IEEE Transactions on Ultrasonic Ferroelectrics and Frequency Control, 2011, 58: 2492-2498.

[7] CHACON D, RODRIGUEZ-CORRAL G, GAETE-GARRETON L, et al. A procedure for the efficient selection of piezoelectric ceramics constituting high-power ultrasonic transducers[J]. Ultrasonics, 2006, 44: 517-521.

[8] 黄磊落，朱秀丽，牛勇，等.二维振动方向变换器的耦合振动[J]. 压电与声光, 2008, 30(4): 425-427.

[9] 林书玉.超声技术的基石:超声换能器的原理及设计[J]. 物理, 2009, 38(3): 141-148.

[10] 周洪福.水声换能器及基阵[M].北京： 国防工业出版社， 1984: 110.

[11] 林书玉.压电陶瓷矩形薄板振子的弯曲振动研究[J].陕西师范大学学报(自然科学版), 1997, 25(1): 39-43.

[12] 徐芝纶.弹性力学[M].下册.北京：人民教育出版社，1982: 258-302.

〔责任编辑 李博〕

Rectangular bending vibration of the piezoelectric ultrasonic transducer

TANG Yifan, LIN Shuyu*

(School of Physics and Information Technology, Shaanxi Normal University,Xi′an 710119, Shaanxi, China)

Using the equivalent elastic method, the bending vibration of rectangular ceramic ultrasonic transducer under different conditions is analyzed.The characteristic frequencies of the four sides simply supported conditions are fitted.Under the condition of fixing boundary and free boundary, two fitting formulas of the characteristic frequency of the bending vibration of the rectangular piezoelectric ceramic ultrasonic transducer are obtained. Using the finite element analysis software Comsol to verify the obtained fitting formula, the results show that the characteristic frequency of rectangular piezoelectric ceramic ultrasonic transducer is consistent with the fitting formula.Keywords: piezoelectric ceramics; bending vibration; characteristic frequency; finite element analysis

1672-4291(2016)04-0044-05

10.15983/j.cnki.jsnu.2016.04.245

2015-06-09

国家自然科学基金(11174192,11374200,11474192)

林书玉，男，教授，博士生导师。E-mail:sylin@snnu.edu.cn.

O462.4

A