一维不连续映像动力学时间序列的复杂网络分析

路少怀， 杜如海， 屈世显

(陕西师范大学 物理学与信息技术学院， 陕西 西安 710119)



一维不连续映像动力学时间序列的复杂网络分析

路少怀， 杜如海， 屈世显*

(陕西师范大学 物理学与信息技术学院， 陕西 西安 710119)

利用复杂网络方法研究了一维不连续映像的动力学，建立了不同动力学状态时间序列相应的复杂网络。对于任意P周期吸引子，可以构成相互独立的P个全连接网络；对于混沌吸引子，可以构成许多分立的复杂网络。同时，讨论了系统所对应网络的连接密度、聚类系数、平均最短路径长度等特征量随控制参数变化的特征，分析了网络特征量与系统动力学之间的联系。结果发现:连接密度在不同周期吸引子间有不连续的跃变，在周期吸引子和混沌吸引子转变时出现不光滑变化；聚类系数和平均最短路径在周期吸引子与混沌吸引子间发生转变，并且在吸引子融合处均呈现不光滑转变。因此，可以用相应复杂网络特征量刻画不同动力学状态及指示其转变，并且当有吸引子共存出现时，这些量可以检出周期吸引子。

递归图； 复杂网络； 不连续映像； 动力学转变

PACS: 89.75.Hc, 05.40 Fb,05.60.-k

利用现代数据分析技术研究复杂动力学系统特征已受到研究者越来越多的重视[1-3]，其应用范围涉及许多科学领域，例如：天体物理学、经济学、生命科学等。 关联维数、李雅普诺夫指数、互信息等方法已被广泛运用[2-4]。 然而，这些方法需要使用很长的数据序列，而在分析具有较短时间序列的实际数据时，可能会导致不正确的结果。 因此，发展针对实际系统小数据时间序列特征的分析方法非常必要。

近年来，网络中小世界效应和无标度特性的发现引起了复杂网络研究的热潮。 典型的网络是由许多节点以及节点之间的连边组成。 节点用来代表真实系统中的不同个体，而边则用来表示不同个体之间的关系。 为了研究复杂网络的统计特征，人们提出了平均路径长度、聚类系数、连接密度、度分布等概念。 复杂网络作为一种新方法已被用于研究动力学系统的时间序列[5]。 在这类工作中，基于动力学状态的时间序列，利用所谓递归图方法直观表示系统的动力学特征, 并通过所谓递归矩阵建立不同时刻系统状态之间的联系，从而构建以动力学状态为节点的复杂网络。 利用复杂网络的局部和全局性质的特征量描述系统的动力学特征及不同动力学状态间的相互转变[6-9]。 基于该方法，可以获得大量有关系统动力学的信息，其优越性在于可以用来分析那些包含临界特征的短时间序列的非稳态实际数据。

在Marwan等人[5]的工作中，复杂网络方法的研究对象主要集中于连续映像。 然而，在许多实际系统中，例如：神经细胞[10]、心脏病[11]、张弛振子和冲击振子[12-13]、继电控制系统[14]、直流变换器等，其动力学往往表现出不连续变化，可以用不连续映像描述系统的动力学。 在这类系统中，由于边界碰撞分岔造成与处处光滑系统非常不一样的动力学行为，例如：V型阵发、多重魔鬼阶梯、吸引子共存、激变等。 因此，不连续映像中的动力学行为是一个非常重要的研究领域。 特别需要指出的是，在以往的基于复杂网络的研究中，尚未见到处理具有共存现象的例子。

在本文中，我们以一个一维不连续不可逆映像[15]为例，在不同动力学参数区间构建复杂网络，计算其相应的特征量，并以此作为揭示动力学状态及其转变的特征指标。

1 模型与方法

本文所使用的动力学模型是一维不连续不可逆映像，即

xn+1=fi(xn)=ki·xn+bi(i=1,2,3,4),

(1)

其中:

k3=0.307 055,b3=-0.530 165,x∈[xg,xF];

k4=0.405 507,b4=-0.201 586,x∈[xF,1]。

变量yb=b1-μ,yA=0.203 921,yC=0.46,yG=yA,xb=0.107 663,xg=0.35,xF=0.497 121,μ∈[0.025,0.06]为控制参数。 随着控制参数μ的变化，映像表现出丰富的动力学行为，图1为相应的分岔图。 图中显示，当μ<μ1时，只有5周期吸引子；当μ1≤μ<μ2时，5周期吸引子与11带混沌吸引子共存；当μ2≤μ<μ3时，只有5周期吸引子；当μ3≤μ<μ4时，5周期与6周期吸引子共存；当μ4≤μ<μ5时，周期6轨道经边界碰撞分岔转变为12带混沌吸引子，出现5周期吸引子与12带混沌吸引子共存；当μ5≤μ<μ6时，12带混沌融合转变为6带混沌，出现5周期吸引子与6带混沌吸引子共存；μ6≤μ，周期5轨道经边界碰撞分岔消失，仅存在混沌吸引子。 其中，μ1=0.028 79,μ2=0.030 40,μ3=0.039 56,μ4=0.045 06,μ5=0.050 11,μ6=0.051 14。

图1　模型的分叉图

下面叙述通过映像动力学状态的时间序列构造复杂网络的方法。 考虑一维动力学系统，设xi(i=1,2,…N) 为相空间中不同时刻的动力学状态，即离散时间序列。 据此可以定义如下递归矩阵R，其矩阵元可由下式得到

Ri,j=Θ(ε-d(xi-xj)),

(2)

其中:Θ(x)为阶跃函数;ε为距离阈值，在本工作中设为0.000 8;d(xi,xj)=|xi-xj|为状态xi和xj间的距离,若d(xi,xj)≤ε，Ri,j=1，反之，Ri,j=0。 显然，递归矩阵反映了第i个时间步时系统的状态与第j个时间步的状态在相空间的邻居关系。Ri,j=1表明两个状态在相空间互为邻居，Ri,j=0表明两状态在相空间中不相关。 如果将系统的状态xi看做节点，Ri,j=1表示状态xi和xj间有连边，Ri,j=0表示两个节点间没有连边。 因此，可以由系统的时间序列构建一个复杂网络。 显然，除对角元外递归矩阵就与复杂网络的邻接矩阵相应。 因此，移除递归矩阵中的主对角元素，即可得到一个无权无向网络的邻接矩阵A，其矩阵元为

Ai,j=Ri,j-δi,j(i,j=1,2,…,N),

(3)

其中，δi,j是克罗内克符号。 这样，就可以用复杂网络的语言描述系统的动力学特征。 基于邻接矩阵A，可以计算复杂网络的局部和全局特征量：节点度ki、连接密度ρ、聚类系数C和平均最短路径长度L。 节点的度定义为

(4)

N表示节点i邻居的数目。 节点的度是一个局部量，可以反映系统局部转态的相空间密度。 进一步，对所有节点的度求平均可以得到连接密度，即

(5)

该特征量反映动力学状态的相空间分布密度。 对于每个节点i可以定义聚类系数为

(6)

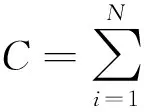
(7)

其中，di,j是指从节点i到节点j的最少连边数目。

2 结果与讨论

对于任意初值，我们选取6 000个连续时间步。 除去5 000个瞬态，则用于统计的时间序列长度为N=1 000。 我们计算了三个全局特征量随着映像控制参数μ的变化情况。 考虑到系统在一些参数区间中出现吸引子共存，不同的初值选择，对应不同的网络类型。 根据上一节所述的方法，对于一个周期P吸引子，其时间序列在相空间中仅存在P个相互独立的、且互不为邻的动力学状态，每个状态的邻居只能是其自身。 因此，通过周期P的时间序列可以构建P个相互独立的全连网络。 根据定义可以得到，周期吸引子网络的连接密度为ρ=(N/P-1)/(N-1)，聚类系数C=1，平均最短路径L=1。 对于混沌吸引子，尽管其动力学状态具有內禀随机性，但其在相空间的分布却是有结构的。 因而，通过其时间序列构建的网络不会是全连通网络，而是形成许多不同尺寸的独立网络、节点对或孤立节点(如图2所示)。 在这种情况下，我们不能像周期吸引子那样给出三个特征量的解析表达式，只能通过数值计算确定它们的数值。 混沌吸引子所构成网络的性质导致网络的连接密度和聚类系数小于周期吸引子情况下的值，而平均最短路径却要大于周期吸引子下的值。

图2　混沌吸引子对应网络拓扑结构示意图

首先，我们讨论网络的连接密度ρ随控制参数的变化。 图3显示，对于周期吸引子，连接密度是周期P与序列长度N的有理函数，当动力学从一个周期态向另一个不同周期态转变时将发生不连续的跃变，即Δρ=N(1/P2-1/P1)/(N-1)，例如图3中，μ∈[μ3,μ4]出现了周期5和周期6共存，我们观察到两者连接密度存在有限差值。 这表明，可以用连接密度的跃变明确地指示这种不同或者转变。 混沌吸引子对应着独立网络，因此相应的连接密度较小，随控制参数增加而呈连续变化的趋势，如图3中区域[μ1,μ2)和[μ4,0.060)所示。 在这两个区域中，随控制参数的增加网络连接密度减小，这是由于混沌带的宽度随控制参数的增加而增宽，从而造成落入任意状态xi的ε邻域中的状态数减少。 在这两个区域的边界上，即μ=μ1、μ2、μ4时，系统动力学行为发生了转变，因此相应的网络拓扑结构发生了突变，因此可以看到连接密度的不连续变化。 我们注意到，在μ=μ5时，网络连接密度有一微小的凸起。 这是由于该控制参量下发生了12带混沌融合为6带混沌吸引子，在融合点附近的一些原来不相关网络融合成较大网络，从而导致连接密度的些微增加。 我们将在后面的部分仔细讨论其机制。

需要特别指出，在出现共存的参数区域，例如[μ1,μ2)、[μ3,μ4)和[μ4,μ5)，不同的初值对应着不同的网络结构，我们在图3、图4和图5中将不同吸引子对应网络的特征值分别标出。 共存的周期5吸引子对应网络的特征值用虚线标出，共存的其他周期吸引子网络的特征值用实线标出，共存的混沌吸引子网络的特征值用数据点标出。

图3　连接密度随控制参数μ的变化

进一步讨论网络的聚类系数C随控制参数变化情况。 图4显示，周期吸引子对应网络的聚类系数均为1，与前面的预测结果一致。 因此，聚类系数C无法区分不同周期状态间的转变, 但可以明显区分周期状态和混沌状态间的转变。 在混沌状态，随控制参量增加落入任意状态邻域中的其他时刻状态的数目减小，相应网络节点间的连边减少，因此在图4的区域[μ1,μ2)和[μ4,0.060)中聚类系数随控制参数的增加而减小。 注意，在μ=μ5时聚类系数的变化曲线出现一个尖点，这是由于混沌带的融合造成了相应网络拓扑结构变化的结果。 因此，聚类系数C可以用来指示不同混沌吸引子间的转变。

图4　网络的聚类系数随控制参数μ的变化

最后，我们讨论平均最短路径长度L随控制参数的变化情况。 如图5所示，周期吸引子所对应网络的平均最短路径长度均为1，与解析结果一致，因而不能用于区分不同周期态之间的转变，但可以用于区分周期态和混沌态间的转变。 而当系统处于混沌状态时，L随控制参数的变化却出现比较复杂的情况。 在区域[μ1,μ2)和[μ4,μ5)，L随控制参数的增加而增大。 这样的变化是可以理解的，因为在这两个区域中的混沌带单纯由失稳的不动点造成，随着其宽度增加动力学状态在相空间中的分布范围扩大。 再考虑到平均最短路径长度L本质上是以ε为单位任意两个状态间距离的平均值，所以L随之增大。 这样，在μ=μ1、μ2、μ4各临界点上L出现非光滑变化。 因此，可以用它来指示周期态与混沌态间的转变。 有趣的是，当μ≥μ5时，平均最短路径却随控制参数的增加而减小。 显然，我们不能用前述原因解释。

图5　平均路径长度随控制参量μ的变化

图6中给出几个典型控制参数下系统处于12带混沌吸引子和6带混沌吸引子所对应复杂网络的拓扑图。 当μ=0.045 08时(见图6a)，系统刚刚通过边界碰撞分岔经由周期6转变为12带混沌状态，因此我们可以观察到12个独立的近乎全连的网络。 这时，网络的连接密度ρ小于周期6时的值(如图3所示)，聚类系数C略小于1(如图4所示)，而平均最短路径长度L略大于1。 当μ=0.048 00时(见图6b)，该12个网络拆分为许多较小的网络和数量较小的节点对和孤立节点。 这些较小的网络显著地偏离全连网络，因此其连接密度和聚类系数较前者小，而平均最短路径长度大于前者。 而当μ=0.050 00时，网络进一步碎片化(见图6c)，出现了较多的节点对和孤立点，因此，ρ和C进一步减小，而L进一步增大。 值得注意的是，当μ=0.050 11时系统的12条混沌带刚刚开始融合为6带混沌吸引子，从而引起了与融合点附近轨迹点相应的节点所属网络的融合, 见图6d中间区域的巨大网络；所以，我们在图5中观察到平均最短路径的突然跃升。 然而，与远离融合区的轨迹点对应的孤立节点和小网络的数目基本保持不变。 因此，我们可以在图3中观察该临界点处连接密度的些微抬升，在图4中观察到一个尖点。 当μ=0.053 00(见图6e)时，由于系统的动力学变得更加无序，图6d中央的巨大网络碎片化，孤立节点增多。 因此，平均最短路径减小。μ=0.056 00时(见图6f)，较大的网络进一步碎片化，孤立点进一步增多，因此平均最短路径长度则进一步减小。 因此，平均最短路径长度还可以明显地标示混沌融合。

图6 12带和6带混沌吸引子的网络拓扑图(x0=0.70)

Fig.6Network Topologies for band-12 and band-6 chaotic attractors(x0=0.70)

3 结论

本文基于复杂网络方法建立了一维不连续不可逆映像的时间序列所对应的复杂网络，计算了网络的平均最短路径长度、聚类系数、连接密度等特征量随控制参数的变化。 结果发现，当系统的动力学状态出现转变时，网络特征量具有明显的变化。 因此，可以用相应复杂网络特征量刻画不同动力学状态及其转变。 连接密度可以显著呈现周期吸引子与周期吸引子间的转变，以及周期吸引子与混沌吸引子间的转变。 而平均最短路径长度和聚类系数不仅可以标示上述转变，而且可标示混沌融合或激变。 当时间序列中存在周期吸引子和其他吸引子共存的情形时，通过判断全连网络的数目可以将周期吸引子检出。

[1] NORBERT M, NIELS W, UDO M, et al. Recurrence-plot-based measures of complexity and their application to heart-rate-variability data[J]. Physical Review E, 2002, 66: 0267028.

[2] NORBERT M, JONATHAN F D, YONG Z, et al. Complex network approach for recurrence analysis of time series[J]. Physics Letters A, 2009, 373: 4246-4254.

[3] KURTHS J, HERZEL H. An attractor in a solar time series [J]. Physica D, 1987, 25(10): 165-187.

[4] WOLF A, SWIFT J B, SWINNEY H L, et al. Determining lyapunov exponents from a time series[J]. Physica D, 1985, 16(3): 285-317.

[5] MARWAN N, ROMANO M C, THIEL M, et al. Recurrence plots for the analysis of complex systems[J]. Physics Report, 2007, 438(5/6): 237-329.

[6] ZHANG J, SUN J, LUO X, et al. Characterizing pseudoperiodic time series through the complex network approach[J]. Physica D, 2008, 237(22): 2856-2865.

[7] ZHANG J, SMALL M. Complex network from pseudoperiodic time series: topology versus dynamics[J]. Physical Review Letters, 2006, 96(23): 238701(1-4).

[8] YANG Y, YANG H. Complex network-based time series analysis[J]. Physica A, 2008, 387(10): 1381-1386.

[9] LACASA L, LUQUE B, BALLESTEROS F, et al. From time series to complex networks: the visibility graph [J]. Science Sessions, 2008, 105(13): 4972-4975.

[10] ALAIN V, DANTE R C, DONALD C M. Nonlinear dynamics and ionic mechanisms of excitation patterns in models of the cardiac myocyte[J]. Chaos, 1991, 244: 295-312.

[11] GRUDZINSKI K, ZEBROWSKI J J. Modeling cardiac pacemakers with relaxation oscillators[J]. Physica A, 2004, 336: 153-162.

[12] ALSTROM P, LEVINSEN M T. Phase-locking structure of "integrate-and-fire" models with threshold modulation[J]. Physics Letters A, 1988, 128: 187-192.

[13] GUAN S, WANG B H, WANG D K, et al. Dynamic interaction between discontinuity and noninvertibility: an analytical study[J]. Physical Review E, 1995, 52: 453-465.

[14] 赵益波, 罗晓曙, 汪秉宏,等.电压反馈型DC-DC变换器的稳定性研究[J]. 物理学报, 2005, 51(11): 5022-5026.

[15] QU S X, LU Y Z, ZHANG L, et al. Discontinuous bifurcation and coexistence of attractors in a piecewise linear map with a gap[J]. Chinese Physics B, 2008, 17(12): 4418-4423.

〔责任编辑 李博〕

Complex network analysis on the dynamical time series in one dimensional discontinuous map

LU Shaohuai, DU Ruhai, QU Shixian*

(School of Physics and Information Technology, Shaanxi Normal University,Xi′an 710119, Shaanxi, China)

The dynamics of one dimensional discontinuous map is investigated by the complex network approach. The complex networks are built for corresponding time series of different dynamical states. There arePindependent full-linked networks for an arbitraryP-period attractor and many independent complex networks of different sizes for a chaotic attractor. Meanwhile, the control parameter dependence of the link density, the clustering coefficient and the average length of the shortest paths for the complex networks are calculated and discussed. The correlation of these characteristic quantities with the dynamics of the system is analyzed. The result shows that the link density shows a discontinuous change for different periodic attractor and a nonsmooth change at the transition point between a periodic attractor and a chaotic attractor; the nonsmooth changes of the clustering coefficient and the average length of the shortest paths appear at the transition point between periodic and chaotic attractors, and the merging point of chaotic attractors, respectively. These phenomena imply that the characteristic quantities might be proper indexes to describe the dynamical states and exhibit their transitions. Moreover, they may help to check out the periodic attractors when they are coexistence with some other attractors.Keywords: recurrence plot; complex network; discontinuous map; dynamical transitions

1672-4291(2016)04-0038-06

10.15983/j.cnki.jsnu.2016.04.244

2016-01-27

国家自然科学基金(10875076)

屈世显，男，教授，博士生导师。E-mail: sxqu@snnu.edu.cn

O415.5

A