一类装配支线缓冲区配置的两阶段求解方法研究
2016-03-07李爱平张燕红刘雪梅徐立云
李爱平, 李 聪, 张燕红, 刘雪梅, 徐立云
(同济大学现代制造技术研究所,上海 201804)
一类装配支线缓冲区配置的两阶段求解方法研究
李爱平, 李 聪, 张燕红, 刘雪梅, 徐立云
(同济大学现代制造技术研究所,上海 201804)
研究一类装配支线的物料输送与缓冲问题,论文将传送辊道作为缓冲区的补充,构建基于辊道-缓冲区满足总装线产出率且最小化装配支线缓冲区总容量的优化模型.考虑到装配支线缓冲区容量配置与总线产出率之间不存在解析解,且装配支线缓冲区总容量一定时工位间不同缓冲区配置也影响着总线的生产.提出一种两阶段求解算法:第一阶段,采用遗传算法求解支线有限缓冲区总容量下的总装线最大产出率;第二阶段,根据Gershwin关于缓冲区-产出率的研究理论,获得总装线产出率所对应的装配支线缓冲区总容量,并进行支线缓冲区容量的合理分配.最后,通过案例分析验证该方法的有效性.
装配支线; 辊道; 缓冲区; 两阶段求解
缓冲区配置问题是生产线设计中的一个NP-hard问题,旨在寻找最优的缓冲区容量分配以达到特定的目标[1].张良安等[2]针对机器人装配的自动化生产线,建立生产线的可用度模型,运用遗传算法优化其缓冲区.高贵兵等[3]基于马尔可夫过程原理,建立混流装配线模型,并推导出装配线可用度与缓冲区容量之间的关系.宋士刚等[4]针对可重组制造系统的缓冲区配置,提出了缓冲区容量、机床可用度和任务需求率之间的函数关系,并通过粒子群算法以求解缓冲区的最小容量.MAGHSOUD等[5]针对异步式生产线提出缓冲区配置的多目标优化问题,运用遗传算法结合仿真实验以求解缓冲区容量的最佳配置.THOMAS等[6]针对异步式非平衡生产线进行缓冲区的容量分配,设置多组仿真实验,利用统计工具对生产线的产出率、空闲时间及平均缓冲区水平进行分析,并与平衡生产线进行比较研究.PRZEMYSLAW等[7]构建了带有返回路径的生产线缓冲区优化模型,采用改进模拟退火算法进行求解,以取得生产线收益的最大化.
在汽车发动机的生产中,其装配线经常是由一条总装线与多条装配支线构成,如缸盖、活塞连杆等部件在支线完成装配后,送至总线完成与发动机的合装.对于一类异步式装配支线的缓冲区配置问题,装配支线的主要特点是需满足总装线产出率的要求,装配支线的传输辊道也可以起到缓冲区的作用.本文针对该类总-支装配线,以满足总线产出率且最小化支线缓冲区容量为优化目标,采用两阶段求解算法,提高了求解的精准性和效率.
1 问题描述
产品的总装涉及到若干部件的装配过程,这些部件在装配支线上完成装配后,进入总装线完成产品的合装.如图1所示,图中总装线工位以{1,2,…,i-2,i-1,i}表示,装配支线工位用字母{1,2,…,m-2,m-1,m}表示,线边缓冲区以{B1,B2,…,Bm-1,Bm}表示,工位之间的传送辊道以辊道长度{L1,L2,…,Lm-2,Lm-1,Lm}表示.一般而言,装配支线的产出率必须能够保证达到总装线的产出要求,以避免出现总装线的停工.针对装配支线因设备故障等因素可能出现的产出率降低.传统做法是对其提前投料生产,并在总装线与装配支线间保持足够的缓冲以存放零部件.然而,装配支线的平均故障率会随着支线长度的增加而增加,导致两线间所需设置的缓冲区容量增大.
对于异步式装配线而言,工位之间物料的运送是通过辊道由人工启动和停止,辊道的运行是独立的.所以,对于该类装配支线缓冲区的配置,可以利用传送辊道来承担缓冲区的部分功能,而在辊道边建立各工位之间的缓冲区,这样,不仅提高了装配支线的产出率,而且提高了产出的稳定性,大大降低两线间的缓冲区容量.辊道一方面作为物料运输的通道,另一方面可以在一定程度上承担物料缓冲的功能.例如,物料放置在托盘,托盘放在辊道上,可根据辊道和托盘的长度来折算可容纳的托盘总数,即作为缓冲区的容量.在本文总-支线问题中,构建基于异步式装配线辊道-缓冲区的优化模型,以满足总装线产出率且最小化支线缓冲区总容量为求解目标,并对支线缓冲区容量进行合理配置.在保证总线产出的同时,降低了总、支线间缓冲区容量大小,提高了生产的稳定性.

图1 总装线与装配支线位置关系Fig.1 Position relationship between assembly line and the branch assembly line
2 数学模型
2.1 定义变量
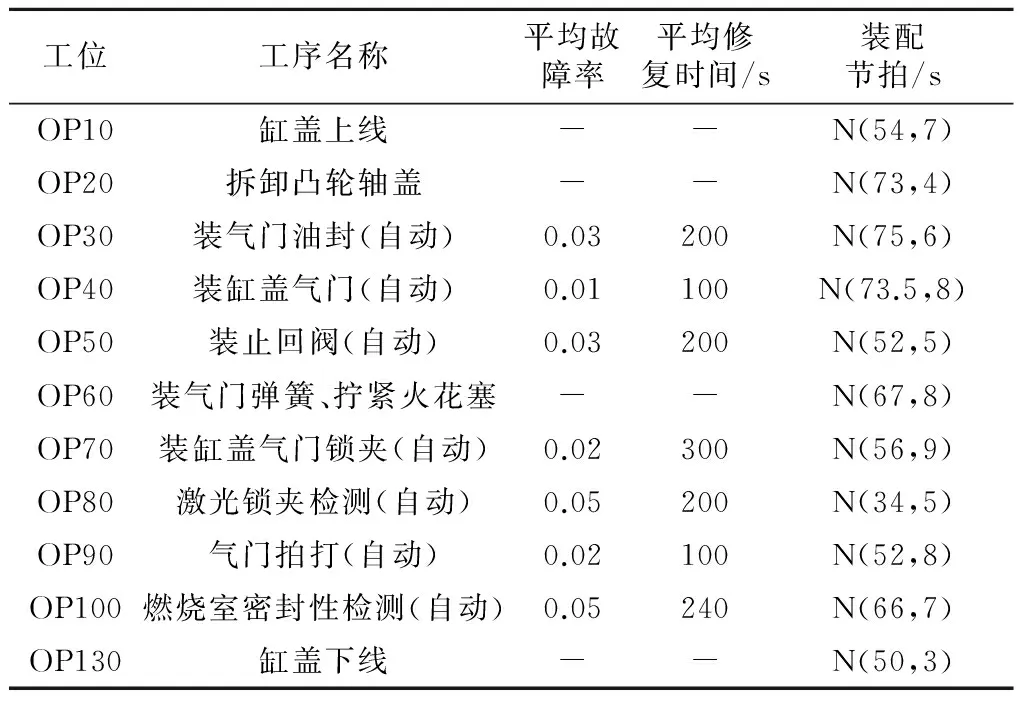
K为装配支线工位数;B为装配支线缓冲区容量配置的矢量;Bi为装配支线第i个缓冲区的容量(i=1,2,…,K-1);B′i为装配支线第i个辊道折算为缓冲区的容量(i=1,2,…,K-1);Li为装配支线第i个辊道的长度(i=1,2,…,K-1);P为托盘沿辊道方向的长度;f(B)为装配支线在缓冲区容量配置为B时的产出率;f*为装配支线的目标产出率,即总装线产出率;ui为装配支线第i个辊道旁允许设置的缓冲区最大容量(i=1,2,…,K-1);BT为装配支线缓冲区的总容量;fmax为装配支线缓冲区总容量所对应的最大产出率.
2.2 假设条件
(1) 缓冲区和辊道不会发生故障;
(2) 每个自动化设备均有可能发生故障,且设备MTBF和MTTR已知;
(3) 每个工位的操作时间符合随机分布,均值已知;
(4) 不考虑托盘在缓冲区中的物流时间;
(5) 第一个工位保证物料上线的及时,最后一个工位保证完成装配任务后物料及时下线.
2.3 数学模型
在满足总装线的产出率的前提下,装配支线利用辊道的辅助缓冲功能,配合线边缓冲区的配置以最小化支线缓冲区总容量,符合第2类缓冲区配置问题模型.
(1)
(2)
(3)
(4)
(5)
式(1)是问题目标函数,旨在最小化装配支线缓冲区总容量;约束(2)表明装配支线产出率不能低于总装线产出率;约束(3)表示传送辊道折算为缓冲区的容量大小;约束(4),(5)表示辊道旁缓冲区容量的取值范围.
3 算法求解
GERSHWIN在文献8中对缓冲区与生产线产出率之间的关系进行了分析和总结,指出生产线缓冲区的总容量与其最大产出率之间满足如图2所示的关系.

图2 缓冲区总容量(BT)与最大产出率(fmax)的关系Fig.2 Relationship between BT and fmax
由图2所示,缓冲区总容量在不大的情况下与生产线最大产出率存在近似线性的关系,论文在求解第2类缓冲区问题时,求解目标是在满足总装线产出率的情况下最小化装配支线缓冲区的总容量,由于不存在缓冲区容量配置与目标函数的解析式关系,所以在运用一阶段算法进行搜索时,势必会对不同缓冲区总容量BT下的不同配置进行搜索,从而增加了搜索范围.所以设计两阶段求解算法:如图3所示,算法执行前,首先选定初始BT,第一阶段,利用遗传算法求解BT所对应的fmax,如果fmax已充分接近总装线产出率f*,则输出BT即为装配支线最小缓冲区容量,否则进入第二阶段;第二阶段利用第一阶段所获得的点(BT,fmax)确定缓冲区总容量-最大产出率的线性方程,将总装线产出率f*代入方程以确定所对应的BT,返回给第一阶段.经过两阶段的循环迭代,最终确定装配支线最小缓冲区总容量.其中Bj-1和Bj表示迭代过程中前后两个点所代表的装配支线缓冲区总容量BT,后面会有详细说明.
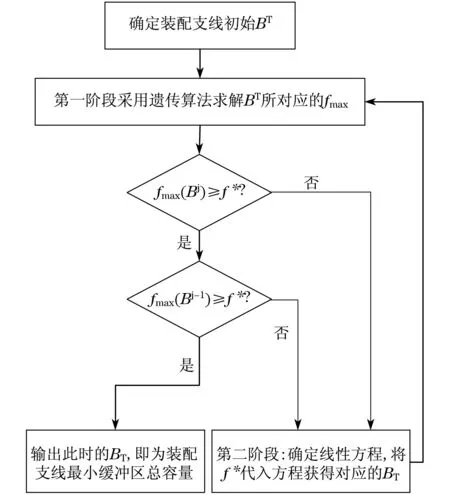
图3 两阶段算法求解流程Fig.3 Solving procedure of two-stage method
3.1 第一阶段求解
第一阶段求解问题描述如下.
Maximizef(B)
(6)
(7)
(8)
(9)
(10)
式(6)是目标优化函数,旨在求解装配支线的最大产出率;约束条件(7)表示缓冲区总容量等于一个特定值BT,由上述试验得出的缓冲区-产出率关系可知,有限缓冲区容量与其对应的最大产出率成线性关系,所以,获得特定BT对应的fmax,以便第二阶段算法的线性迭代;式(8)表示辊道折算为缓冲区的数目;式(9),(10)表示工位间缓冲区容量的取值范围.
采用遗传算法结合计算机仿真进行第一阶段问题的求解,遗传算法利用小区间生成法[9]生成初始种群,经过确定性选择、随机线性交叉[10]和变异进行种群迭代.
3.2 第二阶段求解
由于装配支线采用辊道连接前后工位,辊道能够承担部分缓冲区的功能.根据上述实验结果,采用线性迭代方法以获得最佳缓冲区总容量.
基于BT与fmax之间的单调线性关系,算法需要确定两个初始解B0、B1,对于B0,令B0=0,由仿真实验获得对应的fmax(B0),用上述遗传算法求解B1下的fmax(B1),根据两点(B0,fmax(B0))(B1,fmax(B1))确定一条直线,将f*带入直线方程,用来估计B2的取值.对于j≥2,fmax的取得依靠遗传算法的搜索,随着j的增加算法迭代,每次迭代依赖于Bj-1和Bj来构造下一个缓冲区总容量,直到fmax充分接近目标产出率f*.
当j≥2,Bj由Bj-2和Bj-1决定,可以得出如下方程.
(12)
其中
(13)
(14)
取
(15)
则Bj可表示为
(16)
其中
(17)
(18)
如果BT比较大时,BT与fmax不能保证近似的线性关系,该方法需要进行修正.
3.3 两阶段算法流程
步骤1 设定B0=0,并通过仿真法得出该配置下的fmax(B0),确定初始解B1的值,并初始化遗传算法参数,通过第一阶段遗传算法求解得出fmax(B1),若fmax(B1)≥f*,则输出B1即为最小缓冲区容量,否则令j=2;
步骤2 通过公式(16)计算Bj;
步骤3 通过第一阶段遗传算法获得Bj所对应的fmax(Bj);
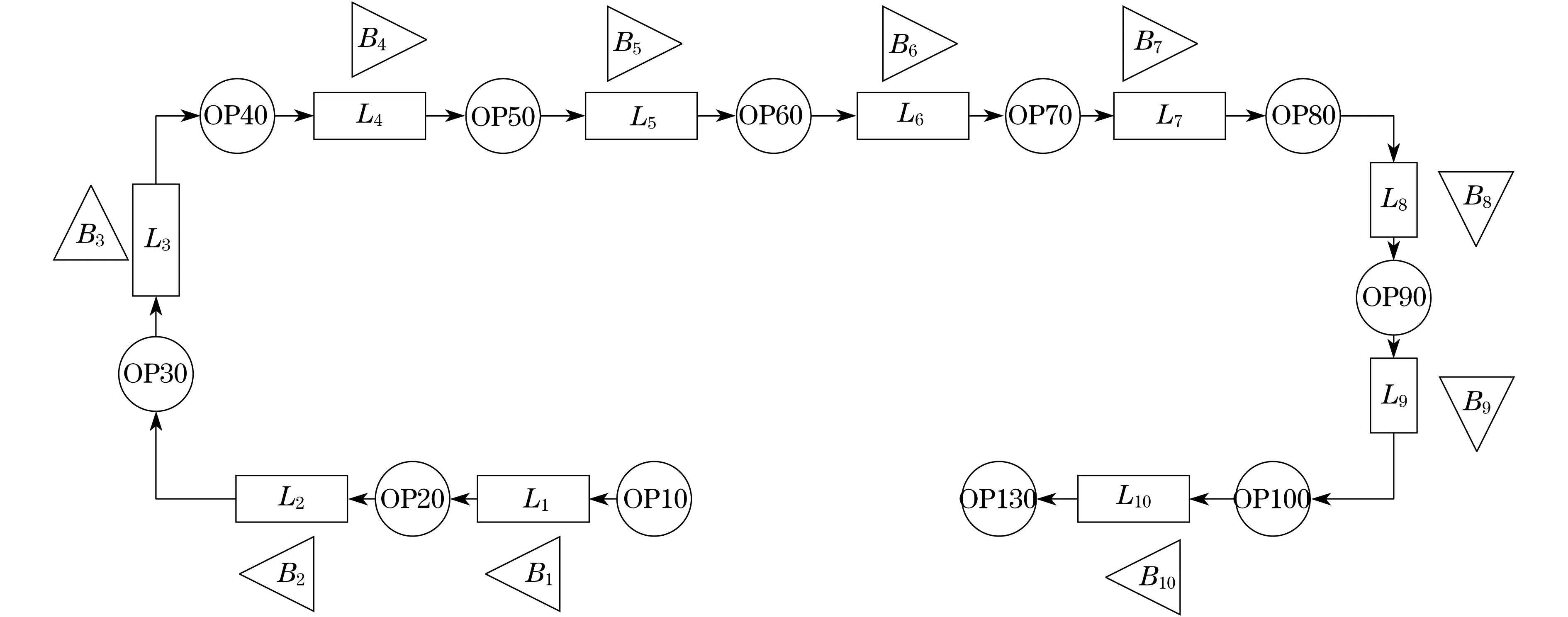
步骤4 对fmax(Bj)进行判断,如果fmax(Bj)≥f*且fmax(Bj-1) 某工厂发动机装配线如AutoCAD图4所示,由发动机总装线(左,只显示内装部分)和缸盖装配支线(右)组成,缸盖装配支线在完成缸盖的装配之后,通过机械手将缸盖运送至总装线与缸体进行合装.总装线要求生产节拍78 s,年产量30万台,每年开工300 d,三班制生产.缸盖装配支线为双排直线环形布置形式,采用动力可积放式辊道输送线,其上配置随行托盘实现装配的柔性流水装配作业,各工位均设有托盘停止器,用于托盘停靠,装配操作为站内操作,即托盘/工件停止于工位内装配,辊道边各工位间均可设置缓冲区. 图4 发动机装配线布局图Fig.4 Layout of the engine assembly line 缸盖装配支线共设置13个工位,配置6个自动站、1个半自动站、1个返修站、4个手动站及1个工件返修出入口;自动站分别完成OP30气门油封压装、OP50止回阀压装、OP70气门锁夹的压装、OP80气门锁夹装配状态检测、OP90气门拍打和OP100气门与油封及座圈密封性检测、缸盖异物排出;半自动站完成OP40气门安装前后的缸盖翻转;返修站完成OP110气门油封、气门及气门锁夹的返修更换;手动站OP10、OP130在缸盖上下线工位设有两台单梁吊车分别完成缸盖的上、下线. 考虑到返修工位的利用率与其他工位相比很小,对整线的物流影响有限,所以没有必要在返修工位前设置额外的缓冲区,因此对该工艺流程稍作简化,去掉返修工位及其相关辊道部分.则缸盖装配支线的工艺流程为:OP10缸盖上线OP20拆卸凸轮轴盖OP30装气门油封OP40装缸盖气门OP50装止回阀OP60装气门弹簧、拧紧火花塞OP70装缸盖气门锁夹OP80激光锁夹检测OP90气门拍打OP100燃烧室密封性检测OP130缸盖下线.根据各工位前后辊道的可用长度,可以确定各辊道可用作缓冲区的容量,如表1所示. 表1 辊道可用作缓冲区的容量 则缸盖装配支线的工位-辊道-缓冲区模型可表示为如图5所示,其中B1至B10表示在工位间辊道旁边所建立的缓冲区. 图5 缸盖装配支线缓冲区模型图Fig.5 Buffer's Model of the cylinder head assembly line 根据所构建的工位-缓冲区-辊道模型,提出发动机缸盖装配支线问题的缓冲区配置模型: (19) (20) (21) 1≤Bi≤10 (22) (23) 其中B′i由表1得出,B′1表示OP10-OP20之间的辊道折算为缓冲区的容量,依次类推,f*表示总装线的产出率,案例以一个月的产出为求解目标,即保证发动机的月产量为f*=33 000,最小化缓冲区的总容量,得出最佳的缓冲区配置方式B=(B′1,B1,...B′10,B10). 按照表2对于缸盖装配支线系统参数进行设置,其中设备故障的发生和修复符合指数分布,故障率表示设备故障发生的数学期望,平均修复时间MTTR表示设备故障修复的数学期望的倒数,各工位的操作时间符合正态分布. 表2 各工位参数设置 按照上述的求解目标设计了相应求解步骤,首先确定B0=0为不设置线边缓冲区,只利用辊道作为缓冲区,进行一次仿真实验得出B0所对应的产出率fmax(B0); 步骤1 令BT=B1=K-1,利用上述遗传算法运算流程获得对应的fmax(B1); 步骤2 利用公式(16)得出B2的值,返给第一阶段的BT; 步骤3 一、二阶段循环迭代,直到fmax(Bj)满足总装线产出率f*,且fmax(Bj-1) 遗传算法运行代数设置为50,变异率0.2 交叉率0.8,每代个体30.将完成一次两阶段的算法实施过程称为一次迭代过程,如图6所示,经过3次迭代之后,获得最小缓冲区容量为23,而且每次迭代所得结果满足线性关系,所以,不需要对算法进行修正,即可得出在满足发动机月产量为33 000(30 d无间断生产)的要求下,缸盖装配支线缓冲区的最小容量为23,相应的最小缓冲区容量配置见表3所示. 图6 两阶段算法迭代图Fig.6 Iteration of two-stage method表3 装配支线最小缓冲区容量配置Tab.3 Optimal buffer allocation of the branch assembly line 辊道辊道容量缓冲区容量辊道辊道容量缓冲区容量OP10-OP2016OP60-OP7001OP20-OP3012OP70-OP8001OP30-OP4031OP80-OP9022OP40-OP5021OP90-OP10020OP50-OP6016OP100-OP13013 分析总装线与装配支线的关系,针对一类异步式装配支线,在线边设置缓冲区,并且利用传送辊道作为缓冲区的补充,建立辊道-缓冲区的装配支线模型,以最小化装配支线缓冲区总容量为优化目标,设计两阶段算法进行求解,第一阶段选择遗传算法求解特定缓冲区总容量下的最大产出率,第二阶段根据Gershwin的研究结果,设计线性迭代算法,案例分析显示在与遗传算法进行结合使用时,能够有效的对第2类缓冲区配置问题进行求解. [1] DEMIR L,TUNALI S,ELIIYI D T.The state of the art on buffer allocation Problem:a comprehensive survey[J].Journal of Intelligent Manufacturing,2014,25(3):371-392. [2] 张良安,梅江平,黄田.基于遗传算法的机器人自动化生产线缓冲区容量分配方法[J].机械工程学报,2010,46(11):101-106. ZHANGLiangan,MEI Jiangping,HUANG Tian.Genetic algorithm-based buffer allocation of a robot production line[J].Journal of Mechanical Engineering,2010,46(11):101-106. [3] 高贵兵,岳文辉,张道兵等.基于马尔可夫过程的混流装配线缓冲区容量研究[J].中国机械工程,2013,24(18):2524-2528. GAO Guibing,YUE Wenhui,ZHANG Daobing et al.Research on buffer capacity for mixed-model assembly lines based on markov Process[J].China Mechanical Engineering,2013,24(18):2524-2528. [4] 宋士刚,李爱平,徐立云.可重组制造系统缓冲区容量的优化研究[J].计算机集成制造系统,2008(10):1951-1956. SONGShigang,LI Aiping,XU Liyun.Buffer capacity optimization in reconfigurable manufacturing system[J].Computer Integrated Manufacturing Systems,2008(10):1951-1956. [5] AMIRI M,MOHTASHAMI A.Buffer allocation in unreliable production lines based on design of experiments,simulation,and genetic algorithm[J].International Journal of Advanced Manufacturing Technology,2012,62(1-4):371-383. [6] THOMAS MCNAMAR,SABRY SHAABAN,SARAH HUDSON.Simulation of unbalanced buffer allocation in unreliable unpaced production lines[J].International Journal of Production Research,2013,51(6):1922-1936. [7] PRZEMYSLAW KORYTKOWSKI,TOMASZ WISNIEWSKI,OLEG ZAIKIN.Optimal buffer allocation in re-entrant job shop production using simulated annealing[J].Management and Production Engineering Review,2010,1(3):30-40. [8] GERSHWIN S B,Schor J E.Efficient algorithms for buffer space allocation[J].Annals of Operations Research,2000,93(4):117-144. [9] 高玮.现代智能仿生算法及其应用[M].北京:科学出版社, 2011. GAO Wei. Modern intelligent algorithm and its application[M].Beijing: Science Press, 2011. [10] MICHALEWICZ Z,FOGEL D B.如何求解问题: 现代启发式方法[M].北京:中国水利水电出版社,2003. MICHALEWICZ Z,FOGEL D B.How to solve it: modern heuristics[M].Beijing:China Water&Power Press,2003. Two-tage solution on buffer allocationfor branch assembly line LI Ai-ping, LI Cong, ZHANG Yan-hong, LIU Xue-mei, XU Li-yun (Institute of Advanced Manufacturing Technology, Tongji University, Shanghai 201804) To solve the material conveyance and buffer allocation problem on branch assembly line, the transfer roller is treated as a complement to buffer. Accordingly, a roller-buffer assembly line model is established for desired production rate with the minimum total buffer capacity. Due thatthe buffer allocation, along with production rate,cannot be expressed by analytical solution, specifically for limited total buffer capacity for stations, a two-stage solution is postulated. In the first stage, the maximum production rate of total buffer capacity is attained using genetic algorithm. In the secondary stage, the branch total buffer capacity, together with buffer allocation optimization,is obtained via Gershwin's theory. To this end, the casesare employed to demonstrate the effectiveness of this approach. branch assembly line;roller;buffer;two-stage solution 上海市科委科技攻关项目(15111105502);上海市重大技术装备研制专项(ZB-ZBYZ-01-14-1562) 李爱平(1951-),女,教授,博士生导师.E-mail:limuzi@tongji.edu.cn TH 181 A 1672-5581(2016)05-0449-064 案例分析




5 结论
