城市化进程中人口变化的动力学分析
2016-08-09叶凯莉王秋燕
叶凯莉,王秋燕 ,宋 强
(1.信阳师范学院 a.工商管理学院;b.数学与信息科学学院, 河南 信阳 464000;2.信阳职业技术学院 数学与计算机科学系, 河南 信阳 464000)
0 引言
伴随着工业化进程的推进和社会经济的发展,城市化现象越来越受到人们的关注.城市化在带动区域经济发展的同时,也引起了城市和农村人口结构的变化.而城市外来人口的增加和农村劳动力的减少对社会也造成了一定的消极影响,因此,控制城市化进程中的人口流动是必要的.
(1)
其中:x,y分别代表城市和乡村人口密度;a,b,c,d为正参数.这里假设x(0)>0,y(0)>0.显而易见,该模型有非平凡平衡点.
本文对系统(1)进行了全局性分析.利用类似于文献[5]的方法,首先给出了解的有界性,然后讨论了平衡点的存在性和稳定性.特别地,对正平衡点的动力学性质进行了系统地研究,得到了其存在性和局部渐近稳定性的条件.然后利用Bendixon-Dulac定理[6]得出了系统不存在非平凡正周期解,进而得到正平衡点是全局渐近稳定的.最后对所得结论进行了讨论和总结.
1 解的有界性
根据解的存在唯一性定理和简单的讨论可知,系统(1)的解总是存在且为正.事实上,由系统(1),易得
这分别意味着

(2)
首先考虑系统(1)中x(t)的有界性.显然,根据解的正性,下面假设c>d.于是,有以下结论:
定理1 对于系统(1),如果c>d,那么
(3)
证明由以上的讨论可知,存在一个T>0,使得当t>T时,y(t)<1.由系统(1)的第二个方程可知,对于t>T,有
于是,得到
这说明,对于c>d,有
通过以上讨论,可以得到下面的结论.
定理2 如果c>d,那么系统(1)是持久的.
2 平衡点分析
2.1 平衡点的存在性
系统(1)有平衡点E0(0,0)和边界平衡点E1(1,0)与E2(0,1).
假设存在正平衡点E*(x*,y*),则有
(4)
结合方程组(4),可得
-(abc+a2d)(x*)2+2ad(a+b)x*+
b2c+abc-a2d-b2d-2abd=0,
(5)

(6)
定义
F(x)=-(abc+a2d)x2+2ad(a+b)x+
b2c+abc-a2d-b2d-2abd,
(7)
(8)
那么(x*,y*)是系统(2)的正平衡点当且仅当x*是F(x)=0的一个正解和y*是正的,其满足方程(8).
注意到方程(5)是一个二次方程,通常来讲,其最多有两个正根.但是,下面将说明多项式(7)仅有一个正根满足式(6).
由式(7)可得,如果Δ=ab2c(a+b)(c-d)≥0,那么方程F(x)=0有正根.
当Δ=0时,F(x)=0只有一个正根x=1,此时y=0,显然这是一个边界平衡点.
当Δ>0即c>d时,F(x)=0有两个正根x1和x2,其中x1>x2>0.由式(8)可得y1>0,y2<0.因此,根据解的正性,仅有一根x*=x1满足式(6),也就是说,E*(x*,y*)是系统(1)唯一的正平衡点.
综上所述,对于系统(1)正平衡点的存在性,有下面的定理.
定理3 如果c≤d,则系统(1)存在一个平衡点E0(0,0)和两个边界平衡点E1(1,0),E2(0,1);不存在正平衡点.如果c>d,则系统(1)存在唯一的正平衡点E*(x*,y*).
2.2 平衡点的稳定性
平衡点E0,E1,E2和E*的稳定性分别是由系统在这些点处的雅克比矩阵J(E0),J(E1),J(E2)和J(E*)的特征值所决定的.易得,系统(2)的雅克比矩阵为
由系统(1)相应的线性系统易得,原点(0,0)处的雅克比矩阵为
显然,无论正平衡点E*是否存在,E0总是一个不稳定的结点.
下面分别将雅克比矩阵J(x,y)的迹和行列式记为A和B.
平衡点(1,0)处的雅克比矩阵J1=J(E1)为
容易看出,它的特征根为λ1=-a和λ2=c-d.当c>d时,即正平衡点存在时,E1是不稳定的,同时,J(E1)的行列式为负,因此,E1是一个鞍点.当c≤d时,正平衡点不存在,此时,A2-4B=(a+c-d)2≥0,且J(E1)的行列式B是非负的,因此E1是一个结点.如果c
平衡点(0,1)处的雅克比矩阵J2=J(E2)为
很明显,它的特征根为λ1=a+b和λ2=-c.因此,E2是一个鞍点.
平衡点(x*,y*)处的雅克比矩阵J*=J(E*)为
J(E*)=
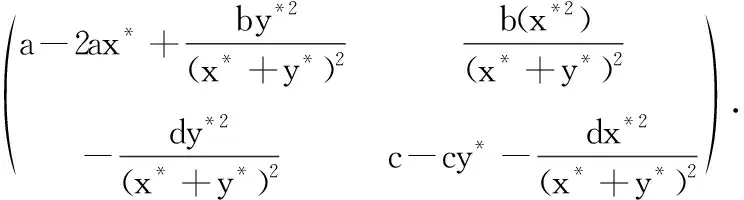
经过简单的计算,可得A<0,B>0,这表明E*是局部渐近稳定的.
综上所述,我们得到下面的定理:
定理4 对于系统(1),无论正平衡点是否存在,总有一个不稳定的结点E0和一个鞍点E2.如果正平衡点存在,即c>d,那么E1是一个鞍点,E*是局部渐近稳定的.如果正平衡点不存在,即c 下面将证明系统不存在非平凡正周期解.显然,要在正平衡点存在的情况下讨论. 若正平衡点外围存在极限环Γ,则Γ必全部位于xOy坐标平面的第一象限内部.下面用Dulac函数法证明这种极限环不可能存在.事实上,在第一象限内取 B(x,y)=xα-1yβ-1, 其中α,β为待定常数.容易算得 xα-1yβ-1((-aα-a)x+(-βc-c)y+ 由于x和y定号,欲使D不变号,只需令 从而可确定α=-1,β=-1.于是, (9) 其中 f(s)=(b-d)s2+2ds-a-b-c, (10) 以上的讨论表明,D不变号等价于f(s)在区间[0,1]上不变号.下面将证明,只要正平衡点存在,就有f(s)≤0,s∈[0,1]. 由式(10)可得,f(0)=-a-b-c<0,f(1)=-a-c+d<0.当b-d≠0时,f(s)曲线顶点的横坐标为 如果b-d>0,那么x0<0,这表明在区间[0,1]上f(s)≤0;如果b-d<0,那么x0>1,这也表明在区间[0,1]上f(s)≤0. 当b-d=0时,以上结论仍然成立. 因此,在正平衡点存在的情况下,式(9)满足f(s)≤0,即总存在一个Dulac函数 因此,根据Bendixson-Dulac定理,可得到以下非平凡正周期解不存在的结论. 定理5 如果系统存在正平衡点,那么它没有非平凡的正周期解. 通过前面的平衡点分析可知,当E*局部渐近稳定时,E0、E1和E2都是不稳定的,同时,系统不存在非平凡正周期解.因此,由定理5可知,所有的正解都趋近于E*,于是,E*是全局渐近稳定的. 定理6 如果c>d,那么E*是全局渐近稳定的. 从上面讨论可以看到,相对于原模型,改进的模型(1)能够表现出更丰富、更合理的动力学行为.原因在于该模型将环境资源因素考虑进来,因而能更准确地体现人口变化规律. 当然,本文并没有进行数值模拟.动力学分析结果表明,该模型在参数的合理范围内并没有表现出复杂的动力学行为.要表现出复杂的行为,它的参数必须突破合理的界限.因此,我们将会在今后的工作中对该模型进行模拟,确定出合理的参数.3 非平凡正周期解的不存在性
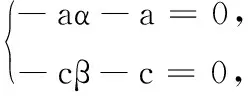

4 讨论

