一力学系统倍频非共振固有振动与阻尼的关系

方天申

(信阳师范学院 物理电子工程学院, 河南 信阳 464000)

0 引言

文献[1-7]讨论了非完全强迫振动系统的非共振固有振动现象.非完全强迫振动系统是指振动媒质不仅受到强迫振动作用，而且能做一定程度的自由振动.大量实验结果表明：当简谐激励的频率fs是系统固有频率fo的n分之一时，即：

(1)

系统可产生非共振固有振动现象.但人们通常把这种非共振固有振动误认为是谐波共振.本文根据实验观测到的一力学系统中，阻尼系数对这种非共振固有振动的振幅和波形的影响，来进一步证明非共振固有振动与谐波共振是在两种不同激励状态条件下的固有振动.

1 实验装置

图1是用两只小型动圈扬声器组成的振动系统，其固有谐振频率f0=218 Hz .其中Y1是振源，由信号源Vs驱动.Y2的纸盆在空气驱动下可产生非完全强迫振动.应用图1示振动系统，可观察研究非共振固有振动与谐波共振的区别.

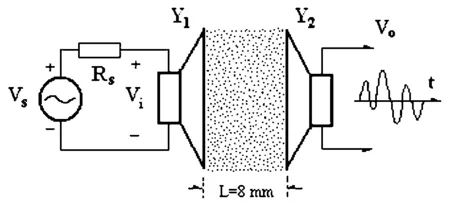
图1 非完全强迫振动实验装置

2 非共振固有振动与阻尼系数δ的关系

阻尼自由振动可归结为二阶微分方程问题：

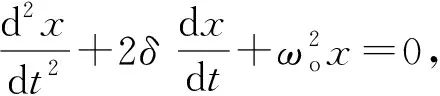
(2)

式(2)中ωo是振动系统的固有频率，δ为阻尼系数.对于图1力学系统：

(3)

在欠阻尼条件下，即力学振动系统的阻力系数γ满足

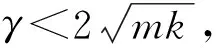
(4)

同时频率满足式(1)条件时，系统才可能产生非共振固有振动.而在过阻尼条件下，则不可能产生非共振固有振动.

3 振幅的周期性变化

对图1振动系统进行实验观察的结果显示：非共振固有振动与谐波共振的区别除了振幅可有很大的差别外，另一重要特征是——谐波共振是等幅振动，而非共振固有振动不是等幅振动.其振幅通常作周期性变化，变化周期即为激励源的周期Ts=1/fs.例如，用图1示实验装置观测扬声器Y2的非共振固有振动曲线波形如图2示.此振动波形，是直接用双踪示波器显示出的扬声器Y2的输出电压波形.然后用摄像头拍下n=2, 3, 4, 5时的图像.其中fs为激励源频率，fo是固有频率.由图2示波形还可看出，Y2振动位移中的强迫振动分量较弱.

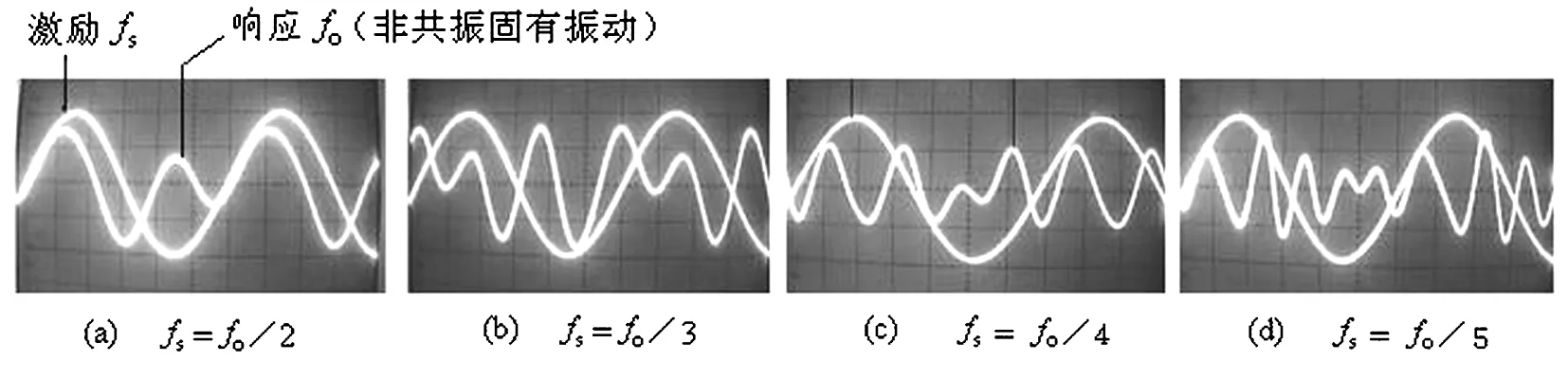
图2 非共振固有振动波形(Y2纸盆不加Δm时) Fig.2 Waveforms of the non-resonant natural vibrations (not adding Δm )

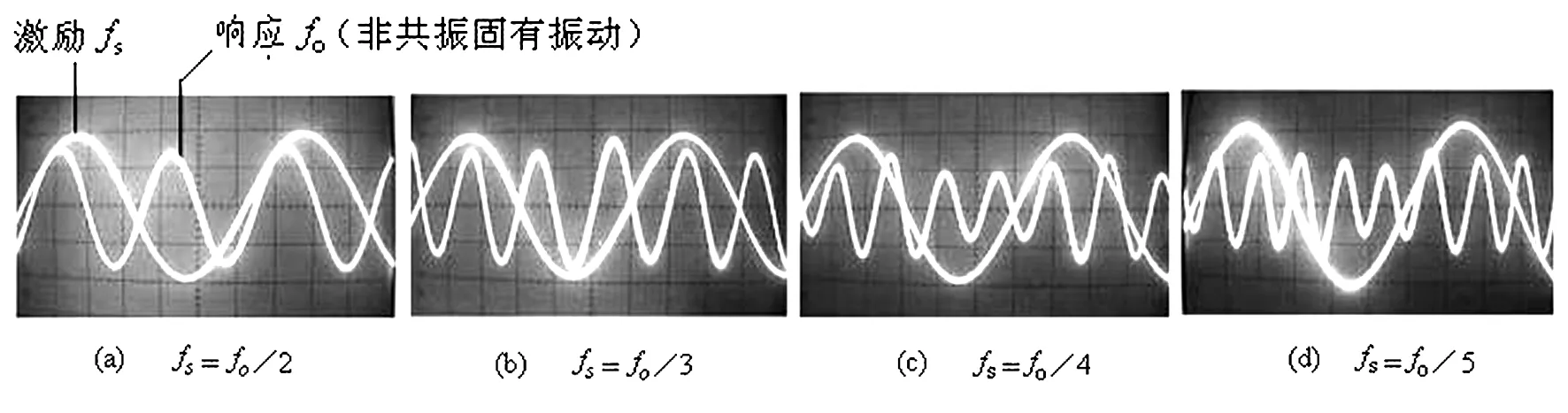
图3 Y2纸盆加有质量m=2.5 g时, 非共振固有振动的波形

4 振动媒质的惯性对固有振动波形的影响

实验研究发现，当改变系统的某一参数时，非共振固有振动的曲线波形会发生变化.例如：在图1实验装置扬声器Y2的纸盆中央，固定一质量Δm=2.5 g的金属圆环(Y1不加Δm)，根据式(3)可知，这会使阻尼系数δ减小.减小程度，可分析计算如下：已知纸盆不加Δm时的固有频率fo1=185 Hz， 加有Δm=2.5 g时的固有频率fo2=136 Hz.根据式(3)，可导出计算纸盆质量的关系式：

(5)

把以上数据代入式(5)可算得纸盆质量m≈2.94 g ；没加Δm时的纸盆质量m0=2.94-2.5=0.44 g.根据式(5)计算可知，加上Δm后，系统阻尼系数减小约6倍.在此条件下实验观测到的非共振固有振动如图3示，与图2相比，其波形产生了显著变化.其实验观测条件是：YD103-4N型扬声器功率为3 W、阻抗为16Ω，激励电压Vi=3 V .

将图3与图2所示波形进行对比可知，系统振动媒体的惯性大小对非共振固有振动的产生和振动状态都有显著影响.

5 结论

文献[1]和本文所描述的固有振动，是非共振固有振动.非共振固有振动与谐波共振都是固有振动.但谐波共振是非简谐激励的谐波分量频率与系统固有频率相同时产生的固有振动.非共振固有振动的激励是简谐量，其频率是固有频率的整数分之一.非共振固有振动只能在一非完全强迫振动系统中才能产生.在完全强迫振动系统中，可产生共振 (或谐波共振) 固有振动，但不能产生非共振固有振动.由于系统振动物理机制不同，因而产生的固有振动具有不同的振动波形.