具有时变传输周期的奇异网络化系统鲁棒控制
2016-08-09王岩岩童艳春李建华
王岩岩,童艳春,刘 伟,*,李建华
(1. 周口师范学院 数学与统计学院, 河南 周口 466001; 2. 华东师范大学 数学系 应用数学与交叉学科研究中心, 上海 200241)
0 引言
过去几十年,奇异系统的研究引起了国内外学者的广泛关注.由于奇异系统自身的特殊性,正常系统的一些结论不能直接推广到奇异系统中,这主要是因为在考虑系统稳定性的同时,还要考虑其正则性和脉冲的消除.到目前为止,对于奇异系统的研究主要针对固定采样周期、时滞及鲁棒稳定性等方面,并取得了一系列的研究成果[1-4].
近年来,随着计算机技术,网络技术的迅猛发展以及控制系统规模的日益扩大,网络化控制系统的研究已进入了一个快速发展的阶段[5-8].在实际工业系统中,奇异网络化控制系统也是广泛存在的.然而,由于奇异系统本身的复杂性,目前对奇异网络化控制系统的研究还比较少[9-10].文献[9]研究了具有有界时滞和控制受限的奇异网络化控制系统的稳定性.文献[10]针对一类正则和无脉冲奇异网络化控制系统,在具有时滞和数据包丢失情况下对系统的稳定性进行了详细的分析.然而,需要指出的是,上述结果都是建立在固定采样周期之上的.
由于网络的引入,采样周期的时变性也是网络化控制中存在的一个基本问题.由于控制策略的不同,采样传输周期在实际网络化控制系统中既可为时不变的,也可为时变的.甚至有时在一些实际控制问题中,时不变周期采样根本就无法实现.然而,到目前为止关于这方面研究还不多见,也不曾出现有效方法.因此,在时变传输周期条件下,对奇异系统网络化控制进行研究很有必要.基于以上分析,本文将根据奇异系统本身的特点,在无传输时延和丢包情况下,将奇异网络化控制系统转化为异步动态系统,利用Lyapunov稳定性理论和线性矩阵不等式方法,对这一问题进行研究.
2 问题描述
本文考虑如图1所示具有时变传输信号的奇异网络化控制系统:
(1)
其中x(t)∈Rn为状态向量,y(t)∈Rr为输出向量;E,A∈Rn×n,B∈Rn×m和C∈Rr×n为常数矩阵,这里E为奇异矩阵,满足rank(E)=q 图1 时变传输周期的广义网络化模型 记hk为采样周期,即hk=tk+1-tk,这里hk为时变的,且存在常数0 本文的目的是获得闭环系统(1)在时变传输周期的条件下二次容许的控制器设计问题.为此,在本文中做出如下假设. 假设:矩阵对(E,A)为正则,无脉冲. 将时变传输周期变量视为参数不确定项,并将其进行离散化.根据假设,矩阵对(E,A)为正则无脉冲,可知存在非奇异矩阵P和Q满足 (2) 将方程(2)离散化,有 (3) 进一步,可得 Z(k+1)= (4) 其中 进一步,有 (5) 其中 且 为方便,记 由于本文工作的需要,我们给出如下引理: 引理1[11]假设G,M和N为具有适当维数的实矩阵,其中G为对称矩阵,那么 G+MFN+NTFTMT<0 对任意满足σmax(F)≤η都成立,当且仅当存在常数ε>0,使得 其中σmax(F)为矩阵F的最大奇异值. 引理2[12]对于具有事件率约束的异步动态系统,考虑如下由连续动力系统离散化后的差分方程 xk+1=fs(xk), 其中s∈{1,2,…,N}.如果存在一个Lyapunov函数V(x)满足 β1‖x‖2≤V(x)≤β2‖x‖2, 其中βi>0,i=1,2,以及标量α1,α2,α3,…,αM>0使得 其中:M为系统的事件个数;r1,r2,…,rM表示事件的发生率;Ms为第s离散状态的事件发生数,则此异步动态系统是指数稳定的. 注1 引理2中具有事件率约束的异步动态系统是指如下元组: Λ=(R+,{1,…,N},Rn,E,R,I,F), 实际上,异步动态系统中比较典型的离散事件是数据包丢失与否.将具有事件约束的连续系统状态如何用离散后的差分方程描述为该定理的主要应用. 本节将给出奇异网络化控制系统在时变传输周期情况下稳定的充分条件.为此,首先给出如下引理. η=(eσmax(A1)hmax-eσmax(A1)hmin)/(σmax(A1)). 证明由2-范数与最大奇异值的关系,可得 (eσmax(A1)hmax-eσmax(A1)hmin)/(σmax(A1)), 从而引理3成立.证毕. 引理4 如果存在对称正定矩阵S∈Rn×n,矩阵X∈Rm×n,以及标量ε>0,α>1使得 (6) 则闭环系统(5)为指数稳定的,此时使得系统稳定的反馈控制增益矩阵可取为 证明对于式(6),根据Schur补引理可知, 进一步, 利用引理1和引理3可得, 即有 (7) 定义Lyapunov函数 V(Z(k))=ZT(k)PZ(k), 其差分描述为如下形式: V(Z(k+1))-α-2V(Z(k))= ZT(k+1)PZ(k+1)-ZT(k)PZ(k)= ZT(k)ΩZ(k), V(Z(k+1))-α-2V(Z(k))<0. 因此引理4成立,证毕. 根据引理4,下面给出奇异网络化控制系统(1)在时变传输周期情况下可稳的充分条件. 定理1 如果存在对称正定矩阵S∈Rn×n,矩阵X∈Rm×n,以及标量ε>0,α>1使得如下线性矩阵不等式成立 (8) 其中 则闭环系统(1)在时变传输周期hk∈[hmin,hmax]下是指数稳定的,此外控制增益矩阵可取为K=XS-1Q-1. 证明对于由式(1)所描述的奇异网络化控制系统,假若数据包失率为r1=0,则根据引理2可知方程(5)可用来描述连续动力系统(1)离散化后的差分方程,从而利用引理4即可获得定理1成立.证毕. 为了说明本文所提出方法的有效性.考虑奇异网络化控制系统(1),其参数给出如下 通过验证可知,此系统为正则和无脉冲的,因此存在非奇异矩阵 满足 如果取hmin=0.1,hmax=0.4,α=1.151>1,那么 利用Matlab工具箱求解式(8),得到如下参数 ε=1.020 9. 进一步可获得反馈控制增益矩阵为 K=XS-1Q-1=(-0.668 0 0.000 7). 图2 闭环系统的状态响应 本文研究了对于存在有界时变传输周期的奇异网络化控制系统的稳定性问题.在无传输时延和数据包丢失的情况下,将其转化为异步动态不确定系统.利用Lyapunov稳定性理论和线性矩阵不等式的方法给出了系统指数稳定的充分条件,同时获得了系统指数稳定的状态反馈控制律.最后通过仿真算例验证了本文方法的有效性.在本文中,没有考虑量化的影响,如果同时考虑量化误差对系统控制的影响,相应的研究会变得更加复杂.这些都是需要进一步研究的问题.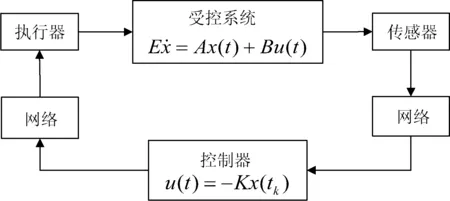
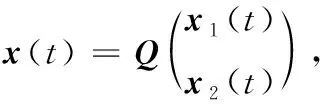




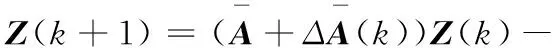





3 主要结果
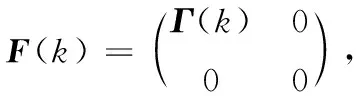

4 仿真例子
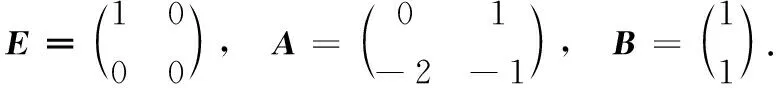




5 结论
