两级定轴齿轮断齿故障的非线性耦合特性研究

王　鑫， 徐玉秀， 武宝林， 李涛涛

(1.天津工业大学 机械工程学院,天津　300387； 2.现代机电装备技术重点实验室,天津　300387；3.三一重型能源装备有限公司,北京　102206)

两级定轴齿轮断齿故障的非线性耦合特性研究

王鑫1,2， 徐玉秀1,2， 武宝林1， 李涛涛3

(1.天津工业大学 机械工程学院,天津300387； 2.现代机电装备技术重点实验室,天津300387；3.三一重型能源装备有限公司,北京102206)

为研究两级齿轮传动系统断齿故障的非线性耦合特性，建立了包含时变啮合刚度、齿侧间隙和综合啮合误差等非线性因素的单级及两级齿轮量纲一动力学方程。利用数值方法对建立的非线性微分方程进行求解，获得系统的分岔图、相图及Poincaré截面，对比研究两系统中一级齿轮随激励频率变化的分岔特性及断齿故障下的故障特性。研究结果表明：耦合特性使两级齿轮系统的周期运动区间增加，幅值亦增加，混沌区间缩短并延迟，对混沌起到抑制作用；断齿故障使单级齿轮系统突跳点增加，同时阵发周期运动出现变化，且变化趋势不确定，对于两级齿轮系统仅使阵发周期运动幅值增加。

齿轮传动；非线性耦合动力学；混沌；分岔；故障

齿侧间隙可使齿轮系统的动力学行为成为非线性状态。对于含两个齿侧间隙的两级齿轮系统的动力学状态将产生非线性耦合，会使系统的混沌运动状态发生改变[1-2]。当上述系统有故障时，就会引起故障激励与齿侧间隙的非线性状态的复杂耦合，使系统的复杂动力学状态难以确定，对此故障也难以识别。只有准确建立多间隙的非线性耦合模型、故障与多间隙的非线性耦合模型，分析出各耦合关系和影响特性，才能找出齿轮系统在故障状态下的非线性耦合特性，把握故障对耦合特性的影响。

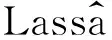
对于齿轮故障特性的研究，马锐等[5-7]分析了含齿侧间隙的单级齿轮分别在断齿故障、裂纹故障及局部剥落故障情况下的非线性动力学特性。王彦刚等[8-9]研究了含齿侧间隙的单级齿轮分别在单齿冲击、单齿刚度(断齿故障)、单齿及全齿磨损故障状态下的分岔特性，提出可以通过齿轮振子检测齿轮断齿程度。Wang等[10]发现，齿面摩擦会使含间隙单级齿轮系统的倍周期分岔、准周期分岔及混沌运动发生延迟。

上述文献主要研究含间隙单级齿轮系统的故障特性及间隙、负载等参数对耦合系统的影响，没有进行故障与多间隙的非线性耦合研究。本文从非线性动力学角度，分别建立考虑时变啮合刚度、齿侧间隙和综合啮合误差等非线性因素的单级及两级定轴齿轮传动系统的量纲一动力学方程，对比两个系统的分岔特性及耦合特性，分别分析断齿故障对两个系统的耦合非线性影响，找到非线性系统的故障特性，以便进行有效的故障识别。

1　两级定轴齿轮系统扭转动力学模型

图1为两级定轴齿轮减速器系统扭转动力学模型，所有齿轮均为直齿圆柱齿轮。该模型不考虑各齿轮之间的横向振动位移，并假设系统各构件为刚体，齿轮啮合参数用弹簧和阻尼器进行模拟，忽略齿面啮合摩擦力的影响。当系统仅有齿轮1，2时为单级齿轮动力学模型。

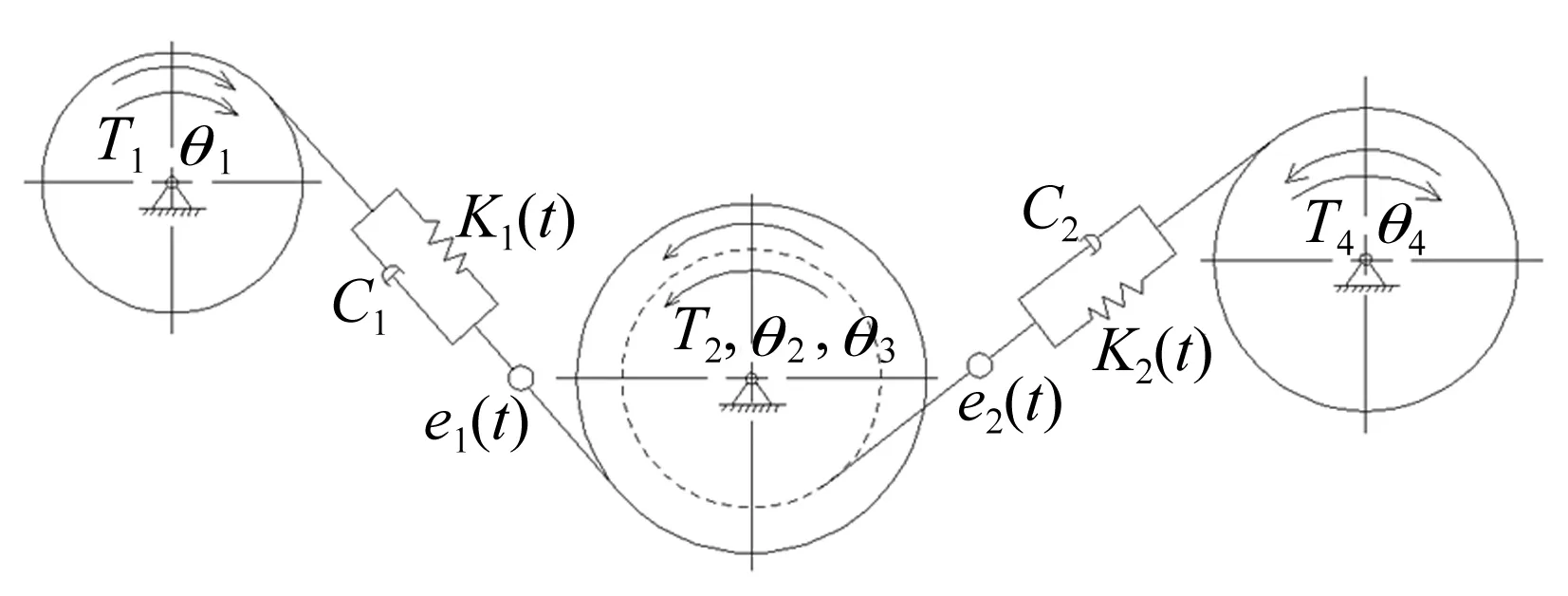
图1　两级定轴齿轮扭转动力学模型Fig.1 Torsional dynamic model of two-stage gear

图1中θi(i=1，2，3，4)为各齿轮的扭转位移，C1、C2、K1(t)、K2(t)为齿轮啮合副的等效阻尼和时变啮合刚度，e1(t)、e2(t)为齿轮副综合啮合误差，T1、T4为输入扭矩、负载扭矩。

2　系统的运动微分方程

2.1两级齿轮运动微分方程

在考虑齿侧间隙、时变啮合刚度、综合啮合误差的基础上，根据拉格朗日方程建立图1所示系统的运动微分方程：

(1)

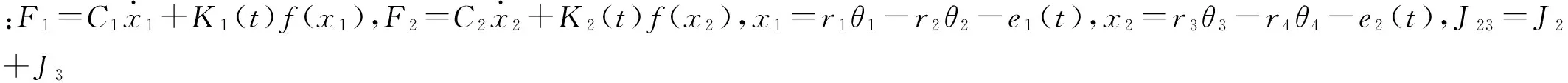
Ji(i=1，2，3，4)为轴上各齿轮的转动惯量；ri(i=1，2，3，4)为各齿轮的基圆半径；

f(xi)(i=1，2)为齿侧间隙非线性函数，定义为：

(2)

式中：bi(i=1，2)为齿侧间隙的一半。

在不考虑齿轮传动效率的情况下，系统力矩平衡时齿轮的静态啮合力为

(3)

则负载扭矩与输入扭矩的关系为

(4)

齿轮副的时变啮合刚度Ki(t)可表示为

Ki(t)=Kmi+Kaisin(wmit+φi)

(5)

式中：Kmi为第i级齿轮副平均啮合刚度，Kai为第i级齿轮副啮合刚度变化幅值，wmi为第i级齿轮副啮合频率，φi为第i级齿轮副啮合刚度变化幅值的初始相位。

阻尼系数表达式为

(6)

式中：ξ1、ξ2分别为一、二级齿轮副的阻尼比；mi(i=1，2，3)为第i个齿轮的质量。

齿轮副的综合啮合误差采用啮合函数的一次谐波形式，即

ei(t)=eaisin(wmit+φi)

(7)

对方程(1)化简，得

(8)

式中：me1、me2、me3为齿轮的等效质量，且

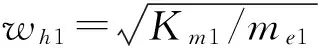
对方程(8)进行归一化处理，得系统量纲一运动微分方程组：

(9)

式中：Ωi=wmi/wh1，i=1，2为量纲一激励频率；

量纲一时变啮合刚度为

Ki(τ)=1+εisin(Ωiτ+φi)

(10)

其中εi=Kai/Kmi，i=1，2。

2.2单级齿轮运动微分方程

回屋的路上，大梁说，我把事情原原本本都跟慢成讲了，他说二丫看到的那个东洋人，应该可以肯定是狼剩儿。他们查到，从二十一年开始，东洋人就假装看风水、货郎担，到湖北来找矿。除了铁冶，大冶、阳新、荆门、宜昌，都有。东洋人顺带拐走狼剩儿，养大了又让他当兵，这完全有可能。

单级齿轮运动微分方程为第一级齿轮运动微分方程，其推导公式与两级齿轮相同，量纲一运动微分方程为

(11)

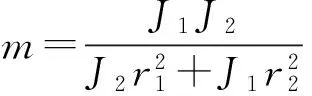
2.3刚度故障函数的建立准则

当齿轮存在单齿局部断齿故障(如图2所示，单齿齿宽减少40%)时，在其断齿处刚度会减弱，而其他齿处刚度不变。依据GB/T3480-1997渐开线圆柱齿轮承载能力计算方法中平均啮合刚度的计算公式[11]

Kmi=Crh

(12)

式中Cr是端面内轮齿总刚度的平均值，h为齿宽，取Cr=20 N/(mm·μm)，h=15 mm。

图2　定轴齿轮断齿故障Fig.2 Spur gear with chipping fault

由式(12)可知，齿宽与平均啮合刚度成正比。单齿发生断齿故障时，其齿宽变小，导致单齿平均啮合刚度变小。式(10)中正常状态下量纲一平均啮合刚度为1，故用aδ(τ)表示断齿故障。δ(τ)为幅值为1的周期脉冲函数，周期为齿轮旋转一周的时间，脉冲宽比为1∶N(N为齿轮齿数)；a为断齿程度，由于受到刚度波动影响，取值范围[0，0.8)， 图2所示故障取a=0.4。将故障函数添加到式(10)，即得到量纲一时变啮合刚度故障函数[8,12]

Ki(τ)=1+εisin(Ωiτ+φi)-aδ(τ)

(13)

3　非线性系统耦合特性分析

3.1单级与两级齿轮耦合特性分析

为研究两级齿轮系统的耦合特性，将其与单级齿轮的非线性特性进行对比，考察第二级齿轮对第一级齿轮分岔及混沌特性的影响。分别计算图1所示单级及两级齿轮的非线性动力学响应。其中两级定轴齿轮传动系统的结构参数如表1、2，压力角α=20°，T1=6.5 N·m。表2中的取值在两对齿轮的啮合线上相等，故省略下标i。

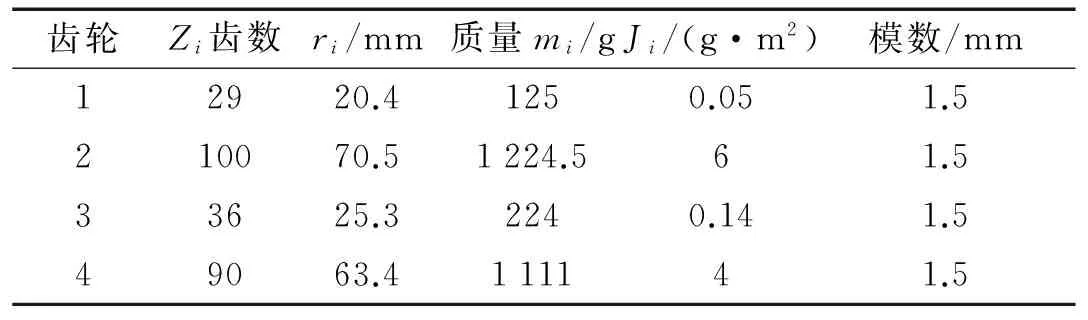
表1　各齿轮的参数

表2　计算参数

采用变步长Runge-Kutta法对非线性微分方程组(9)、(11)进行数值求解，对比正常情况下单级齿轮及两级齿轮系统中第一级齿轮的位移分岔图，观察第二级齿轮对第一级齿轮的影响。

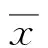
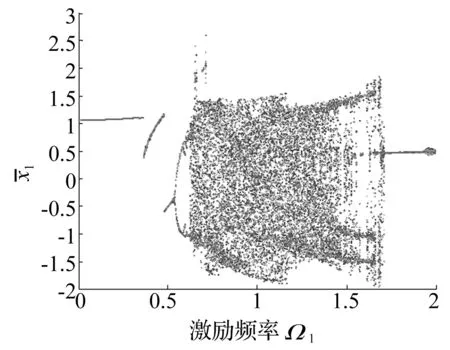
图3　单级齿轮位移分岔图Fig.3 Displacement bifurcation diagram ofthe single gear pair

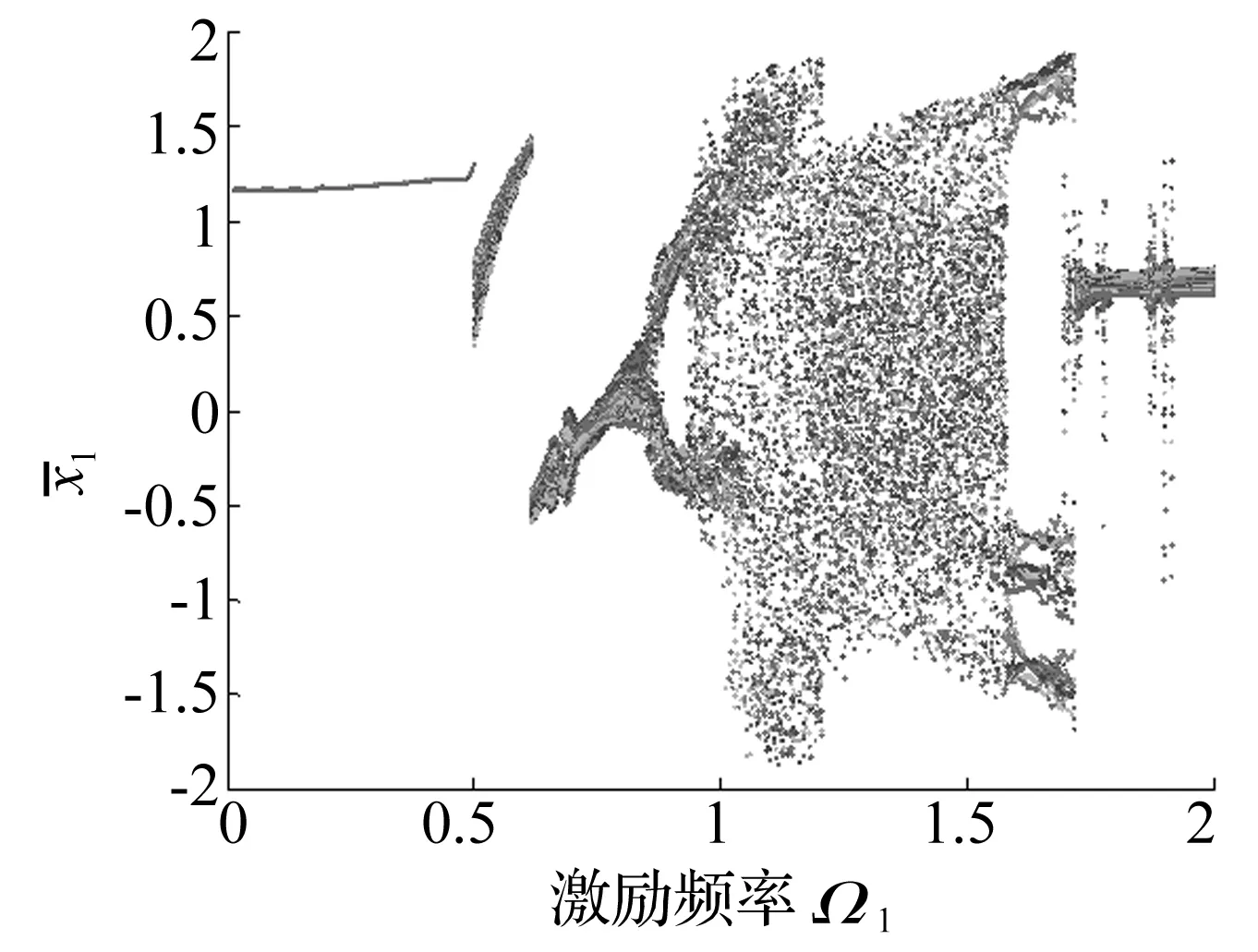
图4　两级齿轮系统中第一级齿轮位移分岔图Fig.4 Displacement bifurcation diagram of the first gear in two-stage gear

上述分析可见，相比于单级齿轮系统，两级齿轮系统周期运动区间增加且幅值增加；混沌区间缩短并延迟，阵发周期运动受到抑制，失稳减少。

对于两级齿轮系统，由于一级齿轮信号中含有二级齿轮的振动特性，使得周期运动幅值增加；当一对齿轮发生脱齿，另一对齿轮处于接触状态时，耦合特性减少了混沌齿轮出现的脱齿碰撞现象，进而减少并延迟了混沌运动，起到抑制混沌的作用。

3.2断齿故障特性分析

设第一级齿轮有断齿故障，将故障激励函数式(13)分别代入式(9)的一级齿轮及式(11)中，计算其分岔图。经计算发现，单级齿轮及两级齿轮在故障状态下的分岔图(图5，6)分别与无故障(图3，4)时基本一致。

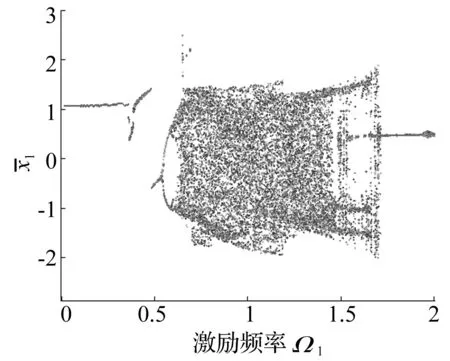
图5　单级齿轮故障状态下分岔图Fig.5 Displacement bifurcation diagram of the single gear pair under chipping fault

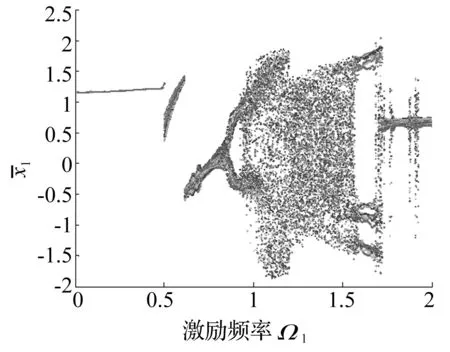
图6　两级齿轮系统中第一级齿轮故障状态下位移分岔图Fig.6 Displacement bifurcation diagram of the first gear in two-stage gear under chipping fault

由图5和图3比较可见，单级齿轮在激励频率较低时Ω1=0.2～0.3时，由于故障的增加，平稳的周期运动变成波动形式，这种波动在Ω1=0.38处变成突跳，增加了突跳点，之后进入平稳周期运动。其分岔点与混沌区间不变，阵发周期运动区间的混沌运动有所减少。

由图6和图4比较可见，两级齿轮系统在激励频率较低时没有出现波动，因此没有增加突跳点，在阵发周期运动Ω1=1.7及1.874处幅值增加。对此，需要对两系统出现变化的各激励频率位置进行研究。

3.2.1单级齿轮正常与故障特性对比

单级齿轮系统在Ω1=0.38时随断齿程度a变化的位移分岔图如图7(a)所示。正常状态下其运动状态为周期运动，当a=0.4时出现跳跃，之后在a=0.6时变为混沌运动，最终回归周期运动。正常状态下(即a=0时)系统相图及Poincaré截面如图7(b)，此时相图为一锥形圆环，Poincaré截面为一个点。随断齿程度增加，当a=0.7时，系统处于混沌运动，如图7(c)，锥形圆环环带变宽且不重合，Poincaré截面分散呈不规则状。

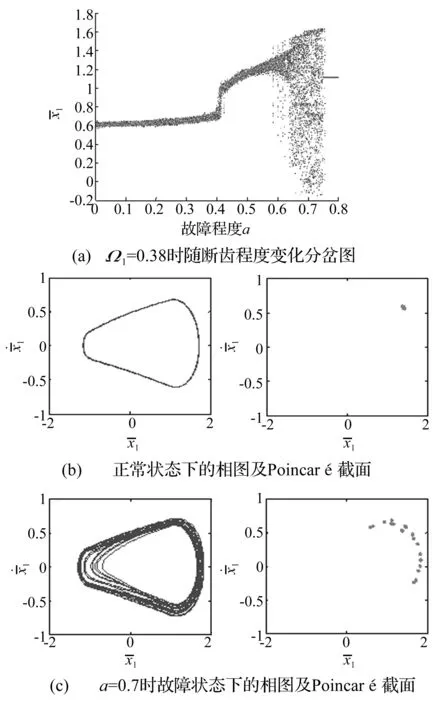
图7　Ω1=0.38时正常与故障状态下单级齿轮系统相图Poincaré截面Fig.7 System phase contrail and Poincaré section of the single gear pair in states of normal and stiffness fault at Ω1=0.38

由图5可知，发生故障时阵发周期运动区间的混沌运动出现变化，在此取两个阵发周期运动中的临近激励频率Ω1=1.466、Ω1=1.47做分岔分析。当Ω1=1.466时，系统随断齿程度a的位移分岔图如图8(a)所示。正常状态下为混沌运动如图8(b)，Poincaré截面为无规则点团；随故障增加，由混沌运动变为3周期运动，如图8(c)， Poincaré截面为3点团；故障继续增加，系统又变为混沌运动，如图8(d)，Poincaré截面为不规则点团。与其相邻的激励频率Ω1=1.47则表现出不同的运动状态变化。随故障增加由3周期运动变为阵发周期运动再变为3周期运动，如图9所示。在如此临近的两激励频率下，各自的运动状态变化却出现了不同，这是由于阵发周期运动本就变化不定，故障的增加使得每一激励频率的变化趋势都变得不确定。

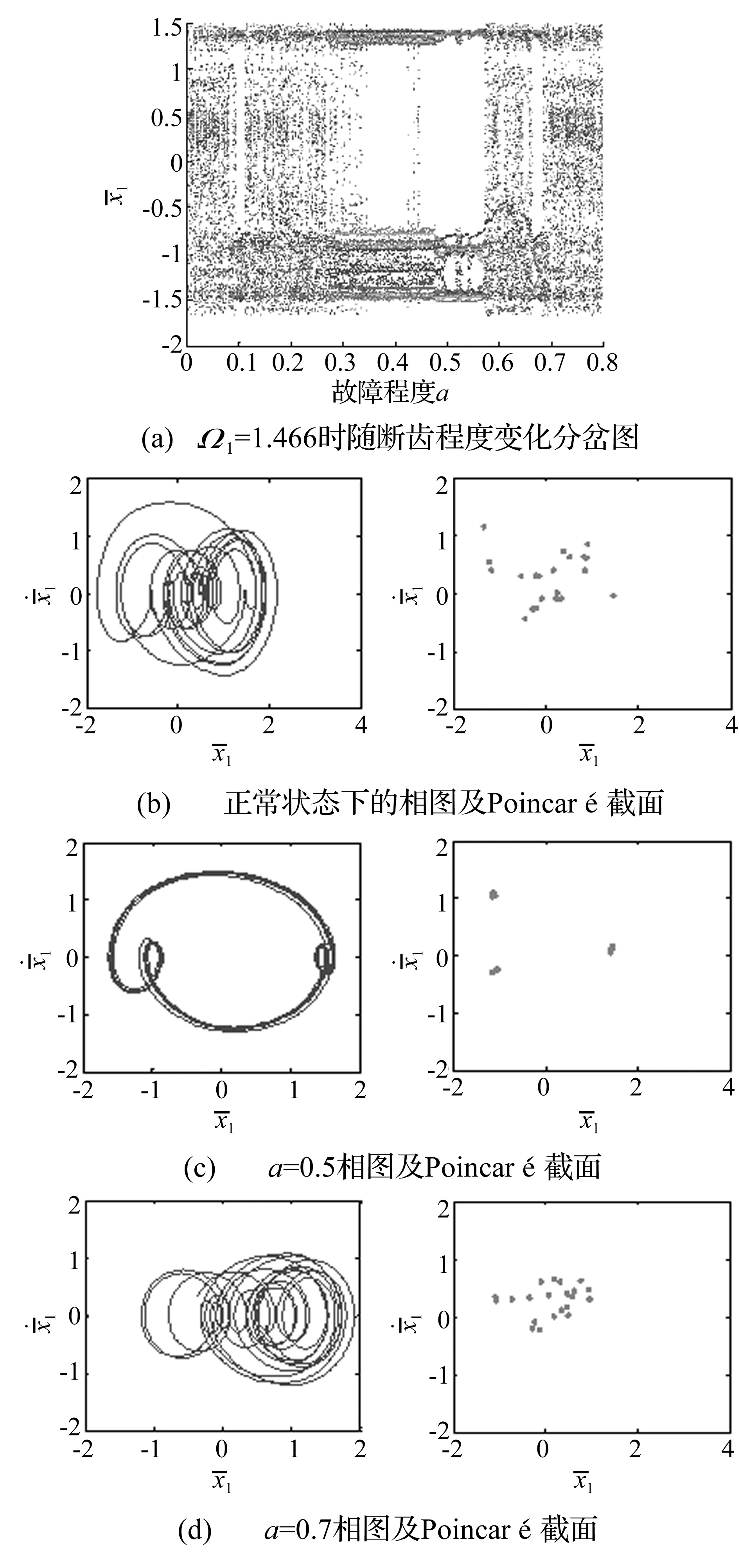
图8　Ω1=1.466时正常与故障状态下单级齿轮系统分岔图、相图及Poincaré截面Fig.8 System bifurcation diagram, phase contrail and Poincaré section of the single gear pair in states of normal and stiffness fault at Ω1=1.466

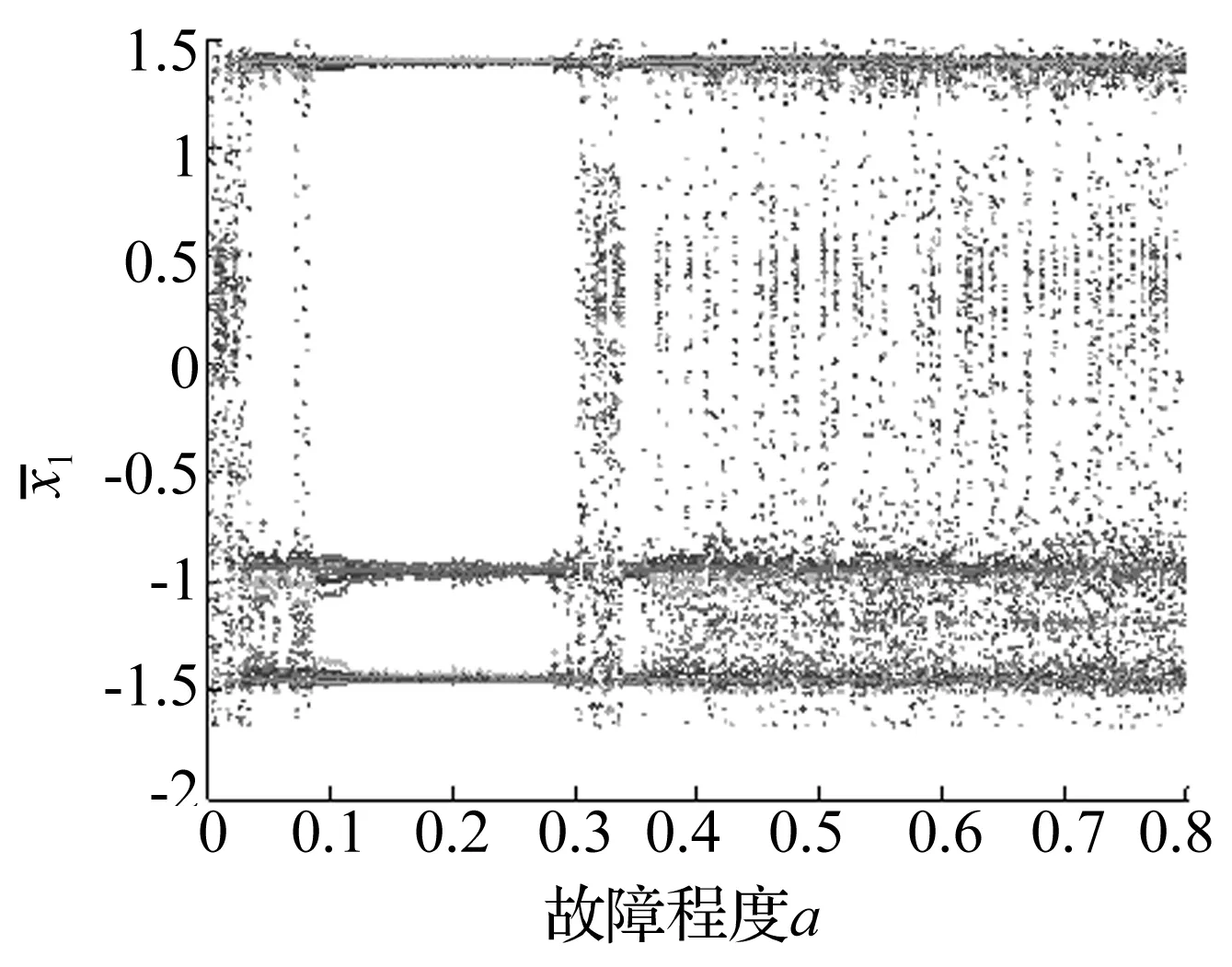
图9　Ω1=1.47时正常与故障状态下单级齿轮系统分岔图、相图及Poincaré截面Fig.9 System bifurcation diagram, phase contrail and Poincaré section of the single gear pair in states of normal and stiffness fault at Ω1=1.47

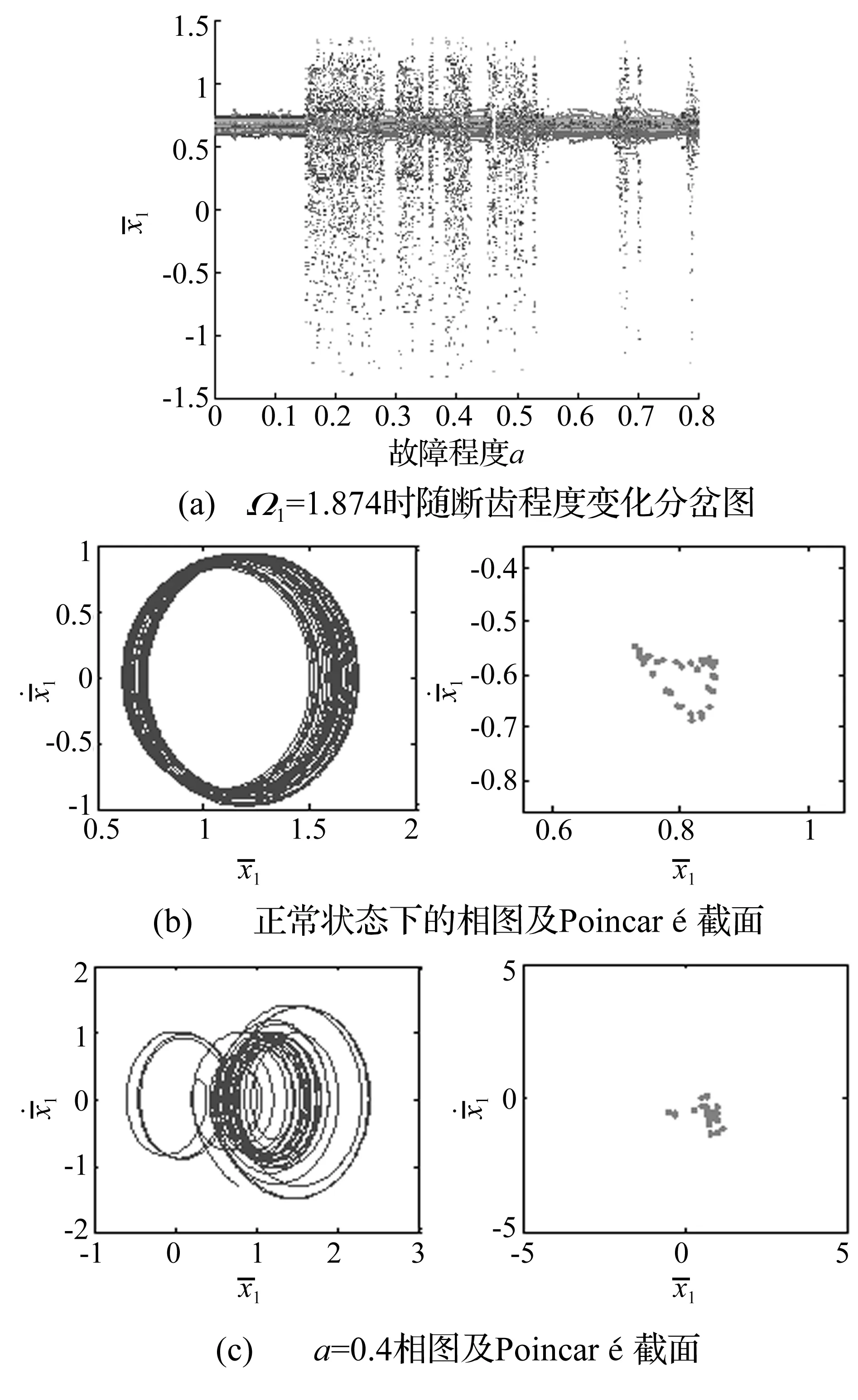
图10　Ω1=1.874时正常与故障状态下两级齿轮系统中一级齿轮的分岔图、相图及Poincaré截面Fig.10 System bifurcation diagram, phase contrail and Poincaré section of the first gear in two-stage gear in states of normal and stiffness fault at Ω1=1.874

3.2.2两级齿轮系统正常与故障特性对比

由3.2中的图6可知，两级齿轮系统发生断齿故障时，在Ω1=1.7及1.874这两处的变化规律相同，在此仅给出两级齿轮系统中一级齿轮在Ω1=1.874时的位移分岔图，如图10(a)。正常状态下系统处于拟周期运动，如图10(b)，相图为圆形环带，Poincaré截面为封闭环；当故障增加时，系统出现阵发周期运动，如a=0.4时系统为混沌运动，如图10(c)，此时相图为不规则曲线，Poincaré截面呈不规则点团。与单级齿轮相比，两级齿轮系统受故障影响较小，这是由于耦合特性抑制混沌的同时也抑制了故障特性。

4　结　论

(1) 对于两级齿轮系统，由于一级齿轮信号中含有二级齿轮的振动特征，使其周期运动幅值增加。

(2) 耦合特性使两级齿轮系统的周期运动区间增加，混沌区间缩短并延迟，阵发周期运动被抑制，失稳减少。

(3) 断齿故障使单级齿轮系统激励频率较低时变得不稳定，增加了突跳点，阵发周期运动出现变化，且变化趋势不确定。而对于两级齿轮系统由于耦合特性的抑制作用，断齿故障仅使阵发周期运动幅值增加。

[1] 林腾蛟，王丹华，冉雄涛，等. 多级齿轮传动系统耦合非线性振动特性分析[J]. 振动与冲击，2013, 32(17): 1-7.

LIN Teng-jiao, WANG Dan-hua, RAN Xiong-tao, et al. Coupled nonlinear vibration analysis of a multi-stage gear transmission system [J]. Journal of Vibration and Shock, 2013, 32(16): 37-43.

[2] 李晟，吴庆鸣，张志强，等. 两级行星轮系分岔与混沌特性研究[J]. 中国机械工程，2014, 25(7): 931-937.

LI Sheng, WU Qing-ming, ZHANG Zhi-qiang, et al. Bifurcation and chaos characteristics of two-stage planetary gear train sets [J]. China Mechanical Engineering, 2014, 25(7): 931-937.

[3] 朱才朝, 黄泽好, 唐倩, 等. 风力发电齿轮箱系统耦合非线性动态特性的研究[J]. 机械工程学报, 2005, 41(8): 203-207.

ZHU Cai-chao, HUANG Ze-hao, TANG Qian, et al. Analysis of nonlinear coupling dynamic characteristic of gearbox system about wind-driven generator [J]. Journal of Mechanical Engineering, 2005, 41(8): 203-207.

[5] 马锐, 陈予恕. 齿轮传动系统断齿故障的机理研究[J]. 振动与冲击, 2013, 32(21): 47-51.

MA Rui, CHEN Yu-shu. Fault mechanism of a gear system with tooth broken[J]. Journal of Vibration and Shock, 2013, 32(21): 47-51.

[6] 马锐，陈予恕. 含裂纹故障齿轮系统的非线性动力学研究[J]. 机械工程学报，2011, 47(21): 84-90.

MA Rui, CHEN Yu-shu. Nonlinear dynamic research on gear system with cracked failure [J]. Journal of Mechanical Engineering, 2011, 47(21): 84-90.

[7] Ma R, Chen Y S, Cao Q J. Research on dynamics and fault mechanism of spur gear pair with spalling defect [J]. Journal of Sound and Vibration, 2012, 331: 2097-2109.

[8] 王彦刚，郑海起，杨通强，等. 故障参数下齿轮系统非线性动力学行为[J]. 振动、测试与诊断，2011, 31(5): 570-574.

WANG Yan-gang, ZHENG Hai-qi, YANG Tong-qiang, et al. Nonlinear dynamics behavior of gear system with fault parameters [J]. Journal of Vibration, Measurement & Diagnosis, 2011, 31(5): 570-574.

[9] 王彦刚，郑海起，杨通强,等. 非线性齿轮系统单齿故障动力学特性[J]. 振动、测试与诊断，2010, 30(6): 654-656.

WANG Yan-gang, ZHENG Hai-qi, YANG Tong-qiang, et al. Non-linear dynamic characteristics of gear system with single-tooth fault [J]. Journal of Vibration, Measurement & Diagnosis, 2010, 30(6): 654-656.

[10] Wang J, Zheng J H, Yang A B. An analytical study of bifurcation and chaos in a spur gear pair with sliding friction [J]. Procedia Engineering, 2012, 31: 563-570.

[11] 秦大同, 邢子坤, 王建宏. 基于动力学和可靠性的风力发电齿轮传动系统参数优化设计[J]. 机械工程学报, 2008, 44(7): 24-31.

QIN Da-tong, XING Zi-kun, WANG Jian-hong. Optimization design of system parameters of the gear transmission of wind turbine based on dynamics and reliability [J]. Journal of Mechanical Engineering, 2008, 44(7):24-31.

[12] 申永军, 杨绍普. 齿轮系统的非线性动力学与故障诊断[M]. 北京: 科学出版社, 2014.

Coupled nonlinear characteristic of a two-stage gear system with chipping fault

WANG Xin1,2, XU Yu-xiu1,2, WU Bao-lin1, LI Tao-tao3

(1. School of Mechanical Engineering, Tianjin Polytechnic University, Tianjin 300387, China;2. Key Laboratory of Advanced Mechatronics Equipment Technology, Tianjin 300387, China;3. Sany Heavy Energy Machinery Co., Ltd, Beijing 102206, China)

In order to investigate the coupled nonlinear characteristic of a two-stage gear system with chipping fault, nonlinear dynamic dimensionless equations of a single gear pair and a two-stage gear system with time varying meshing stiffness, errors of transmission and backlashes were established and solved with the numerical method. The bifurcation and chipping fault properties of the 1st gear pair in both systems were analyzed by using bifurcation diagram, phase contrail and Poincaré section with increase in excitation frequency. The results showed that the two-stage gear system periodic motion interval and its amplitude increase and its chaotic interval shortens and delays due to coupling characteristics, they have a suppressing effect on chaos; the tooth chipping failure makes increase in critical points and changes intermittent periodic movements into uncertain ones for the single stage gear system, and makes increase in intermittent periodic motion amplitude for the two-stage gear system.

gear transmission; nonlinearly coupled dynamics; chaos; bifurcation; fault

10.13465/j.cnki.jvs.2016.13.020

国家重大科技成果转化项目(2060403)；天津市自然科学基金项目(10JCZDJC23400;13JCQNJC07000)

2015-04-09修改稿收到日期：2015-07-17

王鑫 女，博士生，1985年5月生

武宝林 男，教授，博士生导师，1962年10月生

TH132.41

A