法拉第效应对N掺杂硅耦合腔光波导群速度的调控研究

孙海竹， 张建心,韩锴，黄宝歆

(潍坊学院物理与光电工程学院，山东 潍坊 261061)



法拉第效应对N掺杂硅耦合腔光波导群速度的调控研究

孙海竹， 张建心*,韩锴，黄宝歆

(潍坊学院物理与光电工程学院，山东 潍坊 261061)

摘要：耦合腔光波导是由光子晶体点缺陷的缺陷模式相互耦合而实现的，群速度是其重要的性能指标。本文模拟了由N掺杂半导体硅构成的光子晶体耦合腔光波导的能带结构。模拟发现，借助N掺杂半导体硅的法拉第效应，逆着光的传播方向施加磁场，缺陷模式所对应的相对介电参数会变小，群速度也随之逐渐降低，可以获得2.088×10-4c的群速度，证实了法拉第磁光效应对波导群速度的调控作用。这一性能为如何在太赫兹或更低频段实现慢光效应提供了一种新的有效方式。

关键词：光子晶体；耦合腔光波导；群速度；太赫兹频段

1引 言

光子晶体作为一种新型的人工材料受到广泛的关注，一个主要的原因就是其存在带隙[1-2]。带隙的存在使得人们可以调控电磁场的传播，为光调制器[3]、光开关[4]和可调谐的共振腔[5]的设计提供了可能。光子晶体的调谐性能依赖于其中至少一种构成材料的电容率和磁导率的可调制性能。材料的电容率和磁导率的调制可以通过施加静电场[6]、温度[7]、流体静压力[8]和外加磁场[9]等外加参量来实现。由于法拉第磁光效应，磁场对于色散介质的介电参数具有较强的调控作用，因此磁场调制光子晶体的带隙的速度可以更快也更容易。目前为止，人们的研究主要集中其利用垂直方向施加磁场来调制光子晶体的带隙并用来设计器件[10-14]，对于基于法拉第效应的N掺杂半导体硅光子晶体及其器件的研究比较少。Aly等[15]研究了N掺杂半导体硅光子晶体能带的可调谐性，证明外加磁场可以强烈地调制N掺杂半导体硅光子晶体的能带结构，但并没有利用这一性能设计相关光子晶体器件的报道。

太赫兹频段包含了大量的物理和化学信息，在星际观测、国土安全以及医疗诊断等方面都有巨大的应用价值。在此背景下，人们一直致力于实现高效率、低成本、室温下工作的太赫兹源和探测器[16]。如果能够在太赫兹频段实现慢光效应，将为常温下太赫兹波的直接探测提供新的思路和方法。耦合腔光波导作为一种很重要的慢光器件，被广泛应用于光波传输、限制自发辐射等领域[17]。耦合腔光波导的光传输是通过相邻缺陷腔模式之间的耦合来实现的。通过减弱相邻微腔的耦合强度可以很容易地实现慢光效应。本文计算了二维正方晶格N掺杂硅光子晶体点缺陷和由点缺陷构成的耦合腔光波导的能带结构。模拟发现，在逆着光的传播方向施加磁场，缺陷频率所对应的相对介电参数变小，可以获得较小的群速度，这为如何在太赫兹或更低频段实现慢光效应提供了一种新的有效方式。

2理论模拟和结果分析

基于法拉第效应，N型半导体硅的相对介电参数为[15]：

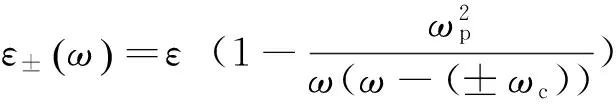
(1)

其中相对介电参数ε的下标正号表示右旋圆偏振，即顺着光的传播方向加外磁场,负号表示左旋圆偏振，即逆着光的传播方向加外磁场。公式中的ε∞=11.7，ωc=eB/m*为回旋频率，m*=0.26m0，m0为电子静质量，即ωc和外加磁场的强度成正比，ωp=6.465 1×1011Hz为N掺杂硅中电子的等离子体共振频率，采用归一化频率ωp=1.001 (2πc/a)，a为晶格常数，ω为光的频率。图1为N型半导体硅圆柱ωc=0.25ωp、0.15ωp和ωc=-0.25ωp、-0.15ωp时的相对介电参数ε+ε-。从图1a和图1b可以看出，在不同的ωc下，N型半导体硅的不同光频率所对应的相对介电参数可以相差很大。

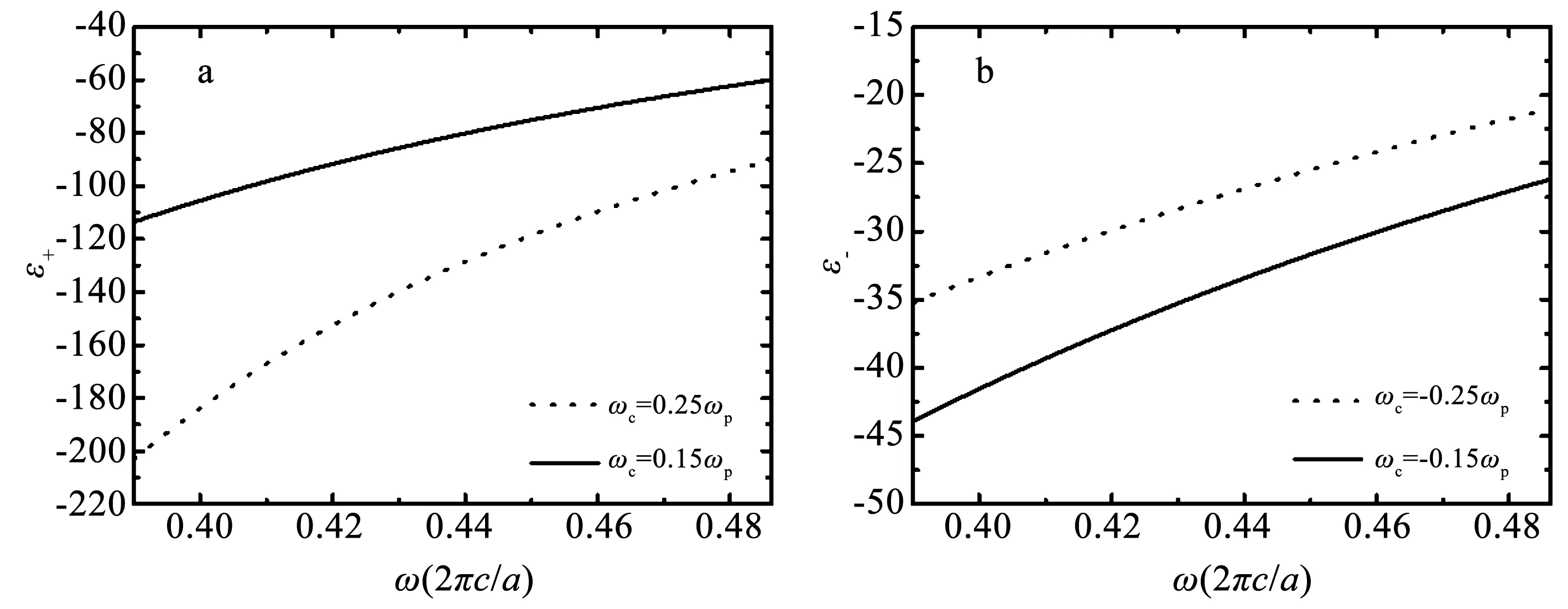
图1　N型Si的相对介电参数ε+和ε-Fig. 1　Relative permittivity ε+ and ε- of N-type Si

硅圆柱按照图2a所示正方晶格排列在空气中，晶格常数a为2.9156 mm，r为硅圆柱的半径，占空比(πr2/a2)为0.3632,并假定其平行于Z方向且长度无限长。如果从中抽取一根硅圆柱就构成光子晶体点缺陷。图2b为相应的第一布里渊区。模拟时首先设定ωc=0.25ωp、-0.25ωp，采用专门针对偏微分方程组求解的有限元分析软件COMSOL进行模拟。COMSOL软件基于有限元法将如图2a所示光子晶体结构的原胞离散为若干个求解区域，并通过求解区域交界面上的结点相互连接成组合体。每个求解区域内的近似函数由未知场函数在求解区域各个结点上的数值和与其对应的插值函数来表达。利用和原问题数学模型等效的变分原理或加权余量法，建立求解基本未知量的代数方程组或常微分方程组。最后用数值方法求解方程。对于光子晶体的能带和模式分布的求解，COMSOL不需要编制复杂的偏微分方程组的求解器，只需要将方程中各变量在软件界面中一一对应即可求解[18]。

图2　二维完美正方晶格光子晶体的横截面a及其相对应的第一布里渊区bFig.2　Transverse cross section of perfect square lattice PCs and its corresponding first Brillouin zone

图3　二维完美光子晶体的能带结构Fig.3　Band structure of 2D perfect PCs

图4　光子晶体点缺陷的能带和ωc=0.25ωp时第一缺陷模式的场分布Fig.4　Band structure of a point defect and first defect mode field distribution at ωc=0.25ωp

图3为模拟得到的完美光子晶体沿图2b所示ΓΧ和ΓΜ方向的前三条能带。在M点，第一和第二条能带之间的带隙宽度ω±分别为0.200 79(2πc/a)和0.092 99(2πc/a)。可以看出，ωc=0.25ωp时形成的带隙宽于ωc=-0.25ωp。虽然在两种情形下，光子晶体的结构参数完全一致，但是由于法拉第效应，硅圆柱的相对介电参数有较大差别，这就造成了光子晶体能带的移动和带隙宽度的变化。在完美光子晶体的内部去除一根硅圆柱得到点缺陷腔，图3给出了相应的能带和ωc=0.25ωp时的第一缺陷模式的电场Ez的场分布。从图4可以看出，新出现的三个缺陷模式的频率均低于完美光子晶体的最低能带的频率。ωc=0.25ωp时形成的缺陷模式频率ω+(0.434 47、0.639 59和0.639 59(2πc/a))比ωc=-0.25ωp时形成的缺陷模式频率ω-(0.461 19、0.682 46和0.682 46(2πc/a))略低，后两个模式是简并的偶极模式。两种情形下，第一缺陷模式之间的频率差比第二缺陷模式之间的频率差小，其他对应模式也存在这一现象。如图5所示ωc=0.25ωp时的第一缺陷模式的电场主要是局域在点缺陷里面，ωc=-0.25ωp时的电场分布与其类似。

如果只考虑最近邻点缺陷的耦合，耦合腔光波导的群速度与点缺陷的局域模式的频率和相邻点缺陷的耦合强度有关，所以，通常降低耦合腔光波导的群速度的做法是增大相邻点缺陷之间的距离、选用其他缺陷模式等方法。为了获得较低的群速度，下文模拟时设定相邻点缺陷之间的距离为三倍晶格常数，也即以3a为重复单元。如图5所示，ωc=0.25ωp时第一缺陷模式ω+的频率为0.436(2πc/a)，由公式(1)可知其对应的体材料Si的ε+为-132.8679,群速度变为9.9×10-4c。ωc=-0.25ωp时第一缺陷模式ω-的频率为0.457 986 962(2πc/a)，由公式(1)可知其对应的体材料Si的ε-为-30.369 45,群速度变为2.088×10-4c。这一结果和其他报道的最优结果相当[19]，证实了基于法拉第效应降低半导体光子晶体耦合腔光波导群速度的有效性，同时群速度还可以通过优化占空比等方法进一步降低。虽然这两种缺陷模式频率对应的体材料硅的相对介电参数为负值，但是群速度vg代表能量传播的方向，因此光仍可以在波导中传播。

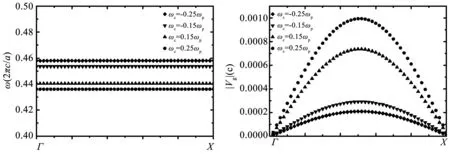
图5　耦合腔光波导的能带和相应的群速度Fig.5　Band structure and its corresponding group velocity of coupled-resonator optical waveguide

3结论

本文主要研究了半导体材料构成的点缺陷和耦合腔光波导的可调谐性能。模拟发现第一缺陷模式的频率低于完美光子晶体的最低频率，同样也会随着外加磁场的变化而发生移动，这就为调控耦合腔光波导的群速度提供了可能。通过模拟以3a为重复单元的耦合腔光波导的能带，证实逆着光传播的方向施加磁场可以获得2.088×10-4c的群速度。半导体光子晶体耦合腔光波导中传播模式的频率恰好处在太赫兹频段，这就为如何在太赫兹或更低频段设计集成的半导体光子晶体探测器，以实现常温下直接探测太赫兹波提供了新思路。

参考文献：

[1]YABLONOVITCH E. Inhibited spontaneous emission in solid-state physics and electronics[J]. Physical Review Letters. 1987, 58(20)： 2059-2062.

[2]JOHN S. Strong localization of photons in certain disordered dielectric superlattices[J]. Physical Review Letters,1987, 58(23)：2486-2489.

[3]HOSSEINI S, JAMSHIDI K. Modulation efficiency enhancement of an optical phase modulator using one dimensional photonic crystal structures[C]//SPIE OPTO. [S.L.]:International Society for Optics and Photonics, 2015: 93670I-93670I-6.

[4]MAKTOOBI S, BAHADORI-HAGHIGHI S. Investigation and simulation of photonic crystal directional coupler switch[J]. Electronics Letters, 2015, 51(13): 1016-1018.

[5]LIN T, ZHANG X, ZOU Y, et al. Out-of-plane nano-electro-mechanical tuning of the Fano resonance in photonic crystal split-beam nanocavity[J]. Applied Physics Letters, 2015, 107(15): 153107.

[6]MENG Q B, FU C H, HAYAMI S, et al. Effects of external electric field upon the photonic band structure in synthetic opal infiltrated with liquid crystal[J]. Journal of Applied Physics, 2001, 89(10): 5794-5796.

[7]ELSAYED H A, EL-NAGGAR S A, ALY A H. Thermal properties and two-dimensional photonic band gaps[J]. Journal of Modern Optics, 2014, 61(5): 385-389.

[8]PORRAS-MONTENEGRO N, DUQUE C A. Temperature and hydrostatic pressure effects on the photonic band structure of a 2D honeycomb lattice[J]. Physica E: Low-dimensional Systems and Nanostructures, 2010, 42(6): 1865-1869.

[9]DUQUE C A, PORRAS-MONTENEGRO N, CAVALCANTI S B, et al. Photonic band structure evolution of a honeycomb lattice in the presence of an external magnetic field[J]. Journal of Applied Physics, 2009, 105(3): 034303.

[10]TZUANG L D, FANG K, NUSSENZVEIG P, et al. Non-reciprocal phase shift induced by an effective magnetic flux for light[J]. Nature photonics, 2014, 8(9): 701-705.

[11]JIANG B, ZHANG Y, WANG Y, et al. Magnetically controlled photonic crystal binary digits generator[J]. Applied Physics Letters, 2012, 101(4): 043505.

[12]HE C, CHEN X L, LU M H, et al. Tunable one-way cross-waveguide splitter based on gyromagnetic photonic crystal[J]. Applied Physics Letters, 2010, 96(11): 111111.

[13]WANG Z, CHONG Y D, JOANNOPOULOS J D, et al. Reflection-free one-way edge modes in a gyromagnetic photonic crystal[J]. Physical review letters, 2008, 100(1): 013905.

[14]FAN C Z, WANG G, HUANG J P. Magnetocontrollable photonic crystals based on colloidal ferrofluids[J]. Journal of Applied Physics, 2008, 103(9): 094107.

[15]ALY A H, EL-NAGGAR S A, ELSAYED H A. Tunability of two dimensional n-doped semiconductor photonic crystals based on the Faraday effect[J]. Optics express, 2015, 23(11): 15038-15046.

[16]CHEN X, LIU H, LI Q, et al. Terahertz detectors arrays based on orderly aligned in N nanowires[J]. Scientific reports, 2015, 5: 13199.

[17]YARIV A, XU Y, LEE R K, et al. Coupled-resonator optical waveguide: a proposal and analysis[J]. Optics letters, 1999, 24(11): 711-713.

[18]孙培德，杨东全，陈奕柏. 多物理场耦合模型及数值模拟导论[M]. 北京：中国科学技术出版社，2007:146-146.

[19]李长红,万勇,毛强明. 椭圆柱微腔光子晶体耦合腔波导的慢光特性研究[J]. 光学学报, 2015, 35(4): 0416002.

DOI:10.3976/j.issn.1002-4026.2016.03.019

收稿日期：2015-03-23

基金项目：潍坊学院博士基金(2014BS01)；潍坊科技发展计划(2015GX022)；国家自然科学基金青年科学基金(61404093)

作者简介：孙海竹(1986-)，女，助教，研究方向为光子晶体及其器件。 *通讯作者。Email:zhjx_aa@126.com

中图分类号：TN252

文献标识码：A

文章编号：1002-4026(2016)03-0110-05

Tunability of Faraday Effect to group velocity of N-doped silicon coupled-resonator optical waveguide

SUN Hai-zhu, ZHANG Jian-xin*, HAN Kai, HUANG Bao-xin

(Department of Physics and Electro-Optical Engineering, Weifang University, Weifang 261061, China)

Abstract∶Coupled-resonator optical waveguide is implemented through mutual coupling of defect mode of point defects of photonic crystals, and group velocity is its important parameter. We simulate band structures of N-doped silicon coupled-resonator optical waveguide. Simulation results show that if N-doped silicon Faraday Effect based magnetic field is applied against the direction of light propagation, relative permittivity at the frequency of the defect mode will decrease. The group velocity will also decrease to 2.088×10-4c. We therefore confirm regulation of Faraday Effect to waveguide group velocity. Such discovery provides a new and effective way for implementation of slow light effect at terahertz or even lower bands.

Key words∶photonic crystal; coupled-resonator optical waveguide; group velocity; THz band