相速度和群速度超光速问题再辨析
2022-07-12费兆宇马宇翰孙昌璞
费兆宇 马宇翰 孙昌璞,2
(1.中国工程物理研究院研究生院 100193;2.北京计算科学研究中心 100193)
波是物理学中的基本概念之一。作为描述波传播的物理量,相速度和群速度在物理学的科研与教学中扮演十分重要的角色。物理及相关专业的本科生最早会在力学部分的振动与波章节中接触到这两个概念,此后还会在光学、电磁学、电动力学、固体物理等专业课程中进一步学习与讨论它们。
在自然界中,光的相速度和群速度在某些条件下可以超过真空中的光速c(以下简称光速)。然而这种超光速现象并不能传递信息,因而不会破坏狭义相对论所要求的因果律。具体来说,相速度和群速度能否超光速,取决于波传播的介质的色散关系。例如,在折射率小于1的介质中,波的相速度可以超过光速;而在反常色散介质中波的群速度也可以超过光速。这一事实在此前的一些教材①②和文献中③④已经有明确的说明。
然而,在日常科研和教学中,笔者发现仍然有不少人认为波的相速度或群速度是不可能超过光速的。最近,我们调查了本课题组的学生(包括正在实习的本科生)和博士后共计23人对此问题的理解。结果显示,17.4%的人认为群速度和相速度都可以超光速;60.9%的人认为相速度可以超光速而群速度不能超光速,因为他们认为群速度代表信息传播的速度;还有21.7%的人认为群速度和相速度都不能超光速。我们小范围抽样的结果意味着,大多数物理专业的学生对这一问题的认知可能仍然存在误区。本文将从几个具体例子出发,讨论波的相速度和群速度在什么条件下可以超光速,旨在厘清在物理教学中可能存在的关于相速度和群速度能否超光速问题的误区。
1.相速度超光速
根据麦克斯韦方程组(Maxwell’s equations),在均匀稳态非耗散介质中传播的电磁波满足波动方程
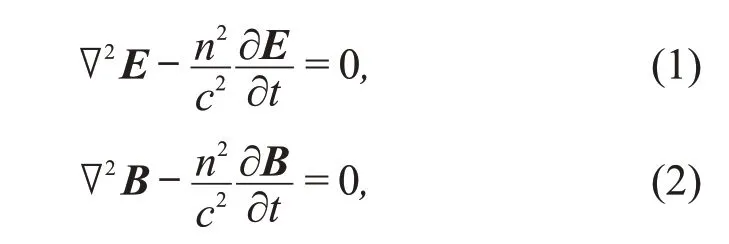
其中,E为电场强度,B为磁感应强度,n为介质的折射率⑤。考虑沿x方向传播的圆频率为ω,波数为k的单色平面波解u(x,t)=u0eikx-iωt(u(x,t)的实部为E或B沿垂直于波传播方向的分量),代入上述波动方程后得

u(x,t)的等相位点满足kx-ωt=常数,这样可以定义等相位点的速度vp,即相速度为

在有色散的介质中,折射率n和圆频率ω都是波数k的函数,且通常n >1。因此,相速度vp <c。而相速度超光速常见于以下两种情形。
(1)折射率小于1介质中的超光速
当电磁波的频率接近介质的共振频率时,会发生共振吸收。此时,介质的折射率可以小于1(见图1)。另外,当电磁波的频率超过介质的最高共振频率时,折射率也会小于1。例如,北京玻璃研究所提供的一种单管材料对波长为1.238 nm 的X 光的折射率为0.9995358④。这种超光速并不违反因果律(即信息的传播不会超过光速)。具体来说,由于单色平面波必须是无限延展的,且波的频率和振幅为常数,因此它不能携带信息。
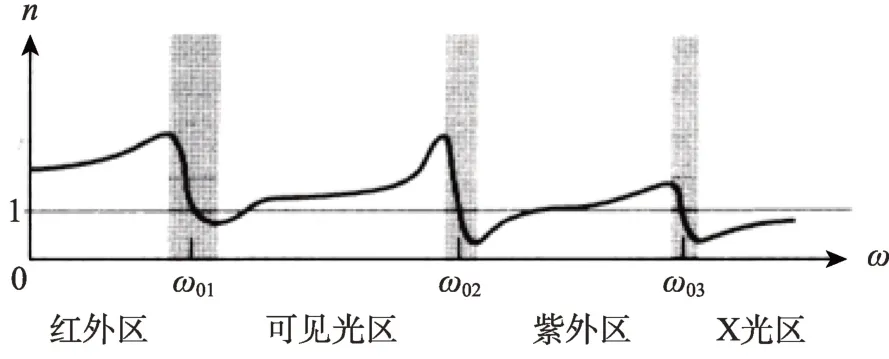
图1 介质中的折射率示意图(图摘取自文献②)
(2)波导中的超光速
由于边界条件的限制,即使是在真空中传播的电磁波仍然能够超光速。考虑在中空金属柱体内传播的电磁波(即波导,见图2),其色散关系如下①⑥

图2 矩形波导示意图(图摘取自文献⑥)

其中ωc是波导内传播的波的最低频率,称为截止频率。
根据式(4),波的相速度为

必定大于c,并且当ω →ωc时,相速度会趋于无穷大。这种超光速并不违反因果律,这是因为在波导中信息传递的速度是群速度vg(见下节)。可以证明,在无介质波导中波的相速度和群速度满足的关系为①因此相速度超光速必然导致群速度小于光速。

2.群速度超光速
为了使电磁波能够携带信息,在实际应用中,总会对波的频率和振幅进行调制。此时的电磁波是各种单色波的线性组合,即①
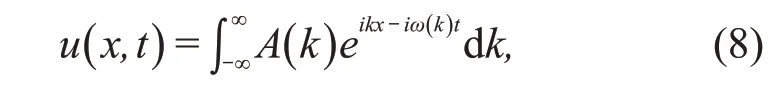
其中A(k)是展开系数。如果A(k)是以波数k0为中心的相当尖锐的峰形曲线(如图3),那么可以把圆频率ω(k)在k0附近做微扰展开

图3 A(k)的峰形曲线示意图①

其中ω0=ω(k0)。
将式(9)带入式(8)后,我们得到

上式表明,除了一个总相位之外,波的包络以群速度vg行进

并且其形状不发生畸变。如果波的包络在行进过程中发生了畸变,那么就需要考虑式(9)中高阶项的贡献。此时,群速度vg只是由式(11)定义的速度,而不能被认为是信息的传播速度。
根据式(4),群速度vg还可以用折射率n(ω) 来表示
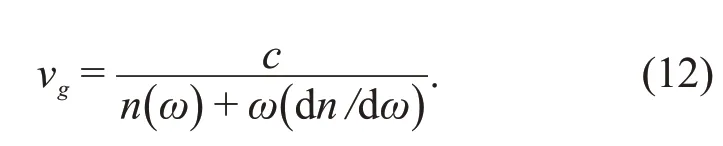
对于正常色散来说,(dn/dω)>0,且通常n>1,这时群速度小于相速度,并且也小于c。但是,在反常色散区域中,dn/dω为负值,且绝对值可以很大。这时群速度就可以大于c,甚至可以为负值。
需要注意的是,这种超光速并不违反因果律。由于(dn/dω)很大,ω随k的变化很快,因此式(9)的近似不再成立,波的包络在行进中会发生畸变①。这样一来,群速度在这里不再是一个有意义的概念。在下一节关于实验“增益超光速光脉冲传播”⑦的讨论中,我们会更具体地解释群速度超光速和负群速度的物理现象。事实上,光信号的传播速度与相速度和群速度都没有必然的联系。A.Sommerfeld 和L.Brillouin 曾对信号的传播速度进行过细致的讨论。他们的结论是信号的传播速度不能超过c①⑧。
3.实验中观测到负群速度和超光速现象
2000 年,普林斯顿高等研究院的王力军(现为清华大学物理系、精密仪器与机械学系双聘教授)等人在英国《自然》杂志上发表了文章“增益超光速光脉冲传播”⑦,报道了他们的测量结果:铯原子气体在反常色散区域的群速度是-c/310,进入铯原子气体的光脉冲比真空中的光脉冲超前62 ns通过气体池。
在这项实验中,研究人员利用泵浦光技术,使得实验中的铯原子气体表现出了如下的光学特性:不同频率的光在其中会有不同的增益和不同的速度。图4是实验中测得的铯原子气体中光的振幅的增益系数以及折射指数(即折射率)随光波频率的变化曲线。利用折射率反常色散区域的测量结果(对应图4 中增益系数双峰之间的区域),根据式(11)计算出群速度为-c/(330±30)。该计算结果与实验测量结果在误差范围内一致。图5是两个高斯光脉冲通过气体池后的强度随时间的变化。其中,曲线A 为以光速c行进的光束,曲线B 为探测光束。可见探测光束比真空中的光束超前62(±1) ns 通过气体池,即发生了超光速现象。

图4 光的振幅的增益系数以及折射指数随光波频率的变化曲线(图摘取自文献⑨)

图5 两个光脉冲通过气体池后的强度随时间的变化(图摘取自文献⑨)
实验中的负群速度和超光速现象一经发现就引起了众多物理学家的研究兴趣⑨-⑱。虽然大家分析这些现象的角度各不相同,但是结论都表明上述超光速现象并不会导致光信号超光速。我们接下来介绍文献⑩对该实验现象的理论解释。图6左侧是对负群速度现象的模拟示意图,模拟时取vg=-c/2 和c=1,t=0 为高斯光束的峰值到达气体池左边界的时刻。从图中可以看出,由于增益介质的性质,虽然探测光束还没有到达气体池左边界,但是在气体池的右边界处已经出现了两束光脉冲。其中气体池内部的光束以群速度c/2 向左运动,并在气体池左边界处与探测光相干相消。而气体池外部的光束,则以群速度c向右运动。如果将测量仪器放在气体池右侧,那么就可以探测到超光速的光脉冲。

图6 (a)负群速度现象的模拟示意图。z为空间位置,E为光束的电场强度。模拟时取vg=-c/2 和c=1;(b)(a)图中电场强度取对数后的结果(图摘取自文献⑩)
这种超光速现象之所以不违反因果律,是因为将0时刻视为光信号到达气体池左边界的时刻实际上是一种误解。将图6(a)中的数据取对数(即图6(b))后就能发现,早在0 时刻之前,光束的前端就已经穿过了气体池。因为此时,探测光束已经发生了明显的变形,存在多个峰值,这就是第二节中所讨论的波包畸变现象。此时将峰值的运动速度(即群速度)视为光信号的传播速度显然是错误的,进而该超光速现象也不能被视为光信号的超光速传播。
4.小结
本文从几个具体例子出发,详细讨论了电磁波的相速度和群速度的超光速问题。例如,在以下两种情况中相速度可以超光速:a)介质的折射率小于1;b)在波导中传播的电磁波。另外,在介质的反常色散区域,dn/dω为负值,且绝对值很大时,群速度可以超光速,甚至可以为负值。需要注意的是,由于电磁波信号的传播速度与相速度和群速度都没有必然的联系,因此这些超光速现象并不违反因果律。
通过整理、介绍和分析几个相速度和群速度超光速的示例,笔者希望本文的论述能纠正广泛存在的关于相速度或群速度不能超光速这一错误认知,并对相关物理课程的教学起到一定的启发作用。
致谢:感谢课题组成员田西城同学对本文的仔细阅读与建议。本研究受国家自然科学基金(批准号:12088101),NSAF基金-科学研究中心项目(批准号:U1 930403;U1930402),中国博士后科学基金(批准号:BX2 021030;2021M700359)的资助。
