捕捉激波的群速度控制方法

李新亮，傅德薰，马延文

（中国科学院力学研究所 高温气体动力学国家重点实验室，北京 100190）

捕捉激波的群速度控制方法

李新亮，傅德薰，马延文

（中国科学院力学研究所 高温气体动力学国家重点实验室，北京 100190）

回顾及综述了群速度控制方法基本原理、发展过程及最新进展。群速度控制方法是通过控制色散误差以捕捉间断的一种数值方法。该方法通过在间断两侧采用不同色散类型的格式，将数值波的传播压制在间断附近，避免数值振荡向周围扩散，从而达到抑制数值振荡的效果。该方法主体上采用数值色散抑制振荡，实际使用中仅需补充较低水平的数值耗散就可将振荡压制在可接受的范围内。因而群速度控制格式的总体耗散水平较低，易于实现小尺度波的高分辨率捕捉，是复杂流动高分辨率数值模拟的有效方法。

群速度控制格式；激波捕捉格式；高分辨率；色散；耗散

0 引 言

高精度激波捕捉方法在计算流体力学领域占有重要地位。该方法要求具有较高的间断分辨率（即，数值解间断尽量锐利），且间断周围数值振荡尽量小，而在非间断区（光滑区）需具有较高的数值精度及分辨率［1］。传统意义上讲，不低于二阶精度的激波捕捉方法均可称为高精度激波捕捉方法。代表性的高精度激波捕捉格式有TVD格式［2］，NND格式［3］，WENO格式［4］以及高阶保单调格式［5］等。这些格式在光滑区（非间断区）采用较高数值精度及较低数值耗散的方法，以保证较高的数值分辨率，而在间断附近则采用较低数值精度及较高数值耗散的格式以抑制数值振荡。这些差分格式大多是通过数值粘性压制数值波的传播，从而起到抑制振荡的效果。

群速度控制方法（Group Velocity Control Method，GVC）是傅德薰等人提出的一种新型激波捕捉方法［6-7］，与TVD及WENO等格式的机制不同，该格式并不直接通过耗散机制抑制激波，而是通过色散控制捕捉激波。该格式利用色散误差控制数值波传播的群速度，使得数值传播的方向指向间断，以避免从间断发出的数值振荡污染流场。由于采用数值色散抑制振荡，因而群速度控制格式总体上数值耗散较小。且该方法实现简洁，其计算量明显低于WENO等高精度激波捕捉方法。利用该思想，先后构造了紧致型群速度控制格式［8］，优化型群速度控制格式［9］，加权型群速度控制格式［10］以及助波器型群速度控制格式［11，7］等多种群速度控制格式，为含间断复杂流动的数值模拟提供了有效的高分辨率计算方法。

1 群速度控制方法的基本思想

1.1 数值波的群速度：快格式、慢格式和混合格式

以线性对流方程

为例，讨论数值波的群速度。

对于方程（1），假设初值为如下单波：

u（x，0）＝eikx

其中

为修正波数。对于给定的线性格式，该修正波数可以通过理论分析得到［12］。而对于非线性格式，该修正波数的特性也可通过数值方法近似获得［13-14］。

该修正波数的虚部ki＝ki（α）反应了格式的色散误差，即数值波传播的相位（或波速）误差。当ki（α）＝α时，数值波传播速度与精确解相同；当ki（α）＞α时，数值波传播快于精确解；反之，则慢于精确解。而对于一般情况，数值解中包含了多个波的传播，因而观测到波传播的速度通常为波包的速度，即波的群速度，该群速度定义为［6-7］：

在整个波数范围内（0＜α≤π），D0（α）＞0的格式称为“快格式”，对于快格式，数值波传播的群速度超过精确解；在整个波数范围内D0（α）＜0的格式称为“慢格式”，对于慢格式，数值波传播的速度低于精确解；在部分波数范围内D0（α）＞0，在另外部分波数范围内D0（α）＜0的格式称为“混合格式”。图1给出了某些差分格式的群速度D0（α）＝dki／dα，从中可以看出2阶中心格式以及6阶对称紧致格式为“慢格式”；2阶迎风格式以及5阶迎风紧致格式为“混合格式”，这两种格式在低波数范围内具有“快格式”特征。

图1 某些差分格式的群速度［6］Fig.1 Group velocities for four finite difference schemes［6］

1.2 数值振荡产生原因及群速度控制的基本思想

群速度控制理论将间断周围数值振荡的原因归结为由色散误差导致的群速度误差。假设方程（1）的初值具有间断，则根据Fourier分解，该间断可分解为不同波数波的叠加，如图2所示。如果利用快格式进行数值计算，这些数值波传播的速度均快于理论速度a，而且不同波传播的群速度不同，通常情况下高波数成分的传播群速度更快。经过一段时间后高波数成分传播到了主波（间断）的前方，在间断前方形成了数值振荡，而波后振荡不明显。同样，利用慢格式计算时，所有数值波传播的速度均低于理论速度a，但高波数成分传播得更慢，因而数值解解在波后有明显振荡，而波前振荡不明显。

因而，如果混合使用“快格式”和“慢格式”，在波前使用“慢格式”，在波后使用“快格式”，则可以尽量压缩数值振荡的传播范围，从而起到抑制数值振荡的作用。这就是群速度控制的基本思想［6-7］。

图2 间断分解为若干波的叠加Fig.2 Diagrammatic sketch for the decomposition of a discontinuity

实际情况中，纯粹的“快格式”很难构造，而多数格式为混合型格式（如图1所示）。很多情况下利用低波数区为“快格式”的“混合格式”来代替纯“快格式”。这种情况下，由于这些“混合格式”在高波数范围具有“慢格式”特征，会影响群速度控制的效果。但通常这些格式在高波数区具有较强的数值粘性，具有抑制振荡效果，因而数值振荡通常会被压制在允许范围内。

2 群速度控制方法的具体实现及应用

2.1 二阶精度的群速度控制格式

在文献［6］中，傅德薰等除了介绍了群速度控制的基本思想，还给出了一种具有二阶精度的群速度控制格式，这是最早的群速度控制格式。该格式利用2阶迎风型格式作为“快格式／混合格式（MXD）”，利用二阶中心格式作为“慢格式（SLW）”。此外，该方法利用激波形状函数（Shock-Structure function，简称SS函数）判断激波前与激波后。SS函数的定义为：

对于向右传播的间断波，SS（u）＝－1为波前；SS（u）＝1为波后。图3为数值解中间断波的示意图，图中标示了SS函数如何区分波前和波后。

对于正通量，该二阶精度群速度控制格式的数值通量为：

其中：

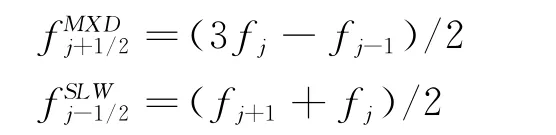
分别为作为“快格式／混合格式”使用的二阶迎风格式以及作为“慢格式”使用的二阶中心格式的数值通量。SS函数的值可由式（4）数值离散给出。

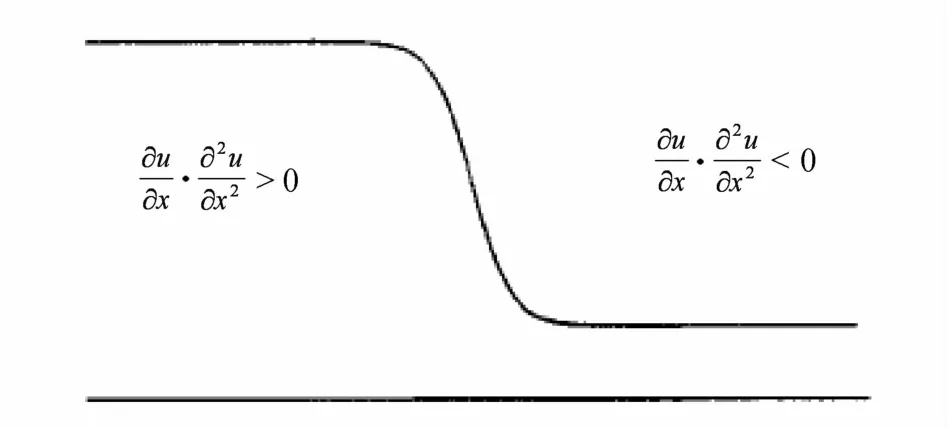
图3 数值解中传播的间断波示意图［8］Fig.3 Diagrammatic sketch for a N-Sshock［8］

2.2 紧致型群速度控制格式

在文献［8］中，马延文和傅德薰利用文献［6］的群速度思想，构造了紧致型群速度控制格式。该方法利用文献［6］的三阶迎风紧致格式作为“快格式”（实际上，该格式为混合格式，但在低波数范围内呈现快格式特征）；利用四阶中心紧致格式［12］作为“慢格式”。利用以上两种基础格式，构造出一种含自由参数的紧致型差分格式［7-8，15］：

其中Fj／Δx是函数∂f／∂x的逼近式，

分别为一阶及二阶导数中心差分算子。σ为自由参数。显然，当σ＝0时，格式为四阶对称紧致差分（“慢格式”）；当σ＝±1／6时，格式为三阶迎风紧致差分（“快格式／混合格式”）。通过调节该自由参数的数值，在激波（间断）前实现慢格式，在激波（间断）后实现快格式，从而实现群速度控制。

对于正通量，紧致型群速度控制格式的具体表达式如下［8］：

其中

1≤σ0≤2，0.8≤γ0≤1是格式中的常数。δ－fj＝fjfj－1，δ＋fj＝fj＋1－fj是向后、向前差分算子。P和c分别为当地的压力及声速，利用这两个参数的目的是探测激波的强度，并由此强化或弱化σ的变化范围。

对于负通量的紧致型群速度控制格式同理构造，具体表达式见文献［8］。

图4为采用该群速度控制格式计算Sod激波管问题，得到i＝0．14时刻的流场分布图（图片引自文献［8］）。从中可以看出，该计算具有很高的激波分辨率及较低的数值振荡水平。从该格式的表达式可以看出，格式并没有人为添加额外的数值耗散。计算结果显示，格式的整体耗散保持在较低的水平，大致与迎风紧致格式持平，但激波捕捉能力得到了很大提升。需要指出的是，在文献［8］中，并没有利用到局部特征分解，而是直接基于Steger-Warming分裂后的通量进行差分计算。如果利用了局部特征分解，则激波附近的数值振荡还可以进一步降低［16］。

图4 Sod激波管问题t=0.14时刻的流场分布［8］Fig.4 Distributions of flow at t=0.14 of Sod problem［8］

2.3 八阶精度的优化型群速度控制格式

在文献［9］中，李新亮等利用群速度控制思想，构造了八阶精度的普通型（非紧致）群速度控制格式（GVC8）。在格式的构造过程中还采用了基于算例的优化技术，针对具体算例（Sod激波管问题），以鲁棒性为目标，对格式的系数进行优化，从而在保证计算精度及激波分辨率的情况下，提高了方法的鲁棒性。

针对方程（1），构造线性差分格式：

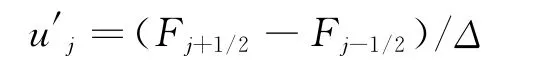
其中：

格式使用9个网格点构造数值通量，理论上最高可具有9阶精度。GVC8要求格式具有8阶精度，因而，有一个参数可以自由调节。通过优化调节该系数，得到两组不同的线性差分格式，使得一组为“快格式”（实际上是混合格式），另外一组为“慢格式”。在格式的构造过程中，系数的优化除了考虑格式的群速度特性，还根据算例进行了系数优化，使得格式具有更好的鲁棒性。

在该格式采用更为简洁的判据以判断某点位于激波的前方还是激波的后方。判据为：对于向右传播的波，如果|uj－uj－1|＜|uj＋1－uj|，则认为该点（j点）位于波后，否则，则认为该点位于波前。如示意图5所示，通常情况下，越靠近激波（间断），数值振荡越激烈，因而振荡（变差）大的方向为激波所在的位置。

图5 激波附近数值解示意图Fig.5 Diagrammatic sketch for numerical solution near a shock

对于正通量（方程（1），a＞0），GVC8格式为式（6），格式的系数为：

系数的具体值如表1［9］。

表1 的值［9］Table 1 Values of［9］

文献［9］通过Shu-Osher问题以及可压缩各向同性湍流DNS对该格式进行了测试，结果显示，该格式具有较低的数值耗散及较高的尺度分辨率。此外，该格式的另外一个优点是构造简洁，计算量小。数值测试显示，其计算量接近9阶精度的线性格式，远低于5阶精度的WENO格式。该格式的不足是鲁棒性略弱，尤其是对于高Mach数的算例。

2.4 加权型群速度控制格式（WGVC）

利用群速度控制思想，何志伟等人构造了加权群速度控制格式（WGVC，Weighted Group Velocity Control Scheme）［10］，并进一步构建了WGVC-WENO混合格式，提升了格式的鲁棒性。

WGVC格式离散的正通量表达式为：

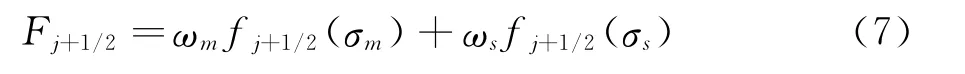
其中fj＋1／2（σ）是含有自由参数σ，且经过优化的线性格式。随着参数σ的变化，该格式可以表现出“慢格式”以及“混合格式／快格式”的特性。两个自由参数σm和σs以及权重ωm、ωs根据流场特性数值计算产生［10］。在波前区，σs≈1，σm≈0，格式（7）表现出“慢格式”特征；反之在波后区格式表现出“混合格式／快格式”特征。格式的群速度特性由参数σm和σs根据流场的光滑性质自适应给出。在此基础上，何志伟等人构造了WGVC-WENO混合格式，在间断区借助WENO格式提升格式的鲁棒性。图6为Shu-Osher问题的计算结果（201网格点），从中可以看出，与7阶WENO格式相比，7阶精度的WGVC-WENO混合格式具有更好的数值分辨率。

2.5 群速度助推法

在文献［11］中，马延文等提出了一种群速度助波器（Group Velocity Booster，GVB），可将常规线性差分格式改造成群速度控制格式。

对于微分方程：

图6 Shu-Osher问题计算结果：WGVC-WENO7 vs.WENO7，201网格点［10］Fig.6 Distributions of density for Shu-Osher problem：WGVC-WENO7 vs.WENO7，201 points［10］

其中Dh为“慢格式”型差分算子。实际上，很多迎风型差分算子为慢格式（例如三、五、七阶迎风偏心型差分）［7］。通过添加“助波器”，可将式（8）改造成群速度控制格式。改造后的格式为：

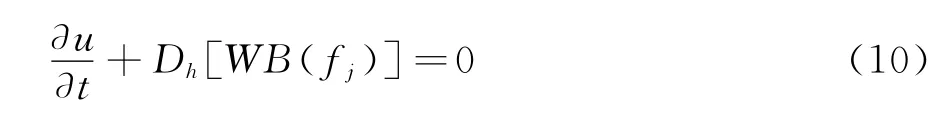
其中，算子WB为群速度助波器，通过添加该助波器，可以将原先的“慢格式”改造成群速度控制格式。常见的助波器形式为［7，11］：

2.6 其他群速度控制格式

除了前文介绍的方法，还有很多研究者利用群速度控制思想进行了激波捕捉格式的构建及应用。

Zhu等人［17］运用群速度控制思想并结合系数优化，构建了紧致型群速度控制格式，并通过飞船返回舱高速绕流算例进行了测试。结果显示，该方法具有较好的鲁棒性及激波分辨率。周超红等人［18］利用群速度控制思想，构造了三阶及四阶精度的群速度控制格式，并将该方法推广到求解浅水波方法，数值实验表明，该方法可以很好地控制非物理振荡并能保证计算精度。田保林等人［19］根据数值解的群速度特性，在三阶迎风紧致格式的基础上引入了群速度控制机制，使其能够正确模拟含有强激波和强接触间断的复杂流动。计算结果表明，该方法对激波和接触间断的分辨效果是令人满意的。Cheng等人［20］在原群速度控制格式的基础上，进一步减小了数值耗散，构造了一种低耗散的群速度控制格式。高慧等人构造具有六阶精度的紧致型群速度控制差分格式［21］，并通过Sod激波管问题、定常激波问题以及二维激波反射等问题进行了测试，结果显示，该方法具有网格基架点小和捕捉激波能力较强的优点。

3 结论及展望

低耗散、高分辨率激波捕捉方法是近年来计算流体力学领域研究的热点。群速度控制方法则是近年来提出的一种新型的激波捕捉方法。不同于大多数通过耗散压制数值振荡的方法，群速度控制方法主张通过控制色散误差抑制数值振荡。该方法根据数值波传播的特性，将格式区分为“快格式”和“慢格式”，并通过在间断前使用“慢格式”，在间断后使用“快格式”的方法，限制数值振荡的传播，从而起到抑制间断附近数值振荡的效果。由于该方法主体上采用数值耗散抑制振荡，实际使用过程中仅需再添加少量数值耗散就可将振荡抑制在可接受的范围内。因而，该格式的总体耗散水平较低，适用于多尺度复杂流动的高分辨率数值模拟。此外，与WENO等格式相比，群速度控制格式实现简单，计算效率较高。

群速度控制格式也有需要改进之处。通常情况下纯粹的“快格式”比较难于构造，因而经常使用“混合格式”代替“快格式”，这种情况下高波数振荡仍需要一定的耗散来压制。但由于大多数“混合格式”本身的耗散特性具有压制高波数振荡能力，因而通常状况下无需额外添加粘性（或仅需添加较弱的格式粘性即可）。此外，群速度控制格式的鲁棒性与WENO等格式相比仍略显不足，这可以通过构建混合型格式等方法来弥补。相信随着数值计算技术的完善和发展，群速度控制格式也会逐渐发展并会获得较好的应用。

致谢：感谢国家超级计算天津中心，中国科学院网络中心超级计算中心以及国家超级计算济南中心提供计算机时。

［1］PIROZZOLIS．Numerical methods for high-speed flows［J］．Annual Review Fluid Mechanics，2011，43：94-163．

［2］HARTEN A．High resolution schemes for hyperbolic systems of conservation laws［J］．Journal of Computational Physics，1983，49：357-393．

［3］张涵信．无波动、无自由参数的耗散差分格式［J］．空气动力学报，1988，6（2）：143-164．

［4］JIANG G S，SHU C W．Efficient implementation of weighted ENO schemes［J］．Journal of Computational Physics，1996，126：202-228．

［5］SURESH A，HUYNH H T．Accurate monotonicity-preserving schemes with runge-kutta time stepping［J］．Journal of Computational Physics，1997，136：83-99．

［6］FU D X，MA Y W．A high order accurate difference scheme for complex flow fields［J］．Journal of Computational Physics，1997，134：1-15．

［7］傅德薰，马延文，李新亮，等．可压缩湍流直接数值模拟［M］．科学出版社，2010．

［8］MA Y W，FU D X．Fourth order accurate compact scheme with group velocity control（GVC）［J］．Science in China A，2001，44（9）：1197-1204．

［9］LI X L，FU D X，MA Y W．Optimized group velocity control scheme and DNS of decaying compressible turbulence of relativehigh turbulent Mach number［J］．International Journal for Numerical Methods in Fluids，2005，48：835-852．

［10］HE Z W，LI X L，LIANG X．Nonlinear spectral-like schemes for hybrid schemes［J］．Science China：Physics，Mechanics& Astronomy，2014，57（4）：753-763．

［11］MA Y W，FU D X，LI X L．A new high order accurate shock capture method with wave booster［C］．Proceeding of 2nd International Symposium on Computational Mechanics，Hong Kong and Macau，Nov 30-Dec 3，2009．

［12］LELE S K．Compact finite difference schemes with spectral-like resolution［J］．Journal of Computational Physics，1992，103：16-42．

［13］PIROZZOLI S．On the spectral properties of shock-capturing schemes［J］．J.Comput.Phys.，2006，219：489-497．

［14］LI X L，LENG Y，HE Z W．Optimized sixth-order monotonicity-preserving scheme by nonlinear spectral analysis international［J］．Journal for Numerical Methods in Fluids，2013，73：560-577．

［15］MA Y W，FU D X，Scheme construction with numerical flux residual correction（NFRC）and group velocity control（GVC）［J］．Progress in Natural Science，2006，16（12）：1252-1259．

［16］HE Z W，LI X L，FU D X，et al．Monotonicity-preserving upwind compact difference schemes［J］．Science in China G，2011，54（3）：511-522．

［17］ZHU Q Y，LI Y．An upwind compact approach with group velocity control for compressible flow fields［J］．International Journal for Numerical Methods in Fluids，2004，44（5）：463-482．

［18］ZHOU C H，YAO Q H，ZHU Q Y．The modified finite difference schemes with group velocity control for solving 2D shallow water equations［J］．ACTA Scientiarum Naturalium Universitatis Sungatseni，2012，51（1）：19-24．（in Chinese）

周超红，姚清河，朱庆勇．求解二维浅水波方程的群速度修正法［J］．中山大学学报（自然科学版），2012，51（1）：19-24．

［19］TIAN B L，FU D X，MA Y W．Group velocity control scheme and two-dimensional Riemann slover［J］．Chinese Journal of Computational Mechanics，2005，22（1）：104-108．（in Chinese）

田保林，傅德薰，马延文．群速度控制格式及二维Riemann解［J］．计算力学学报，

［20］CHENG J B，FU D X，MA Y W．Group velocity control scheme with low dissipation［J］．Chinese Journal of Aeronautics，2000，13（3）：138-145．

［21］GAO H，MA Y W，FU D X．Sixth order accurate compact scheme with group velocity control and application［J］．Journal of Aerospace Power，2003，18（1）：24-31．（in Chinese）

高慧，马延文，傅德薰．六阶精度的群速度直接控制紧致格式及其应用［J］．航空动力学报，2003，18（1）：24-31．

Review for group velocity control schemes

LI Xinliang，FU Dexun，MA Yanwen
（LHD，Institute of Mechanics，Chinese Academy of Sciences，Beijing 100190，China）

The basic principles and the recent developments of group velocity control（GVC）method are reviewed．GVC method is a new shock capture method by controlling the dispersion error of numerical schemes．In GVC method，the“fast”scheme is used in front of the shock and the“slow”one is used behind the shock，and in this way，the spread of numerical oscillations is limited in a very small region near the shock，and thus the oscillations are suppressed．The GVC method capture shock mainly by using dispersion technique，therefore，the dissipation of GVC schemes is relatively low．The recently developments of GVC schemes，such as compact GVC scheme，optimized GVC scheme，hybrid weighted GVC-WENO scheme and GVC scheme by group velocity booster，are also reviewed．GVC schemes are useful methods for detail simulation of multi-scale flows．

group velocity control；shock capture scheme；high resolution，dispersion；dissipation

V211.3

Adoi:10.7638／kqdlxxb-2014.0104

0258-1825（2014）05-0575-06

2014-08-20；

2014-09-10

国家自然科学基金（1372330，11472010，11472278）；863项目（2012AA01A304）；中国科学院知识创新工程项目（KJCX2-EWJ01，XXH12503-02-02-04）

李新亮（1972-），男，研究员，主要研究方向：计算流体力学，湍流．E-mail：lixl＠imech．ac．cn

李新亮，傅德薰，马延文．捕捉激波的群速度控制方法［J］．空气动力学学报，2014，32（5）：575-580．

10．7638／kqdlxxb-2014．0104． LI X L，FU D X，MA Y W．Review for group velocity control schemes［J］．ACTA Aerodynamica Sinica，2014，32（5）：575-580．