利用多重滤波法提取面波群速度及其高斯滤波参数取值

蒋婵君,王有学,熊 彬,王海燕

(1.桂林理工大学 a.地球科学学院; b.广西隐伏金属矿产勘查重点实验室,广西 桂林 541006;2.桂林理工大学博文管理学院,广西 桂林 541006)

天然地震面波层析成像是探测地壳和上地幔结构的最常用方法之一,其前提是从面波数据中提取高质量的相速度或者群速度。目前,提取面波群速度的方法有移动窗分析法[1]、多重滤波法[2]和连续小波变换[3],其中多重滤波法是提取面波群速度最常用的方法[4-9]。

Landisman等[1]提出了在时间域采用矩形窗作为时间窗口的移动窗分析法, Dziewonski等[2]提出了在频率域采用高斯滤波器的多重滤波法。如果将移动窗分析法中的矩形窗改为高斯窗,那么时间域移动窗分析法与频率域多重滤波法是等价的。目前,多重滤波法作为最常用的提取群速度的方法,其效果在很大程度上取决于高斯滤波参数α,因此需要选择合适的高斯滤波参数值,前人对此作了大量的研究: Inston等[10]提出了最佳带宽滤波; Cara[11]提出了最佳滤波方案; Nyman等[12]提出了均等显示方法; Herrmann等[13]给出了不同震中距的高斯滤波参数的参考取值; Kolínsky[14]研究发现,高斯滤波参数与信号周期之间存在准线性变化的规律,但仅适用于该研究中所采用的天然地震数据;朱良保等[15]提出了线性时间分辨方法选择高斯滤波参数;陈浩朋等[16]提出了不同震中距的高斯滤波参数按照周期分段进行取值。本文将采用Dziewonski等[2]、Herrmann等[13]、陈浩朋等[16]分别提出的高斯滤波参数α取值,并且在陈浩朋等[16]的周期分段取值基础上作了调整改进,利用多重滤波法对合成瑞利面波数据和高质量实际数据进行群速度的提取,分析高斯滤波参数α的不同取值对多重滤波法的影响。

1 多重滤波法原理

1.1 单台法

中心频率为ωn的高斯带通滤波器Hn(ω)为

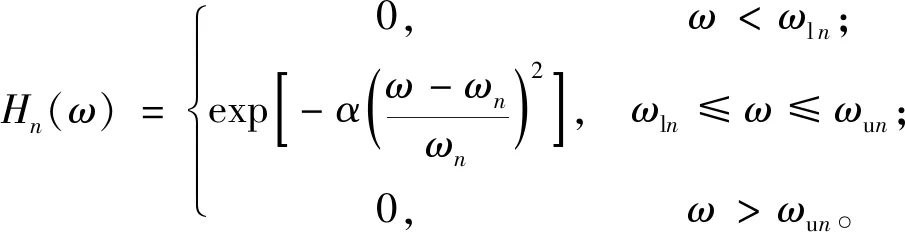
(1)

其中:α为高斯滤波参数;ωn为中心频率;ωln为中心频率的下限频率;ωun为中心频率的上限频率[2-3,16-17]。

令BAND=(ωun-ωn)/ωn=(ωn-ωln)/ωn,β=αBAND2。 其中BAND为相对带宽,β为截断阈值。 实际计算中必须对高斯函数进行截断, 原则上在截断后不能引起明显的吉普斯效应,β一般取值为3,截断处的能量相对于能量峰值下降了30 DB。当高斯滤波参数为常数时,BAND也为常数时,此时称为常相对带宽[15]。

设某一台站记录的天然地震面波数据为f(t), 对f(t)进行傅里叶变换得到f(ω); 在频率域, 用中心频率为ωn的高斯带通滤波器Hn(ω)对f(ω)进行滤波得到Fn(ω); 然后将Fn(ω)进行傅里叶反变换转换到时间域, 并对其进行希尔伯特变换得到幅值包络, 最大振幅的到时即为该频率ωn的群速度波包的到时tn; 假设面波沿大圆路径传播, 根据震中距L和群速度波包到时tn, 即可计算出该中心频率ωn的群速度Un=L/tn。 重复上述步骤, 直到求出所有待求频率(周期)的群速度值[17]。

1.2 双台法

假设面波沿大圆路径,当两个台站与震中近似在同一条大圆弧上时(图1),可以用双台法提取两个台站间的群速度。

设这两个台站记录的天然地震面波数据分别为f1(t)、f2(t),其互相关函数f(t)为

(2)

图1 双台法示意图Fig.1 Diagram for two-station method

f(t)相当于第1个台站激发第2个台站接收的地震记录。 此时, 用单台法的步骤提取f(t)的群速度[16]。

单台法和双台法只是面波的数据来源不同,单台法适用于震中在研究区域内,双台法适用于震中在研究区域外。在提取群速度的原理和步骤上,单台法和双台法没有区别,故而本文均以单台法为例。

2 高斯滤波参数

2.1 理论瑞利面波数据

为了分析高斯滤波参数α的取值对多重滤波法的影响,采用模态叠加方法[13]计算理论瑞利面波数据:选择地球速度结构AK135模型[18],地震震源参数见表1,5个接收台站,其震中距分别为1 000、2 000、3 000、4 000和8 000 km,方位角45°,数据采样间隔为1 s。震中距为3 000 km的理论瑞利面波数据及其振幅谱见图2,提取的周期范围为4～220 s。

2.2 高斯滤波参数取值

在多重滤波法中,选择合适的高斯滤波参数α可以减少面波群速度测量误差。

表1 地震震源参数

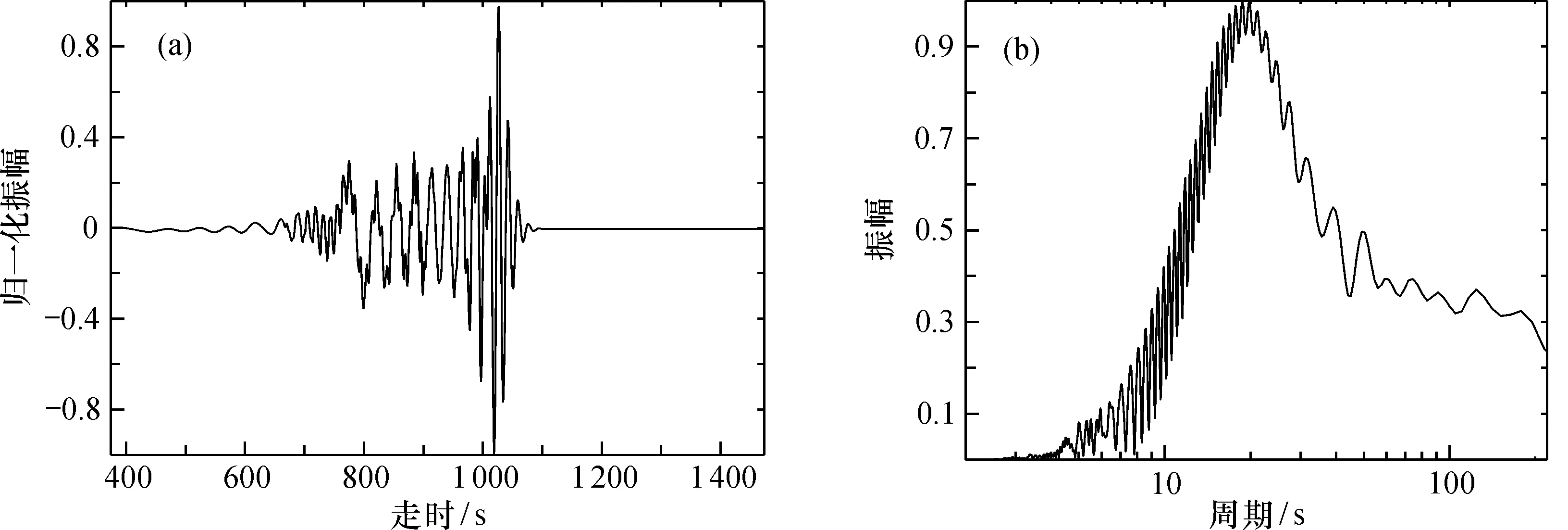
图2 震中距3 000 km的理论瑞利面波数据(a)及其振幅谱(b)Fig.2 Synthetic seismogram of Rayleigh wave at distance of 3 000 km(a) and its amplitude spectra(b)

Dziewonski等[2]给出了α=50.3;Herrmann等[13]给出了4～100 s内不同震中距下高斯滤波参数α的参考值(表2,文献[13]并没有明确给出震中距3 000 km时的高斯滤波参数α参考值, 但可以根据震中距2 000 km和4 000 km的α参考值插值求取)。 采用上述两种不同的常相对带宽取值方案, 对不同震中距的理论瑞利面波数据进行多重滤波, 其结果分别见图3a1—a5、 图3b1—b5。 采用Dziewonski等[2]、Herrmann等[13]的高斯滤波参数α取值提取的群速度曲线在周期较大时均出现起伏,与理论群速度曲线拟合程度差;并且震中距越小,群速度曲线在周期较大时的起伏越剧烈,与理论群速度曲线拟合程度越差。这说明,高斯滤波参数α的选取若只考虑震中距的大小,在周期较大时很难取得较好的效果,因此,当周期范围跨度较大时,高斯滤波参数α取值不仅应考虑震中距,还应考虑周期。

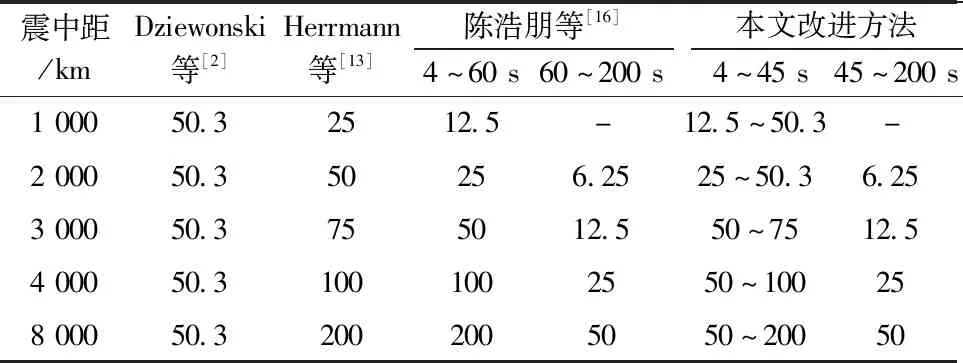
表2 不同方法的高斯滤波参数α取值

陈浩朋等[16]给出了不同震中距不同周期分段的高斯滤波参数α取值(表2),对不同震中距的理论瑞利面波数据进行多重滤波,其结果见图3(c1—c5)。 除了震中距1 000 km以外,采用陈浩朋等[16]的高斯滤波参数α取值提取的群速度曲线在周期较大时没有出现明显的起伏,且与理论群速度曲线拟合较好,这是因为陈浩朋等[16]的高斯滤波参数α取值同时考虑了震中距和周期范围。

但当震中距为2 000、3 000、4 000和8 000 km时,尤其是当震中距为2 000、3 000 km时,采用陈浩朋等[16]的高斯滤波参数α取值提取的群速度曲线在45～60 s范围内与理论群速度曲线拟合相对较差,这说明陈浩朋等[16]的周期分段点60 s,取值过大,经过试验后将周期分段点由60 s调整为45 s(表2), 改进后提取的群速度曲线见图3(d2—d5),改进后提取的群速度曲线在45～60 s范围内与理论群速度曲线拟合得更好。

对于不同震中距,在周期小于45 s范围内,尽管Dziewonski等[2]、Herrmann等[13]、陈浩朋等[16]的高斯滤波参数α取值不同(表2),但提取的群速度曲线均无明显区别(图3a1—a5, b1—b2, c1—c5),这说明在周期小于45 s范围内,高斯滤波参数α取值范围较大,不应局限于某一数值,改进后的取值范围见表2。

另外,当震中距为1 000 km,即震中距较小时,在周期大于45 s范围内,采取不同的高斯滤波参数α取值提取的群速度曲线均与理论群速度曲线拟合差(图3a1,b1,c1), 这说明提取的周期不应超过45 s(表2)。

3 实际数据

本文使用南岭西部地区流动台站观测数据作为试验数据, 地震事件信息见表3, 共12个台站(表4), 台站的地震记录见图4, 地震记录质量高。 以JH01台站记录为例, 采用4种不同高斯滤波参数α取值方案(表2)对其进行多重滤波, 结果如图5所示。

采用Dziewonski等、 Herrmann等给出的常相对带宽取值提取的群速度曲线在周期45 s后均出现一定程度的起伏; 采用陈浩朋等给出的周期分段α取值提取的群速度曲线在60 s后起伏消失, 但在45～60 s范围内仍有一定程度的起伏; 采用改进后的周期分段α取值提取的群速曲线在45～60 s范围内起伏也消失。 由此可见, 高斯滤波参数α取值失当会造成多重滤波法提取的群速度曲线在周期大于45 s范围内出现假象起伏, 这在一定程度上会影响后续的速度反演精度。 对12个台站提取的群速度曲线取平均值(图6), 在4种不同的α取值方案中, 改进后的周期分段α取值提取的平均群速度曲线最光滑。

表3 地震事件信息

表4 宽频带流动台站信息

图4 地震事件不同台站垂直分量记录Fig.4 Vertical components record of different stations for the same earthquake event

图5 对JH01台站记录采用不同α取值提取的群速度频散Fig.5 Group-velocity measurements record of JH01 station by MFT using different α values

4 结论与建议

采用Dziewonski等、Herrmann等的常相对带宽取值、陈浩朋等的周期分段取值、改进的周期分段取值,分别对不同震中距的理论瑞利面波数据和高质量的实际数据进行多重滤波,并对这4种不同α取值方案的提取结果进行对比,结果表明:

(1)当震中距为1 000 km时,即震中距较小时,提取的周期不应超过45 s。

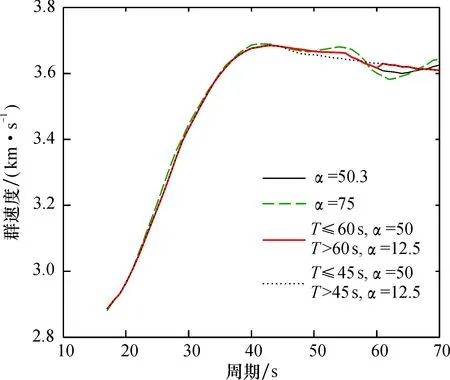
图6 采用不同α取值提取的所有台站的平均群速度频散Fig.6 Average group-velocity measurements of all stations by MFT using different α values

(2)当周期范围跨度较大时,高斯滤波参数α取值不仅应考虑震中距,而且还应考虑周期。

(3)对于不同震中距:在周期小于45 s时,不同的高斯滤波参数α取值对群速度的提取无明显影响,此时α取值范围较大,不应局限于某一数值;但在周期大于45 s时,不同的高斯滤波参数α取值对群速度的提取影响较大,此时α的取值应谨慎。

(4)在周期大于45 s时,采用Dziewonski等、Herrmann等的常相对带宽取值提取的群速度频散曲线有明显的起伏;采用陈浩朋等提出的周期分段α取值提取的群速度曲线虽然避免了周期大于60 s后的假象起伏,但在45～60 s范围内仍有一定程度的假象起伏;将陈浩朋等的周期分段点60 s调整为45 s后,避免了45～60 s范围内的假象起伏。因此,在4种不同的α取值方案中,本文改进后的周期分段α取值效果最好。