桩后及桩侧土拱共同作用的抗滑桩桩间距分析

邱子义,韩同春,豆红强,李智宁

( 浙江大学 滨海与城市岩土工程研究中心,浙江 杭州 310058；浙江大学 软弱土与环境土工教育部重点实验室,浙江 杭州 310058)



桩后及桩侧土拱共同作用的抗滑桩桩间距分析

邱子义,韩同春,豆红强,李智宁

( 浙江大学 滨海与城市岩土工程研究中心,浙江 杭州 310058；浙江大学 软弱土与环境土工教育部重点实验室,浙江 杭州 310058)

摘要:为得到较为符合工程实际的抗滑桩合理桩间距计算公式,在考虑桩土相互作用及已有数值模拟结果的基础上,提出桩后土拱及桩侧土拱同时存在并共同受力的计算模型,且两者拱轴线线型符合合理拱轴线条件.分析抗滑桩桩后土拱及桩侧土拱极限承载力,并假定在合理桩间距条件下,桩后土拱及桩侧土承载力之和为土体总推力的大小.在此假设的基础上,推导出合理桩间距的计算公式,分析考虑滑坡推力在沿桩深度方向上非均匀分布的工况,并与工程实际进行比较,结果与之相符合.对所得合理桩间距计算公式中参数进行分析,结果表明：合理桩间距随抗滑桩截面尺寸及土体黏聚力增大而线性增加,随土体内摩擦角增加而曲线递增.

关键词：滑坡治理； 抗滑桩； 土拱效应； 合理桩间距

土拱效应广泛存在于岩土工程中,其实质是土体的不均匀变形引起的应力转移现象,即将土体受到的推力转移到支挡结构上.Terzaghi[1]在活动门试验中验证了土体中土拱效应的存在.Liang等[2-3]对抗滑桩中土拱效应的产生机理进行了详细分析,Li等[4]在二维条件下,利用数值模拟的方法对抗滑桩间土拱的形成及发展进行了说明.李忠诚等[5-6]利用数值模拟的方法对三维条件下,影响抗滑桩土拱效应的主要因素进行了系统分析.戴自航等[7]在考虑桩土间相互作用的情况下,结合实际工程,利用三维数值模型分析了滑坡安全系数与抗滑桩设计参数的关系.Lirer[8]结合滑坡现场的长期监测试验及三维数值模拟,分析了抗滑桩与滑坡土体相互作用的关系.

实际工程中,抗滑桩的加固机理即利用土拱效应,将滑坡的下滑力传递到抗滑桩上,从而达到治理滑坡的目的.因此,充分考虑抗滑桩的成拱情况对于经济合理的确定桩间距具有重要意义.周德培等[9]在考虑桩后土拱承载力条件下,利用静力平衡条件及土拱拱顶处、拱脚处破坏准则,推导出了合理桩间距的计算公式.赵明华等[10-12]探讨了滑坡面倾斜的情况下,以桩后土拱为研究对象,推导出了合理桩间距的计算公式；并在考虑桩侧土拱承载力的条件下,利用桩侧摩阻力不小于滑坡推力的条件及拱顶处、拱脚处的强度准则,推导出了合理桩间距的计算公式.李邵军等[13]在基于桩土相互作用的机制分析上,建立了合理桩间距的计算公式.肖世国等[14]假定桩土间受压区形状为梯形,结合桩土间变形协调条件,得出了合理桩间距的计算公式.

上述对于合理桩间距的研究在特定条件下有其适用性,但均仅考虑了桩后土拱或桩侧土拱单独作用的情况,在进行算例验证时,亦假设抗滑桩后推力沿深度方向均匀分布,而实际上滑坡推力沿桩身的分布情况随滑坡体的性质呈现出多种分布形式[15-17].目前数值模拟的结果表明，桩侧土拱和桩后土拱同时存在[3,4,13].林治平等[18]详细分析了桩侧土拱和桩后土拱在单独作用及联合作用下的关系,得出两拱联合作用的极限承载力可近似为两者单独作用承载力之和.基于前人的研究成果,本文同时考虑桩后土拱及桩侧土拱存在,推导出合理桩间距的计算公式,并在桩后推力沿深度非均匀分布条件下,验证计算公式.

1计算模型

依照周德培等[9-10]提出的处理方法,将土拱简化为水平拱,并处于平面应变状态.由于在坡体推力下,桩后土拱和桩侧土拱同时存在,基本的分析图如图1所示.其中,a为抗滑桩桩侧面宽度,b为抗滑桩正面宽度,l为抗滑桩间净间距.

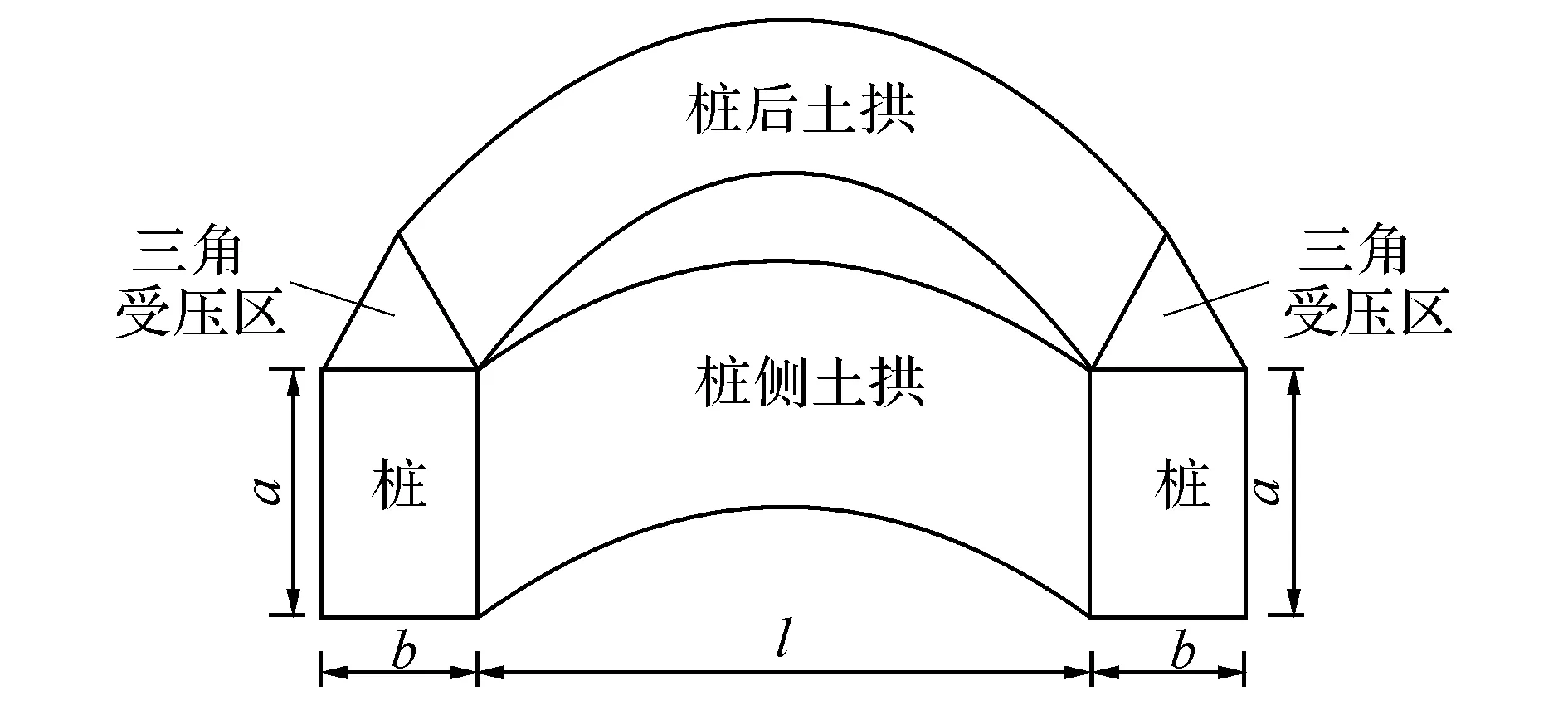
图1　桩后及桩侧土拱效应同时存在示意图Fig.1　Sketch for soil arch behind pile and in pile side

实际工程中抗滑桩的类型主要是矩形桩和圆形桩.由于抗滑桩分析中,圆形截面可采用内接正方形进行等效代换[19],以矩形桩作为分析对象,既能使讨论的问题得到简化,又不失研究结果的一般性.

为使土拱的受力分析得到合理的简化,假定相邻两桩间的土拱曲线符合合理拱轴线方程；土拱后水平土压力沿桩间均匀分布于土拱上,并且土拱厚度保持不变.取单位桩长土拱进行受力分析,简化计算模型图如图2所示.其中,土拱矢高为h,土拱所受均布推力的值为q,Fx及Fy为土拱拱轴线在拱脚或拱顶截面所受到的水平向及竖直向外力.

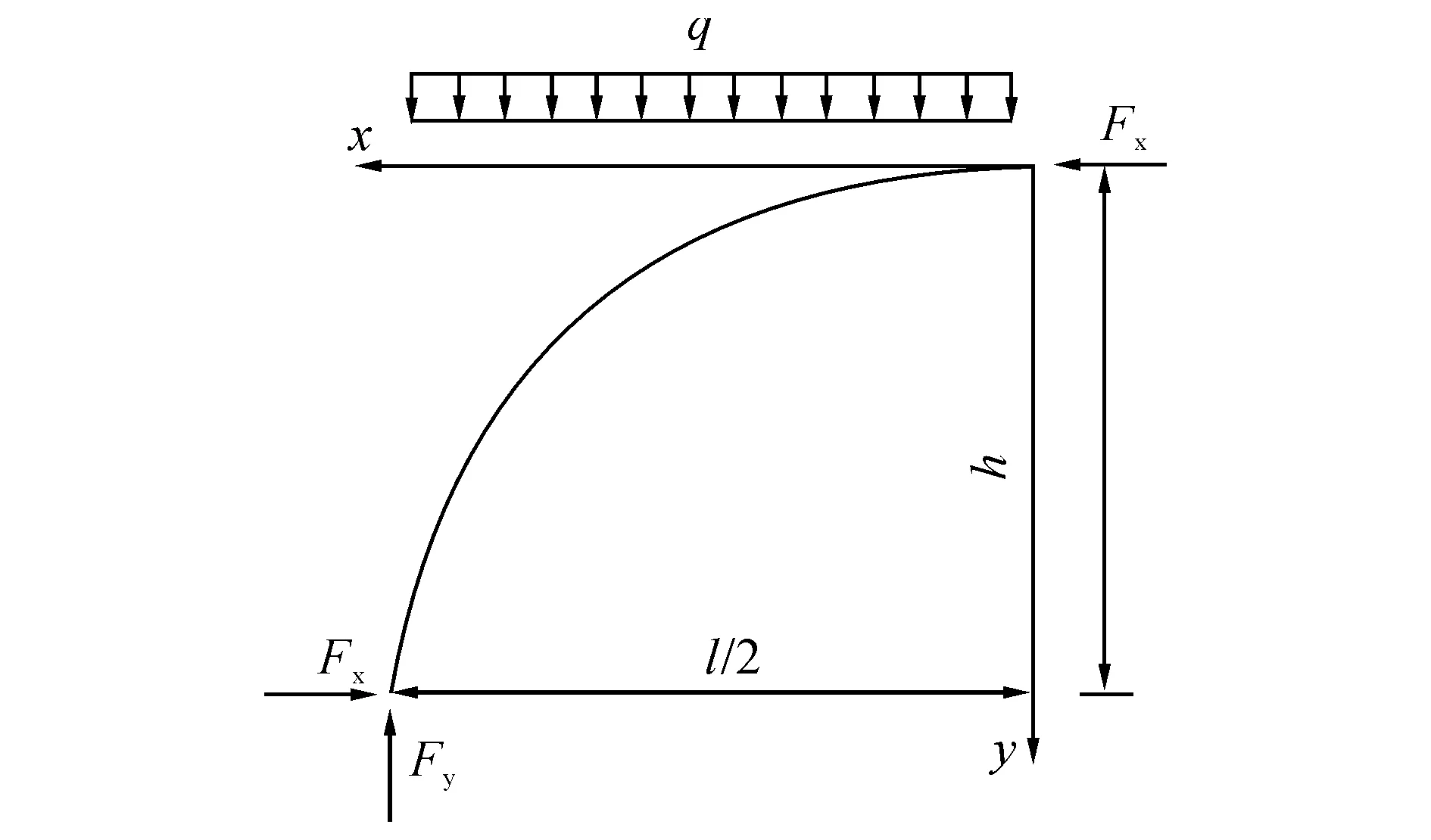
图2　土拱受力分析示意图Fig.2　Force analysis sketch for soil arching

根据图2, 由合理拱轴线在均布推力作用下的力学特点是所有截面均无弯矩和剪力,拱圈沿拱轴线切线方向仅受轴向压力作用.因此土拱曲线方程为

y=4hx2/l2.

(1)

由静力平衡条件可知拱脚处反力

Fx=ql2/(8h),

(2)

Fy=ql/2.

(3)

拱轴线上任意点处所受的正压力大小为

(4)

式中：x为所取截面横坐标.分析式(4)可得,轴向压力FN随x的增大而增大,x=l/2即拱脚处,FN取最大值.在等截面拱圈条件下,压应力亦在拱脚处取最大值,因此,最不利截面位置为拱脚处截面.

由于桩后土拱及桩侧土拱拱轴线均为合理拱轴线,式(1)～(4)对于两者均可使用,在进行相应的计算时,仅须将相应的参数符号调整,公式的形式并不发生变化.

2合理桩间距的确定

2.1基本假定

由于桩发生土拱效应时将同时存在桩后土拱及桩侧土拱,并且根据文献[18],两者共同作用的极限承载力可近似取为两者单独作用时的极限承载力之和.

综合上述分析,作出如下假设：1)在抗滑桩间距为最佳桩间距时,桩后土拱和桩侧土拱同时存在；2)两土拱所受的推力均为匀分布,土拱曲线为合理拱轴线,且两者承载力之和等于桩后总推力；3)按照前人的简化处理方法[9,10,16],桩后土拱受滑坡推力范围近似取为抗滑桩间净间距.

2.2合理桩间距的确定

规定桩侧土拱相关参数的下标均为“1”,桩后土拱相关参数的下标均为“2”.

1)桩侧土拱.

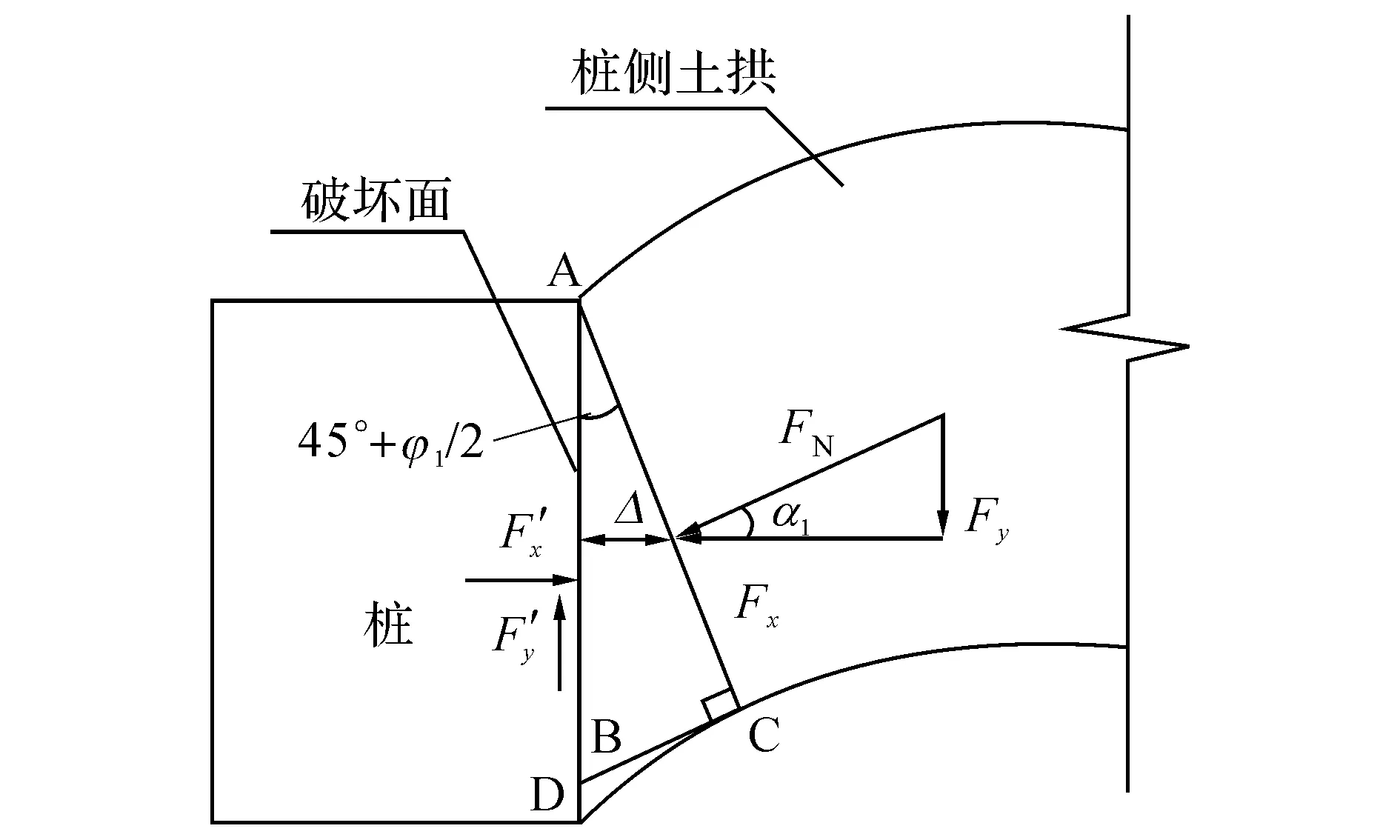
图3　桩身侧面为拱座的土拱Fig.3　Soil arching body supporting by side surface friction of piles

(5)

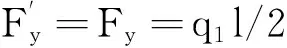
(6)

式中：q1为桩侧土拱所受推力,h1为桩侧土拱矢高.在破坏面上根据摩尔-库伦强度准则

(7)

式中：c1为桩土间黏聚力.桩侧为岩石或岩块时取φ1=φ/2,为细粒土时取φ1=φ/2或φ1=2φ/3；可取c1=ctanφ1/tanφ[12],q1为桩侧土拱所受推力大小,c、φ为土体的抗剪强度指标(黏聚力和内摩擦角).将式(5)、(6)代入(7)可得

(8)

由极限平衡理论,大主应力作用面与破裂面的夹角为(45+φ1/2)[20],因此有

(9)

桩侧土拱厚度t1为

(10)

式中：lAB为图3中AB段长度.联立式(8)、 (9)可得桩侧土拱极限承载力表达式为

(11)

(2)桩后土拱.

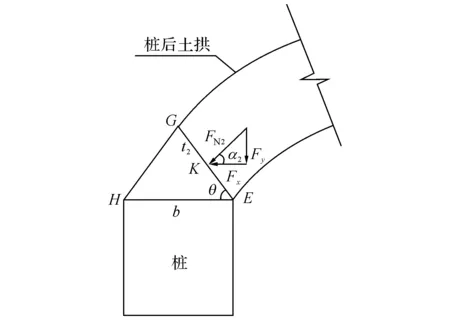
图4　两侧土拱交汇处的三角形受压区Fig.4　Triangular compressive zone in intersectional region of adjacent soil arch

对桩后土拱,如图4所示,相邻两土拱在此形成三角形受压区.其中,面EG为拱脚截面,点K为拱轴线与拱脚截面交点,FN2为作用在拱脚截面上的压力,α2为拱脚处拱轴切线与水平方向夹角,t2为桩后土拱拱厚,根据文献[21]及[22],在点K,土体沿水平方向发生剪切破坏,由极限平衡理论可得

α2=45°-φ/2,

因此

(12)

式中：h2为桩后土拱矢高.如图4所示,由几何条件可知θ=45°+φ/2.对拱脚截面点K,为单向受压状态,由单向受压下摩尔-库伦强度准则可得

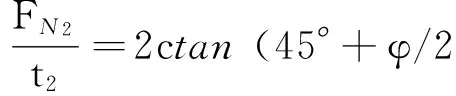
(13)

(14)

由前文可知

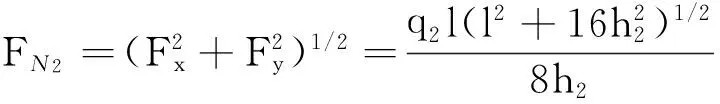
(15)

将式(14) 、(15)代入式(13)得

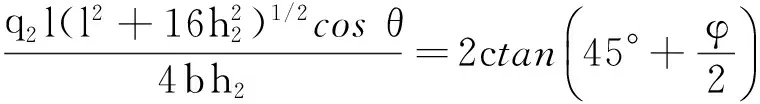
(16)

联立式(12) 、(16)有

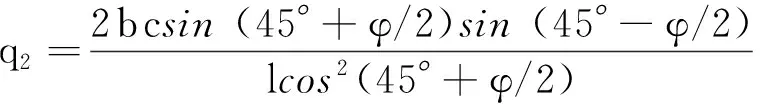
(17)

式(17)为桩后土拱极限承载力计算表达式.

综合上述对桩后土拱及桩侧土拱受力分析,根据两土拱所受推力之和为桩后总推力可得

q1+q2=q.

(18)

将式(11) 、(17)代入式(18)可得

(19)

整理式(19)可得合理桩间距的计算式:

(20)

土拱效应的产生机理在于土体间的“楔紧”过程.由于桩后土拱处土体受到抗滑桩的直接阻挡,使得“楔紧”过程较为容易发生,在抗滑桩间有土拱效应产生时，桩后土拱一般均存在桩后土拱亦一般存在.桩侧土拱处土体受抗滑桩的阻挡主要来自于桩侧摩阻力,相对于抗滑桩直接阻挡所引起的土体位移减小量要小,因此桩侧土拱稳定存在需要桩前存在土体,并提供一定的被动土压力.本文提出的计算方法对于抗滑桩前为临空面的工程(如基坑支护)不适用.另外,根据文献[15],当滑坡推力为矩形分布时,滑坡体为岩石,此时抗滑桩间产生“岩拱效应”,岩拱中存在较大的剪力和弯矩,计算时不可忽略[23].对此种情况,本文算法亦不适用.

3算例分析

3.1考虑滑坡推力非均匀分布

由于抗滑桩后滑坡推力大小在沿桩深度方向呈多种分布形式,应结合土拱破坏强度条件,得出最不利受力处所在的深度位置.

对桩侧土拱,由式(4)、(10)可得土拱截面正应力σ1为

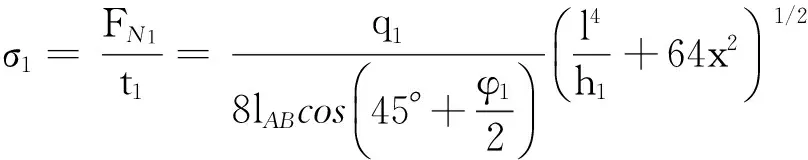
(21)

从式(9)分析可得,桩侧土拱矢高h1在桩间距l确定的情况下为定值,lAB在拱脚处拱轴线切线与水平方向夹角α1确定的情况下为定值.根据式(9),在土体内摩擦角确定情况下为定值,因此lAB不随深度变化而变化.在计算抗滑桩后滑坡推力分布情况时,根据滑坡体性质的不同可简化为三角形、矩形、梯形和折线形(类抛物线形)4种[16].如图5所示,上述4种分布形式中,滑坡推力均在滑裂面处取最大值.根据式(21),a、x、l的取值与深度无关,而当q1增大时,桩侧土拱截面正应力σ1增大,在桩悬臂根处σ1取最大值,为最不利受力情况.因此，对桩侧土拱,应取悬臂根处的相应参数确定合理桩间距.

对桩后土拱,由式(14)、(15)可得土拱截面正应力为

(22)

式(22)与式(21)结构类似,其中θ仅与φ相关,与深度无关.从式(12)分析可得,桩后土拱矢高h2在桩间距确定的情况下为定值.式(22)与(21)的分析过程相同,本文不再赘述.对桩后土拱,亦应取悬臂根处的相应参数确定合理桩间距.综合两者的分析结果,在计算合理桩间距时,应取悬臂根处的相应参数进行计算.

图5　滑坡推力分布形式Fig.5　Distribution type of landslide-thrust

3.2算例

算例引自文献[10],紫阳滑坡位于汉江北岸一级阶地上,自然地面倾向汉江.滑坡体倾斜角为20°,主要属全新系堆积物, 以黏土和粉质黏土为主,夹杂有碎石.东、西两滑坡体组成滑动区,江岸基岩出露边界处为两者剪出口.下伏基岩为强风化深度为3～5m的千枚岩,表面倾向汉江,并与其上第四系地层形成角度不整合接触.滑坡体上部已形成滑动面,下部将沿基岩滑动.根据室内试验,接触面上强度指标如下：c=130kPa,φ=15°,桩截面尺寸为正面宽度b=2m,侧面宽度a=3m,桩受荷段长度L=10.5m,桩后单位宽度所受滑坡推力为1 076.6kPa.

滑坡推力水平分量大小为1 076.6×cos20°=1 011.7kPa.由于滑坡土体以黏土及粉质黏土为主,参照[15]及文献[16],桩后滑坡推力的分布形式可取为三角形分布.当滑坡推力为三角形分布时,在桩悬臂根处有

式中：Fh为桩后滑坡推力水平分量,z为桩身悬臂根处距地表的深度大小，此处其大小即为L.滑坡土体以黏土和粉质黏土为主,属细粒土,故桩土间摩擦角φ1取

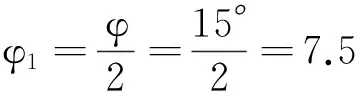
桩土间黏聚力

将所得的参数代入式(20)可得,滑坡推力为三角形分布时,合理桩间净间距为5.76m,较为符合工程实际.

对本文算例,在考虑土拱效应三维现象的前提下,取滑坡推力形式为三角形分布,利用文献[9-12]及文献[19]中的算法,所得合理桩间距值相应分别为2.45、2.50、2.21、4.35及22.73m. 对比文献中的计算结果与本文计算结果可知,在考虑土拱效应三维分布的情况下,文献[9-12]中的算法计算结果偏保守,而文献[19]的计算结果偏大.因此,本文提出的计算方法具有一定的实用价值.

3.3桩间距影响参数分析

分析式(20)可知,抗滑桩的最佳桩间距(净间距)的值与土体强度指标c、φ值、桩土间的摩擦角φ1,桩土间黏聚力c1,桩后土拱受到的总推力q及桩自身的尺寸a、b有关.总推力q在设计之前就已经确定,可视为常量.并且,对于特定的工程,桩土间的c1、φ1值可根据土体的c、φ值换算得到.因此,本文仅探讨l与c、φ、a、b的关系.

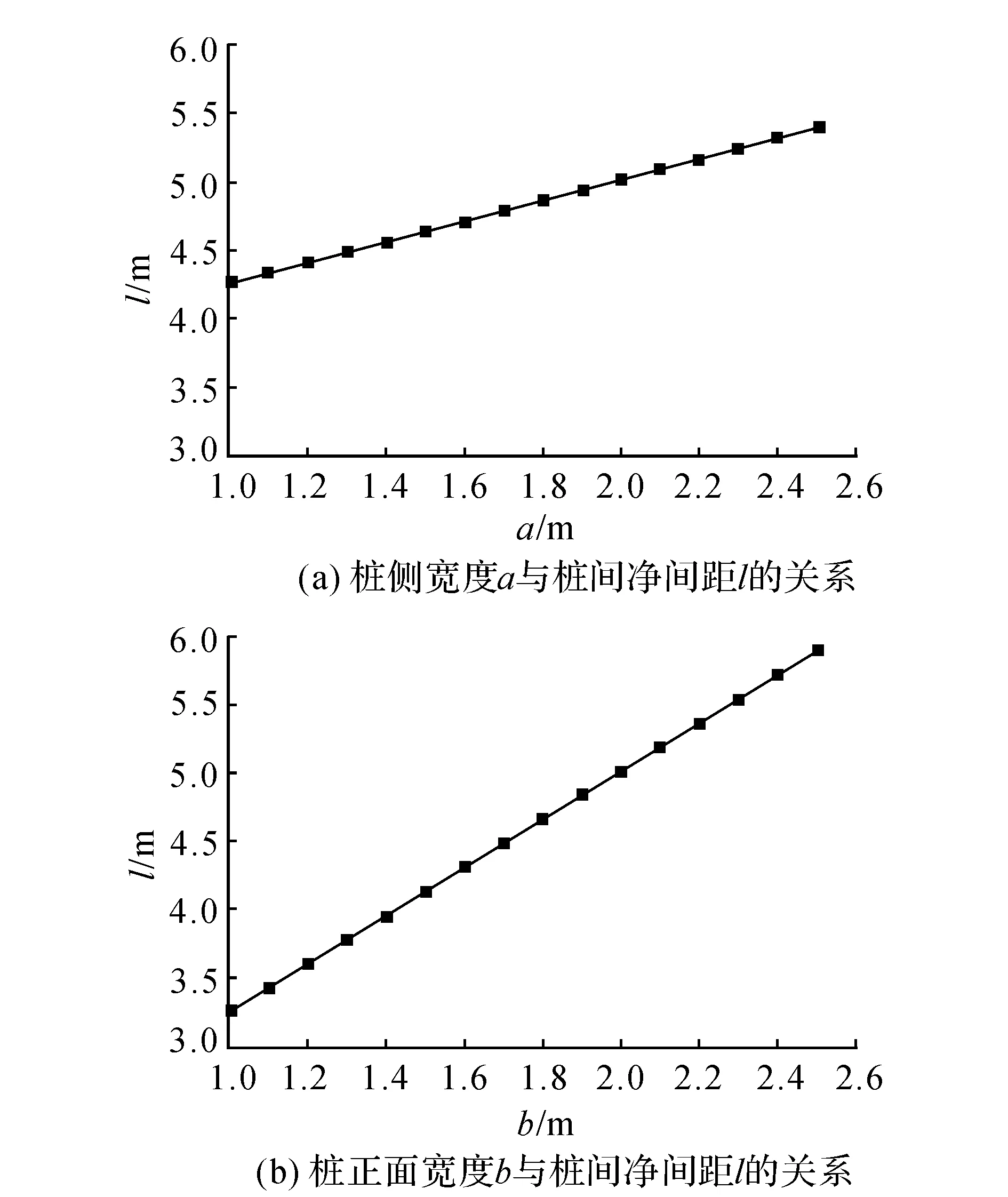
图6　桩横截面尺寸与桩间净间距关系图Fig.6　Relationship between pile cross section and pile spacing

图6表示a与l、b与l的关系.其中,在采集图6的数据时,取b=2.0m,a取值在1.0～2.5m变动,其余参数的取值同算例.取a=2.0m,b取值在1.0～2.5m变动,其余参数取值同算例.从图中可知,桩间距l随着a、b的增大而增大,但a和b在相同增幅下,l的增幅并不相同,l对桩正面宽度b的变化更为敏感.产生这种现象的原因是：在桩后土拱和桩侧土拱共同作用情况下,根据文献[4]及[18]的数值模拟结果,桩后土拱分担的滑坡推力大于桩侧土拱,占主导地位.根据式(17)可知，桩后土拱的极限承载力与桩正面宽度b的取值有关，因此l对b的变化更为敏感.

图7表示土体强度指标c、φ与l的关系.其中,采集图7数据时,为使φ与l的关系能更加直观地表现出,φ的取值变动范围不可过小,因此将φ的取值上限取为60°.从图中可以得出,l随c、φ的增加而增加,但增加的趋势并不相同.l随c仅是简单的线性增加关系,而随φ增加的趋势呈曲线递增,l对φ的敏感性高于l对c的敏感性.分析其原因是：φ的变化将引起φ1、c1值的变化,而c的变化仅引起c1的变化；并且,从式(20)分析可知,l与c间的函数关系较为简单,而与φ间的函数关系较为复杂,相应的敏感度也将更高.

图7　土体强度指标与桩间净间距关系图Fig.7　Relationship between soil strength indicators and pile spacing

4结论

(1)合理桩间距大小l与抗滑桩截面尺寸a、b及土体黏聚力c呈线性关系,与土体内摩擦角φ呈曲线递增关系.并且l对b的敏感程度大于a.滑坡土体的强度指标为抗滑桩合理桩间距大小的决定因素.

(2)对于某一确定的工程,土体强度指标一般为确定值,不随设计的变化而变.桩截面尺寸，特别是桩正面宽度b及相邻抗滑桩桩间距l,是工程设计中需考虑的重要因素.

(3)实际工程中,可将计算结果取一定的安全系数来确保设计的安全性.为得到更加精确的合理桩间距取值,应利用试验或是数值模拟等方式,对桩后土拱及桩侧土拱间的相互作用关系作进一步探索.

参考文献(References):

[1]TERZAGHI.Theoreticalsoilmechanics[M].NewYork:JohnWileyandSons, 1943．

[2]LIANGR,ZENGS.Numericalstudyofsoilarchingmechanismindrilledshaftsforslopestabilization[J].SoilandFoundation, 2002, 42(2) : 83-92．

[3]CHENCY,MARTINGR.Soil-structureinteractionforlandslidestabilizingpiles[J].ComputersandGeotechnics, 2002, 29(5): 363-386．

[4]LICD,TANGHM,HUXL,etal.Numericalmodellingstudyoftheloadsharinglawofanti-slidingpilesbasedonthesoilarchingeffectforErlibanlandslide,China[J].KSCEJournalofCivilEngineering, 2013, 17(6): 1251-1262．

[5] 李忠诚, 杨敏. 被动受荷桩成拱效应及三维数值分析[J]. 土木工程学报, 2006, 39(3): 114-117．

LIZhong-cheng,YANGMin,Soilarchingeffectonpassivepilesand3-Dnumericalanalysis[J].ChinaCivilEngineeringJournal, 2006, 39(3): 114-117．

[6] 刘钦, 李地元, 刘志祥, 等. 水平推力作用下抗滑桩间土拱效应影响因素的数值分析[J]. 中南大学学报：自然科学版, 2011, 42(7): 2071-2077．

LIUQin,LIDi-yuan,LIUZhi-xiang,etal.Numericalanalysisofinfluencefactorsonsoilarchingeffectbetweenanti-slidingpilesunderhorizontalpushingloads[J].JournalofCentralSouthUniversity:ScienceandTechnology, 2011, 42(7): 2071-2077．

[7] 戴自航, 徐祥. 边坡抗滑桩设计计算的三维有限元法[J]. 岩石力学与工程学报, 2012, 31(12): 2572-2578．

DAIZi-hang,XUXiang. 3Dfiniteelementmethodfordesigncomputationsofanti-slidepiles[J].ChineseJournalofRockMechanicsandEngineering, 2012, 31(12): 2572-2578．

[8]LIRERS.Landslidestabilizingpiles:Experimentalevidencesandnumericalinterpretation[J].EngineeringGeology, 2012, 149: 70-77．

[9] 周德培, 肖世国, 夏雄. 边坡工程中抗滑桩合理桩间距的探讨[J]. 岩土工程学报, 2004, 26(1): 132-135．

ZHOUDE-pei,XIAOShi-guo,XIAXiong.Discussiononrationalspacingbetweenadjacentanti-slidepilesinsomecuttingslopeprojects[J].ChineseJournalofGeotechnicalEngineering, 2004, 26(1): 132-135．[10] 赵明华, 廖彬彬, 刘思思. 基于拱效应的边坡抗滑桩桩间距计算[J]. 岩土力学, 2010, 31(4): 1212-1216．

ZHAOMing-hua,LIAOBin-bin,LIUSi-si.Calculationofanti-slidepilesspacingbasedonsoilarchingeffect[J].RockandSoilMechanics, 2010, 31(4): 1212-1216．[11] 赵明华, 陈炳初, 刘建华. 考虑土拱效应的抗滑桩合理桩间距分析[J]. 中南公路工程, 2006, 31(2): 1-3．

ZHAOMing-hua,CHENBing-chu,LIUJian-hua.Analysisofthespacingbetweenanti-slidepilesconsideringsoil-archeffect[J].CentralSouthHighwayEngineering, 2006, 31(2): 1-3．[12] 胡晓军, 王建国. 边坡加固工程中抗滑桩间距的确定[J]. 河海大学学报:自然科学版, 2007, 35(3): 330-333．

HUXiao-jun,WANGJian-guo.Determinationofanti-slidepilespacinginsideslopeconsolidationprojects[J].JournalofHohaiUniversity:NaturalSciences, 2007, 35(3): 330-333．

[13] 李邵军, 陈静, 练操. 边坡桩-土相互作用的土拱力学模型与桩间距问题[J]. 岩土力学, 2010, 31(5): 1352-1358．

LIShao-jun,CHENJing,LIANCao.Mechanicalmodelofsoilarchforinteractionofpilesandslopeandproblemofpilespacing[J].RockandSoilMechanics, 2010, 31(5): 1352-1358．

[14] 肖世国, 程富强. 再论悬臂式抗滑桩合理桩间距的计算方法[J]. 岩土力学, 2015, 36(1): 111-116．

XIAOShi-guo,CHENGFu-qiang.Furtherdiscussiononcalculationmethodofrationalspacingbetweentwoadjacentcantileverpilesforstabilizingslope[J].RockandSoilMechanics, 2015, 36(1): 111-116．[15] 戴自航. 抗滑桩滑坡推力和桩前滑体抗力分布规律的研究[J]. 岩石力学与工程学报, 2002, 21(4): 517-521．

DAIZi-hangStudyondistributionlawsoflandslide-thrustandresistanceofslidingmassactingonantislidepiles[J].ChineseJournalofRockMechanicsandEngineering, 2002, 21(4):517-521．

[16] 张永兴, 董捷, 文海家, 等.考虑自重应力的悬臂式抗滑桩三维土拱效应及合理间距研究[J]. 中国公路学报, 2009, 22(2):18-25．

ZHANGYong-xing,DONGJie,WENHai-jia,etal.Researchonthree-dimensionalsoilarchingeffectandappropriatespacingofcantileveranti-slidepileswithconsiderationofgeostaticstress[J].ChinaJournalofHighwayandTransport, 2009,22(2):18-25．

[17] 刘永莉, 孙红月, 于洋, 等. 基于BOTDR监测技术抗滑桩上滑坡推力确定[J]. 浙江大学学报：工学版, 2012, 46(5): 798-803．

LIUYong-li,SUNHong-yue,YUYang,etal.Determininglandslidethrustonanti-slidingpilebyBOTDRmonitoringtechnology[J].JournalofZhejiangUniversity:EngineeringScience, 2012, 46(5): 798-803．

[18] 林治平, 刘祚秋, 商秋婷. 抗滑桩结构土拱的分拆与联合研究[J]. 岩土力学, 2012, 33(10): 3109-3114．

LINZhi-ping,LIUZuo-qiu,SHANGQiu-ting.Researchonsoilarchofanti-slidepilestructurewithmethodsofseparationandcombination[J].RockandSoilMechanics, 2012, 33(10): 3109-3114．

[19] 贾海莉, 王成华, 李江洪. 基于土拱效应的抗滑桩与护壁桩的桩间距分析[J]. 工程地质学报, 2004, 12(1): 98-103．

JIHai-li,WANGCheng-hua,LIJiang-hong.Analysisofpilespacingbetweenanti-slidepilesandpertainingpilesinaccordancewithsoilarchingeffect[J].JournalofEngineeringGeology, 2004, 12(1): 98-103．[20] 杨雪强, 吉小明, 张新涛. 抗滑桩桩间土拱效应及其土拱模式分析[J]. 中国公路学报, 2014, 27(1): 30-37．

YANGXue-qiang,JIXiao-ming,ZHANGXin-tao,Analysisofsoilarchingeffectbetweenanti-slidepilesanddifferentarchbodymodes[J].ChinaJournalofHighwayandTransport, 2014, 27(1): 30-37．

[21] 刘小丽. 新型桩锚结构设计计算理论研究[D]. 成都：西南交通大学,2003．

LIUXiao-li.Studyondesigningandcomputingtheoryofnewpatternpile-anchorstructures[D].Chengdu:South-westJiaotongUniversity, 2003．

[22] 周文权,冷伍明,阮波,等. 考虑桩土相互作用的抗滑桩临界桩间距研究[J]. 铁道科学与工程学报, 2014,11(3):83-87．

ZHOUWen-quan,LENGWu-ming,RUANBo,etal.Researchofcriticalpilespacingofanti-slidepileconsideringtheinteractionofpileandsoil[J].JournalofRailwayScienceandEngineering, 2014,11(3):83-87．[23] 张骞, 李术才, 张乾青, 等. 抗滑桩岩拱效应与合理桩间距分析[J]. 岩土工程学报, 2014, 36(增2): 180-185．

ZHANGQian,LIShu-cai,ZHANGQian-qing,etal.Analysisonrock-archeffectofanti-slidepilesandrationalpilespacinginengineeringproject[J].ChineseJournalofGeotechnicalEngineering, 2014, 36(Suppl. 2): 180-185．

DOI:10.3785/j.issn.1008-973X.2016.03.021

收稿日期：2015-01-20.

基金项目：国家自然科学基金资助项目(51178423);浙江省自然科学基金资助项目(LY15E080010).

作者简介：邱子义(1990-)，男，硕士生，从事边坡加固等方面的数值及理论研究. ORCID：0000-0003-0445-2955. E-mail：qiuziyi1012@zju.edu.cn 通信联系人：韩同春，男，博士，副教授. ORCID：0000-0001-6553-6795. E-mail：htc@zju.edu.cn

中图分类号：TU 473

文献标志码：A

文章编号：1008-973X(2016)03-07-0559

Analysisofspacingbetweenanti-slidepilesconsideringsoilarchonlateralsidesandback

QIUZi-yi,HANTong-chun,DOUHong-qiang,LIZhi-ning

(Research Center of Coastal and Urban Geotechnical Engineering, Zhejiang University, Hangzhou 310058, China; Key Laboratory of Soft Soils and Geoenvironmental Engineering, Ministry of Education, Zhejiang University, Hangzhou 310058, China)

Abstract:A calculation model considering soil arching behind the pile and soil arching in the pile side working together was established on the basis of numerical simulations by previous studies as well as the interaction between piles and soil, in order to set up a more practical reasonable anti-slide pile spacing calculation formula. The arch axis of soil arching behind the pile and soil arching in the pile side met requirements for the reasonable arch axis. Both the ultimate bearing capacities of soil arch in the pile side and behind the pile were analyzed. With reasonable pile spacing, the summation of both ultimate bearing capacities was equaled to the total load behind the piles. Under this assumption, the formulation was proposed to calculate the reasonable pile spacing. And one case was analyzed according to the non-uniform distribution of landslide thrust along the depth of piles. The calculating results fitted well with engineering practice. At last, some parameters in the formation were analyzed. Results show that the reasonable pile spacing increases linearly with the increase of the section size and cohesion, and increases along the curve with the increase of internal friction angle．

Key words:landslide treatment; anti-slide pile; arching effect; reasonable pile spacing