双压力航空柱塞泵压力切换动态特性

欧阳小平,李　磊,方　旭,杨华勇

(浙江大学 流体动力与机电系统国家重点实验室,杭州 310027)



双压力航空柱塞泵压力切换动态特性

欧阳小平,李磊,方旭,杨华勇

(浙江大学 流体动力与机电系统国家重点实验室,杭州 310027)

摘要:为分析双压力航空柱塞泵压力超调产生的原因从而降低压力超调幅值,建立该泵压力调节机构的动态数学模型,并开展数值仿真研究.分析指出，泵出口等效容腔及斜盘这2个滞后环节是导致泵压力切换时出现压力超调的主要原因.提出降低泵出口等效容腔及在控制柱塞腔前设置阻尼孔等方法来降低压力超调幅值.数值仿真结果表明,当泵出口等效容腔降低为原来的1/3时,泵从高压向低压切换和从低压向高压切换时的压力超调幅值分别下降48.6%和20.4%,设置阻尼孔能有效降低泵从低压向高压切换时的压力超调,但加大了从高压向低压切换时的压力超调幅值,因此应综合运用这些方法来降低压力超调幅值.

关键词：双压力柱塞泵(DPP)；压力切换；压力超调

飞机液压系统一般采用恒压变量泵作为泵源,工作压力根据系统所需要的最高压力设定,实际研究表明,机载液压系统大部分时间工作在设定的恒压压力以下,带来大量能量浪费.双压力/变压力泵源则提供了一种可行的解决方案：当负载需要高压时,泵源工作于恒高压状态；反之则工作于恒低压状态,实质上相当于恒压值不同的变量泵的综合[1].

文献[1]针对双压力柱塞泵压力控制机构在高压段处于临界稳定状态的问题,提出了在调节阀和随动活塞间加一节流短管的方法，但对压力调节压力泵在高低压切换时压力波动过大,但没有提出解决办法.考虑到双压力泵工作在某一恒定压力下,双压力泵动态特性和普通恒压变量泵相同,而这方面已经进行了大量的研究工作,包括带有压力补偿阀的斜盘控制特性分析[4-7]、斜盘控制机构设计[8-9]、斜盘在平衡状态附近的高频振动[10-11]以及变量泵的整体的动态特性研究[12-17].

本文以某型双压力柱塞泵源压力调节机构为研究对象,针对压力切换过程中存在的压力超调的问题,建立双压力泵压力调节机构数学模型,运用数值仿真手段分析压力超调影响因素,提出几种降低压力超调幅值的方法,并讨论这些方法对泵动态特性的影响.

1工作原理

双压力柱塞泵压力控制机构如图1所示,由压力切换电磁阀1、主阀2、卸荷电磁阀3、斜盘控制机构(包括斜盘控制柱塞4及偏置弹簧5)等主要部分组成.在工作过程中,通过控制电磁阀1和3的得失电状态调节泵输出压力至高压、低压及卸荷压力以适应负载压力变化.具体工作原理如下：当电磁阀1和3均处于失电状态时,将泵出口压力ps作用在阀端面积Am上产生的力与弹簧预紧力Fms进行比较,根据比较结果调节阀芯位移,控制斜盘摆角从而实现出口压力恒定,此时泵工作在高压状态；当电磁1得电处于左位时,ps除作用在阀端面积Am上,还作用在阀端面积As, 即将ps(As+Am)与弹簧力Fms进行比较,此时泵工作在低压状态；当电磁阀1失电,电磁阀3得电处于右位时,泵出口压力作用在主阀卸荷推杆无杆侧面积A+、有杆侧面积A-以及阀端面积Am上.弹簧力Fms与ps(A++Am-A-)进行比较,通过设计,确保(A++Am-A-)远大于(As+Am),即可保证泵输出压力保持在一个较低值,即卸荷状态.从以上分析可以看出：双压力柱塞泵在某一恒定压力下工作时与一般恒压变量泵原理相同；而不同恒定压力的调节实际上是通过控制电磁阀来改变主阀阀端等效面积(泵源压力作用在主阀阀芯的实际面积)实现的,当弹簧预紧力不变时,大的阀端等效面积对应于小的泵源恒定压力.

上述调节过程可用图2表示,泵进行高低压切换时,压力先导阀打开或关闭,在极短时间内改变作用在阀端面积As上的作用力Fpv从而改变反馈力Fb,实际上相当于对阀端面积As输入一个阶跃信号[18].反馈力Fb与主阀弹簧预紧力Fms进行比较，得到力偏差信号Fe来调节主阀位移xmv,控制斜盘摆角，改变泵源流量qs,减去负载流量ql和控制油路流量qcm,经泵出口等腔空腔Vd作用后形成出口压力ps.由于斜盘等动态特性的存在,在调节过程中会出现压力超调现象.压力超调大会造成双压力柱塞泵在压力切换过程中出现严重的掉压或超压现象,对系统带来极为不利的影响,本文将围绕图2对某型双压力柱塞泵压力调节机构进行建模,为合理调节其动态特性和降低压力切换过程中的压力超调峰值奠定基础.

图1　双压力泵压力调节机构原理图Fig.1　Schematic diagram of pressure-controlled mechanism for dual-pressure piston pump (DPP)

图2　双压力泵压力调节机构控制框图Fig.2　Control block diagram of pressure-controlled mechanism for DPP

2建模

与主阀相比通流量较小,阀芯行程较短,为分析方便,忽略压力切换电磁阀动态特性,认为压力信号以斜坡形式加载到阀端面积As上.下文将主要对主阀、斜盘摆角控制机构以及出口压力流量转换模块进行建模.

2.1主阀

假设主阀阀芯向右为正方向,如图3所示.忽略瞬态液动力,主阀在运动时主要受到向右的液压力psAm和ppAs(pp为作用在阀端面积As上的瞬态压力,稳态值为ps),向左的稳态液动力kmyxmv、弹簧预紧力Fms、弹性力kmsxmv以及黏性阻尼力,根据力平衡原理可得式(1).

(psAm+ppAs)-Fms=

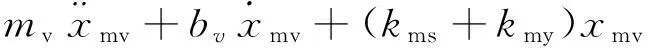
(1)

(2)

式(1)中mv为等效阀芯质量,bv和kmy分别为阀芯运动黏性系数和稳态液动力刚度,kms为主阀的弹簧刚度.kmy由式(2)给出,w(xmv)为阀口面积梯度,pcm为控制柱塞腔压力.

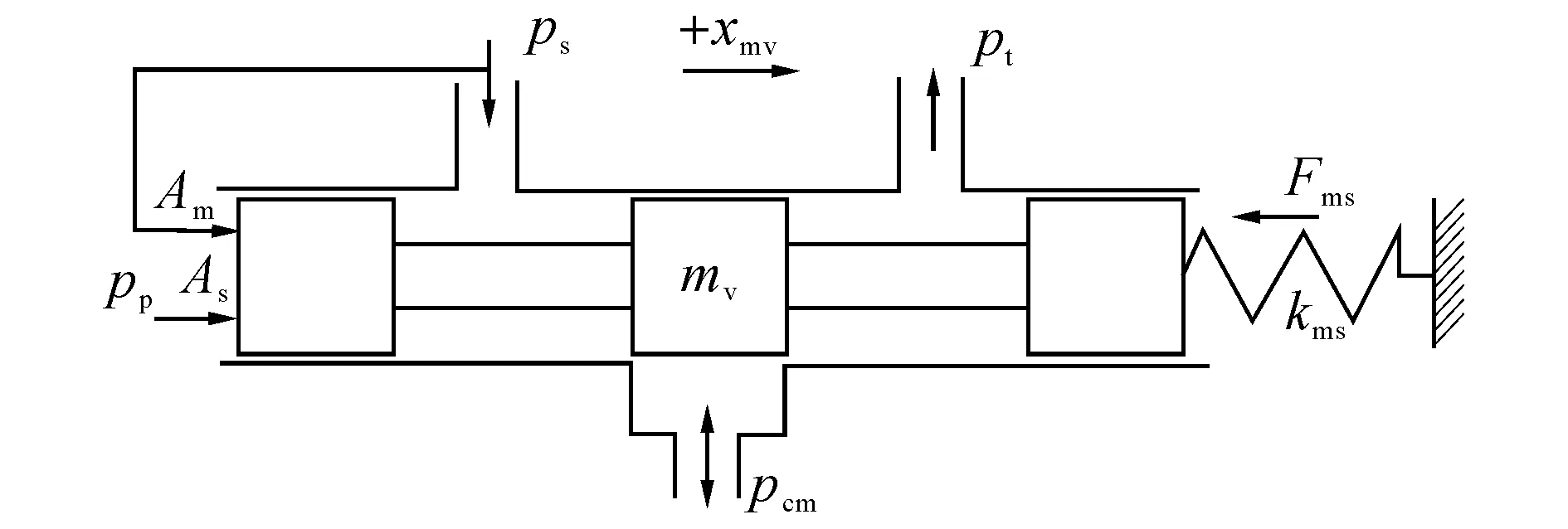
图3　主阀受力示意图Fig.3　Force applied to main valve

2.2斜盘摆角控制机构

如图4所示,斜盘摆角控制机构包括偏置弹簧组件,斜盘以及控制柱塞缸.斜盘受的力矩包括：柱塞腔压力作用在柱塞上并通过滑靴传递至斜盘上的力矩,偏置弹簧对斜盘的力矩,控制柱塞缸通过球铰传递到斜盘上的力矩,以及轴承、球铰等位置上的摩擦力矩和柱塞与滑靴的惯性力矩、斜盘的惯性力矩.为简化分析,本文只考虑柱塞滑靴组件作用于斜盘上的力矩(包括惯性力矩)、偏置弹簧对斜盘的推力矩、控制柱塞缸作用在斜盘上的力矩和斜盘的惯性力矩以及摩擦力矩等，并将摩擦力矩折算到斜盘摆动阻尼系数里.

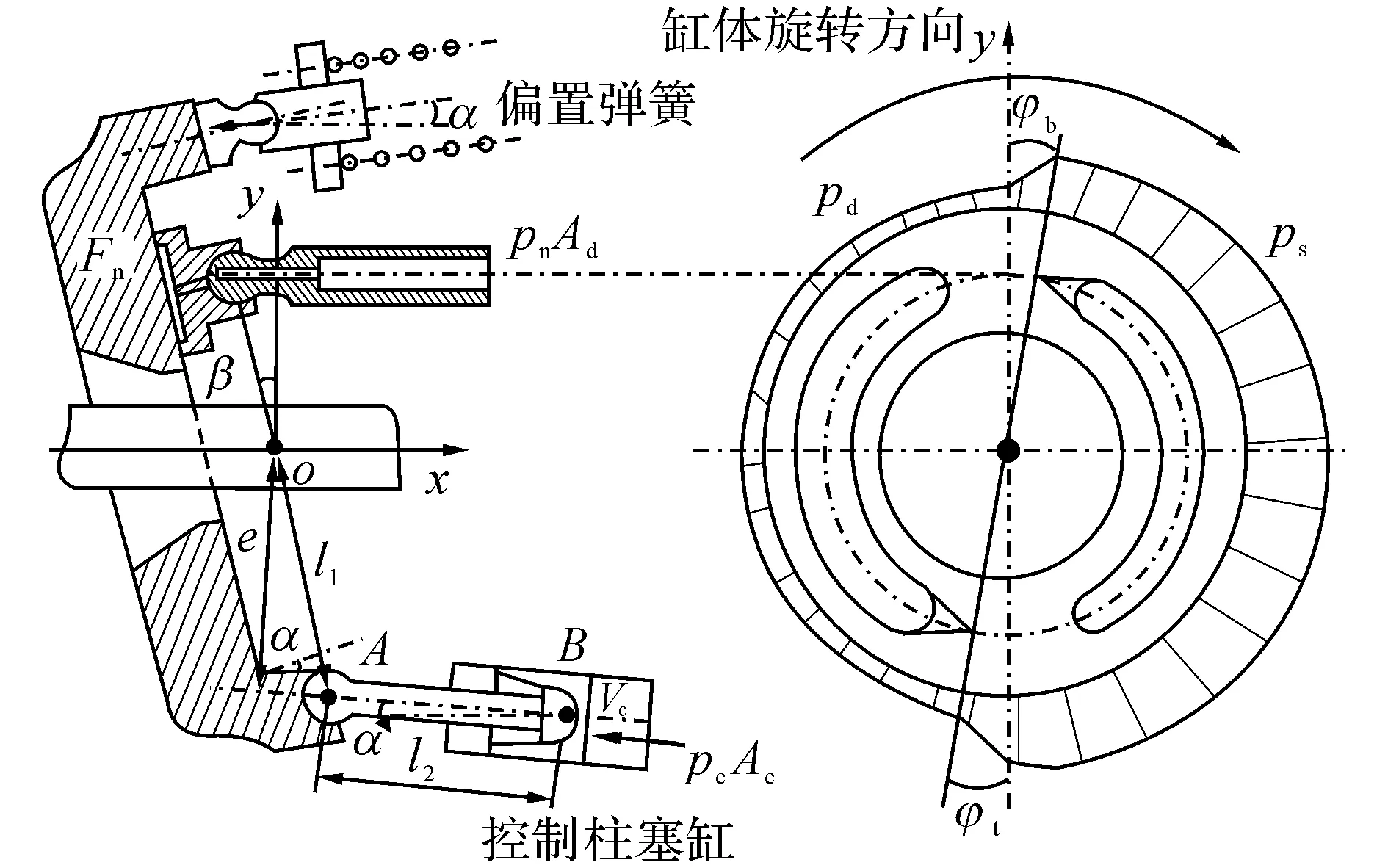
图4　斜盘受力示意图Fig.4　Force applied to swash plate

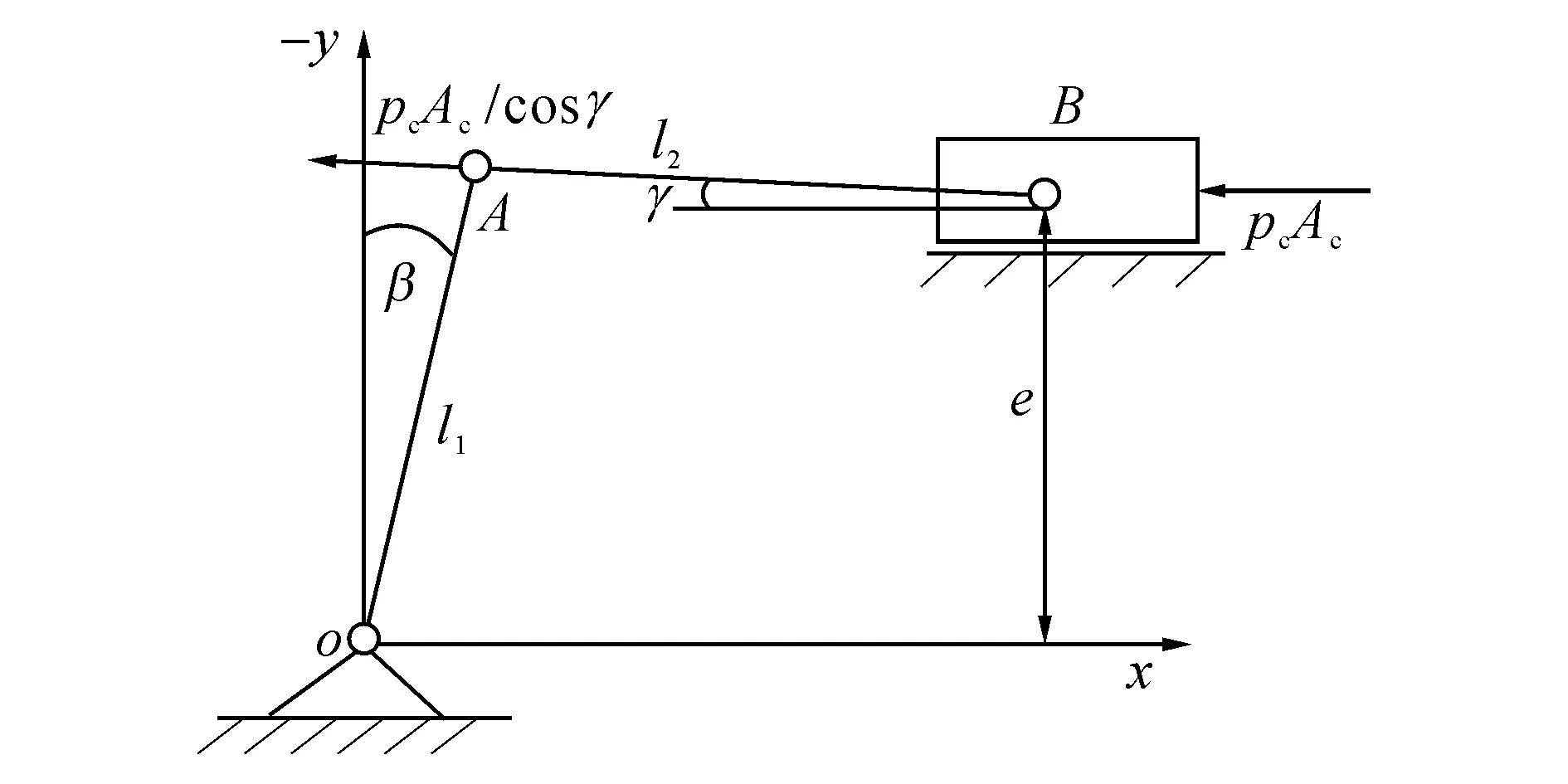
图5　斜盘-控制柱塞运动示意图Fig.5　Kinetic diagram of swash plate to its control actuator

根据受力分析,得斜盘运动方程[19]如下：

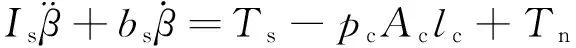
(3)

式中：Is为斜盘组件绕转动中心o的转动惯量,包括控制柱塞、偏置弹簧以及滑靴压盘组件随斜盘摆动的转动惯量；bs为斜盘组件摆动的黏性系数,包括斜盘支承轴承、控制柱塞及相关球铰的摩察力矩；Ts和Tn分别为偏置弹簧力矩和柱塞滑靴对斜盘的力矩.Ac和lc分别为柱塞面积和等效控制力臂.如图4所示,弹簧对斜盘的力方向和斜盘的法向夹角较小,故可以考虑为斜盘和弹簧力相互垂直,并且由于斜盘倾角改变较小,可认为偏置弹簧力矩为

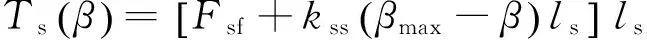
(4)

式中：Fsf为偏置弹簧在最大摆角时的预紧力,kss为偏置弹簧刚度,ls为偏置弹簧力矩.从图4中可以看出,由控制柱塞到斜盘摆角运动实质上是一个摇杆滑块机构,运动示意图如图5所示,在坐标系x-y定义其运动,由几何关系可得

(5)

式中：(xA,yA)和(xB,yB)分别为控制柱塞杆两端球头A、B的坐标.由于l1在y上的分量和e较为接近,γ较小,在实际计算中可以忽略不计,可得等效力臂为

lc=l1cos(β-γ)cosγ≈l1cosβ.

(6)

为改善压力调节机构动态特性,通常在柱塞缸容腔前设置阻尼孔或节流短管.考虑设置阻尼孔和节流短管的情况,控制腔压力pc即柱塞缸容腔(如图6所示)压力根据容腔公式为

图6　斜盘摆角控制柱塞缸示意图Fig.6　Schematic diagram of swash angle control actuator

(7)

Vc=Vco+Acl1(sinβmax-sinβ).

(8)

式中：Vc和Vco分别为控制柱塞容腔体积和初始容积,βe为油液等效弹性模量，qc为通过阻尼孔进出控制柱塞缸容腔的流量,pt为柱塞泵壳体压力,clc为腔体泄漏系数.

根据主阀阀芯位移xmv,qcm可由下式给出

(9)

式中：w为阀口面积梯度,ρ为油液密度,pcm为主阀出口小容腔Vcm内压力.对于由小容腔、节流短管及阻尼孔组成的结构来说,根据容腔公式以及流量-压降公式有

(10)

(11)

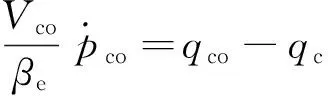
(12)

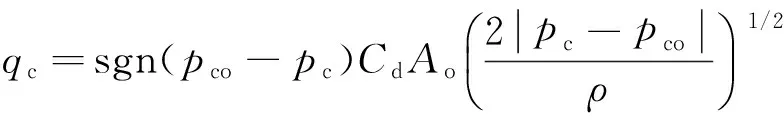
(13)

当泵在高转速时,考虑柱塞在缸体孔中往复运动产生的惯性力且认为柱塞在缸体孔中形成良好动压润滑并忽略摩擦力,对于单个柱塞来说,x轴力平衡方程式有

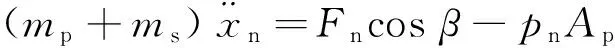
(14)

(15)

(16)

式中：mp和Ap分别为单个柱塞质量及底端面积,t为时间，xn和pn分别为第n个柱塞位移及柱塞腔压力,θ0及θn分别被第一个柱塞初始转角及第n个柱塞转角,R为柱塞分布圆半径,ω为泵的转速,Fn为第n个柱塞滑靴组件对斜盘的反作用力.根据图4,Fn的力臂ln可由下式表达

ln=Rcosθn/cosβ.

(17)

分析认为柱塞腔压力在等效压力过渡角范围内呈线性变化[19-21],如图4所示,当第n个柱塞腔在不同位置时,对应的压力为

(18)

其中,

式中：pd为泵吸油口压力,φb和φt分别为柱塞腔在上死点及下死点的等效压力过渡角.值得注意的是,φb和φt可为正或为负,图4给出的是压力过渡角为正的情况,实际中该值取决于配流盘的具体参数(如:减震槽/孔的尺寸、错配角等)以及泵的排量、工作压力等[21].

由于各个柱塞等间距分布,满足以下关系[20]：

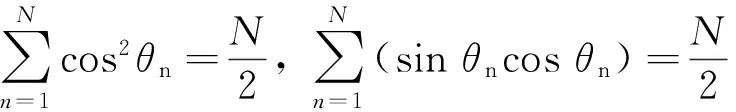
(19)

由式(14)～(19)可得

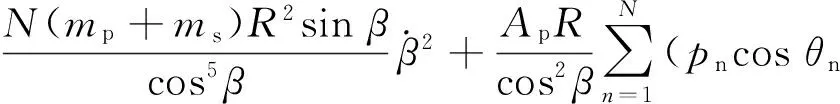
(20)

从式(20)中可以看出,对于变量泵来说,柱塞滑靴组件的惯性力实际上增大了斜盘组件摆动的转动惯量和阻尼.式(3)可改写为

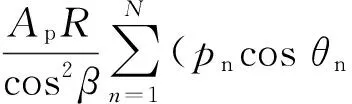
(21)

2.3出口压力流量转换模块

泵源流量经出口等效容腔作用,转化成压力[22],这一过程可表示为

(22)

qs=NApRωtanβ;

(23)

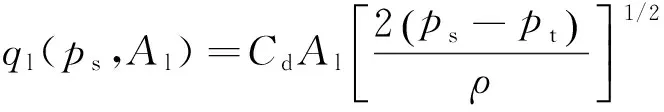
(24)

式中:ct为泵源总泄露系数,Al为负载节流阀开口面积.

根据以上建模过程,将各个模块连接起来,得到双压力柱塞泵压力调节机构动态特性框图如图7所示.式(10)～(13)表示的动态过程在图中简化处理为动态特性调节模块.压力调节机构由于阀口流量函数以及力臂随摆角实时变化,本质上是一个非线性系统.为尽可能准确地了解压力调节机构的动态特性以及相关状态变量在压力切换过程中变化情况,下文将依据图7对压力切换动态特性进行数值仿真.

图7　双压力泵压力调节机构动态特性框图Fig.7　Block diagram of pressure-controlled mechanism dynamic characteristics for DPP

3特性分析

利用Matlab/Simulink对双压力泵压力调节机构动态特性进行数值仿真.其中泵额定转速为3 600 r/min,节流阀开口面积为5 mm2,所用到的压力调节机构主要参数如表1所示.

表1　压力调节机构主要参数

3.1压力超调原因

分析过程中设定压力切换电磁阀1在10 ms内完成切换,在此过程中压力信号pp线性增加,直至等于ps,将表1中的参数代入图7,可得压力切换过程中阀芯位移、斜盘摆角及泵出口压力变化情况如图8所示.图中标出了压力切换过程中阀芯位移,斜盘摆角以及泵出口压力变化过程中前3个峰值的坐标.从图8(a)可以看出,在0.500 s泵由高压向低压切换时,压力信号pp加载到阀端面积As上,主阀阀芯右移(图3),高压油液进入控制腔,导致斜盘摆角迅速减小,在0.506 s斜盘摆角第一次达到调定值,如图8(b)所示.此时由于出口容腔的作用,压力并未达到21.0 MPa,阀芯继续保持在右位,导致斜盘摆角继续减小,直到0.518 s泵出口压力第一次达到调定压力,如图8(c)所示.此时阀芯处于中位,斜盘摆角最小,由于斜盘转动惯量相对较大,斜盘需要一段时间回到设定位置,使得泵出口压力继续下降,阀芯向左移动,斜盘在偏置弹簧力的作用下开始向设定值回复,直至0.530 s达到设定值,压力达到最小值,超调峰值达到-3.5 MPa,阀芯停留在最左位.此后压力开始回升,在0.543 s达到设定压力,阀芯右移开始新一轮循环.由于阻尼的存在,阀芯位移、斜盘摆角及压力振动幅值逐渐减小,使得压力最终稳定在21.0 MPa.类似地,泵由低压向高压切换时,作用在阀端面积As的压力pp撤掉,使得阀迅速向左移动,斜盘摆角增大,泵出口压力第一次达到调定压力后,压力继续上升,直到超调峰值达到4.9 MPa.斜盘仍需一段调节过程,最终稳定在设定值.值得注意的是,压力切换过程中出口节流阀开度不变,但由于泵的泄漏量随压力增加而变大,使得斜盘摆角最终稳定在不同的值上,两者之间差值为Δβ,如图8(b)所示.

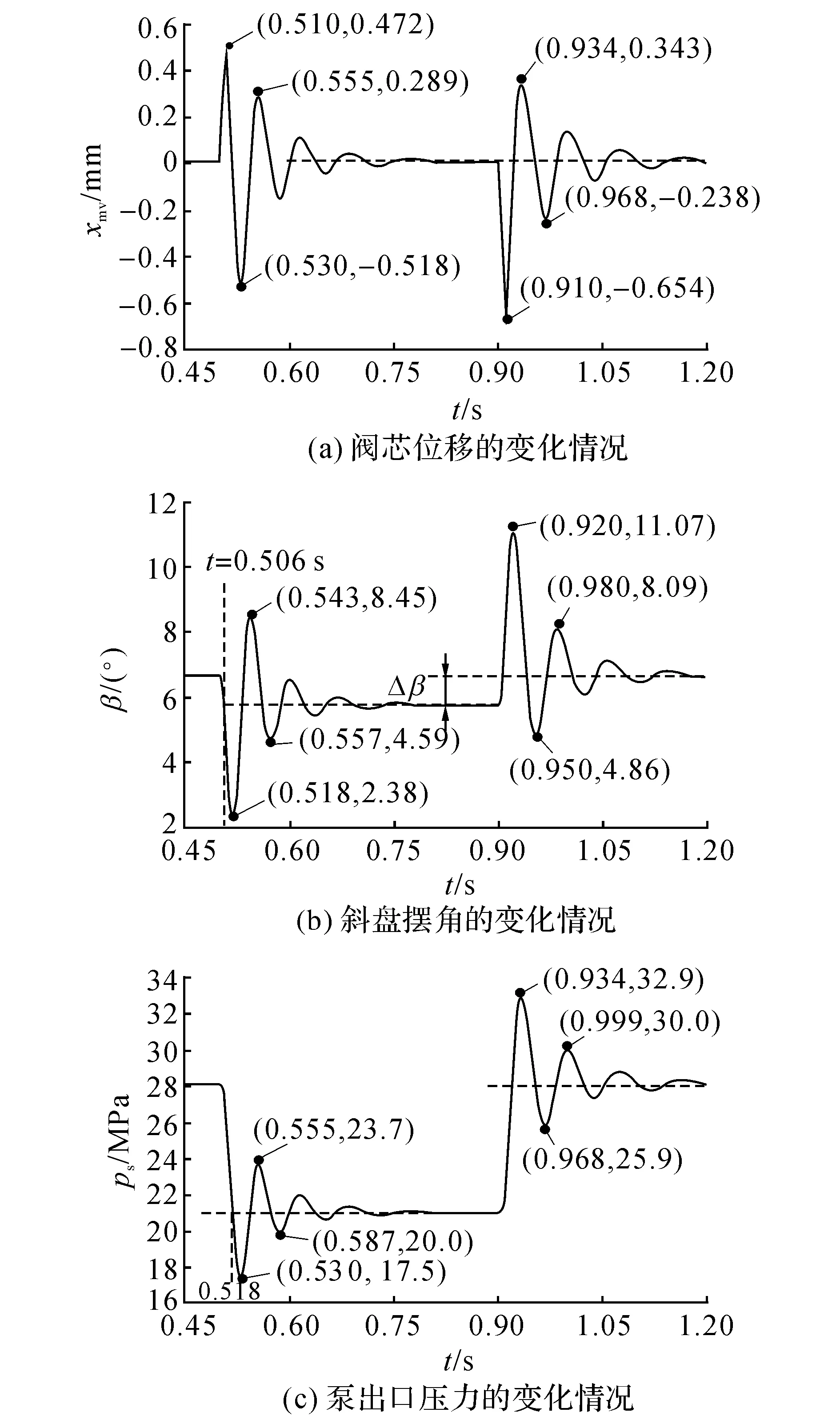
图8　压力切换时阀芯位移、斜盘摆角以及泵出口压力的变化情况Fig.8　Change of spool traverse,swash plate angle and pump discharge pressure during dual-pressure switch process

3.2改进措施

从以上分析过程中可以看出,双压力泵在压力切换过程中出现压力超调的原因主要是斜盘摆角初次达到设置值时,在出口容腔的滞后作用下,压力并未随之上升或下降,致使斜盘摆角继续增加或减少；泵初次达到调定压力后,由于斜盘转动惯量较大(滞后环节),斜盘需经历加减速的振荡过程后才能回复到设置值,在这个过程中出现压力超调和振荡现象.其实质是一个滞后系统,因此降低压力超调幅值最有效的方法是降低斜盘以及泵出口等效容腔这两个滞后环节(图7中用虚线框标出)带来的影响.后者可以通过减小等效容腔体积,使得积分系数βe/Vd增大实现.

斜盘组件等效转动惯量随着泵的结构尺寸已经基本确定,因此更多地可以从增益以及阻尼调节的角度来改善泵在压力切换时的动态特性.对于双压力泵来说,在控制柱塞腔前设置阻尼孔或节流短孔是一种可行的调节动态特性的方法(见图7).节流短孔起着连接主阀和柱塞控制腔的作用,尺寸已经基本限定,因此着重考虑阻尼孔直径变化对压力调节机构动态特性的影响.从式(3)、(7)及(10)～(13)可以看出,阻尼孔直径的调节实质上改变了进入控制腔的流量,影响控制腔压力建立过程,从而使斜盘摆动加快或减慢.图9给出了减小泵出口等效容腔体积以及在控制柱塞腔前设置阻尼孔对泵压力切换动态特性的影响.

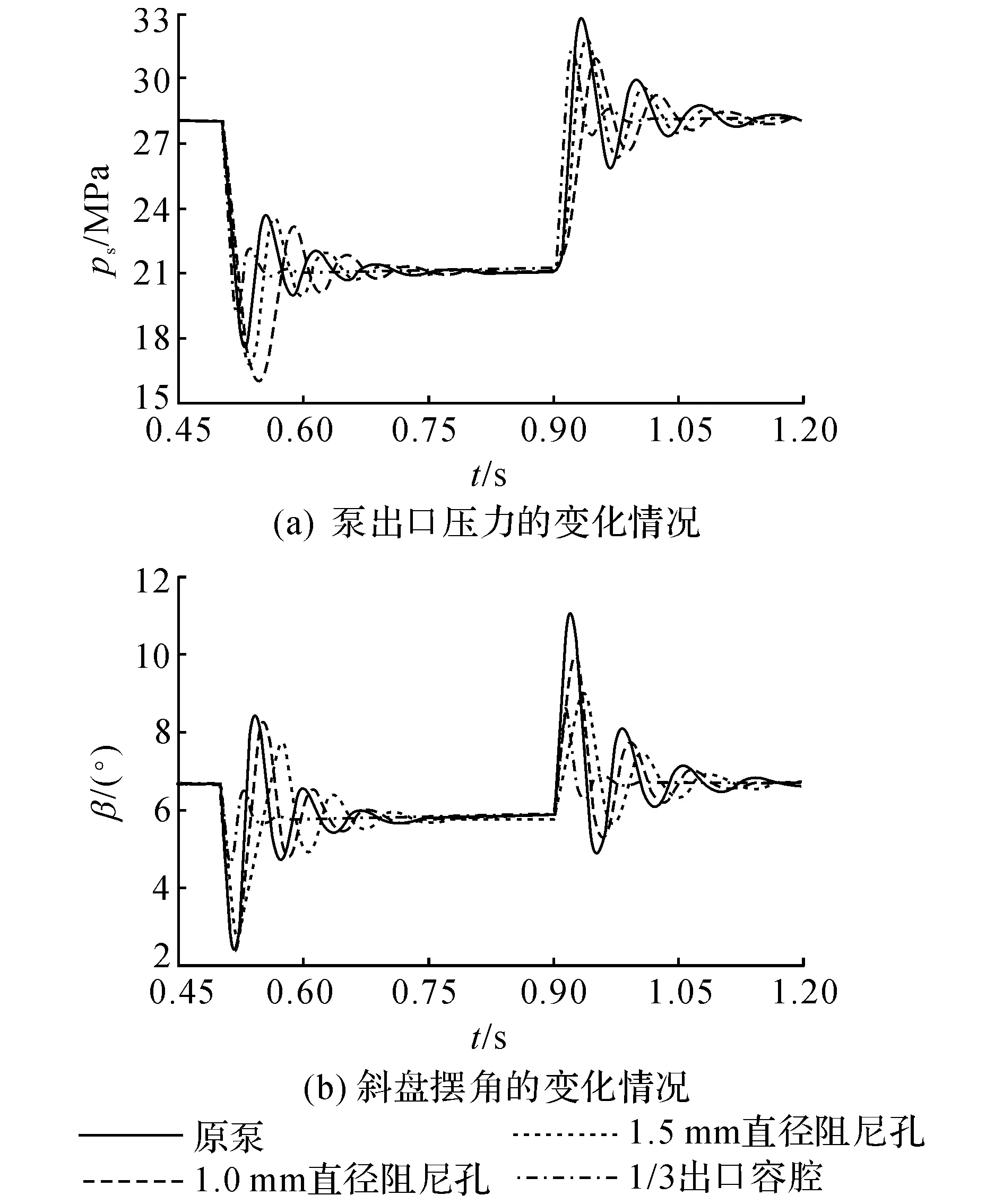
图9　压力切换时斜盘摆角及泵出口压力变化情况Fig.9　Change of swash plate angle and pump discharge pressure during dual-pressure switch process

从图9中可以看出，将泵出口等效容腔体积缩小为原来的1/3,能够有效地减轻容腔滞后环节带来的影响,泵在由高压向低压切换时,斜盘摆角最小值仅为4.63°,泵压力超调值仅为-1.8 MPa.泵由低压向高压切换时,斜盘摆角最大值达到8.60°,压力超调值仅为3.3 MPa,相比原泵降低了1.6 MPa；同时泵出口压力响应时间以及稳定时间有所降低.可以预见,泵出口等效容腔越小,压力超调峰值越小,然而实际中出口等效容腔体积降低到一定程度时(200 mL左右)将显著增大泵出口压力脉动,而当容腔体积大于200 mL时继续增大出口等效容腔对压力脉动影响不大[23],因此在满足泵压力脉动幅值条件下尽可能降低泵出口等效容腔,将有效地降低双压力泵压力调节过程中的压力超调幅值.

在控制柱塞腔前设置阻尼孔降低了泵压力切换时的斜盘摆角超调峰值,但同时也使得斜盘运动速度变慢,使得斜盘向设定值回复的时间变长,可能会增大压力超调峰值.图9(b)中,泵由高压向低压切换时,随着阻尼孔直径的减小,斜盘摆角超调峰值和斜盘运动速度均缓慢下降,加大了超调峰值,在阻尼孔直径为1.0 mm时压力超调峰值达到了-5.0 MPa；而当泵由低压向高压切换时,斜盘摆角超调峰值在阻尼孔直径为1.5 mm和1.0 mm时,分别下降了1.00°和2.00°,角度减小对压力的影响超过斜盘运动速度减慢带来的影响,压力超调峰值有不同的程度地降低.阻尼孔使泵出口压力响应速度变慢,选用时需兼顾泵的动态响应要求.

从式(22)可以看出,当阀芯处于右位(qcm>0)时,斜盘摆角减小,用于控制斜盘摆角的一部分流量取自泵出口容腔,使得泵出口压力下降较快；反之斜盘摆角增大时控制柱塞腔排出的流量回到泵壳体内，在一定程度上增大了高压向低压切换时的压力超调幅值.因此在阀芯处于右位时,当阀口开度一定时,应适当降低面积梯度或者减小阀口前后压差：阀口面积梯度降低可以通过改变阀口窗口参数及形状实现；通过合理设计配流盘以减小等效压力过渡角φb或φt,调节柱塞滑靴组件对斜盘的平均合力矩[21,24-25],从而增大控制柱塞腔体内平均压力来降低主阀阀口前后压差.对于滞后系统来说,增大增益可能会造成斜盘摆角峰值加大,造成系统失稳；降低增益使系统响应变慢,斜盘向设定值运动时间加长,加剧压力超调现象,增益的确定是一个优化问题.因此只给出了增大柱塞滑靴组件对斜盘平均力矩(调节配流盘,使平均力矩增大100 Nm)及配合使用阻尼孔,降低出口等效容腔等方法压力切换时的泵出口压力情况,如图10所示.

图10　压力切换时泵出口压力ps变化情况Fig.10　Discharge pressure ps during dual-pressure switch process

从图10中可以看出,增大柱塞滑靴组件对斜盘平均力矩,会轻微降低泵由高压向低压切换时的压力超调峰值,增大低压向高压切换时的压力超调峰值.从式(3)可以看出,平均力矩的增加会增大控制柱塞腔体内平均压力,导致阀芯处于左位时压差增大,相当于等效增大了流量增益；合理设计配流盘以增大柱塞滑靴组件对斜盘平均力矩和阻尼孔配合使用,避免了单独使用阻尼孔时,泵由高压向低压切换时压力超调峰值增大的现象；将上述方法综合起来,泵压力切换时压力切换峰值分别为-1.8和2.8 MPa,相比原泵分别下降了48.6%和42.9%.在实际中配流盘的设计往往集中在降低流量脉动,提高容积效率等方面.从以上分析可以看出,进行配流盘的优化时还应兼顾到其对泵动态特性的影响,从而使泵性能达到最优.

4结论

(1) 双压力泵在压力切换过程中出现的压力超调现象,主要是由泵出口容腔及斜盘这2个滞后环节引起的.

(2) 合理设计配流盘、设置阻尼孔及降低泵出口等效容腔体积等方法能够降低压力超调峰值,但不可避免地会对泵的压力脉动和响应时间造成影响.在实际使用中,应避免过小的泵出口等效容腔体积(小于200 mL)及阻尼孔直径,配合使用以上方法,从而使泵的性能达到最优.

参考文献(References)：

[1] 王占林. 飞机高压液压能源系统[M]. 北京：北京航空航天大学出版社, 2004.

[2] 卢宁,付永领,孙新学. 基于AMEsim的双压力柱塞泵的数学建模与热分析[J]. 北京航空航天大学学报,2006, 32(9):1055-1059．

LU Ning, FU Yong-ling, SUN Xin-xue. Digital modeling of double press axial piston pump and its thermal analysis basing on AMEsim [J]. Journal of Beijing university of Aeronautics and Astronautics, 2006, 32(9):1055-1059．

[3] 陈焕明,刘卫国,习仁国, 等. 双压力柱塞泵建模与仿真研究[J]. 机床与液压,2012,40(8):71-74．

CHEN Huan-ming, LIU Wei-guo, XI Ren-guo, et al. Research on the modeling and simulation of the double-pressure axial piston pump [J]. Machine Tool and Hydraulics, 2012,40(8):71-74．

[4] FIEBING C, LU X J, SMOLKA S. Pressure compensator (PC) pressure overshoot analysis and experimental research of an open circuit pump [C] ∥Fluid Power and Mechatronics (FPM), Harbin:IEEE, 2015: 910-913．

[5] MANDAL N P, SAHA R, MOOKHERJEE S, et al. Pressure compensator design for a swash plate axial piston pump [J]. Journal of Dynamic Systems, Measurement, and Control, 2014, 136(2): 021001．

[6] SCHOENAU G J, BURTON R T, KAVANAGH G P. Dynamic analysis of a variable displacement pump [J]. Journal of Dynamic Systems, Measurement, and Control, 1990, 112(1): 122-132.

[7] ALY A A. Flow rate control of variable displacement piston pump with pressure compensation using neural network [J]. Journal of Engineering Science, 2007, 33(1): 199-209．[8] MANRING N D. Designing a control and containment device for cradle-mounted, axial-actuated swash plates [J]. Journal of Mechanical Design, 2002, 124(3): 456-464．

[9] MANRING N D. Designing a control and containment device for cradle-mounted, transverse-actuated swash plates [J]. Journal of Mechanical Design, 2001, 123(3): 447-455．

[10] BAHR M K, SVOBODA J, BHAT R B. Vibration analysis of constant power regulated swash plate axial piston pumps[J]. Journal of Sound and Vibration, 2003, 259(5): 1225-1236．

[11] ACHTEN P. Dynamic high-frequency behavior of the swash plate in a variable displacement axial piston pump [J]. Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, 2013, 227(6): 529-540.

[12] KIM J H, JEON C S, HONG Y S. Constant pressure control of a swash plate type axial piston pump by varying both volumetric displacement and shaft speed [J]. International Journal of Precision Engineering and Manufacturing, 2015, 16(11): 2395-2401．

[13] MANDAL N P, SAHA R, SANYAL D. Effects of flow inertia modelling and valve-plate geometry on swash-plate axial-piston pump performance [J]. Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, 2011: 0959651811426508．

[14] 陈龙, 常真卫, 翟江, 等. 航空柱塞泵系统建模与仿真研究[J]. 液压气动与密封, 2015 (7): 69-72．CHEN Long, CHANG Zhen-wei, ZHAI Jiang, et al. Research on system modeling and simulation of aircraft piston pump [J]. Hydraulic Pneumatics and Seals, 2015 (7): 69-72．

[15] 童水光, 王相兵, 钟崴, 等. 基于虚拟样机技术的轴向柱塞泵动态特性分析[J]. 机械工程学报, 2013, 49(2): 174-182．

TONG S G, WANG X B, ZHONG W, et al. Dynamic characteristics analysis on axial piston pump based on virtual prototype technology [J]. Journal of Mechanical Engineering, 2013, 49(2): 174-182．

[16] ROCCATELLO A, MANCS, NERVEGNA N. Modelling a variable displacement axial piston pump in a multibody simulation environment [J]. Journal of Dynamic Systems, Measurement, and Control, 2007, 129(4): 456-468．

[17] KALIAFETIS P, COSTOPOULOS T. Modelling and simulation of an axial piston variable displacement pump with pressure control [J]. Mechanism and Machine Theory, 1995, 30(4): 599-612．

[18] 魏湉. 航空柱塞泵压力脉动特性研究[D]. 杭州：浙江大学, 2013.

WEI Tian. Research on the pressure pulsation of the aviation piston pump [D]. Hangzhou:Zhejiang University,2013．

[19] MANRING N D, JOHNSON R E. Modeling and designing a variable-displacement open-loop pump [J]. Journal of Dynamic Systems, Measurement, and Control, 1996, 118(2): 267-271．

[20] MANRING N D, MEHTA V S. Physical limitations for the bandwidth frequency of a pressure controlled, axial-piston pump [J]. Journal of Dynamic Systems, Measurement, and Control, 2011, 133(6): 061005．

[21] WANG S. Novel piston pressure carryover for dynamic analysis and designs of the axial piston pump [J]. Journal of Dynamic Systems, Measurement, and Control, 2013, 135(2): 024504．

[22]KEMMETMÜLLER W, FUCHSHUMER F, KUGI A. Nonlinear pressure control of self-supplied variable displacement axial piston pumps [J]. Control Engineering Practice, 2010, 18(1): 84-93．

[23] 高锋. 飞机液压系统泵-管路振动特性研究[D]. 杭州：浙江大学, 2013. GAO Feng. Investigation into the vibration characteristic of the pump and connected pipeline in the aircraft hydraulic system [D]. Hangzhou:Zhejiang University, 2013．[24] SEENIRAJ G K, IVANTYSYNOVA M. Impact of valve plate design on noise, volumetric efficiency and control effort in an axial piston pump [C] ∥ASME 2006 International Mechanical Engineering Congress and Exposition. Chicago:ASME, 2006: 77-84．

[25] KUMAR S G, IVANTYSYNOVA M. A multi-parameter multi-objective approach to reduce pump noise generation [J]. International Journal of Fluid Power, 2011, 12(1): 7．

DOI:10.3785/j.issn.1008-973X.2016.03.001

收稿日期：2015-06-15.

基金项目：国家自然科学基金资助项目(51275450);国家“973”重点基础研究发展规划资助项目(2014CB046403)；浙江大学基本科研业务费专项资金资助项目(科研发展专项)(2013FZA4004).

作者简介：欧阳小平(1974-)，男，副教授，博士，从事航空液压、电液控制及外骨骼机器人研究. ORCID: 0000-0002-2090-7123. E-mail: ouyangxp@zju.edu.cn

中图分类号：TH 137.7

文献标志码：A

文章编号：1008-973X(2016)03-08-0397

Dynamic characteristics of dual-pressure switch for aircraft piston pump

OUYANG Xiao-ping, LI Lei, FANG Xu, YANG Hua-yong

(StateKeyLaboratoryofFluidPowerandMechatronicSystem,ZhejiangUniversity,Hangzhou310027,China)

Abstract:The dynamic mathematic model of the pressure-controlled mechanism was established and the numerical simulation investigation was conducted to analyze the causes of pressure overshoot in order to reduce the pressure overshoot amplitude. Analysis show that the pump discharge equivalent chamber and the swash plate are the main causes of the pressure overshoot during the dual pressure switch process. Methods for minimizing the pressure overshoot amplitude were proposed, such as lowering the discharge equivalent chamber volume of the pump and configuring an adjustable damp hole. The simulation results indicate that the pressure overshoot amplitudes decrease by 48.6% with dual-pressure piston pump (DPP) switching from high operating pressure to low operating pressure and decrease by 20.4% vice versa at one third of the DPP discharge equivalent chamber volume. While the damp hole can effectively suppress the pressure overshoot amplitude with DPP switching from high operating pressure to low operating pressure, and can increase the pressure overshoot amplitude vice versa. Therefore, these methods should be applied in a comprehensive way.

Key words:dual-pressure piston pump (DPP); pressure switch; pressure overshoot