球对称玻色-爱因斯坦凝聚中低能呼吸模的朗道阻尼和频移
2016-07-31符豫东马晓栋
马 瑞, 符豫东, 马晓栋
(新疆师范大学 物理与电子工程学院,新疆 乌鲁木齐 830054)
球对称玻色-爱因斯坦凝聚中低能呼吸模的朗道阻尼和频移
马 瑞, 符豫东, 马晓栋*
(新疆师范大学 物理与电子工程学院,新疆 乌鲁木齐 830054)
文章采用平均场理论近似研究球对称玻色-爱因斯坦凝聚中三个低能呼吸模的朗道阻尼和频移,解析计算阻尼系数和频移大小及它们的温度依赖,以期对理论和实验研究提供一定的参考价值。
玻色-爱因斯坦凝聚;朗道阻尼和频移;哈特里-福克-博戈留波夫近似;托马斯-费米近似
玻色-爱因斯坦凝聚(Bose-Einstein condensate,简称BEC)是大量微观粒子宏观占据一个量子态的现象。集体激发是BEC研究中最基本的问题之一。阻尼和频移是集体激发的主要特征(集体激发频移的衰减和改变),是两个相伴存在的物理现象。
文章计算球对称BEC中三个低能呼吸模的朗道阻尼和频移。其中一个准粒子吸收一个集体模的能量变成另一个准粒子是阻尼和频移的朗道机制。
采用哈特里-福克-博戈留波夫(Hartree-Fock-Bogoliubov,简称HFB)平均场近似的频移改变微扰理论公式[1],并在应用频移改变的微扰理论公式中考虑元激发的弛豫及弛豫之间的正交关系[2-4]。采用解析方法计算,由于托马斯-费米近似(Thomas-Fermi-Approximation,简称TFA)是目前唯一的解析方案,而它存在不可控制的发散[5],因此采用在基态波函数中引入消除发散参量q的改进的TFA(beyond TFA,简称bTFA)[6-9],其中q取1,即基态波函数取高斯分布函数的一级近似[2-4]。
1 朗道阻尼和频移计算中有关理论公式
囚禁在谐振频率为ωho球对称势阱(m是原子质量,Wh0是谐振频率)的稀薄BEC原子气体基态

元激发本征函数bTFA解为
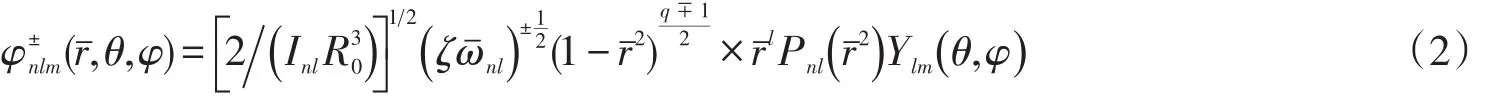
其中ζ=ℏωho/2μ,Ylm(θ,φ)是球谐函数是归一化积分而函数P(x)满足超几何方程,相应的本征值而是TFA的本征值,元激发频率通过引入=ω/ωho进行了无量纲化。本征函数及相应的本征值用 j=(n,l,m)来标记,主量子数 n=0,1,…,轨道角动量量子数 l=0,1,…,投影量子数m=0,±1,±2…±l。其本征值是 2l+1重简并的。
频率为ωˉi的准粒子通过吸收一个频率为ωˉ0激发模变成了频率为ωˉj的准粒子,集体模的频率修正为是以为标度的无量纲的阻尼强度,而是无量纲温度,是以为标度的无量纲三模耦合矩阵元且

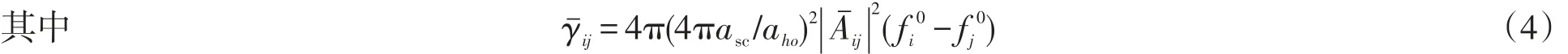
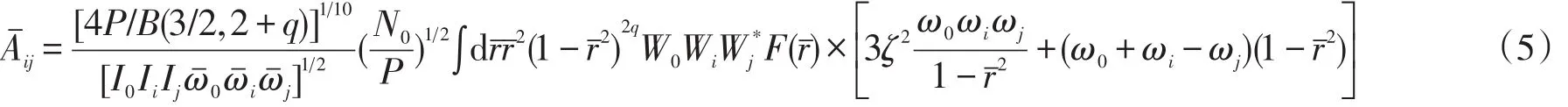
如前文所述,以上各式中参量q=1是为了消除在TFA下发散而引入的。
在频移改变微扰理论公式中考虑元激发的弛豫及其弛豫之间的正交关系得到朗道阻尼和频移的计算公式,分别为

其中近似地认为阻尼系数正比于频率。
2.计算及结果
考虑球对称势阱中87Rb原子(asc=5.82×10-9),研究的集体模是单极子呼吸模(n,l,m)=(1,0,0),偶极子呼吸模(n,l,m)=(2,0,0)和四极子呼吸模 (n,l,m)=(3,0,0)。三个集体模的频率分别为 ω0=2.23607,ω0=3.74166和 ω0=5.19615(以ωho为单位),三个集体模的波戈留波夫振幅分别为
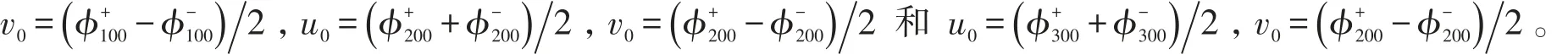
阻尼强度用(4)及(5)式来计算。在图1和图2及其插图中,分别给出了偶极子模和四极子模阻尼和频移有贡献的各个跃迁频率 ωij(ωij=ωj-ωi,以ωho为单位)的阻尼强度 γij(以为单位)。准粒子跃迁(ni,li,mi)→(nj,lj,mj)满足选择条件 li=lj和 mi=mj。取文献[10]中的参量 N0=200000和 ωho=1146Hz,取温度 KBT/μ=1(对应 T=238.7nK,其中μ=27.3ℏωho)。图1和图2及其插图中箭头指向偶极子模和四极子模的频率ω0,线的位置对应着允许的跃迁频率 ωij而其高度给出 γij的计算值。
能级量子数大的准粒子本征函数振荡很快且极大值远离凝聚中心,另外量子数大能级能量高,其玻色布居因子小,因此量子数大的能级之间的跃迁耦合矩阵元小。通过仔细地考虑,在计算中选取n=0,1,2,3,4,5,6而 l满足 l≤25的能级(n ,l,m )。
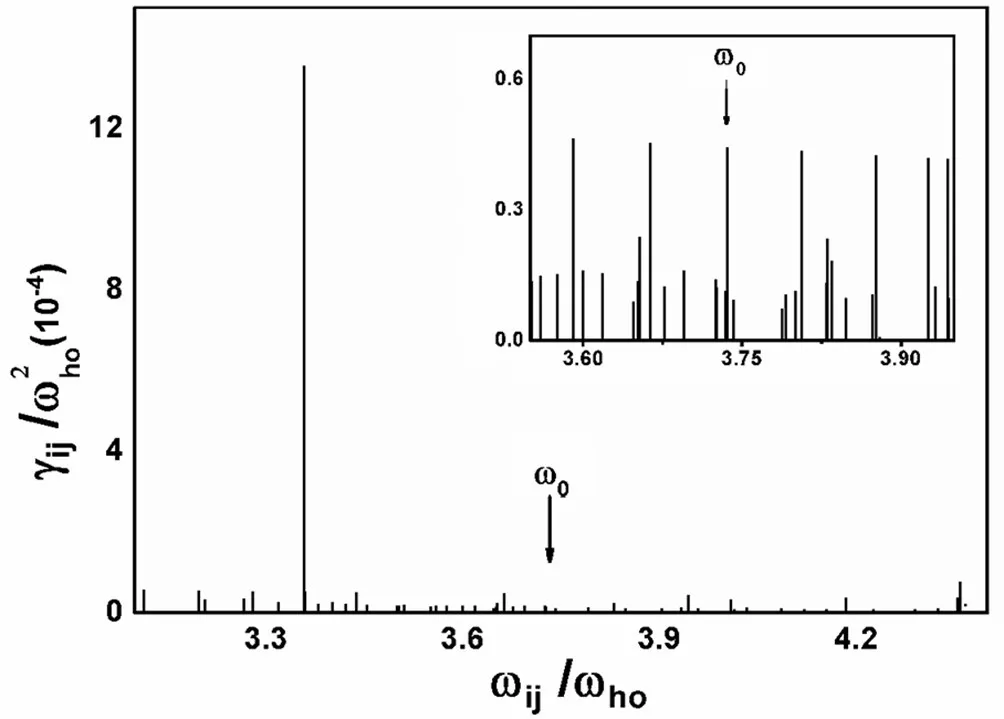
图1 以跃迁ωij为变量的偶极子模阻尼强度γij函数线状图
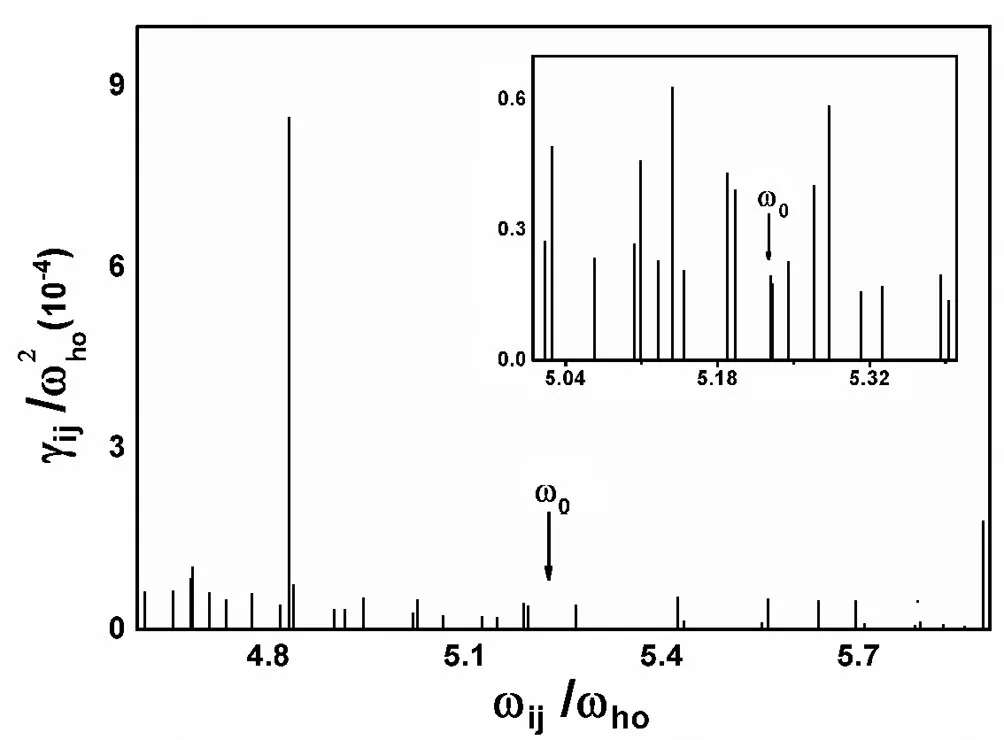
图2 以跃迁ωij为变量的四极子模阻尼强度γij函数线状图
阻尼系数用(6)式来计算,并采用迭代的方法。图3和图4分别给出了偶极子模和四极子模在温度KBT/μ=0.4,0.8,1.2(相当于T=15.5,31.0,46.5 nK,其中μ=6.3ℏωho)下 γ0(以ωho为单位)随 γ(以 ωho为单位)变化的关系。在图3和图4中,取文献[11]中的参量N0=6000和 ωho=810Hz,用星号表示的三点处γ0=γ。图3在KBT/μ=0.4,0.8,1.2下的偶极子模阻尼系数的数值在此三点给出,分别为0.01345,0.0280,0.0444,相当于10.9,22.7,36.0 s-1。图4在KBT/μ=0.4,0.8,1.2下的四极子模阻尼系数的数值在此三点给出,分别为0.00903,0.0225,0.0389,相当于7.3,18.2,31.5 s-1。
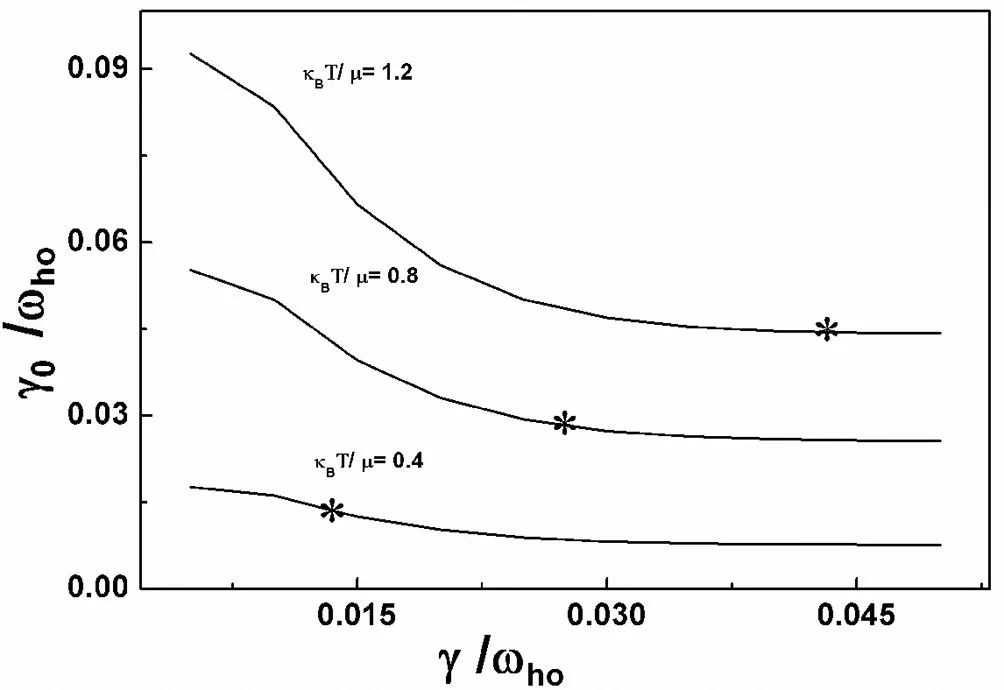
图3 偶极子模关于朗道阻尼的γ0随γ变化函数图
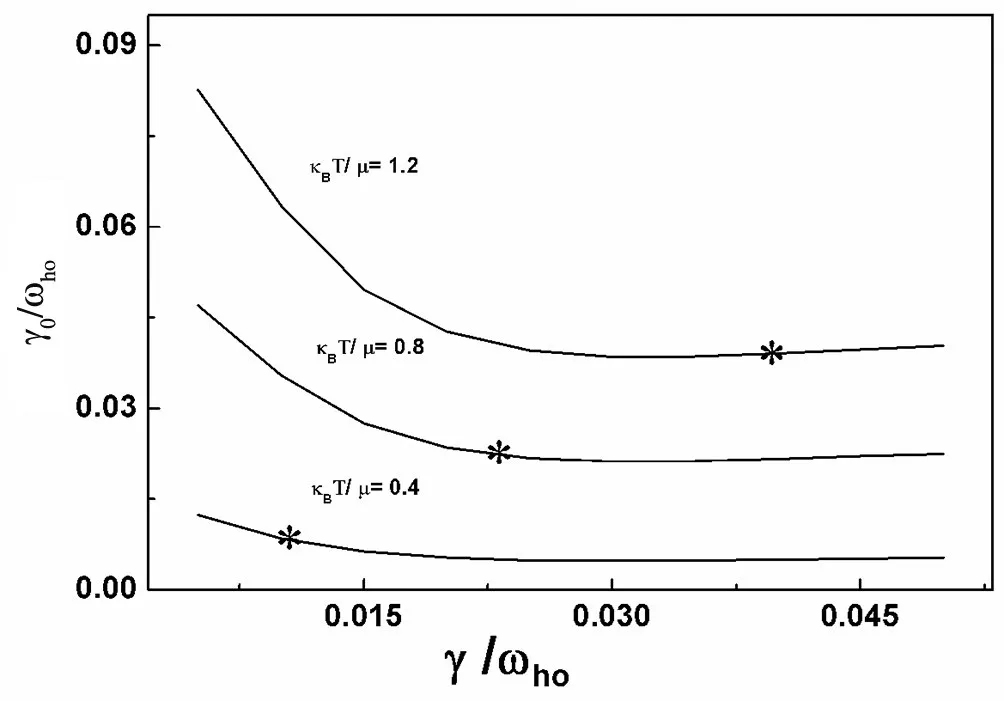
图4 四极子模关于朗道阻尼的γ0随γ变化函数图
频移用(7)式来计算,并采用阻尼系数 γˉ0的计算结果。图5和图6给出了单极子模,偶极子模和四极子模的阻尼 γ0(以s-1为单位)和频移(以 ω的变化来表示,以 ωho为单位)随温度 T(以nK为单位)变化的函数关系,取文献[11]中的参量 N0=6000和 ωho=810Hz。
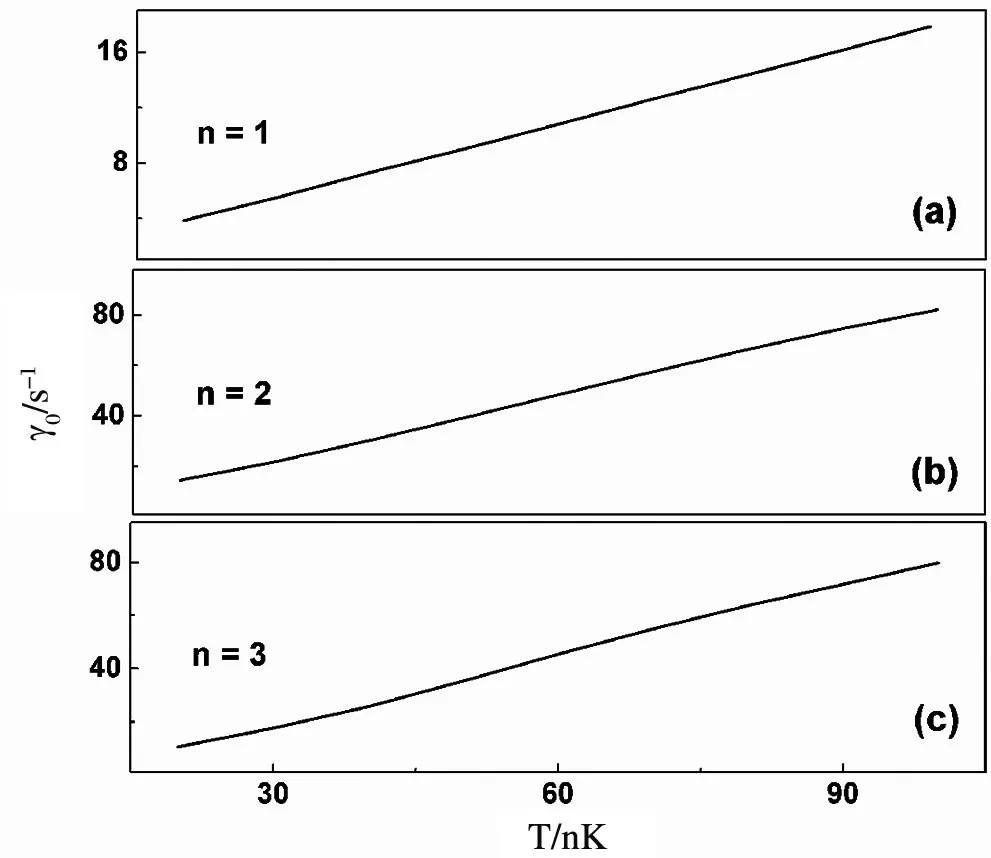
图5 凝聚体集体模的朗道阻尼系数γ0随温度T的变化图
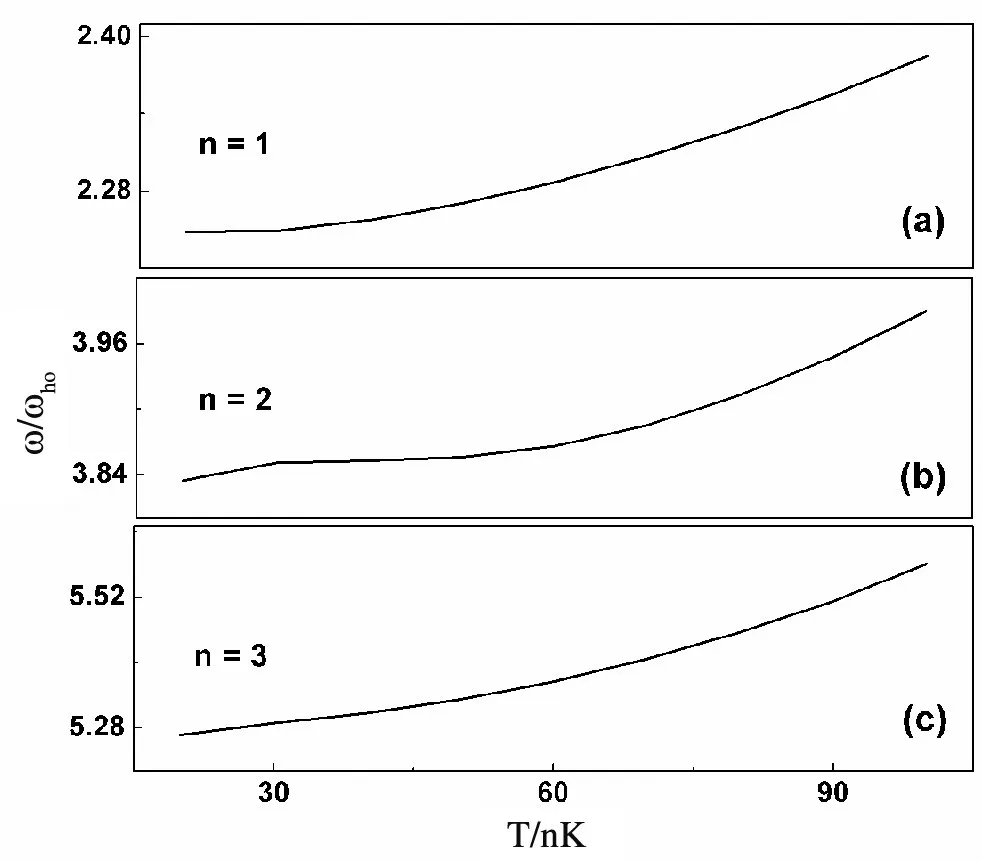
图6 凝聚体集体模的朗道频移ω随温度T的变化图
图7和图8给出了单极子模,偶极子模和四极子模的阻尼 γ0(以 s-1为单位)和频移(以 ω的变化表示,以ωho为单位)随温度 T(以nK为单位)的函数关系,取文献[10]中的参量 N0=200000和 ωho=1146Hz。
3 结论
文献[2]和文献[3]分别计算了雪茄形铷原子BEC凝聚体中单极子模和碟形铷原子BEC凝聚体中四极子模的朗道阻尼和频移。文献[2]和文献[3]的解析计算结果分别与文献[10]和文献[11]的实验结果符合。并且文献[2]和文献[3]在计算过程中分别采用了文献[10]和文献[11]完全相同的实验参量。这说明在频移改变微扰理论公式中考虑元激发的弛豫及弛豫之间的正交关系是合理的。文献[4]计算了球形铷原子BEC凝聚体中单极子低能模的朗道阻尼和频移。由于没有球对称系统的实验结果,文献[4]关于球形凝聚体的解析计算结果与文献[10、11]关于轴对称凝聚体的实验结果进行了间接对比,并讨论计算结果与实验结果不同的原因。文献[4]还用文献[12]在平均场理论的频移微扰公式中引入洛伦兹分布函数的方法并采用文献[12]完全相同的系统参量计算了阻尼,文献[4]的解析结果与文献[12]的数值模拟结果相符。从而对解析方案中基态波函数取高斯分布函数的一级近似进行了验证。采用文献[2-4]相同的方法,计算了球对称玻色-爱因斯坦凝聚中偶极子模和四极子模的朗道阻尼和频移。为了比较将文献[4]中的单极子呼吸模的计算结果也列入阻尼和频移的计算图中。文章对阻尼和频移的计算结果可以作为预言,可以为理论和实验提供一定的参考价值。值得一提的是,三个低能呼吸模阻尼和频移的计算结果基本符合我们在计算中采用的阻尼和频移成正比的近似。
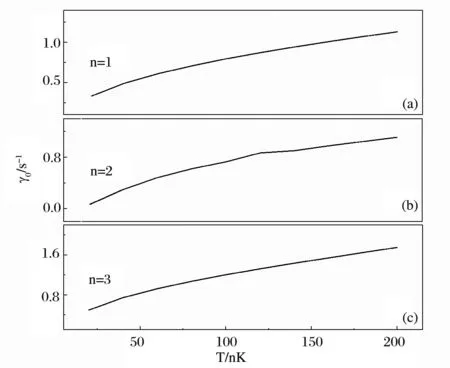
图7 同图5,但参量另取为N0=200000和ωho=1146Hz
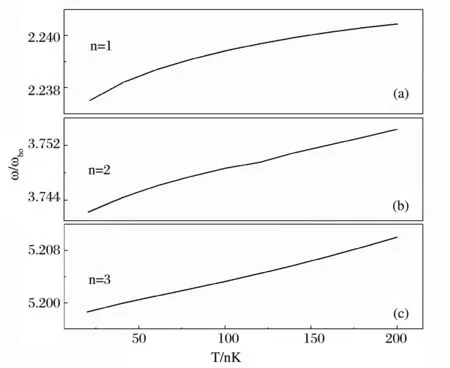
图8 同图6,但参量另取为N0=200000和ωho=1146Hz
[1]S.Giorgini,Damping in dilute Bosegases:amean-field approach[J].Phys.Rev.A,1998,57:2949-2957.
[2]Z.Chai,Y.Zhou,and X.Ma.Landau dampingand frequency-shiftofmonopolemode in an elongated rubidium Bose-Einstein Condensate[J].Ac-ta.Phys.Sin,2013,13:130307(1)-130307(8).
[3]R.Arzigul,S.Peng,and X.Ma.Landau damping and frequency-shift of quadrupolemode in a disc-shaped rubidium Bose-Einstein Condensate[J].Chin.Phys.B,2014,9:090311(1)-090311(7).
[4]S.Peng,R.Arzigul,and X.Ma.Landau damping and frequency-shiftofamonopolemode in a sperical rubidium Bose-Einstein condensate[J].J. At.Mol.Phys,2015,6:1018-1026.
[5]C.J.Pethick and H.Smith,Bose-Einstein Condensation in diluteGases(Cambridge Univer-sity Press,Cambridge[M].2002.
[6]Y.L.Ma and S.T.Chui.Analytical expressions for the hydrodynamic excitation spectrum of Bose-Einstein condensates in axially anisotropic traps[J].Phys.Rev.A,2002,65:053610(1)-053610(6).
[7]X.Ma,Y.Zhou,Y.L.Ma,and G.Huang,Landau damping of collectivemodes in aharmonically trapped Bose-Einstein condensate[J].Chin.Phys. 2006,15:1871-1878.
[8]X.Ma,Y.L.Ma,and G.Huang.Analytical calculationson Landau damping of collectivemodes in anisotropic Bose-Einstein condensates[J].Phys. Rev.A,2007,75:013628(1)-013628(8).
[9]X.Ma,Y.L.Ma,and G.Huang.Landau Damping of Collective Modes in a Disc-Shaped Bose-Einstein Condensate[J].Chin.Phys.Lett.2007,24: 616-619.
[10]F.Chevy,V.Bretin,P.Rosenbusch,K.W.Madison,and J.Dalibard.The transverse breathingmode ofan elongated Bose-Einstein condensate[J]. Phys.Rev.Lett,2002,88:250402-250405.
[11]D.S.Jin,M.R.Matthews,J.R.Ensher,C.E.Wieman,and E.A.Cornell.Temperature-Dependent Damping and Frequency Shifts in Collective Excitationsofa Dilute Bose-Einstein Condensate[J].Phys.Rev.Lett,1997,78:764-767.
[12]M.Guilleumasand L.P.Pitaevskii.Temperature-induced resonances and Landau damping of collectivemodes in Bose-Einstein condensed gases in spherical traps[J].Phys.Rev.A,1999,61:013602(1)-013602(10).
Landau Dam p ing and Frequency-shift of Breathing M ode in a Spherical Bose-Einstein Condensate
MA Rui,FU Yu-dong,MA Xiao-dong
(CollegeofPhysicsand Electronic Engineering,Xinjiang NormalUniversity,Urumqi,Xinjiang,830054,China)
The Landau damping and frequency-shiftof three low-energy breathingmode in a spherical Bose-Einstein condensate are investigated by using themean-field theory approximation.The damping rate and frequency-shiftmagnitude and their temperature dependence are analytically calculated in order to provide the certain reference value for theoreticaland experimental research.
Bose-Einstein condensate;Damping rate and Frequency-shift;Hartree-Fock-Bogoliubov approximation;Thomas-Fermi-Approximation
O469
A
1008-9659(2016)02-0045-06
2016-02-01
国家自然科学基金项目(11264039)。
马 瑞(1989-),男,新疆阜康人,硕士研究生,主要从事理论物理研究。
*[通讯作者]马晓栋(1964-),男,山东菏泽人,教授,博士,主要从事统计与凝聚态理论研究。
