基于追踪数据的全球中尺度涡旋偶极子自动识别方法

田丰林，苑忠浩，刘巍，程领骑，陈戈,2*

( 1.中国海洋大学 信息科学与工程学院，山东 青岛 266100；2.青岛海洋科学与技术试点国家实验室，山东 青岛 266237；3.自然资源部城市国土资源监测与仿真重点实验室，广东 深圳 518034；4.青岛市计量技术研究院，山东 青岛 266100)

1 引言

中尺度涡旋是一种广泛存在于海洋中的环形水流，它们的尺度通常超过数十至数百千米，影响时间持续数十至数百天，并且它们对全球海洋中的热、盐和生物化学物质的传播和平衡发挥着重要作用[1]。对于海洋中存在的数千个涡旋，可以分为气旋涡(Cyclonic Eddy, CE)和反气旋涡 (Anticyclonic Eddy, AE)[2]。此外，如果把涡旋的彼此关系考虑进来，海洋中还存在许多偶极子的结构，它们由一个气旋涡和一个反气旋涡组成。偶极子在海洋中很常见，特别是在海洋东边界附近[3]或者是西边界流有关地区[4]。有证据显示在卡迪兹湾地区存在许多间歇性的水面以下的偶极子[5]。最近发现的一项研究表明存在一些偶极子在南极绕极流（Antarctic Circumpolar Current， ACC）地区以10倍于罗斯贝（Rossby）波的速度传播[6]。

随着观测手段的发展，目前积累的1993年1月至2016年9月间的卫星高度计数据使我们能够进行大尺度和长时间序列的中尺度涡偶极子的研究，此外，卫星还提供了海面温度异常、海面盐度异常数据辅助探究偶极子。这些海量的数据（数十TB）一方面为研究偶极子提供了更多的数据支持，另一方面也对计算效率提出了更高的要求，传统的人工识别方法需要通过目视观测[6]，工作量巨大，识别结果具有较大的主观性，并且难以有效地利用已有的遥感数据集，亟须提出新的自动识别算法。

为了高效地识别全球偶极子，本文提出了一种基于涡旋追踪数据的全球自动偶极子识别算法。偶极子是描述涡旋间关系的一种模式，是两个涡旋相互结合形成的新的拓扑结构[6]，目前针对单个涡旋的研究相对较多，但针对多个涡旋间关系的研究相对较少，特别是偶极子模式，当前的研究并没有完全揭示这种结构在海洋中的分布规律，也没有充分解释偶极子和单个涡旋之间的内在的客观联系；同时偶极子是一种内部相对稳定的结构，彼此之间一定程度上相互独立的影响着海洋环境；涡旋以偶极子的形式参与到能量和物质运输[7]，两者是个体与整体的关系，但作为一个整体它在能量、温度和盐度等方面的影响将会产生新的变化[4]；因此需要对偶极子的特性进行单独的统计分析。通过对累计23年的涡旋追踪数据的处理和计算，本文共发现了超过10万对偶极子，并且发现在全球海洋的不同区域偶极子具有不同的传播和演变特征。本文对这些偶极子轨迹的演变模式进行了分类和分析，并利用海表面温度异常（Sea Surface Temperature Anomaly, SSTA）和海表盐度异常（Sea Surface Salinity Anomally, SSSA）验证了典型偶极子的存在。

本文的剩余部分组织如下：在第二节简要总结了前期相关工作和成果后，在第三节提出全球偶极子的自动识别提取方法，并在第四节展示了全球识别结果。在第五节，本文分别介绍伴随时间长、传播速度快和纠缠传播的偶极子特征，并通过叠加SSSA和SSTA背景数据来验证它们的存在。最后，对本文进行了简要总结，并描述了未来的研究方向。

2 相关工作

目前，国际上针对偶极子模式的研究主要集中在局部区域或者少数几个轨迹。Apango-Figueroa等[7]针对加利福尼亚南部湾中尺度偶极子的三维分布进行了分析，研究了偶极子对生物指标的影响。Carton等[8]报告了在圣文森顿角西南部发现和采样的两个中尺度涡旋的演变，这两个涡旋短暂的相互作用并发展，然后分离，遵循不同的轨迹继续传播。Hooker等[4]通过对海达–格瓦伊南端圣詹姆斯角潮流的数值模拟，发现了一些中尺度偶极子是由潮汐涡旋周期性合并而成的。Davies等[9]研究了位于加利福尼亚湾的涡旋偶极子，通过从多普勒海流剖面仪获得的速度剖面数据和从配备多种传感器的温盐深剖面仪探头得到了许多垂直剖面特性数据，并分析了偶极子幼鱼栖息地的影响。de Ruijter等[10]利用TP/ERS卫星高度计数据，在马达加斯加东南部发现了17对偶极子模式，这些涡旋携带大量马达加斯加暖流的水注入阿古拉斯回流区，并且在莫桑比克海盆区域变得不稳定，然后发生多次分裂与合并，这些涡旋对的产生具有较强的周期性，并且与印度洋偶极子和厄尔尼诺现象之间存着年际关联。

在国内，有关南海以及印度洋等海域的偶极子模式研究比较多。Chu等[11]研究了南海的厄尔尼诺-南方涛动 (El Niño–Southern Oscillation, ENSO)和涡旋偶极子的关系，并发现了ENSO对于偶极子产生的促进作用。樊孝鹏等[12]通过对南海卫星高度计数据进行希尔伯特–黄变换得到了海平面高度变化的能量频率时间谱，并发现了一对中心分别位于海南岛和吕宋岛周围海域的随季节变化的偶极子模式。陈符森等[13]借助多年海面高度异常（Sea Level Anomaly, SLA）数据进一步研究了南海海域涡动能比，发现了AE和CE交错分布在南海东部，越南东部涡旋呈偶极子分布，且具有季节性变化。杨秋明[14]通过对南印度洋多年的海温资料进行主成分分析得到了海温主要模态，结合中国降水观测数据，发现了南印度洋副热带偶极子型海温异常强度和春季华北地区降水状况的潜在关联。徐海明等[15]进一步总结了南印度洋偶极子气候变化的影响，指出它能够影响热带和热带外大气环流。

总体上目前的研究主要集中在局部范围内的偶极子特征，针对全球范围内的偶极子的识别和分析很少出现。采用的识别方法主要为人工判别，主观性较大，并且由于海洋数据的体量巨大，计算任务非常复杂，随着观测手段的不断提升，这种矛盾会进一步的增加，提出能够自动识别偶极子的算法的重要性日益突出。

3 偶极子自动识别方法

3.1 涡旋识别与追踪

目前已经存在许多涡旋自动识别算法，这些算法可以分为3类：（1）基于物理参数的方法，包括Okubo–Weiss参数法[16]，基于缠绕角度的方法[17–18]和小波分析法[19]；（2）基于流向的方法[20]；（3）基于海洋高度数据的方法[21–22]。除此之外，还有一种基于拉格朗日的现代方法[23–24]也被提出来用于确定在湍流中的涡旋结构。

涡旋轨迹的追踪方法主要有两大类。第一类追踪方法被称为基于相似性的方法。Penven 等[25]首次使用无量纲的欧几里涡流特征距离来描述两组连续高度计数据中的涡旋相似性，该方法及其改进版本已经被广泛应用于全球中尺度涡追踪[26–27]。第二种被广泛应用的涡旋轨迹追踪算法是由Chelton等[21]提出，这种方法包括找到最佳匹配的涡旋，以及在两个连续的时间序列中，使用指定的阈值限制进而进行自动追踪操作。

3.2 相关数据

本文使用的涡旋识别和追踪数据是由Tian等[28]发布的（http://coadc.ouc.edu.cn/tfl/）。该涡旋识别数据是基于空间分辨率为(1/4)°×(1/4)°、时间分辨率为1 d的SLA数据[29]得到，通过海面高度（Sea Surface Height,SSH）法完成涡旋识别，并进行了涡旋轨迹追踪。Chelton等[21]已经证明，基于SSH的方法能够有效避免额外的噪声引入和冗余的涡旋检测，使用基于其他方法识别的涡旋数据进行偶极子模式检测，结果可能存在差异，但本文提出的偶极子模式匹配算法是相对独立的模块。本文使用的从1993年1月到2016年9月期间的追踪数据中有大约超过300万条涡旋轨迹。由于本文采用的SLA数据精度为(1/4)°×(1/4)°，因此通过本文算法识别得到的偶极子涡旋必须满足半径大于(1/4)°，但是本文的提取算法针对不同的分辨率具有良好的自适应性和伸缩性，随着数据精度的提高，得到的识别结果也会得到相应的提升。目前国内外对于偶极子的准确定义随着研究区域的改变仍未统一，为了能够在全球范围内统一地提取偶极子模式，在本文中将其定义为在累计时间I(≥60) d内连续保持共同移动的一对气旋和反气旋涡形成的涡旋对，并且要求两者涡心距离D小于阈值（2.5°（纬度/经度），计算时换算成球面距离），这种定义是对局地不稳定性引发的偶极子现象的扩展，是AE和CE彼此之间形成的新的拓扑关系，它们以一种相对稳定的整体在较长的时间里共同影响海洋环境。这种广义偶极子模式不仅仅分布于特殊地区，因此它的存在和特性会受到罗斯贝波和海水层结效应影响[30]。郑全安等[31]把南海中尺度涡作为群体传播的现象归结为长寿涡列、驻波模态和罗斯贝标准模态3种认识。Xie等[32]进一步针对南海海盆模拟了由AE、CE交替组成的罗斯贝标准模态，并通过SLA数据验证了这一模式的周期性。由于罗斯贝波即是以正负海面高度异常传播的，在海盆内，波动与边界相互作用还会形成固有模态，使得整个海盆内多个棋盘状分布的正负涡旋同步向西移动，在罗斯贝波机制下大多数涡旋在相隔不远处有反极性涡旋是较为常见的[33]，单个中尺度涡一定程度上可以看做非线性罗斯贝波一部分。同时Chelton等[34]也提出在北太平洋纬度小于25°N区域内，检测到的SSH变化符合罗斯贝线性波理论，而在25°N以北区域则主要归因于非线性涡旋信号。本文更关注的是涡旋对的匹配机制，因此并未对不同性质的涡旋信号进行区分。另外，本文使用的SSTA数据来源为美国国家海洋和大气管理局的甚高分辨率扫描辐射计数据(https://www.ncei.noaa.gov/data/)，其数据的空间分辨率精度为 (1/4)°×(1/4)°，时间分辨率为1 d。海表面盐度数据来源于欧空局土壤水分和海洋盐度卫星的海表面盐度L3级产品(http://bec.icm.csic.es/ocean-global-sss/)，由于本文最终使用的是SSSA数据，因此我们以每年海表面盐度数据的平均数据作为该年数据的基准，进而获得了SSSA数据，该数据的空间分辨率精度为 (1/4)°×(1/4)°，时间分辨率为1 d。

3.3 偶极子提取

传统的偶极子涡旋识别方法通常是基于目视解译的，存在较大的局限性，特别是在数据量较大的情况下，这种方法既困难又耗时。针对这一大数据挑战，本文提出了一种基于涡旋追踪数据的自动偶极子提取方法，这种方法由3步组成，如图1a所示。

第一步是数据预处理。原始涡旋追踪数据每一项的结构为与涡旋位置有关的数组，这种结构不适合通过日期进行快速定位涡旋数据。为此我们构建了一个以日期为索引值，以涡旋为实值的字典结构。这个新数据集中的每一项记录了当天的全球涡旋数据。为了方便区分涡旋极性，我们将气旋和反气旋涡旋轨道分别映射到两组这种新的结构中。经过这一处理步骤，将会得到两组记录不同日期的气旋和反气旋涡旋的数据集，便于之后的处理工作。

第二步是涡旋对探测。对于从第一步获得的每一天的全球涡旋数据，我们基于涡旋之间的距离建立K–D树，实现空间分割。在K–D树上新增、删除和最近邻搜索节点，平均复杂度为O(logN)，如果不采用K–D树，每次匹配操作的平均复杂度为O(N)，因此使用K–D树之后，可以实现涡旋数据的快速定位和匹配。K–D树算法已经在海洋领域得到了许多应用。为了能够快速检索数据块，陈秋等[35]在构建高精度数字水深模型中利用了格网树和K–D树结合的方式，提升了检索效率；Tian等[28]和Sun等[36]在涡旋追踪过程中也通过引入K–D树算法加快涡旋匹配追踪；Lynch等[37]将这种算法应用到了流体模拟过程中从而改进了求解效率。在实际计算过程中，本文使用的计算平台为Win10教育版x64系统，CPU为8核Intel(R) Core(TM) i7-3770K @ 3.50GHz，内存为 16 GB，在不使用K–D树的情况下，完成23年数据的计算大约需要16.09 h，而经过K–D树优化之后，只需722.64 s即可完成全部数据的计算，效率提升了80多倍。

基于上述过程建立的K–D树，我们在一定距离D内搜索每个气旋涡周围的反气旋涡，建立一个新的数据结构：涡旋对 (AE，CE，T)，AE 和 CE 分别表示反气旋涡和气旋涡，T用于记录涡旋对的累计伴随时间，初始化为1。由于这种轨迹匹配过程可能中间出现若干天的丢失现象，导致记录的涡旋对出现临时性的中断，但当它们再次出现时，T的记录将会保留上次的结果，而不是作为新的涡旋对记录。因此，T可以用来表示两个涡旋轨迹在一定距离内累计相伴的时间。在最终的结果提取时，本文只保留那些相伴时间超过60 d的涡旋对。以图1b至图1e为例，涡旋A和B在不同时间点如果被判断为最接近并且距离小于D，那么TAB就会增加1，匹配过程中如果A和B间的距离不再满足条件时，TAB并不会清零（如图1b所示），当条件再次符合时，将会继续累加计数。如果最终TAB大于最低伴随天数的阈值，那么A和B将会被判定为一对稳定的涡旋对。

第三步是偶极子轨迹提取。本文算法将会跟踪涡旋追踪数据中的每个涡旋对结构(AE，CE，T)，并计算出各涡旋对的最大传播速度和平均传播速度，同时还可以得到传播距离和伴随寿命等特性，并将其保存为涡旋对的特征值。对于每个特征值，本文算法可以通过设置阈值来过滤涡旋对，最终保留下来的涡旋对结果将被作为偶极子识别结果存储出来。Hughes和Miller[6]认为偶极子模式是理论上预测的例外，它可以以远大于罗斯贝波速的速度将水输送到东部或西部，导致热量和营养等的异常传输。但关于相关筛选的阈值如何设定目前还没有确切的定论，随着相关理论的发展，可以进一步改进本文算法，以支持更加精细化的特定偶极子模式识别。

图1 偶极子模式提取算法Fig.1 Recognition algorithm of global mesoscale dipole

4 偶极子识别结果

本文根据已有1 616 191条气旋涡轨迹和1 589 949条反气旋涡轨迹，总共发现有向东传播的30 590对偶极子和向西传播的86 662对偶极子，并获得了全球偶极子轨迹。图2a中红色和蓝色轨迹线分别代表向东和向西移动的偶极子的所有轨迹，这些组成偶极子的两个涡旋在2.5°范围内保持一定距离共同移动超过60 d时间。向东移动的偶极子大部分分布在ACC地区，部分分布在北太平洋(North Pacific Ocean, NPO)和北大西洋(North Atlantic Ocean, NAO)地区（图2b），可以发现向东移动的偶极子集中分布在高纬度地区，这应该与活跃在这些地区的较强的东向洋流活动有关。另一方面，向西移动的偶极子主要分布在赤道两侧，一小部分向西移动的偶极子分布在NPO和NAO地区（图2c）。根据Chelton等[21]的研究，东向传播的涡旋通常分布于南极绕极流、黑潮以及大浅滩等地区，西向传播的涡旋则主要分布在中低纬度地区，本文得到的偶极子识别结果和这一结果基本一致，这说明涡旋活跃地区，更容易发生偶极子的捕获。

基于识别结果，本文进一步分析了偶极子的传播速度特征。图3显示了平均传播速度超过5 km/d的偶极子轨迹。如图3a所示，东向快速移动偶极子主要分布在ACC地区，而大多数向西快速移动的偶极子分布在赤道两侧（图3b）。通过与全球涡旋轨迹图像（图3c，图3d）的对比，可以发现偶极子数量主要在黑潮地区以及阿拉斯加湾等地区相对于涡旋轨迹数量明显减少，这可能与近大陆的地形分布以及洋流活动有关。这些地区具有较强的流场，涡旋和流场、涡旋和涡旋之间的相互作用次数增加，能量消散的速度变快，导致涡旋生命期减短[38]，偶极子模式的存活期也会相应减短。

图2 通过本文方法提取偶极子轨迹Fig.2 Tracks of dipole extracted by our method

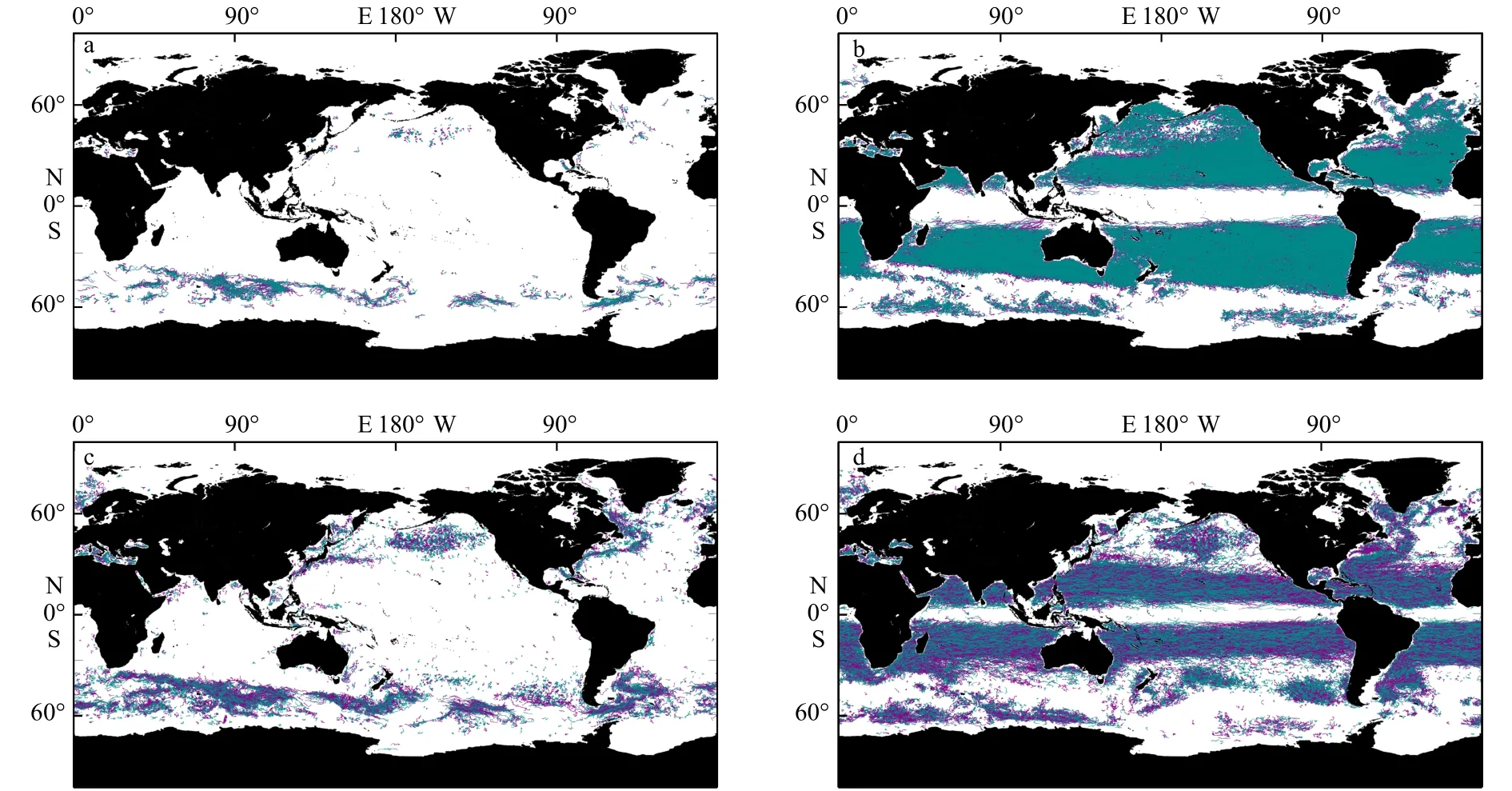
图3 平均传播速度超过5 km/d的偶极子或涡旋轨迹Fig.3 Tracks of dipole or eddy with average speed over 5 km/d

从识别结果中，本文发现了许多偶极子彼此耦合相伴了很长时间。图4显示了彼此伴随超过180 d的偶极子轨迹，其中一共有1 053对向东移动的偶极子和6 294对向西移动的偶极子一起传播超过了6个多月时间。它们通常起源于大洋东岸，在澳大利亚东部和南部、美国东部和非洲东北部，向西移动的长寿命偶极子分布非常广泛。然而，除了ACC地区之外，几乎没有长寿命的偶极子向东移动。

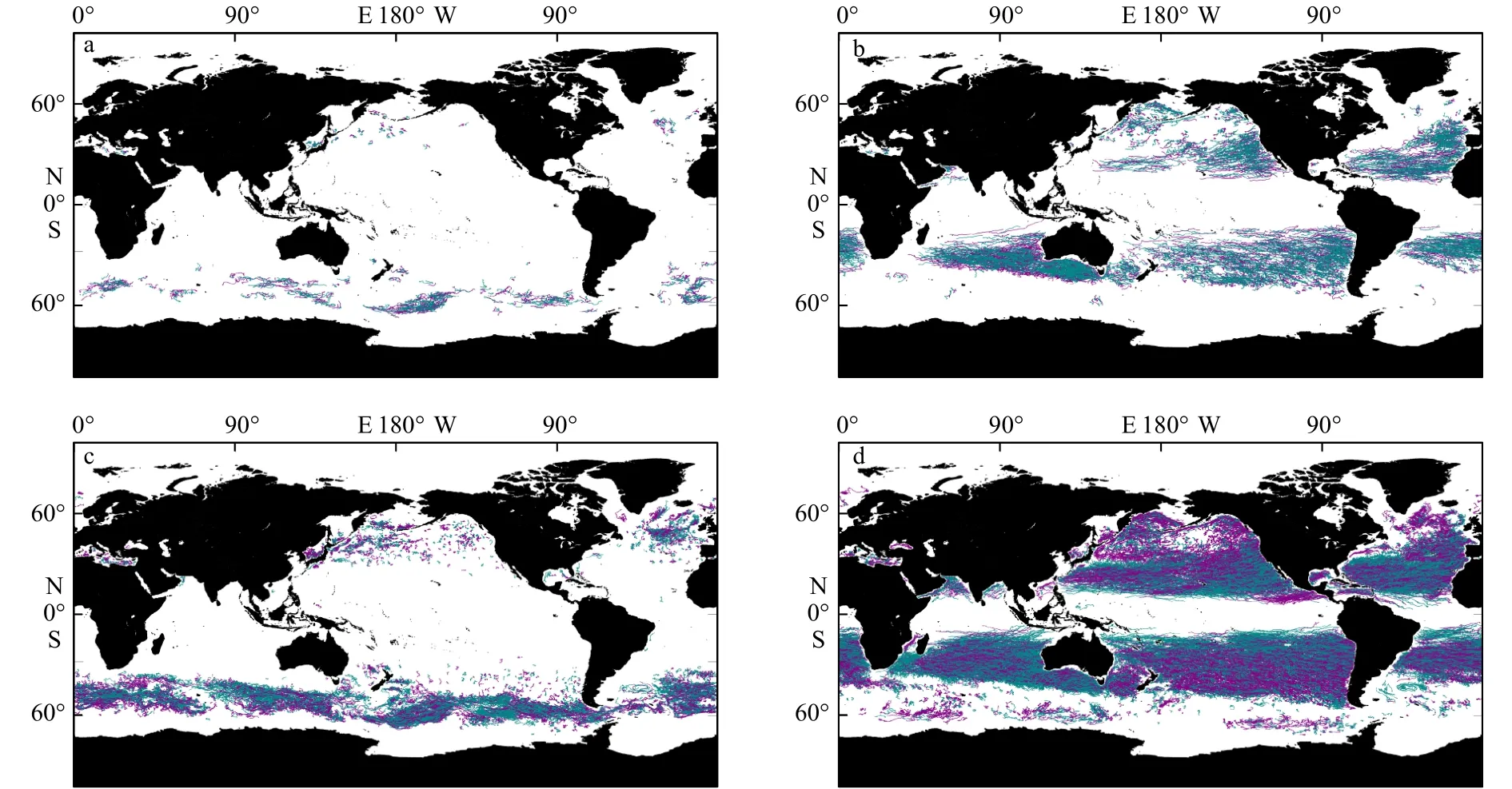
图4 伴随时间超过180 d的偶极子或寿命超过180 d的涡旋的传播轨迹Fig.4 Tracks of dipole or eddy that existed for over 180 days

5 偶极子验证及传播模式分析

在本节中，将针对全球海洋不同区域的偶极子做进一步的研究，分别提取并分析具有长时间伴随、传播速度快和纠缠传播特点的偶极子轨迹，具有这些传播特点的涡旋已经得到了前人的研究[21]，本文主要结合SSTA和SSSA分布情况，分析由偶极子的运动引发的温度异常和盐度异常，并验证偶极子的存在。在前人研究[39]的启发下，为了直观地观察偶极子结构，本文定义了以偶极子两个涡心的中间位置为图像中心的坐标系，通过使用SSTA和SSSA数据绘制偶极子图，得到了平均偶极子结构。

5.1 长时间伴随

根据本文算法得到的全球偶极子的平均伴随时间为92.09 d，且大部分的伴随时间分布于60～150 d之间。

图5a显示了1993–2016年间伴随时间超过60 d的117 252对偶极子首次捕获的位置分布，可以发现偶极子首次捕获的位置倾向于分布在西海岸地区，这与图2全球偶极子的分布规律是相吻合的。把伴随时间超过200 d的2 290对偶极子单独计算时（图5b），发现它们大部分集中分布在中纬度地区，在赤道附近几乎没有长时间伴随的偶极子诞生，这一点也与涡旋在低纬度地区的寿命较短的规律吻合。

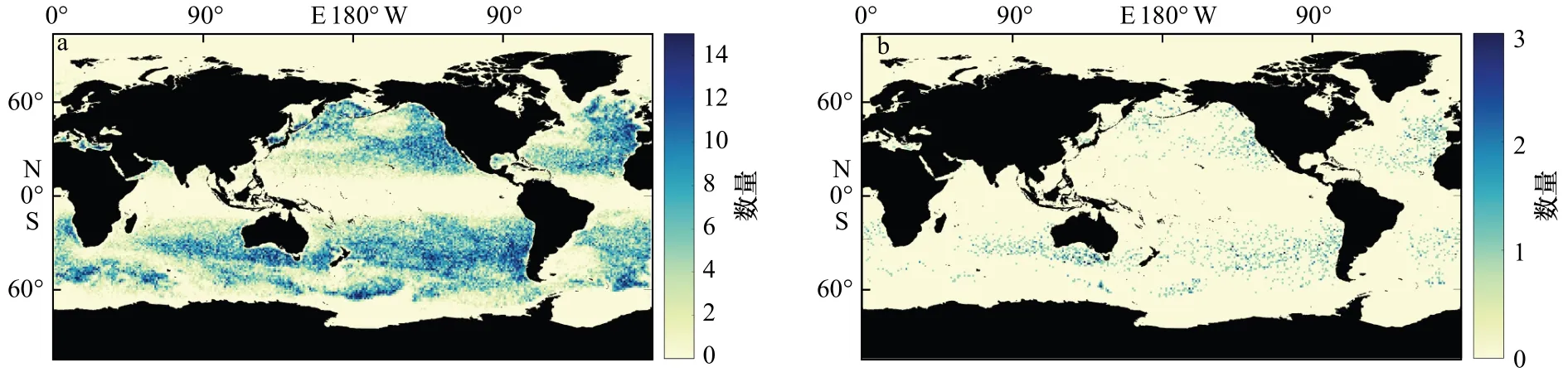
图5 以偶极子的中心(取气旋涡和反气旋涡的两个涡心的中间位置)进行统计，伴随时间超过60 d的偶极子的首次捕获的位置(a)和伴随时间超过200 d的偶极子的首次捕获位置(b)Fig.5 The center of the dipole pairs (the middle position of the two vortex center of the anticyclonic eddy and cyclonic eddy) was counted, the first capture position of dipole pairs that existed over 60 days (a) and the first capture position of dipole pairs that existed over 200 days (b)

为了更清楚地研究伴随时间长的偶极子特点，并验证偶极子的真实性，本文选取了一条传播时间长的偶极子轨迹，并结合相应的温盐数据，进行了分析。图6a显示了南美洲西海岸的一对向西移动的偶极子，这对偶极子的传播过程中的SLA图像为图1b至图1e。最初，AE在72°W附近产生，并在此短暂停留一段时间后向西传播。2014年12月28日，当到达76°W时，它和一个新诞生的CE相互吸引，随后共同向西偏北方向传播，两者几乎呈平行移动，直到2016年3月21日，在93°W附近随着CE的死亡，两者作为偶极子的模式破裂。随后AE又继续传播了一段时间后也消失。两者总共伴随了450 d，平均传播速度为4.07 km/d。图6b至图6e为不同时间这对偶极子的局部识别结果，背景为SSTA数据，可以看到这对偶极子在传播过程中对周围环境的影响，从而验证了这对偶极子的真实存在。

本文利用SSTA数据，通过转换坐标系，并进行归一化处理，得到了平均偶极子结构(图6f)，图中坐标表示归一化后的大小，无实际量纲。图6f展示的为偶极子传播过程中平均温度异常，图像中的3个加大的点从上到下依次为归一化后的AE中心，偶极子中心和CE中心。可以明显的发现由于这对偶极子的传播，反气旋涡中心周围区域形成了一个高温异常，气旋涡中心周围区域形成了一个低温异常，图上的两个温度异常中心并没有与两个涡心完美的重合，这可能是由于偶极子传播过程中会对周围水域存在搅拌效应，导致两个异常区域中心相对于涡心位置发生了一定程度的偏移。为了进一步的验证这一结果，本文将2010年至2016年9月的传播时间超过200 d的共计598对偶极子的归一化结果进行了叠加，得到的结果如图6g所示，可以看到经过多年数据的叠加，平均偶极子结构更加稳定，进而验证了这些涡旋以偶极子的形式参与了全球海洋的温盐平衡，并且经过叠加的归一化数据的数值都小于单个偶极子归一化后的结果。

图6 偶极子涡旋传播轨迹(a)；偶极子在不同日期的涡旋识别结果(b−e)；偶极子周围的平均温度异常(f)；多年数据叠加后的偶极子平均温度异常(g)Fig.6 Positions of the dipole eddy core during their life time (a), eddy detecting result of the dipole at different days with background of SSTA (b−e), the average SSTA anomalies around the dipole (f); the average superimposed SSTA around dipoles (g)

图7展示了这对偶极子在传播过程中，作为其组成的CE和AE的最大地转流速度变化特征。可以发现在该偶极子传播过程中，速度比值基本稳定在1附近，但整体AE的传播速度稍微强势一点，平均传播速度比值为 1.06（AE/CE）。

5.2 快速传播的偶极子

本文定义偶极子传播速度为其传播距离与整个生命长度的比值，基于此定义，针对所有偶极子的传播速度进行了统计分析，得到结果如图8a所示。全部偶极子的平均传播速度为 3.85 km/d，大部分的传播速度为3～5 km/d，并且速度分布呈现出明显的拖尾现象，统计中最快的传播速度甚至达到了15 km/d以上。

为了更好地分析生命周期和传播速度的关系，我们将传播速度与生命周期长度的变化做了一个相关性分析，结果如图8b所示。图中的红线为本文做的对数拟合的结果，由于参与运算的偶极子的时间阈值为60 d，因此0～60 d部分的数据为0，但是考虑到伴随时间短的偶极子准确性不高，因此去除这一部分之后的数据结果依然可以是可信的。通过图像可以发现随着伴随时间的增长，传播速度整体呈现对数下降的趋势。

本文将传播速度超过5 km/d的17 990对偶极子的首次捕获位置进行统计，得到了图9a，可以发现对于传播速度快的偶极子，大部分起源于低纬度地区，并且大部分位于纬度10°～30°之间，在赤道附近以及中高纬度地区很少有传播速度较快的偶极子，这种分布和高速移动的涡旋分布是相似的，这可能是受到罗斯贝波和重力波的影响。本文进一步统计了传播速度超过10 km/d的偶极子模式，总共发现了466对偶极子，其中只有17对的伴随时间超过了100 d。

本文专门选取了其中一个较为典型的快速传播偶极子进行分析，它的传播轨迹如图9b所示。2010年12月10日，CE在39.8°W附近和一个AE组成偶极子结构，开始共同向东传播；之后发生了一次转向，在最东达到了 36.5°W 之后，两者相伴向西传播，并在传播过程中发生了一次相对位置的互换，最终在2011年3月24日两者彼此分离，随后消失。这对偶极子总共伴随105 d，平均传播速度为11.84 km/d。本文为了验证这对偶极子在传播过程中对周围环境的影响，利用SSSA数据对它们生命期内的盐度背景场进行归一化处理，得到了对应的SSSA结构（图9c），这一结构和5.1节中归一化温度结果比较相似，在气旋涡和反气旋涡的涡心周围分别形成了高盐和低盐异常区域，同时由于偶极子水体的搅拌作用，这两个中心也相对于涡心存在不同程度的偏移。为了减少偶然因素的影响，本文将2010年至2016年9月的传播速度超过10 km/d的偶极子（共计413对）归一化结果进行叠加，得到了图9d，与图6g结构相比，偶极子海洋盐度影响的平均结果似乎变得相对不稳定，但在中心位置偶极子模式依然较为明显的引起了海洋盐度的变化。

图7 一对偶极子传播过程中最大地转流速度变化（a）和对比（b）Fig.7 The changes (a) and comparisones (b) of the maximum geostrophic velocity of a dipole

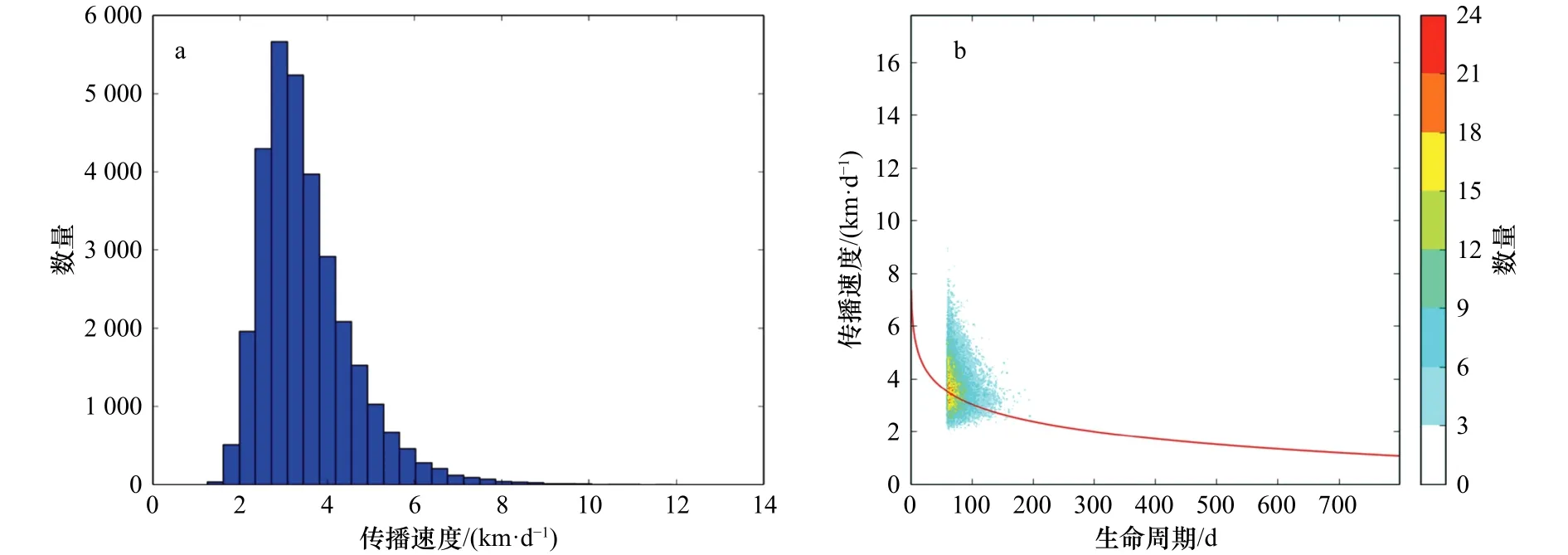
图8 偶极子传播速度的分布(a)和偶极子传播速度与生命周期的对应关系(b)Fig.8 Distribution of the propagation velocity of dipole pairs (a), and the corresponding relationship between the propagation speed of dipole pairs and the life cycle (b)

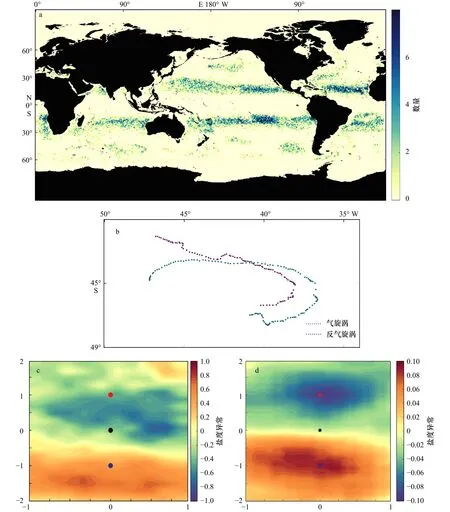
图9 传播速度快(≥5 km/d)的偶极子首次捕获位置的全球分布(a)；偶极子的传播轨迹(b)；偶极子周围的平均盐度异常(c)；多年数据叠加后的偶极子周围的平均盐度异常(d)Fig.9 The first capture position of dipoles with fast propagation speed (≥5 km/d) (a); the selected dipole’s tajectory (b); the averageSSSA around the selected dipole (c); the average superimposed SSSA around dipoles (d)

5.3 纠缠传播的偶极子

本文将作为偶极子组成的两个涡旋彼此轨迹发生了交叉的现象称为纠缠传播；并将纠缠角度定义为：以AE为中心，在整个伴随时期内，CE相对于AE的坐标方位角变化范围为[a,b]，则b–a代表这对涡旋的缠绕角度，它表示的是在生命期内CE相对旋转的最大范围。Manucharyan和Jimmermans[40]指出，假定偶极子传播过程中两个涡心距离保持不变，两个涡旋在伴随前进过程中，如果彼此的传播速度不同，那么两者将作为一个整体进行一个超大半径的圆弧运动，也可能是相对的旋转。为了能够更加清楚地表示出这种缠绕关系，本文定义了新的坐标系：以AE作为参考，以CE相对于参考涡旋AE的位置变化作为偶极子轨迹缠绕关系描述。经过这种坐标转换，本文将新的偶极子轨迹重新全部叠加得到了图10的轨迹数量分布图。转换坐标系后，新的轨迹大部分分布在以AE为原点的2.5°（纬度/经度）范围之内，这和本文选择2.5°（纬度/经度）作为偶极子判别阈值是一致的；同时在距离原点小于1°（纬度/经度）的区域内也几乎没有偶极子轨迹的存在，这是受到了本文采用的SSH数据精度限制。距离原点1.5°～2°（纬度/经度）之间的区域有着最丰富的偶极子轨迹分布，同时可以发现在纬向方向上偶极子轨迹分布的密度更大，而在经向方向上偶极子轨迹较为稀疏，并且密度分布呈现出纬向条带状，这可能与偶极子东西向传播占优有关[21]。

图10 以反气旋为原点，全球偶极子轨迹叠加示意图Fig.10 Superposition of global dipole trajectories with anticyclone as the origin of coordinates

经过分析后本文发现，大部分的偶极子所做的纠缠运动的角度都相对较小，平均的缠绕角度为41.3°，这与偶极子各个组成部分具有相近的传播速度的现象吻合。但是，仍然存在许多偶极子具有较大的缠绕角度，本文选取了伴随过程中缠绕角度超过90°的纠缠传播偶极子作为典型纠缠传播偶极子进行研究，并总共得到了8 528对伴随时间超过60 d的轨迹，结果如图11a所示。本文选择了其中一个典型的纠缠传播偶极子进行研究分析，其传播轨迹如图11b所示，它们一同向西南传播，在传播过程中两者并没有保持相对平行的传播。相反，CE和AE在传播过程中相互纠缠，并且发生多次位置交换。2015年11月8日CE首先诞生，在它先向南移动几天后，2015年12月7日AE出现在它的南部，随后二者相互吸引，并共同移动，在伴随过程里CE与AE的相对位置共发生了7次位置交换，缠绕角度达到了167°，最终AE的位置位于CE的北部，并在2016年5月13日两者同时消失。基于SSTA和SSSA数据，可以获得这对偶极子周围影响的归一化结构（图11c至图11d），由于偶极子的彼此缠绕，导致形成的归一化结果相对松散，但仍然可以展现出对温度和盐度的影响。图11e至图11f展示的是2010年到2016年9月期间的缠绕角度超过120°的偶极子(共计858对)归一化的叠加结果，经过多次叠加取均值，有效的降低了单个轨迹的偶然性，偶极子结构更加明显。

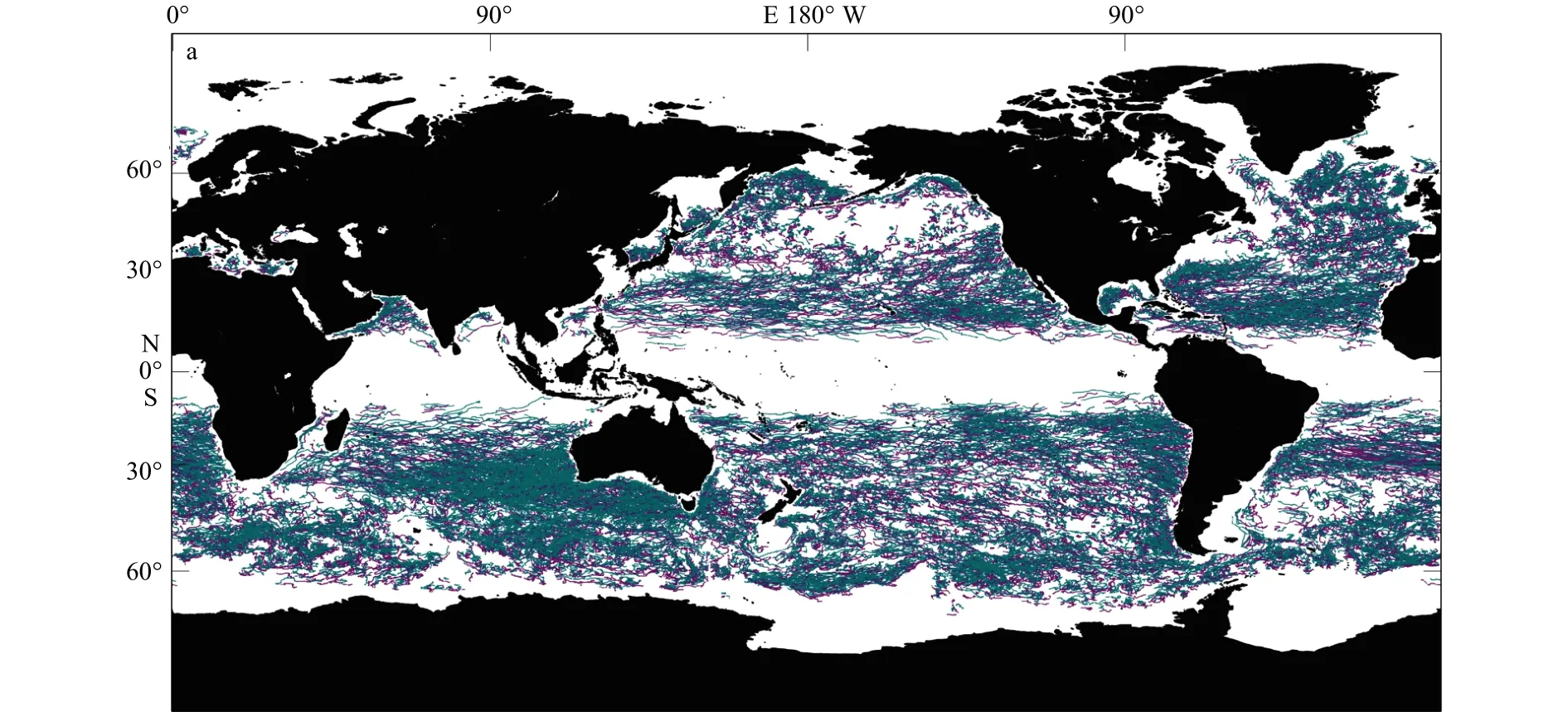
图11 全球纠缠传播偶极子(缠绕角度大于90°)轨迹(a)；选取的纠缠传播的偶极子轨迹(b)；经过归一化后的偶极子数据结构(c−f)选取的偶极子周围的平均温度异常(c)；选取的偶极子周围的平均盐度异常(d)；多年数据叠加后的偶极子周围的平均温度异常(e)；多年数据叠加后的偶极子周围的平均盐度异常(f)。红色粗点代表归一化后AE涡心，蓝色粗点代表归一化后CE涡心Fig.11 Trajectories of tangle dipole (a).The selected dipole’s trajectory (b), blue represents CE,purple represents AE.Nnormalized dipole structure (c)(d)(e)(f), the red dot represents the normalized AE core, and the blue dot represents the normalized CE core.The average SSTA around the selected dipole (c).The average SSSA around the selected dipole (d).The average superimposed SSTA around dipoles(e).The average superimposed SSSA around dipoles (f)

6 结语

本文主要围绕全球范围内偶极子的识别提出了一种高效的自动化提取算法。如果两个涡旋间存在偶极子模式，那么它们应当在较长的时间内保持较近的距离共同传播。本文使用距离指标衡量涡旋之间的紧密程度，使用累积伴随时间指标衡量匹配的稳定性，借助于K-D树的空间索引效率，可以在12 min左右完成23年间涡旋数据的匹配过程。对于匹配得到的涡旋对，可以计算其相关传播特性，并可以通过设置阈值的方式进行筛选。利用该算法对1993—2016年间的涡旋轨迹数据进行了处理和计算，本文总共得到了超过10万对偶极子轨迹。随后本文根据偶极子识别结果，分别分析了具有伴随时间长、传播度速度快和纠缠传播特点偶极子的传播特性，并通过SSTA和SSSA数据对结果进行了验证。通过对典型偶极子模式的归一化统计，本文发现偶极子在传播过程中以相对稳定的整体对周围水域的海洋环境产生了较大的影响，验证了涡旋以偶极子的形式参与了全球海洋生物化学环境的平衡与发展。

本文提取的偶极子是对局部区域偶极子模式概念上的拓展，其分布将不会局限于某些特殊地区，这也导致其特性将会受到背景流场和层结场的影响。因此这种算法主要是提供了一种标准化的偶极子提取方法的框架，其中的各项参数仍需要做进一步调整和完善，比如通过要求传播速度远超罗斯贝波速的速度[6]，可以有效的避免罗斯贝波引发的正反涡旋相间排布的冗余判断，而相关参数的确定需要进一步的研究并反作用于本算法。由于海洋环境的复杂性，对于偶极子的研究必须考虑其具体所处的地形与海洋环境，才能够更加细化的解释偶极子模式的外在表征和内在机理，针对不同区域的基于不同成因的偶极子模式识别，是下一步研究的重要课题。

偶极子是气旋涡和反气旋涡彼此吸引捕获形成的海洋特殊现象，它是描述涡旋间关系的一种方式，我们推测不同偶极子在海洋传播过程中也有可能存在聚集效益并捕获，从而构成一个更大集群，并且本文在偶极子识别和分析过程中，发现存在单个涡旋与多个涡旋出现伴随传播的现象，说明多个涡旋之间也可能存在着吸引效应。研究这些彼此吸引的多个涡旋能够更加深入地揭示海洋中的物质能量运输机制，这些现象与课题需要未来进一步的探讨。基于本文算法，我们同样得到了一些南海区域的偶极子模式，将该结果与以往研究[12–13]的对比以及针对南海海域做更加深入的研究，也是我们未来工作的一个重点和热点。