广义不确定性原理对量子跃迁能谱的修正
2016-07-26滕晶贵州大学理学院贵州贵阳550025
滕晶(贵州大学 理学院,贵州 贵阳 550025)
广义不确定性原理对量子跃迁能谱的修正
滕晶
(贵州大学 理学院,贵州 贵阳 550025)
摘 要:在现代物理学中,人们越来越重视精细化研究,对理论与实验间存在的误差产生了浓厚的兴趣.尤其是在量子力学中,人们发现通过理论计算出来的能量总是与实验结果有些许偏颇.那么究竟是理论不够完善还是实验不够精确呢?在此背景下,前人提出了广义不确定性原理,本文基于广义不确定原理,针对重力场中的量子跃迁的能谱进行研究,期望能够获得在该条件下能量的修正,并对此作出物理上的解释.
关键词:量子力学;广义不确定性原理;量子跃迁
近代物理学中,有一些极为有名的理论,如:弦理论、黑洞理论、圈量子引力理论,这些理论看似天差地别,但是他们却有一个共性——可以自然推出最小长度和最大动量的存在.这两个基本存在不仅在物理学中广泛存在,而且对非对易几何也有颇深的影响.在此背景下,广义不确定性原理应运而生[1-8].那么究竟什么是广义不确定性原理呢?简单说来,广义不确定原理修改了海森堡不确定性原理的表达式,即在原先的表达式中加入了参数α.若是修正后的海森堡不确定性关系式能够更好的减少理论与实验间的误差,那么就认为该修正是正确的,有意义的.
那么如何将参数α融入到海森堡不确定性原理的式子中成为了研究者的一个难题,在2012年以前,最为著名的表达式为[9-10]:

前人在此表达式下已经有许多建设性的结论,这些结论在一定程度上拉近了实验与理论间的距离.但是遗憾的是,该表达式在本质上却有着自身无法克服的困难.
●由于该提议本身来源于微扰,继而只对较小量有较好的可用性.
●虽然最小长度与理论本身不相悖,但是其最大动量与DSR理论中的最大动量并不相同.换而言之,该表达式仅给出可测量动量的上界,却不是可观测的动量的值.
在此背景下,2012年,伊朗著名学者Pouria Pedram提出了一个全新的广义不确定原理关系式,该关系式较好的克服了之前遗留下来的两个问题,并且该学者在这一领域的研究颇有建树.本文在他提出的全新的广义不确定原理下,探究广义不确定性原理对量子跃迁的能谱所产生的影响.
1 广义不确定性原理
经典的广义不确定性原理关系式如式(1)所示,基础该原理,之前的学者得到其最小长度与最大动量为:

但是就像引言中所陈述的,虽然该原理从一定程度上解决了一些问题,然而该原理本身却有着一定的局限性.为了克服这些困难,我们采用下面这个全新的广义不确定性式子.

α—广义不确定性原理参数,无量纲
Mp—是普朗克质量
α0—无量纲的广义不确定原理参数

根据上面广义不确定性关系的式子,得到式(5):

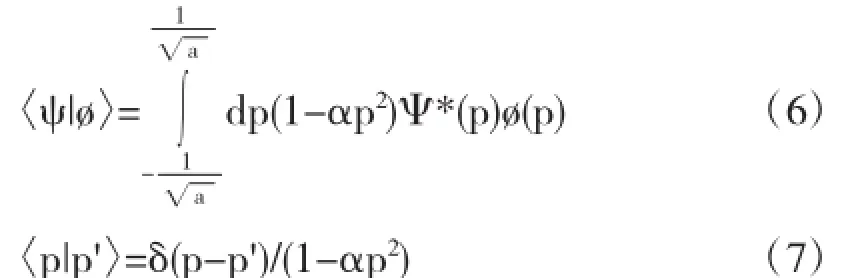
在坐标表象中,坐标与动量又可以表示为如下的式子:
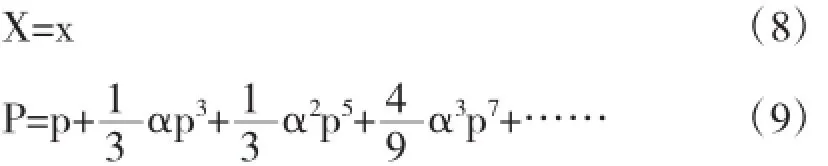
2 广义不确定原理对量子跃迁能谱的修正
研究广义不确定性原理对量子跃迁的能谱修正,首先我们假定一个质量为m的粒子,该粒子处于重力场中,即:

上式中g为重力加速度,在这个体系中,哈密顿量为:

利用等式(9),将修正后的动量表达式带入该哈密顿量,得到:




等式中的ø(p)即为ψ(x)的傅立叶逆变换.对于一个一阶微分方程,我们得到它的解为:

由于广义不确定性原理参数a本身是一个小量,我们可以将上式写成如下形式:

现在,我们运用傅立叶变换,将上式写成坐标表象中的形式:



最后,根据我们预设的条件,在x≤0时,势能为无穷大,因此在x=0处波函数为0.该条件使得能量变成量子化,等式变为:
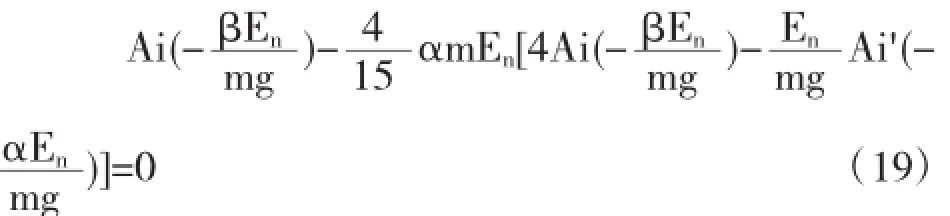
为了进一步研究和计算方便,在这里,我们将一些常量赋值,即g=2ħ=4m=2,赋值之后,等式将大大简化为一个代数等式,能量的本征值即为以下代数式的解:

综上,能量将变为量子化,并且可以从以下波函数中求得.

这之中,En需满足是等式(20)的解.表(1)中作者列举了在广义不确定性原理下前十个激发态能量的修正,从表上我们发现,每一个激发态的能量值均相对增加.

n α=0 α=0.1 α=0.2 0 2.338 2.427 5.570 1 4.088 4.379 4.647 2 5.521 5.948 6.109 3 6.787 7.255 7.353 4 7.944 8.421 8.484 5 9.023 9.493 9.537 6 10.040 10.501 10.534 7 11.008 11.454 11.483 8 11.936 12.370 12.393 9 12.829 13.254 13.271
3 结论
在本文中,我们基于广义不确定性原理,对重力场中的量子跃迁的能谱进行了修正.我们计算了广义不确定原理下的哈密顿量的改变,并且给出了相应的波函数,观察发现,该波函数是一个6阶的微分方程,我们很难得到具体的解析解.因此,在这个背景下,我们将该高阶波函数写成动量表象下的波函数,这种做法很好的规避了上述的困难,在做一个变换之后,呈现在我们眼前的是一个一阶的微分方程.我们在动量空间中得到了该波函数的解,并且得到了在广义不确定原理下的能量的本征值,通过对表(1)中具体的数值分析我们发现,广义不确定原理下的能级相对于之前均有所增加,虽然增加的数值不大,但是却很好的缩小了理论与实验间的误差.在当前的研究中,该修正或许是无足轻重的,但是在日后越加精细化的研究中,广义不确定性下对量子力学的修正必定会变得更为重要!
参考文献:
〔1〕D.Amati,M.Ciafaloniand G.Veneziano, Can space-time be probed below the string Size,Phys.Lett.B 216(1989)41.
〔2〕M.Maggiore,Quantum groups,gravityand the generalized uncertainty principle, Phys.Rew.D 49(1994)5182[hep-th/9305163].
〔3〕K.Nozari,some aspects of plank scale quantum optics,Phys.Lett.B 629(2005)41[hepth/0508078].
〔4〕A.Kempf,G.Mangano and R.B.Mann, Hilbertspace representation ofthe Minimal length uncertainty relation,Phys.Rew.D 52 (1995)1108.
〔5〕S.Hossenfelder et al.,Collider signatures in the planck regime,Phys.Lett.B 575(2003)85[hep-th/0305262].
〔6〕K.Nozari,T.Azizi,some aspects of gravitation quantum mechanics,Gen.Rel.Grav.38 (2006)735.
〔7〕M.Maggiore,A generalized uncertainty principlein quantum gravity,Phys.Lett.B 304 (1993)65[hep-th/9301067].
〔8〕S.Das,E.C.Vagenas,Can.J.Phys.87(2009)233.
〔9〕PouriaPedram,Phys.Lett.B 714(2012)317-323.
〔10〕P.Pedram,Europhys.Lett.89(2010)50008.
〔11〕PouriaPedram,arXiv:1210.5334v [hep -th]19Oct2012.
中图分类号:O413.1
文献标识码:A
文章编号:1673-260X(2016)05-0006-03
收稿日期:2016-03-18
