一种改进的非参数功率谱估计方法
2016-07-26李闰闰武汉工程大学理学院湖北武汉430074
付 敏,李闰闰(武汉工程大学 理学院,湖北 武汉 430074)
一种改进的非参数功率谱估计方法
付 敏,李闰闰
(武汉工程大学 理学院,湖北 武汉 430074)
摘 要:针对功率谱估计方法中的基于离散傅里叶变换的周期图法,提出了改进的非参数化方法中的分段平均周期图法.在信号处理过程中给出宏观功率谱的分析结果,并设计实验进行测试,给出测试情况以及对测试结果的分析.对比经典谱估计方法中的自相关函数估计方法和快速傅立叶变化设计的功率谱分析,改进的非参数化方法更为合理有效.
关键词:周期图法;功率谱估计
针对功率谱估计方法中的基于离散傅里叶变换的周期图法,提出了改进的非参数化方法中的分段平均周期图法.在信号处理过程中给出宏观功率谱的分析结果,并设计实验进行测试,给出测试情况以及对测试结果的分析.对比经典谱估计方法中的自相关函数估计方法和快速傅立叶变化设计的功率谱分析,改进的非参数化方法更为合理有效.
快速傅里叶变换算法在信号领域中得到了广泛的应用,包括谱分析、线性滤波、相关计算等.针对复序列进行频谱分析,得到幅值和相位.
在实际的功率谱的研究中,当幅值的改变不大的时,相位谱的变化却是十分明显的,但是相位的改变并未有十分重大的改变,利用快速傅里叶变换将功率谱表示出来具有实际的重要作用,可以描绘一个信号的实际幅值与相位谱变化.当然在操作过程中由于采样频率的限制会将直接影响信号描述图像的真实程度,但是还是够将信号的变化趋势描绘出来.
1 自相关函数估计法
自相关函数估计法是一种经典的功率谱估计方法,由Blackman和Turkey于1958年提出,故称BT法.

由于x(n)只有N个观测值,因此对于每一个固定延迟m,可以利用的数据只有(N-|m|-1)个,且在[0,N-1]范围内,所以实际计算øxx(m)为
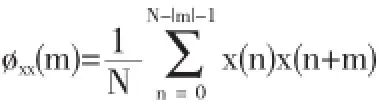
考虑乘积项的长度,自相关序列估计为

式中,m取绝对值是因为øxx(m)=øxx(-m),由于信号的功率谱与相关函数互为傅里叶变换关系,因此,信号的功率谱可以先通过对自相关函数估计,然后按照公式做傅里叶变化得到功率谱估计值.
2 周期图法
周期图法是直接将离散信号x(n)进行傅里叶变换来求取功率谱的估计.设x(n)为有限长随机信号的序列,其功率谱估计可表示为

式中,

即XN(w)是有限长序列x(n)的傅里叶变化.而且XN(w)是成周期性的.直接用XN(w)的模的平方除以N求得功率谱的估计称为周期图,用IN(w)表示为
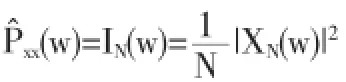
如果x(n)的N个值为x(0),x(1),…x(N-1),则通过快速傅里叶变换可直接求得XN(ejw),再求得(w).这种方法的主要优点是计算简便,它可以直接用FFT算法从x(n)得到XN(ejw),从而得到(w).
利用FFT算法求信号x(t)=sin(2πf1t)+cos(2πf2t)+u(t)的功率谱,其中,f1=40Hz,f2=80Hz,u(t)为白噪声,采样频率fs=1kHz,信号长度去256和1024.

图2-1 功率谱分析
周期图当N→∞时是无偏的,但周期图不满足于一致估计的条件,因此,周期图不是对功率谱最好的估计.对于无限能量的随机序列,其傅里叶变化是不存在的,因此在N→∞的极限情况下是不可能使用的.所以,也就不能期望当N→∞时,IN(w)会等于他的真值(w)而满足一致估计的条件.
3 改进的非参数化方法
为了使周期图满足一致估计的条件,必须将周期图进行平滑处理.而其主要的平滑方法有两种方式,一种是先将数据进行分段,然后再求各段周期图的平均值.这种方法又称为Bartkett的方法.第二种是要选择合适的窗函数作为加权函数进行加权平均来加快收敛的速度.而 Welch和Bartkett的方法进行可以改进,提出用FFT计算的具体方法.

图3-1 改进的非参数方法处理结果
在实际中,功率谱的密度的真值是未知的,但功率谱的窗函数和功率谱密度的一些信息往往是预先知道的.可以通过改变M和L以及利用预先已知的条件,可以更好的选择分段和窗函数.
对信号x(n)进行重叠的分段是平均周期图法.例如按重叠分段,前一段信号和后一段的信号相互重叠一半,这样可以对每一小段的信号序列进行功率谱估计,再取平均值作为整个序列x(n)的功率谱估计,重叠分段的估计曲线一般会更平滑.
4 结论
先用了快速傅立叶变化设计的功率谱的原理进行了理论设计和结果预测,然后应用实际信号进场处理.周期图有个缺点就是频率的分辨率低,周期图发在计算中,把观察到的有限长的N个数据以外的数据都认为是零.这显然是与事实不相符的,从而会导致结果的失真.所以必须要对周期图进行平滑处理,并在改进的非参数频谱估计方法中应用平均周期图的方法,试验结果很理想.
参考文献:
〔1〕康兵,关向雨,舒乃秋,侯铁信,卜正良.几种时频分析方法在VFTO频谱分析中的应用 [J].高电压技术,2015(02):680-686.
〔2〕徐岩,张晓明,王瑜,孙庆彬,王之猛,孙岳.基于离散傅里叶变换的频谱分析新方法 [J].电力系统保护与控制,2011 (11):38-43.
〔3〕吴国乔.全相位方法在频谱分析及数字滤波上的应用[D].天津大学,2006.
〔4〕张登奇,杨慧银.信号的频谱分析及MATLAB实现[J].湖南理工学院学报(自然科学版),2010(03):29-33.
〔5〕丁娜.虚拟频谱分析仪的设计与实现[D].西南交通大学, 2003.
〔6〕何岩峰,吴晓东,韩国庆,肖伟,李伟超,于晓玲.示功图频谱分析新方法[J].石油学报,2008(04):619-624.
〔7〕李振华.基于DSP的频谱分析系统的设计[D].哈尔滨工程大学,2012.
〔8〕何迎迎.信号频谱分析模块设计[D].南京理工大学,2009.
〔9〕祁才君,张圣训.周期信号频谱分析应注意的问题[J].测控技术,1999(04):52-54.
〔10〕王磊.基于频谱和GEMD包络谱分析的旋转机械故障定位研究[D].太原理工大学,2014.
〔11〕才建南.基于BURG法无线电频谱信号的高分辨率估计研究[D].兰州交通大学,2014.
〔12〕罗中良,蓝燕,陈治明.一种频域谱均衡自调整迭代优化算法[J].中山大学学报(自然科学版),2015(05):28-31+ 48.
中图分类号:TP309.7
文献标识码:A
文章编号:1673-260X(2016)05-0017-02
收稿日期:2016-03-05
