棱线强化薄壁方管轴向压溃力学特性

郑玉卿， 朱西产， 胡　强， 陈志宝

(1. 同济大学 汽车学院， 上海 201804； 2. 江西省科学院 应用物理研究所， 江西 南昌 330029)



棱线强化薄壁方管轴向压溃力学特性

郑玉卿1， 朱西产1， 胡强2， 陈志宝2

(1. 同济大学 汽车学院， 上海 201804； 2. 江西省科学院 应用物理研究所， 江西 南昌 330029)

摘要：基于Wierzbicki和Abramowicz提出的方管理想化折叠机构和能量耗散模式，引入棱线与平板的屈服强度比，修正了棱线强化薄壁方管在准静态轴向压溃作用下的能量平衡方程，并推导出了平均压溃力理论预测公式.CAE(computer aided engineering)数值仿真完整再现了稳定压溃阶段棱线强化方管形成一个新折叠单元的塑性变形过程.仿真与理论结果对照表明，理论预测公式可以较准确地预测棱线强化薄壁方管准静态轴向压溃过程的平均压溃力，且最大偏差不超过4.3%；其次，对于截面长、宽、高分别为56, 56,1.0 mm的方管，仅占整个截面周长9.09%的4根强化棱线可使其平均压溃力提升53.8%.

关键词：棱线强化； 折叠单元； 能量耗散； 数值仿真； 平均压溃力

薄壁结构有能力承载超过自身屈曲载荷的变形荷载，也可承受一系列复杂形式的折叠和褶皱变形来实现较大的塑性应变吸能.薄壁梁的轴向压溃力呈上下波动状，力的平均值决定吸能水平，波动范围影响变形的稳定程度，尤其在弯压载荷作用下可通过一定的诱导设计确保其稳定变形[1].方管、矩形管、帽形管等因其结构轴向抗力大且抗弯抗扭性能优越，而被广泛采用并设计成各种形式的碰撞吸能结构件，如汽车前纵梁、门槛梁和前后保险杠吸能盒等.

部分试验研究证实方形管在挤压过程中褶皱长度确实与矩形截面的长宽比无关，但管壁会经历严重的向内和向外塑性弯曲，且必定存有面内拉伸，同时管壁很薄时会发生非紧凑型破损模式，褶皱是不连续的，有发生不稳定的Euler屈曲趋势[2-4]；Meng等[5]利用一系列PVC(polyvinyl chloride)管观察到方管连续变形过程中有瞬间为不动的塑性铰，整个变形过程中四角处初始为垂直的塑性铰，即倾斜移行铰逐渐变成倾斜，最后的倾斜度大约为π/4，还给出了移行铰的能量耗散公式.Wierzbicki等[6]和Abramoowicz等[7]分别基于材料刚塑性假设和动态压缩应变率的估计，描绘了1/4方管截面折叠单元的变形过程并推导了轴向压溃过程力学理论和方管平均压溃力预测公式, 唐治等[8]基于数值仿真和压溃试验研究了矿用防冲折纹薄壁方管构件的轴向压溃性能和吸能特性.上述研究成果均是围绕单一材质方管开展的，然而方管在成形过程中强度各异现象是普遍存在的，至今未见针对强度各异方管在轴向压溃方面的理论探索和报道.

本文拟选取方管为研究对象，采用Ji等[9]给出的帽型结构棱线强化新工艺和部分材料测试数据，仅仅只将受焊接和加工工艺影响较小的方管棱线进行局部超高强化处理，理论推导准静态轴向压溃过程中棱线强化方管的平均压溃力预测公式并进行相应的数值仿真验证，分析棱线强化效果，探究其轴向压溃过程的能量耗散机理和力学特性.

1棱线强化方管吸能特性

1.1基本模型假设

图1为1/4方管准静态压缩吸能分析模型，其中图1a表示1/4方管折叠单元的初始几何形状，图1b表示1/4方管折叠单元准静态轴向压溃时理想化的塑性变形模式，该理想化折叠模型是由Wierzbicki和Abramowicz[6]给出的.这个单元含有水平固定铰(AB和BC)和倾斜移行铰(UB和BL)，其初始几何形状由该单元的总高度2H确定，a/2为AB和BC长度，h为方管壁厚.2ψ为2块相邻板间(平面ABU和平面CBU)的夹角，π-2β为UB和BL之间的夹角，γ为平面ABU中UB与顶边的夹角，当前单元几何状态描述可用下列参数描述：(上下)压溃距离为δ，侧板UBC的旋转角为α，或者C点的水平移动距离s.它们之间有如下关系：

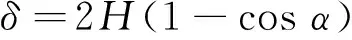
(1)

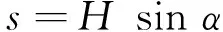
(2)

同时，γ(平面ABU中)和2β(平面UBL中)与ψ，α之间关系如下：

(3)

1.2原始材质方管塑性变形和能量耗散机理

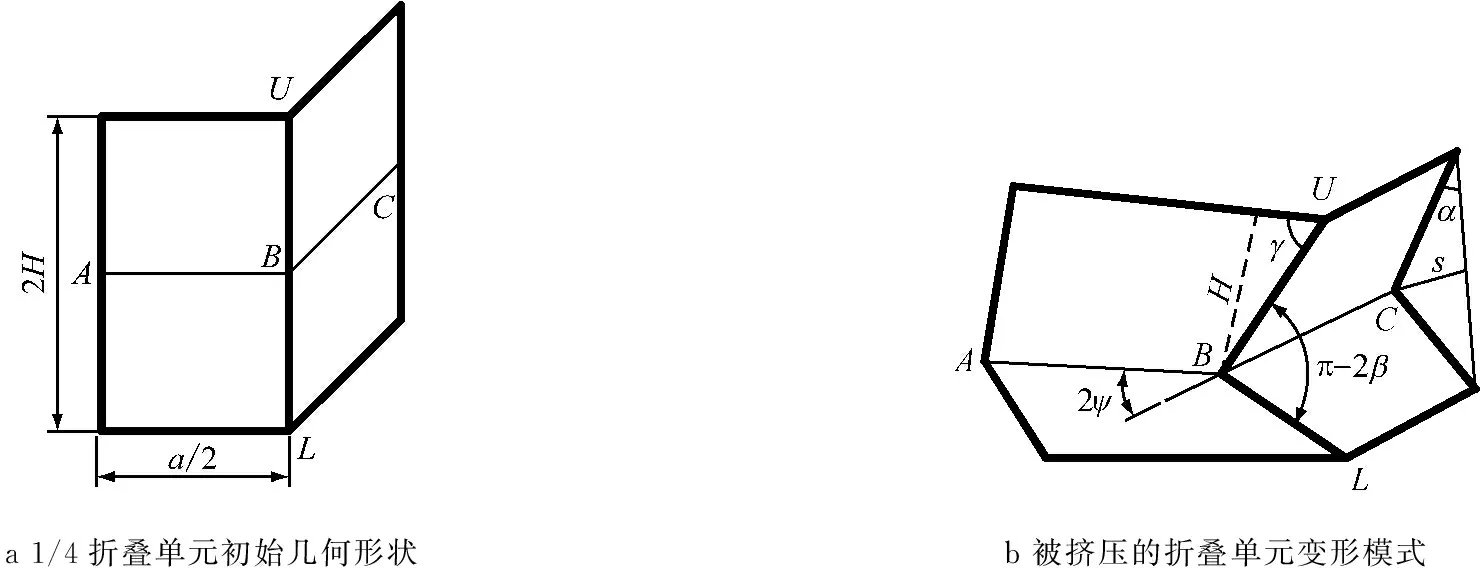
a1/4折叠单元初始几何形状b被挤压的折叠单元变形模式

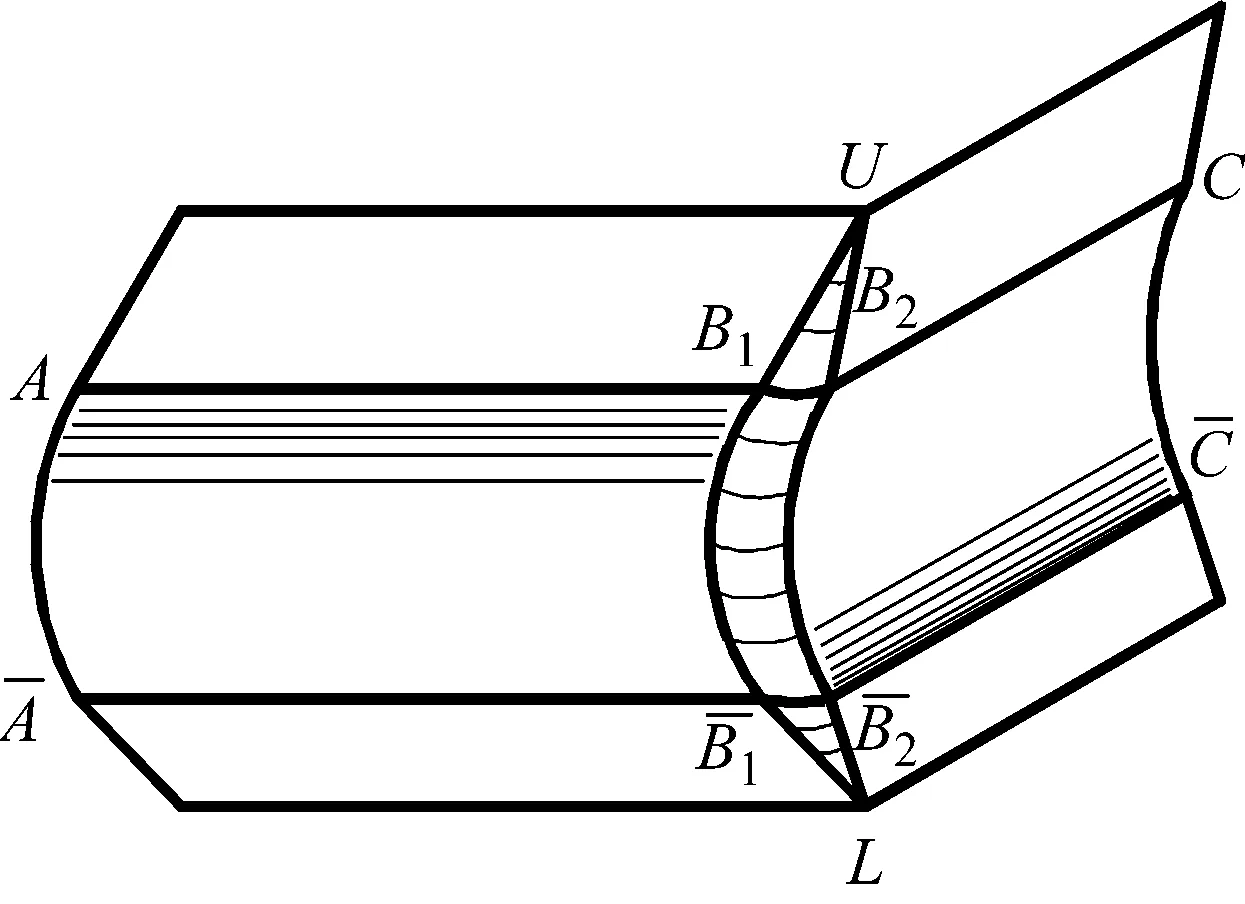
图2　实际运动许可的折叠机构

薄板通过环形曲面时，变形过程类似于材料被强制地从外部推向一个环形曲面，薄板有一个周向应变，环形区域内的塑性流动以周向应变形式为主，极限屈服膜力做内功，通过相应的几何积分可求得

(4)

式中：W1为薄板通过环形曲面的能量耗散；M0为单位长度的塑性极限弯矩，N，M0=Yh2/4，Y为材料屈服强度；b为圆环子午线方向半径，mm；I1(ψ) 为关于ψ的函数，具体表达式如下：

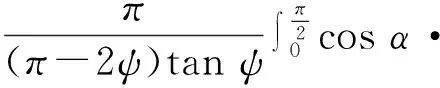
(5)

因为β可由式(3)转化α的函数，故可求出I1(ψ)，当ψ=π/4,I1(π/4)=0.58.

(6)

式中：W2为水平固定塑性铰的能量耗散；a为方形截面宽度，mm.

(7)

式中：W3为倾斜移行塑性铰的能量耗散；I3(ψ)是关于ψ的函数，具体表达式如下：

(8)

因为γ也可由式(3)转化为α的函数，故也可求出I3(ψ)，当ψ=π/4,I3(π/4)=1.11.

新媒体和地方传统媒体分别代表了不同视角的文化，两者之间存在的问题并不是不可调和的，与人们想象的恰恰相反，它们两者之间往往是相互促进，融合发展才能真正显示出它们的重要作用，发挥其最大的价值。虽然中国地方传统媒体展现出衰败的迹象，新媒体展现出一片光明的前途，但是社会在某些领域的话语权处于真空状态，为了填补这个真空需要地方传统媒体和新媒体的共同努力。

1.3棱线强化方管基本特征

棱线强化方管(ridgeline treatment square tube，RT)具有2种材料属性，即棱线与平板母材力学特性不同，母材为440级钢板，棱线部经过应力超高强度化处理.为避免发生Euler屈曲模式，需选取适当的宽厚比，其截面尺寸参数如图3所示，棱线部用粗线标出，平板部母材用细线标出，其中c=50 mm,s=5 mm,r=3.18 mm,h=1.0 mm.图4是方管三维实体模型，长度400 mm.

单向拉伸试验可获得母材屈服强度Y约为328 MPa，棱线部通过局部超高强度化处理，同理获得棱线部的屈服强度约为1 305 MPa，试验数据均摘自文献[9]，在此引入一个新的修正因子λ,λ为屈服强度比，λ=Yr/Yp，其中Yr为棱线部屈服强度，Yp为平板部屈服强度.

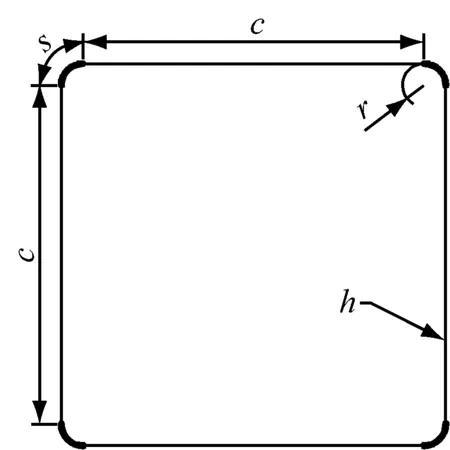
图3　棱线强化方管横截面尺寸

Fig.3Cross section parameters of ridgeline treatment square tube

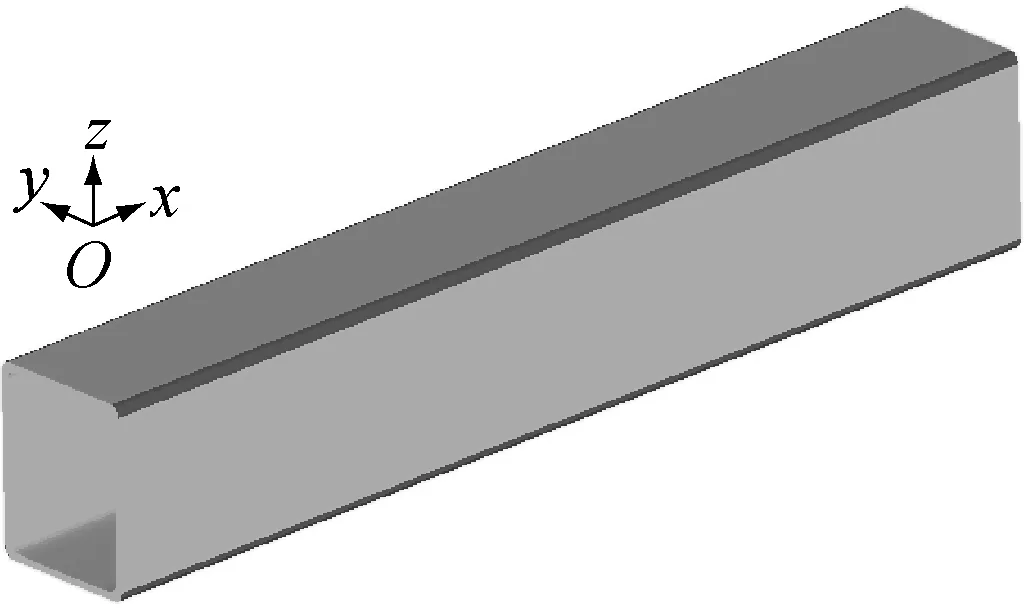
图4　棱线强化方管的三维实体模型

1.4棱线强化方管能量耗散假定和平均压溃力

显然，棱线强化方管具有2种材料属性，在变形模式上与单一材质方管的能量耗散机理不同.在此假定整个折叠单元的压溃塑性变形是完整的，且其变形模式不同点主要表现在如下3个方面：①通过环形曲面的能量耗散仍是通过环形塑性区的扩展实现，棱线局部增强会导致前述的垂直塑性铰即棱线部的塑性扩展难以进行，塑性扩展由棱线两侧的平板母材承担塑性区扩展，从而实现运动许可的塑性变形模式，所以能量耗散几乎不变，即W1不变；②水平固定塑性铰(AB和BC)通过平板和棱线的弯曲塑性变形来实现能量耗散，这个弯曲变形过程棱线会直接参与，故W2会略有上升；③对于倾斜移行塑性铰(UB和BL)，是棱线部的塑性弯曲和倾斜移动实现能量耗散，同时还带动棱线周边平板部的倾斜移动，故认为倾斜移行塑性铰的能量耗散W3将提高λ倍.

根据能量平衡要求，1/4模型的外力功Wert等于结构内部能量耗散，则有

(9)

考虑到典型吸能特性模型顶部和底部均出现有夹持状态下的水平固定塑性铰线，W2能量应该加倍.再分别将3个修正后的能量表达式代入，可得整个正方形折叠单元吸能模型的能量平衡式为

(10)

式中:Pm为平均压溃载荷，N.将平均载荷改写为如下一般形式:

(11)

式中：A1，A2，A3均为已知参数，上述方程中仅有2个未知数b,H，可通过分别令一阶偏导等于零，即

(12)

求解方程组可得

(13)

代入式(10)，有

(14)

本文取I1=0.58，I3=1.11，因此A1=32I1=18.56，A2=4π=12.56，A3=8λI3=8.89λ.从而，有

(15)

(16)

(17)

式(17)是棱线强化方管准静态轴向平均压溃力预测公式，形式与文献[6]中是相同的，可见λ和强化带分布主要影响的是等效吸能宽度，代入母材屈服强度Y=328 MPa，h=1.0 mm，c=50 mm，s=5 mm，λ=Yr/Yp≈4，可得该棱线强化方管的平均压溃力Pm≈20.519 kN.

2数值模拟

2.1仿真模型

利用Hypermesh9.0软件建立原始材质和棱线强化方管准静态轴向压溃有限元模型，然后导入LSDYNA 970进行数值计算.首先取边长1 m、厚度10 mm的方形薄钢板，其对边简支、另一对边固定，法向施加1 MPa面载荷进行线弹性有限元仿真分析，仿真结果表明：选用16号单元，壳体单元边长与厚度比介于1.5～12.5，且厚度方向积分点至少5个，方形薄板中部的最大挠度仿真值与解析解的偏差不超过1%；而当比值小于等于1或大于等于25时，偏差则大于6%，故不建议采用.所以方管主体划分为4节点的16号薄壳单元，壳体单元平均边长为2.0 mm，选用Mat24材料模型，刚性压板也划分为4节点薄壳单元，单元边长是5 mm，选用Mat20材料模型.2种材料的单向拉伸真实应力-塑性应变曲线均来自文献[9]，方管根部的截面压溃力等于刚性压板与方管之间的接触挤压力，仿真计算总时间设为0.32 s，轴向位移载荷320 mm施加在刚性板上，棱线强化方管的一端与刚性采用surface-surface接触算法，而另一端则施加固定约束.刚性压板运动方向仅限X轴向，各运动组件之间采用自动单面接触算法，摩擦系数均设为0.2，模型总单元数为22 625个，整个CAE仿真模型如图5所示.

图5　棱线强化方管数值仿真模型

2.2准静态模拟方法

LSDYNA显式积分计算的最小时间步长主要由最小单元特征长度和应力波在材料中的传播速率确定，CPU(central processing unit)求解总时间则由每一个循环时间步所需的CPU时间和时间步数来确定.显式积分算法因时间步长较小，比较适合做瞬态分析，而对于准静态压缩分析，过程时间较长，通常通过提高加载速率的方法来缩短计算时间，也可采用LSDYNA本身的质量缩放技术来加快计算进程.与质量缩放技术相比，提高加载速率可以更快获得仿真模拟结果，但须消除材料模型中应变率的影响[11].为了保证模拟计算的准确性，需考虑结构的惯性敏感性，王青春等[12]研究发现，利用提高加载速率的方法时，仿真计算的动能与内能之比应尽可能小，建议控制在2%以内.

2.3压溃塑性变形过程

图6a,6b是棱线强化方管准静态轴向压溃时的褶皱变形情况.仿真结果表明，棱线强化方管在准静态轴向压溃作用下发生了稳定的塑性屈曲变形，验证了本文选取的宽厚比能保证方管产生稳定塑性变形的预测.

图7完整复现了稳定阶段棱线强化方管一个新的折叠单元的形成过程，其塑性变形过程描述如下：当一个新的折叠单元开始准备产生时，棱线和平板几乎处于平直状态，随着刚性压板轴向压溃过程的恒速推进，在棱线部高强度支撑作用下，低强度的平板部率先开始出现弹塑性屈曲和面内拉伸以满足动力学许可的变形模式，由于上下平面外拱和两侧面内凹的双重塑性变形诱导，棱线部跟随平板部发生连续的水平弯曲移行，直至新折叠单元凹陷部的两侧棱线长度几乎相等的平衡状态，最后被轴向挤压对折形成一个新的折叠单元.上述数值仿真塑性变形过程验证了前述棱线强化方管的第①条不同变形模式假定，平板部仍以环形面的面内拉伸为主，故能量吸收几乎不变；同时在棱线强化方管在轴向压溃过程中，不难发现棱线部和平板部均参与了固定塑性铰线的弯曲，还表现出塑性铰和周边平板的移行变形来实现能量耗散，验证了第②和③条不同变形模式假定.

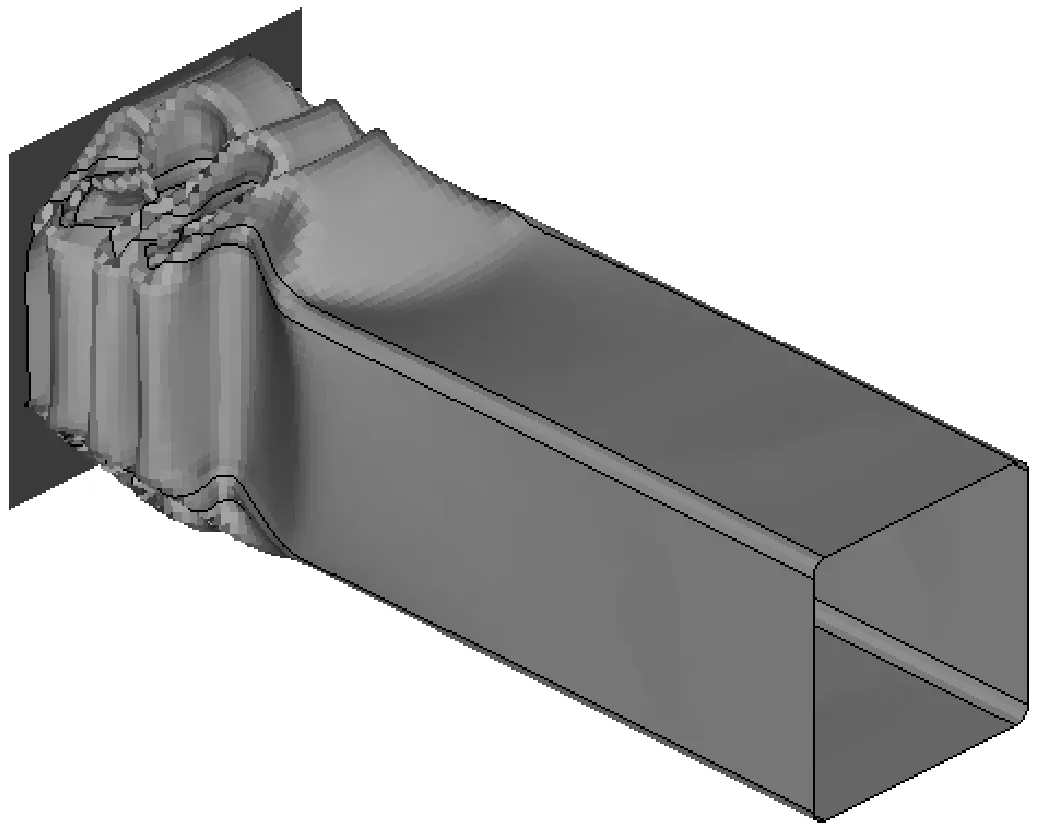
a t=0.2s

b t=0.3 s

2.4仿真结果讨论

棱线强化方管仿真计算压溃力变化如图8中实线所示，整个轴向压溃过程大致可分为3个阶段：

(1) 弹性屈曲阶段.方管4个平面先发生弹塑性变形，直至4条棱线开始弯曲，4个平板的折叠同时向外扩张，形成半个褶皱，压溃力达到最大值.

(2) 不稳定压溃阶段.方管完成第1个完全向外扩张的褶皱后，端部依然较平整，对第2个褶皱没有诱导效应，故第2个折叠单元的强化棱线直接挤压在第1个折叠单元上，导致第2个褶皱形成时压溃力波动幅度仍较大.

(3) 连续稳定的压溃阶段.从第3个褶皱开始，方管发生比较有规律的折叠变形，即图中约0.10 s之后棱线强化方管开始进入稳定压溃阶段，压溃力随之有规律地波动，波动幅度变小，这与文献[10]中典型方管的轴向压溃力实测曲线相符.

图8描绘了h=1.0 mm和h=1.4 mm的2种棱线强化方管压溃力变化曲线和平均压溃力.通常取稳定压溃阶段的平均值作为平均压溃力，如图8粗实线和细实线.经积分求和平均，h=1.0 mm和h=1.4 mm仿真平均压溃力分别为21.394 kN和36.062 kN, 对应的理论预测值分别为20.519 kN和35.949 kN，故两者中的最大偏差不超过4.3%，表明在准静态轴向压溃作用下棱线强化方管的平均压溃力预测公式(17)的准确性很高，可以满足工程设计需要.其次，图9对h=1.0 mm的原始材质和棱线强化方管压溃力进行了对比，显然棱线强化使方管压溃力有较大幅度的提升，其仿真压溃力平均值分别为21.394 kN和13.906 kN，增幅达到了53.8%，这是一个值得关注的仿真结果.

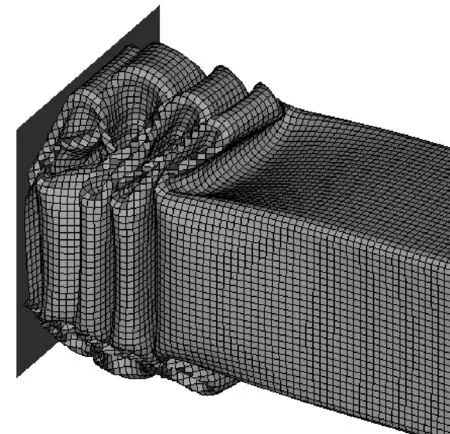
a t=0.222 s新折叠单元产生初始状态

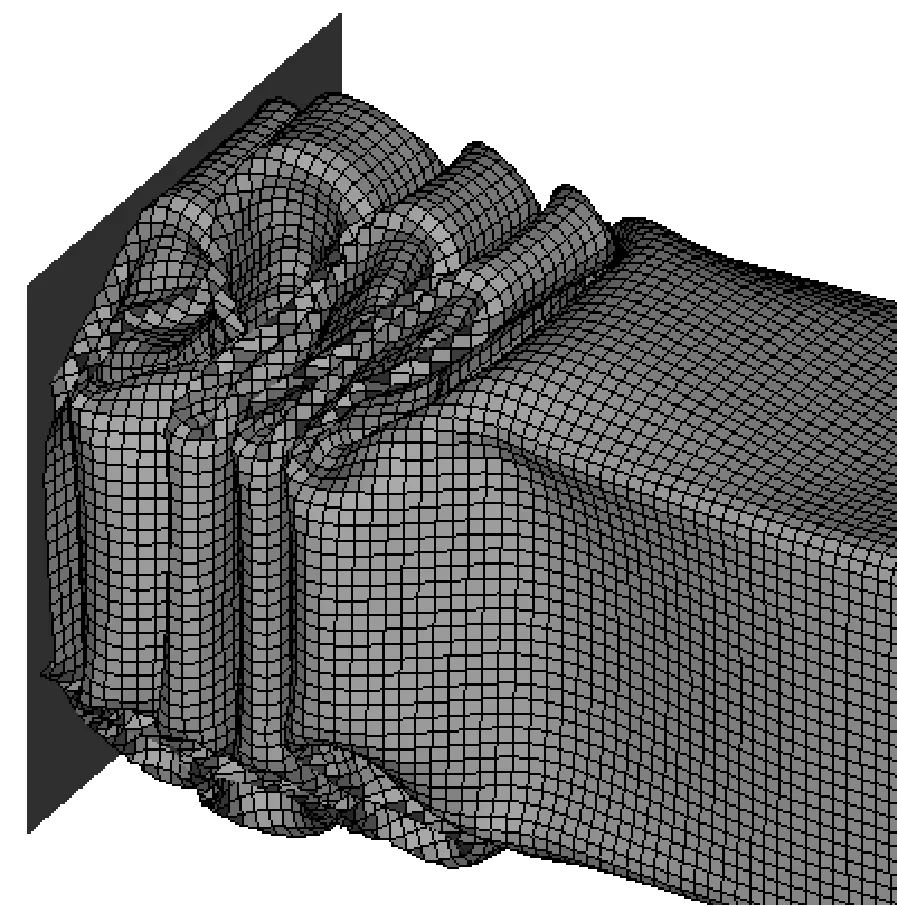
b 平板部屈曲发生

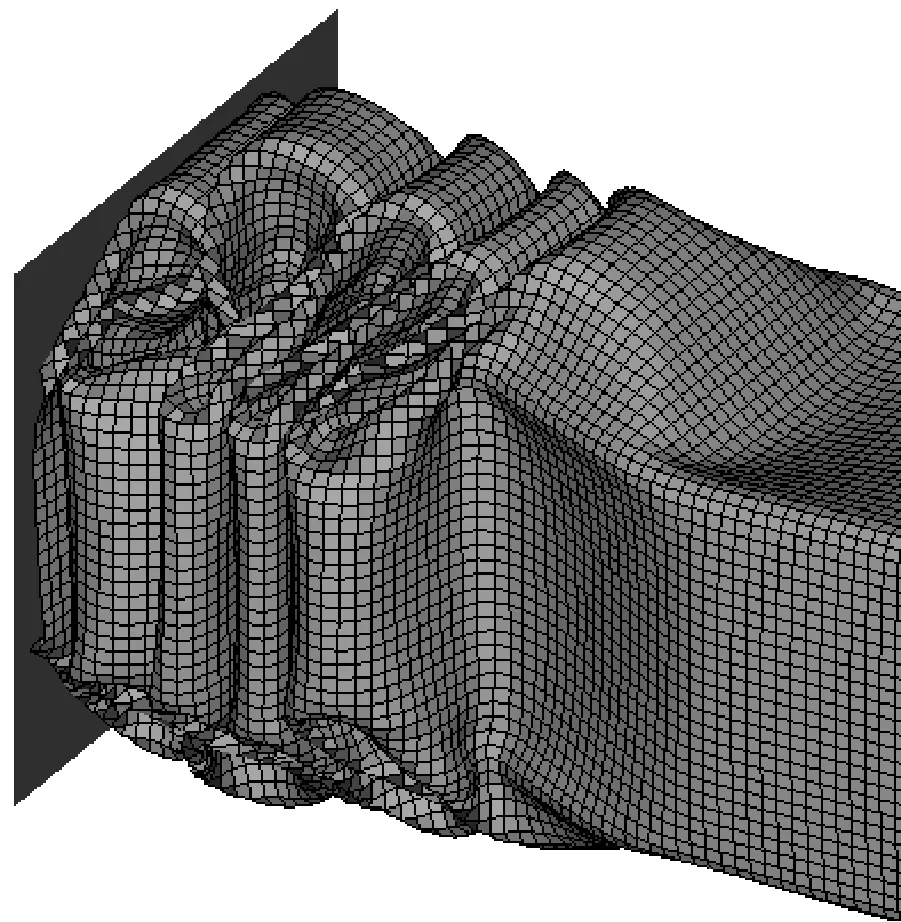
c 强化的棱线卷曲移行

d 新单元对称折叠

e t=0.254 s新折叠单元形成

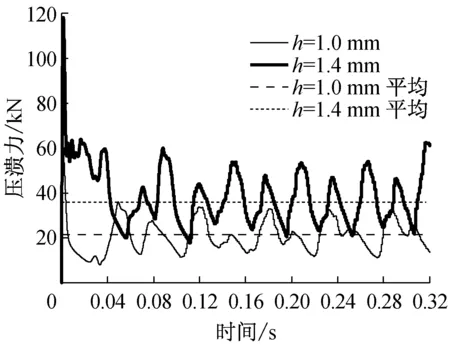
图8　棱线强化方管压溃力

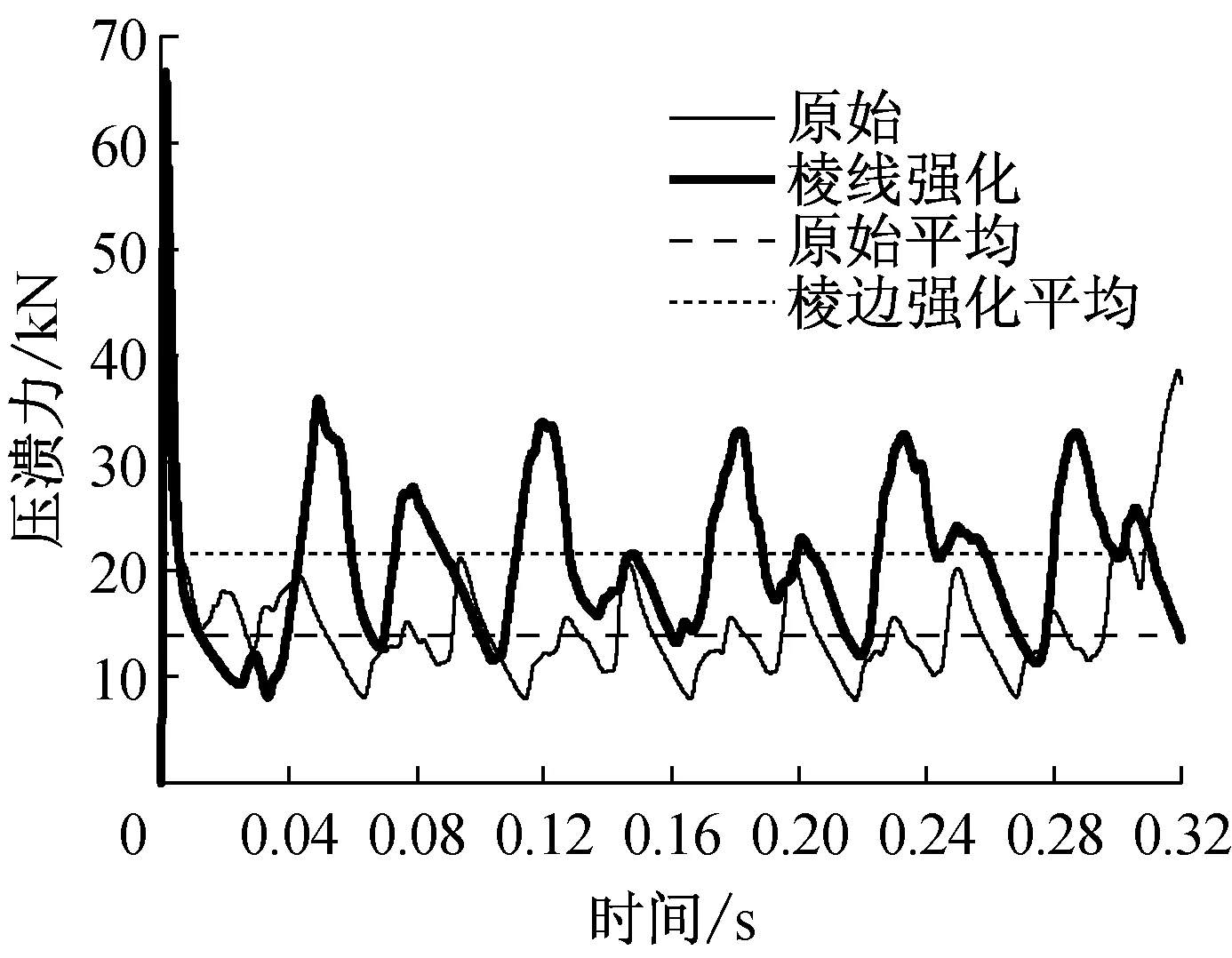
图9　h=1.0 mm时原始和棱线强化方管压溃力

3结论

基于Wierzbicki和Abramowicz 给出的方管理想化折叠模型和能量耗散分解法，结合能量平衡方程，引入棱线部和平板部的屈服强度比λ，修正获得了准静态轴向压溃作用下棱线强化方管的吸能方程和平均压溃力预测公式，理论和仿真分析了棱线局部强化对轴向压溃过程中方管的能量耗散模式的影响.

数值仿真完整再现了棱线强化方管在稳定压缩过程中一个新折叠单元的形成过程.壁厚1.0 mm和1.4 mm的棱线强化方管压溃力对比表明：仿真平均压溃力与理论预测值吻合得非常好，最大偏差为4.3%，可知棱线强化方管的平均压溃力预测公式(17)能够较准确预测其在准静态轴向压溃作用下的平均压溃力，该精确度可满足工程设计要求，但更大的宽厚比适用范围仍有待进一步验证.其次，由棱线强化和原始材质方管平均压溃力对比发现，仅强化占截面周长9.09%的4根棱线平均压溃力提升幅度可达53.8%，这个结果对于后期棱线强化技术在其他类似结构中的选择性设计开发和工程应用具有一定的参考价值.

参考文献:

[1]吴晓杰, 崔振山. 压弯联合作用下薄壁梁轴向压溃的条件[J]. 汽车工程，2014，36(8): 963.

WU Xiaojie, CUI Zhenshan. The conditions for axial collapse of thin-walled columns under the coaction of axial compression and bending moment[J]. Automobile Engineering, 2014, 36(8): 963.

[2]Aya N, Takahashi K. Energy absorption characteristics of vehicle body structures[C]//Transactions of the Society of Automotive Engineers of Japan. Tokyo: Society of Automotive Engineers of Japan, 1974: 65-74.

[3]Calladine C R. Theory of shell structure[M]. Cambridge: Cambridge University Press, 1983.

[4]Reid S R, Reddy T Y, Gray M D. Static and dynamic axial crushing of foam-filled sheet metal tubes[J]. International Journal of Mechanical Sciences, 1986, 28: 295.

[5]Meng Q, Al-Hassani S T S, Soden P D. Axial crushing of square tubes[J]. International Journal of Mechanical Sciences, 1983, 25 (9/10): 747.

[6]Wierzbicki T, Abramowicz W. On the crushing mechanics of thin-walled structures[J]. Journal of Applied Mechanics, 1983, 50: 727.

[7]Abramowicz W, Jones N. Dynamic progressive buckling of circular and square tubes[J]. International Journal of Impact Engineering, 1986, 4(4): 243.

[8]唐治, 潘一山, 李祈, 等. 矿用防冲方形折纹薄壁构件吸能特性数值分析[J]. 振动与冲击, 2014, 33(23): 87.

TANG Zhi, PAN Yishan, LI Qi,etal. Numerical analysis of energy-absorption properties of a thin-walled component with square folds for rock burst prevention in mine[J]. Journal of Vibration and Shock, 2014, 33(23): 87.

[9]Ji Ming, Abiko T, Okamura T. Compressive and bending collapse of box structure with different strength in ridgeline [C]//Transactions of Society of Automotive Engineers of Japan. Tokyo: Society of Automotive Engineers of Japan, 2015, 46(3): 645-652.

[10]余同希, 卢国兴. 材料与结构的能量吸收[M]. 华云龙, 译. 北京：化学工业出版社, 2006.

YU Tongxi, LU Guoxing. Energy absorption of structures and materials[M]. Translated by HUA Yunlong. Beijing: Chemical Industry Press, 2006.

[11]桂良进,范子杰,王青春. 泡沫填充圆管的动态轴向压溃吸能特性[J]. 清华大学学报:自然科学版, 2004, 44(5): 709.

GUI Liangjin, FAN Zijie, WANG Qingchun. Energy-absorption properties of foam-filled circular tubes subjected to dynamic axial crushing[J]. Journal of Tsinghua University: Science and Technology, 2004, 44(5): 709.

[12]王青春,范子杰. 利用Ls-Dyna计算结构准静态压溃的改进方法[J].力学与实践, 2003, 25(3): 20.

WANG Qingchun, FAN Zijie. Improvement in analysis of quasi-static collapse with Ls-Dyna[J]. Mechanics in Engineering, 2003, 25(3): 20.

收稿日期：2015-07-09

基金项目：国家“八六三”高技术研究发展计划(2012AA111302); 江西省交通厅重点工程项目(2015C0008)

通讯作者：朱西产(1962—)，男，教授，博士生导师，工学博士，主要研究方向为汽车安全技术. E-mail:xczhu@163.com

中图分类号：U465.11

文献标志码：A

Mechanical Properties of Thin-walled Square Tube with Strengthened Ridgelines Subjected to Axial Crushing

ZHENG Yuqing1, ZHU Xichan1, HU Qiang2, CHEN Zhibao2

(1. School of Automotive Studies, Tongji University, Shanghai 201804, China; 2. Institute of Applied Physics, Jiangxi Academy of Sciences, Nanchang 330029, China)

Abstract：Based on the energy dissipation modes and the ideal folding mechanism presented by Wierzbicki and Abramowicz, a modified energy balance equation was developed for the square tube with strengthened ridgelines subjected to quasi-static axial crushing by introducing a yield strength ratio between ridgeline and plate. Then a theoretical prediction formula of mean crushing force was also derived. CAE (Computer Aided Engineering) numerical simulation completely reproduced the plastic deformation process of a new folding element of square tube with strengthened ridgelines during stable crushing stage. Comparisons between simulation results and theoretical solutions show that the theoretical formula can correctly predict the mean crushing force for square tube with strengthened ridgelines subjected to quasi-static axial crushing, and the max deviation is lower than 4.3%. Secondly, for a specific square tube whose length, width and thickness of cross section is 56mm, 56mm and 1.0mm respectively, four strengthened ridgelines which only occupy 9.09% of perimeter of the cross section can increase its mean crushing force by 53.8%.

Key words：ridgeline strengthening; folding element; energy dissipation; numerical simulation; mean crushing force

第一作者： 郑玉卿(1983—)，男，讲师，博士生，主要研究方向为汽车碰撞吸能结构设计和CAE分析. E-mail:812york@tongji.edu.cn