地铁扣件螺旋道钉断裂过程分析及改进措施

肖　宏, 李启航

(1. 北京交通大学 土木建筑工程学院 道路与铁道工程系， 北京 100044；2. 北京市轨道交通线路工程安全与防灾工程技术研究中心， 北京 100044)



地铁扣件螺旋道钉断裂过程分析及改进措施

肖宏1,2, 李启航1,2

(1. 北京交通大学 土木建筑工程学院 道路与铁道工程系， 北京 100044；2. 北京市轨道交通线路工程安全与防灾工程技术研究中心， 北京 100044)

摘要：引入扩展有限元方法，结合现场调研与实测数据，建立均匀受力理想状态和偏载受力不利工况下螺旋道钉扩展有限元模型，通过预设横向、竖向微裂纹以及单条和多条微裂纹工况，分析研究了扣件螺旋道钉的裂纹发展过程.结果表明，由于螺旋道钉的道钉头部和螺杆结合部位存在较大的结构尺寸变化，导致了该处存在较大的应力集中，易萌生微裂纹，并在列车荷载长期作用下裂纹沿着横向扩展、贯通.对比看出，研究结果与实际扣件螺旋道钉的断裂形式相符，表明采用扩展有限元方法能很好地进行扣件螺旋道钉的断裂过程分析.此外，为避免和减少螺旋道钉的断裂发生，分13种工况研究了螺旋道钉肩胛过渡圆弧的设置.研究结果建议，对于T30×155型扣件螺旋道钉应设置1.6 mm半径的过渡圆弧，相对于不设置过渡圆弧，最大应力可减小40%.

关键词：螺旋道钉； 断裂过程； 扩展有限元法； 过渡圆弧

扣件作为轨道结构的重要部件之一，由弹条、轨下垫板、螺旋道钉等多个零部件组成，其中任一零部件出现失效或断裂都会直接影响扣件的正常工作以及线路的荷载分布、临近扣件的受力等，连续多个扣件断裂时还会直接影响列车运行的安全性.我国地铁大量采用了带螺旋道钉的扣件类型，调研发现在一些地铁线路存在普遍的螺旋道钉从肩胛部位断裂现象.

针对扣件的伤损、断裂问题，张志远[1]结合沪宁城际铁路使用的WJ-7B型弹性分开式扣件，调研、总结了扣件锚固螺栓松动的原因，并提出了相关的改善建议；王士强[2]对无砟有挡肩扣件松动、螺栓上浮的原因进行了分析，从安装和生产角度提出了改进措施；王峰等[3]针对螺旋道钉在受到意外锤击作用下发生松动或退出现象进行了调研和试验，提出将6mm垫圈换为4mm垫圈的解决措施；唐小萍等[4]对螺纹道钉抗拔力进行了试验，得出了以锚固剂的结合应力、螺纹道钉的锈蚀程度为自变量的螺纹道钉抗拔力表达式；徐立新等[5]针对起吊运输过程中道钉断裂现象进行分析，提出低温环境和强力组装是道钉断裂发生的原因；雷晓燕、李明华[6]通过建立力学分析模型对铁路桥梁护轨道钉断裂的原因进行了分析和研究，提出了减少道钉断裂的对策；Matthew等[7]使用试验和有限元相结合的方式进行了螺旋道钉的疲劳荷载分析；Ibrahim等[8]测试了用于复合材料轨枕的道钉抗拔力.此外，钟文文等[9]、肖志玲等[10]针对螺旋道钉的加工工艺进行了研究.

综上可以看出，现阶段针对扣件螺旋道钉断裂研究较少，且已有研究多以调研分析、物理实验以及传统有限元分析为主，针对T型螺旋道钉的损伤断裂过程研究未见报道.而明确扣件螺旋道钉的裂纹扩展、贯通直至断裂等演变过程对优化设计扣件产品、尽可能减缓扣件伤损病害、减少养护维修、确保列车运营安全具有重要的意义.近年来快速发展的扩展有限元方法在分析断裂、夹杂、不连续问题方面具有独特的优势，尤其在模拟裂纹扩展过程方面，是目前有限元难以做到的，如余江滔等[11]将扩展有限元用于剪力墙开裂的分析，杜修力等[12]采用扩展有限元法模拟了混凝土板的细观断裂破坏过程等.基于此，本文主要基于现场地铁扣件螺旋道钉的典型初始实际微裂纹情况，建立精细化的扩展有限元分析模型，分析扣件螺旋道钉断裂过程，揭示其断裂的主要原因及演变规律，提出改进措施，从而达到避免或有效减少扣件伤损断裂的目的.

1模型的建立

1.1螺旋道钉实体模型

地铁扣件采用的T型螺旋道钉型号为T30×155，材料为Q235-A，头部外径φ1=(50±1) mm，螺杆直径φ2=(31.0±0.5) mm，实物如图1a所示.现场调研发现，螺旋道钉的断裂绝大多数都出现在肩胛(螺帽和螺杆的结合部)位置，如图2a所示，从局部放大图2b断口可以看出，道钉头部与杆部结合处有明显的初期裂纹，有横向的也有竖向的，有的是单裂纹、有的是多裂纹.本文在理论分析时，为方便螺旋道钉的模型建立及网格划分，将螺帽的形状进行简化处理，建成圆形；同时，考虑到图1a螺旋道钉杆部的螺纹部分主要作用是将螺旋道钉固定在轨道板中，且现场未出现螺纹部分断裂的问题，为方便建模，在图1b有限元模型中将该螺纹段长度进行了全约束处理，以等效将杆部固定在轨道板中的力学作用.此外，考虑到螺旋道钉除了本身有预紧力外，还受列车动荷载作用下的往复上拔力作用.本计算模型采用将荷载施加在道钉头部下表面，以模拟上拔的作用效果，如图1b所示.

a道钉实物b有限元计算模型

a 整体图

b 局部放大图

螺旋道钉材料参数如表1所示.

表1　材料属性

1.2施加荷载的确定

1.2.1预紧力确定

扣件装配到地铁线路上后首先受到的基本作用力是预紧力F，其大小可通过螺栓受到的扭力矩T换算获得.根据经典理论，T与F有以下关系[13]：

(1)

式中：T1为螺纹副中的力矩；T2为支承面螺帽或螺母与角钢的接触面的力矩；d2为螺纹中径；α为牙型角；λ为螺纹升角；μ为螺纹间的摩擦系数；μ1为支承面间摩擦系数；dn为支承面的平均直径.

引入螺栓公称直径d对式(1)作一定变换可得

T=KFd

(2)

(3)

式中：K为工程中常用的扭矩系数，需要试验测量确定.

根据地铁线路设计，螺旋道钉的扭紧力矩应控制在200～250 N·m[14].表2为随机测试的北京地铁曲线地段螺旋道钉扭力矩值，从中可以看出，螺旋道钉普遍存在扭力矩不足和过扭的情况，扭力矩值较离散.

表2　扭力矩在不同统计区间所占比例

根据现场情况，本文的K值取0.202～0.253，由此可计算螺栓的预紧力，如表3所示.

表3　螺旋道钉预紧力计算结果

根据表3计算结果，本文螺旋道钉受力分析时道钉预紧力分别取10,20,30,40,50 kN.

1.2.2列车荷载确定

T型螺旋道钉工作时是紧密旋入道床板的预埋孔中的，在列车动荷载作用下难以直接通过测试获得道钉的空间受力.但可以通过在现场布置位移传感器测得列车作用下螺栓相对于轨道板的纵、横、垂向动位移，从而施加给计算模型.测试结果表明，螺旋道钉的位移主要是竖向变形，横向和纵向均非常小，可忽略不计.此外，从螺旋道钉的设计目的来看，也主要是承受垂向的振动荷载.因此，本文在模拟列车动荷载作用下道钉的受力时，计算模型采用了通过施加测试的垂向位移来模拟受力.螺旋道钉垂向位移现场测试结果为平均值0.51 mm、最大值1.44 mm、最小值0.41 mm、标准差0.12.本文计算中取最不利值1.44 mm.

1.3基于扩展有限元法螺旋道钉预设裂纹的实现

通过现场调查取样可以容易得到道钉的原始微裂纹情况(如图2).据此，可采用扩展有限元法建立有预设微裂纹的计算分析模型，图3为预设在道钉头部与螺杆结合部位的片状典型裂纹扩展有限元模型.

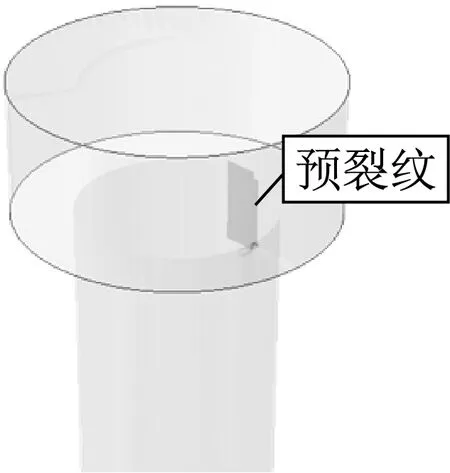
图3　T型螺旋道钉扩展有限元模型

根据扩展有限元基本原理，裂纹尖端的型函数可取为[15]

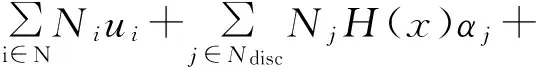
(4)

式中：i,j,k,α为节点符号；N为所有常规单元节点的集合；Ni,Nj,Nk为有限元形函数；x为一个点；ui为常规单元节点；Ndisc为完全被裂纹贯穿单元节点的集合；H(x)为跳跃函数，反映裂纹面位移的不连续性；αj为贯穿单元节点；Nasy为含裂尖单元的集合；bk为裂尖单元节点的位移；φα(x)为裂尖渐近位移场附加函数，可按下式计算：

(5)

式中：r,θ分别为原点定义在裂纹尖端局部极坐标系中的坐标，θ为裂纹尖端点的方向，r为裂纹尖端点距极坐标原点的距离.

由于螺旋道钉出现裂纹后发生断裂更接近脆性断裂趋势，因此伤损准则选取最大拉应力准则，伤损演化为基于能量的、线性软化的混合模式的指数伤损，如式(6)所示：

(6)

式中：GI为普通模式下的断裂能;GⅡ,GⅢ为剪切模式下的断裂能；GIC为普通模式下的断裂能临界值；GⅡC,GⅢC为剪切模式下的断裂能临界值；β为指数.

参考相关测试值[16]，本文GIC=GⅡC=GⅢC=80.033 N·mm，β=1.

2道钉断裂过程模拟分析

设计的螺旋道钉应在均匀荷载作用下工作.但现场调研发现，在安装过程中螺旋道钉受下部垫片以及加工精度的影响常出现头部部分受力、部分悬空的现象(偏载作用).因此，分别研究均匀荷载(理想状态)作用与偏载作用(实际常见状态)下道钉的断裂过程.

2.1均匀荷载作用

根据现场调研，T型螺旋道钉出现的裂纹形式多种多样，其中横向或竖向原始裂纹是最常见的典型形式.因此，探讨均匀荷载作用下这2种工况下的道钉断裂过程，其他方向的裂纹断裂规律类似，这里不再赘述.根据表3计算结果，取最不利工况，下述分析时均匀荷载情况是在道钉头部下表面均匀施加50 kN预紧力和1.44 mm垂向位移.

在具体分析道钉的断裂过程时，限于篇幅，仅选取裂纹发展初期(裂纹开始发展)、中期(裂纹发展过程中)、末期(裂纹发展贯通)3个阶段的三维立体透视图，对比分析其断裂发展规律.

2.1.1横向微裂纹

计算的横向微裂纹发展过程如图4所示.由图4a可以看出，在荷载作用下，首先道钉头与螺杆结合处出现应力集中，然后进一步发展为横向裂纹.由图4b,4c,4d可以看出，随着荷载继续作用，横向裂纹沿着结合截面横向发展，并最终趋于横向贯通.这与现场T型螺旋道钉的断裂情形相吻合，即断裂位置的头部与杆部结合处基本成平面断口，如图1所示.

2.1.2竖向微裂纹

图5的计算条件同图4，所不同是在模型中将横向微裂纹改成了竖向微裂纹.模型计算的竖向微裂纹发展过程如图5所示.从图5的竖向微裂纹发展过程来看，尽管最初的微裂纹呈竖直方向，但随着荷载继续作用，裂纹将出现和图4一致的结果，即初始的竖向裂纹发展为横向并逐渐贯通.

a应力集中现象b初期

c中期d末期

a初期b中期c末期

综上，从以上横向、竖向2种形式的裂纹发展过程分析可知，在均匀荷载作用条件下，道钉头部与杆部结合处横向、竖向的原始裂纹最终都会沿着结合部横向发展，并最终贯通、断裂.这主要是由于在道钉头部与螺杆结合部结构尺寸变化剧烈，易产生应力集中，从而萌生裂纹并断裂，也由此揭示了道钉普遍的断裂型式为沿结合部的平面断口，即图1所示情况.这也间接验证，采用扩展有限元进行扣件螺旋道钉断裂过程分析方法可行，分析结果与实际情形相符.

2.2偏载作用

根据表3，取最不利工况，偏载仅施加在道钉头部1/2下表面，大小为50 kN预紧力和1.44 mm垂向位移.

(1) 单条竖向裂纹.与均匀荷载计算工况类似，偏载作用下在道钉头部与杆部结合处预设一竖向裂纹，计算分析其发展变化过程，如图6所示.从图可以看出，偏载作用下裂纹的发展变化与均匀荷载作用下规律类似，竖向裂纹最后发展为横向裂纹，并扩展贯通.

a初期b中期c末期

(2) 多条竖向裂纹.本工况在道钉头部与杆部结合处预设2个相同大小的初始微裂纹，计算的裂纹发展过程如图7所示.从图7的裂纹扩展过程来看，竖向裂纹的扩展最终都转向为沿道钉肩胛的横向裂纹，并趋于扩展贯通，与前述单条裂纹扩展规律类似.

a初期b中期c末期

(3) 道钉头部表层竖向微裂纹.由于材质缺陷、施工荷载等因素，部分扣件的螺旋道钉头部也存在微裂纹.计算头部微裂纹扩展过程如图8所示.图8a为表层的初始裂纹向下逐渐发展，图8b为裂纹已经发展到头部与螺杆结合位置且螺杆平面部位产生小面积开裂区域，图8c为裂纹贯穿部分道钉头部.由

a初期b中期c末期

此发展历程可以看出，道钉头部出现裂纹后，偏载作用下裂纹会向道钉肩胛处发展并最终横向扩展、贯通.

由上述3种计算工况可以看出，对于扣件螺旋道钉，无论最初的微裂纹是在螺杆上还是在道钉头部，最终都会发展到道钉肩胛处，并沿横向扩展.由此进一步揭示了地铁现场看到的螺旋道钉断裂大多是头部和杆部结合处的平面断口型式，如图1所示.

3过渡圆弧对道钉断裂的影响

从上述计算结果可知，螺旋道钉在受力后容易在道钉头部与螺杆结合处产生应力集中，从而萌生裂纹并最终发展、断裂.这主要是由于在道钉头部与螺杆结合处存在剧烈的结构尺寸变化所致.因此，为改善螺旋道钉受力、减轻应力集中、尽可能避免道钉折断，应该在道钉头部与杆部的结合处加工成合适的过渡圆弧.

现场调研发现，由于所使用的道钉生产厂家不同、加工精度各异，在结合部位未设置过渡圆弧或存在过渡圆弧加工不当的情况较普遍.基于此建立不同过渡圆弧的道钉模型，对比分析道钉过渡圆弧处应力大小，优化扣件螺旋道钉设计.不同的道钉模型为：道钉过渡圆弧半径R分别取0,0.1,0.2,0.3,0.4,0.5,0.6,0.8,1.0,1.2,1.6,2.0,2.5 mm 13种工况，每种工况分析在10,20,30,40,50 kN预紧力作用下的受力.

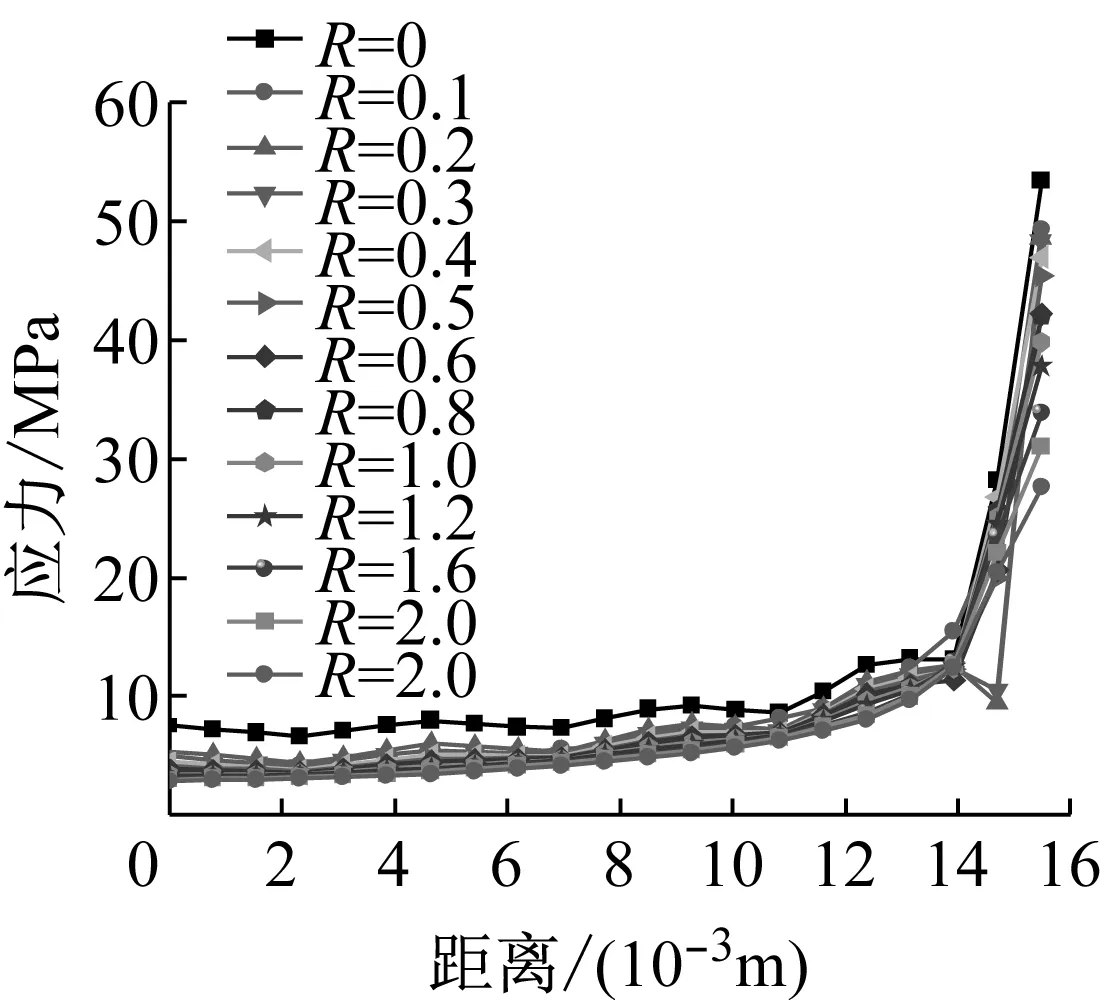
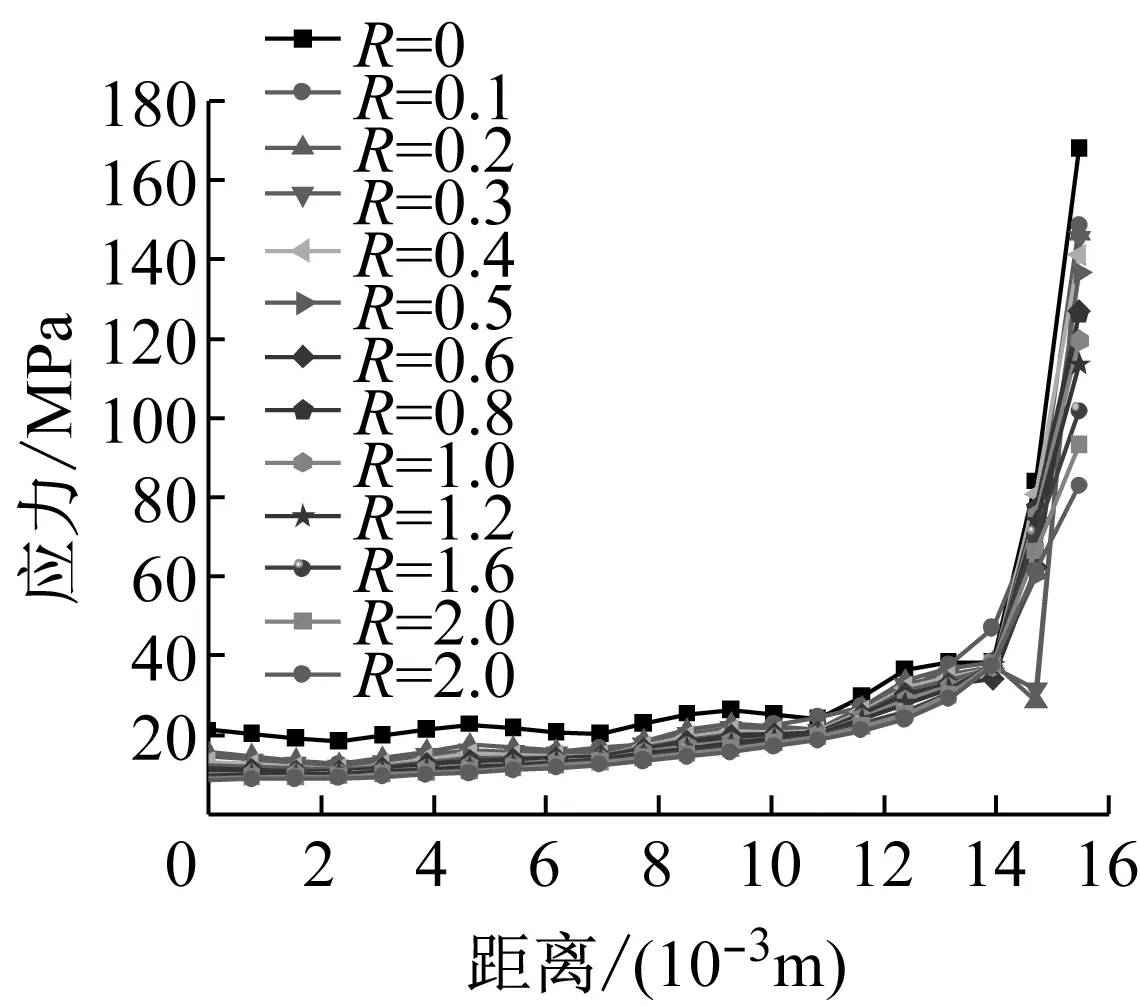
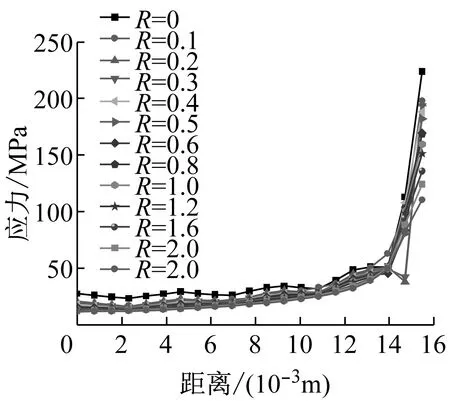
为方便分析，提取从道钉中心到过渡圆弧应力集中处不同位置的应力如图9所示，计算不同工况应力变化如图10所示，该计算分析结果为螺旋道钉合理设计优化提供依据.

对比分析以上13种工况下图10所示螺旋道钉肩胛处从中心到表面的应力变化，可以发现：

(1) 各工况下道钉受力的变化规律基本一致，

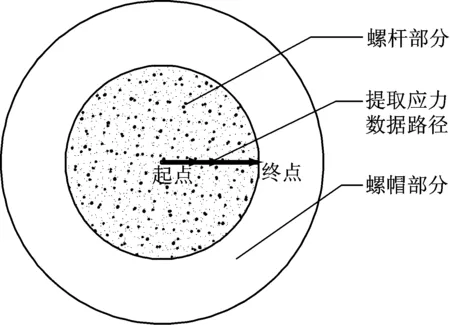
图9　提取应力数据路径

a F=10 kN

b F=20 kN

c F=30 kN

d F=40 kN

e F=50 kN

均由中心向外表面逐渐增大.其中，肩胛处的应力明显大，属于高应力区，易萌生裂纹；这也说明了扣件道钉断口为什么在靠近外侧处先出现微裂纹，然后在长期列车荷载作用下才发生断裂.

(2) 相对于有过渡圆弧的工况，无过渡圆弧工况肩胛处应力明显增大.以40 kN上拔力作用工况为例，无过渡圆弧工况最大应力值为225.3 MPa，当过渡圆弧R=1.6 mm时最大应力值为135.6 MPa，减小了39.8%.

(3) 随着过渡圆弧半径增加，在相同上拔力作用下，肩胛处应力整体上减少.以40 kN上拔力作用工况为例，当过渡圆弧从R=0.1 mm变化到R=2.5 mm时，最大应力由197.5 MPa减小到110.5 MPa，减小了44.1%.可见，设置过渡圆弧对改善螺旋道钉应力集中非常有效.

提取不同过渡圆弧情况下的螺旋道钉肩胛最大应力变化规律如图11所示.从图可以看出，在不同预紧力作用下，螺杆最大应力均随着过渡圆弧半径的增大而基本呈线性减小.此外，还可从图看出，在相同的过渡圆弧半径下，施加的荷载越大、道钉肩胛处受到的应力越大.由此表明，改善扣件受力与设置螺旋道钉过渡圆弧半径是减小螺旋道钉受力、折断的有效措施.其中，对于改善扣件受力，需要从设计、运营等多方位考虑.而对于设置过渡圆弧，考虑到道钉设计直径为φ=(31.0±0.5)mm，结合文献 [17]，当φ在30～50 mm时，R取1.6 mm.因此，建议地铁扣件螺旋道钉的过渡圆弧加工成1.6 mm半径的圆弧，以减小应力集中.从图11可知，设置1.6 mm半径的圆弧较无过渡圆弧的工况，最大应力可减小40%，能大大减缓其折断的趋势.

图11　螺旋道钉肩胛处最大应力变化图

4结论

(1) 引入扩展有限元方法进行地铁扣件断裂过程分析，结果表明，扩展有限元方法在计算分析螺旋

道钉断裂方面具有独特的优势，尤其对裂纹的发展过程能够进行清晰直观的模拟，模拟结果与实际情况相符.

(2) 对道钉的断裂过程分析表明，无论扣件螺旋道钉的初始微裂纹是横向还是竖向，裂纹是单条或者多条，均会发展为沿结合部位的横向扩展，并最终断裂，很好解释了地铁螺旋道钉的断裂大多表现为沿道钉头部与杆部结合处的平面断口形式.

(3) 在道钉头部与杆部结合处设置过渡圆弧可以有效减小道钉肩胛处的应力集中问题，从而有效减缓或避免扣件的断裂问题.计算分析建议，T30×155螺旋道钉宜采用R=1.6 mm的过渡圆弧，相对于不采用过渡段圆弧情况，应力可以减小40%.

参考文献:

[1]张志远. WJ-7B型扣件锚固螺栓松动原因及防松对策[J]. 上海铁道科技,2014(1):50.

ZHANG Zhiyuan.WJ-7B type fastener anchoring bolt looseness reason and locking countermeasures[J]. Shanghai Railway Science,2014(1):50.

[2]王士强. 浅谈铁路轨道板扣件存在问题[J]. 科技创新与应用,2013(7):168.

WANG Shiqiang. A brief introduction of railway track slab fastener problems[J].Science And Technology Innovation And Application,2013(7):168.

[3]王峰,肖俊恒,方杭玮，等. 沪杭客专扣件螺旋道钉锤击松退原因分析及处理措施研究[J]. 铁道建筑,2011(12):99.

WANG feng, XIAO Junheng, FANG Hangwei,etal. Analysis on the hammer blow unclenching causes and treatment measures of Shanghai—Hangzhou passenger dedicated fastener screw spike [J]. Railway Engineering,2011(12):99.

[4]唐小萍,郭保生,刘庆潭. 螺纹道钉锚固抗拔力的分析和研究[J]. 铁道学报,2009,31(5):130.

TANG Xiaoping,GUO Baosheng, LIU Qingtan. Analysis on anchor withdraw resistance of screw spike[J]. Journal of the China Railway Society,2009,31(5):130.

[5]徐立新,王顺花. 双头螺旋道钉断裂分析[J]. 理化检验：物理分册,2005,41(3):137.

XU Lixin, WANG Shunhua. Fracture analysis of double-head-twisted spikes[J]. Physical Testing and Chemical Analysis Part A: Physical Testing, 2005,41(3):137.

[6]雷晓燕,李明华. 铁路桥梁护轮轨螺旋道钉断裂分析[J]. 铁道工程学报,1999(2):31.

LEI Xiaoyan,LI Minghua. Nalyses of clip bolt fracture for guard rail of rail-way bridge[J]. Journal of Railway Engineering Society,1999(2):31.

[7]Dick Matthew G, McConnell David S, Iwand Hans C. Experimental measurement and finite element analysis of screw

spike fatigue loads[C]∥Proceedings of the ASME/IEEE Joint Rail Conference and the ASME Internal Combustion Engine Division, Spring Technical Conference 2007. New York :American Society of Mechanical Engineers, 2007: 161-166.

[8]Ibrahim Lotfy, Maen Farhat , Mohsen A Issa. Structural behavior of rail fastening system used for recycled plastic composite crossties[C]. ASME/ASCE/IEEE 2015 Joint Rail Conference. New York:American Society of Mechanical Engineers, 2015: 1-8.

[9]钟文文,万今仪. 广州地铁轨道单趾弹簧扣件锚固螺栓的研制[J]. 铁道建筑,2001(1):10.

ZHONG Wenwen, WAN Jinyi. Development of anchor bolts of Guangzhou metro rail single toe spring fastener[J]. Railway engineering,2001(1):10.

[10]肖志玲,刘百宣,刘华,等. 螺旋道钉多工位冷镦成形工艺优化及数值模拟[J]. 锻压技术,2014(2):79.

XIAO Zhilin，LIU Baixuan，LIU Hua,etal. Process optimization and numerical simulation of multistage cold heading for railway screw spike[J]. Forging&Stamping Technology,2014(2):79.

[11]余江滔,陈竟,陆洲导，等. 超高韧度水泥基修复剪力墙试验的数值分析[J]. 同济大学学报：自然科学 版，2015,43(2):175.

YU Jiangtao,CHEN Jing,LU Zhoudao,etal. Numerical analysis on damaged reinforced concrete shear wall repaired with engineered cementitious composites[J]. Journal of Tongji University：Natural Science,2015,43(2):175.

[12]杜修力,金浏,黄景琦. 基于扩展有限元法的混凝土细观断裂破坏过程模拟[J]. 计算力学学报,2012,29(6):940.

DU Xiuli,JIN Liu,HUANG Jingqi. Simulation of meso-fracture process of concrete using the extended finite element method[J]. Chinese Journal of Computational Mechanics,2012,29(6):940.

[13]许镇宇,朱景梓, 郑林庆，等．机械零件[M]．北京:人民教育出版社,1960.

XU Zhenyu, ZHU Jingzi, ZHEN linqin,etal. Mechanical elements[M].Beijing: People’s Education Press, 1960.

[14]吴建忠,李湘久,武江虹. 北京城市铁路弹性扣件的研究设计[J]. 铁道建筑,2003(S1):11.

WU Jianzhong, LI Xiangjiu,WU Jianghong. Design of Beijing urban railway elastic fasteners[J]. Railway Engineering,2003(S1):11.

[15]Belytschko T, Gracie Robert. On XFEM applications to dislocations and interfaces[J].International Journal of Plasticity, 2007, 23(10):1721.

[16]赵章焰,孙国正. 用柔度标定法测量Q235钢断裂韧性[J]. 武汉理工大学学报:交通科学与工程版,2002(4):441.

ZHAO Zhangyan,SUN Guozheng. Measuring fracture toughness of Q235 steel using flexible method[J]. Journal of Wuhan University of Technology:Transportation Science & Engineering, 2002(4):441.

[17]陈宏均.实用机械加工工艺手册[M].北京：机械工业出版社，2009.

CHEN Hongjun. Practical machining process manual[M].Beijing: China Machine Press，2009.

收稿日期：2015-07-24

基金项目：中央高校基本科研业务费专项资金(2014JBZ012)

通讯作者：李启航 (1990—)，男，硕士生，主要研究方向为道路与铁道工程. E-mail:10232039@bjtu.edu.cn

中图分类号：U213．244

文献标志码：A

Fracture Process Analysis and Improvement Approach of Subway Fastener Screw Spike

XIAO Hong1,2, LI Qihang1,2

(1. Highway and Railway Engineering， School of Civil Engineering Department， Beijing Jiaotong University, Beijing 100044， China；2. Beijing Engineering Research Center of Rail Traffic Line Safety and Disaster Prevention, Beijing 100044，China)

Abstract：Based on field investigation and experimental data, extended finite element method was introduced to establish uniform stress model and non uniform stress model under adverse conditions. Horizontal, vertical micro cracks, single and multiple cracks were set up to study the crack development process of the fastener screw spike. The result shows that due to abrupt size change in the screw spike combining site of the head and screw, there is large stress concentration, easily generates micro cracks and then lateral extends, eventually breakdown under long-term train load. Simulation resultswere in conformity with actual fastener screw spike fracture form, so the extended finite element method is very suitable for fastener spike fracture process analysis. In addition, in order to avoid and reduce the screw spike rupture occurring, 13 kinds of working condition were studied about fastener screw spike shoulder transition arc setting. The result shows that the ideal arc radius is 1.6 mm for T30×155 type fastener screw spike, and the maximum stress will be reduced by 40% relative to without transition arc.

Key words：screw spike; fracture process; extended finite element method; transition circular arc

第一作者： 肖宏(1978—)，男,副教授，工学博士，主要研究方向为道路与铁道工程. E-mail:xiaoh@bjtu.edu.cn