既有铁路开行大轴重列车路基的动力稳定性

肖军华，郭鹏飞，周顺华，狄宏规

(同济大学 道路与交通工程教育部重点实验室， 上海 201804)



既有铁路开行大轴重列车路基的动力稳定性

肖军华，郭鹏飞，周顺华，狄宏规

(同济大学 道路与交通工程教育部重点实验室， 上海 201804)

摘要：为研究既有铁路开行大轴重列车路基的变形和强度稳定性，选取既有线典型路基土，借助动三轴仪，试验研究了重载下路基土的累积塑性应变和临界动应力，建立了路基土累积应变的预估公式；在此基础上，通过动力有限元分析得到了重载下路基的动应力，并基于分层总和法的思想计算了路基的动力附加变形. 研究表明，当路基压实系数低、饱和度高时，路基动力附加变形随列车轴重增加迅速增大，且轴重超过27 t，增大速率明显加快，但当路基压实系数大于一定条件，轴重增加对路基附加变形的影响较小；重载下路基动力附加变形的影响深度主要在2.5 m内，且显著影响深度约为1.0 m；重载下路基未发生动强度破坏情况下也会产生不能接受的永久变形. 可通过提高路基压实系数(或强度)显著减少重载下路基的附加变形量和变形达到稳定的时间.

关键词：既有线路基； 重载； 临界动应力； 动力附加变形

提高轴重是提高铁路重载运输能力和效益的重要途径. 我国铁路通用线路轴重23t，专用线路轴重25t，与重载运输先进国家有较大差距. 根据2013年颁布的《铁路主要技术政策》:“今后专用线要按30t轴重标准设计，既有线要开行27t轴重的货车”,可知大轴重、长编组是我国今后铁路重载运输的发展方向.

在重载条件下，路基动荷载增大、荷载作用深度加深、路基受到的连续荷载作用次数也增加，对路基沉降产生影响[1]. 特别是对既有铁路而言，在填料等级和压实系数偏低、路基已存在病害的情况下，增开大轴重列车势必影响路基的长期动力稳定性. 如南非某运煤专线的路基设计荷载未按重载标准考虑，开通后路基未进行加固，随着运行时间增加，路基出现裂缝、边坡塌落等病害，危及列车正常运行[2].

目前，国内外在重载铁路路基工程、铁路路基动力稳定性等方面开展了大量研究. 针对前者，美国、澳大利亚、南非等发展重载铁路的国家在路基基床结构、路基填筑质量以及路基防排水和边坡防护等方面制定了较高的技术标准[3-5]；近年来，我国也开展了路基加固强化的相关试验和检测技术，分析了重载铁路路基荷载特征和路基动力响应，对既有铁路重载扩能的路基强度条件进行了评估等[6-8]. 针对后者，国内外学者通过动三轴试验对列车荷载作用下路基土的累积变形、临界动应力等进行了研究，探讨了列车荷载幅值、加载频率以及路基土的物理状态等影响规律，并建立了土体累积变形模型预测路基长期沉降[3-4,9].

然而，现有研究并未结合重载下路基的动荷载特征、既有铁路路基的实际物理力学状态以及动荷载作用下路基土的变形、强度特性对既有铁路开行大轴重列车路基的长期动力稳定性进行分析评估. 本文结合几条既有铁路路基的物理力学参数的调查数据，通过分析重载下路基动荷载特征、列车荷载作用下路基土累积变形和临界动应力，探讨了既有铁路开行大轴重列车路基的强度和变形动力稳定性，具有一定的实际意义.

1列车荷载作用下路基土的变形和强度特性

1.1既有铁路路基的物理力学状态

表1统计了大秦、朔黄2条既有重载铁路部分区段路基基床的土工参数，包括天然含水率w和压实系数K等，路基土质均为粉土或黏质粉土，属C组填料. 同时，表1也列出了与2条重载铁路的路基土性质接近的其他几条普通既有铁路路基基床的土工参数. 表中wL为液限含水率、wp为塑限含水率、Ip为塑性指数、wopt为最优含水率、γmax为最大干密度、γ为实测干密度. 从表1可以看出，既有线路基的天然含水率明显高于其最优含水率，两者的比值最大为2.23，平均约为1.5；路基土的现场干密度低于其最大干密度，路基的压实系数最大值为0.92，均值为0.83. 可见，既有线路基基床土质总体欠佳.

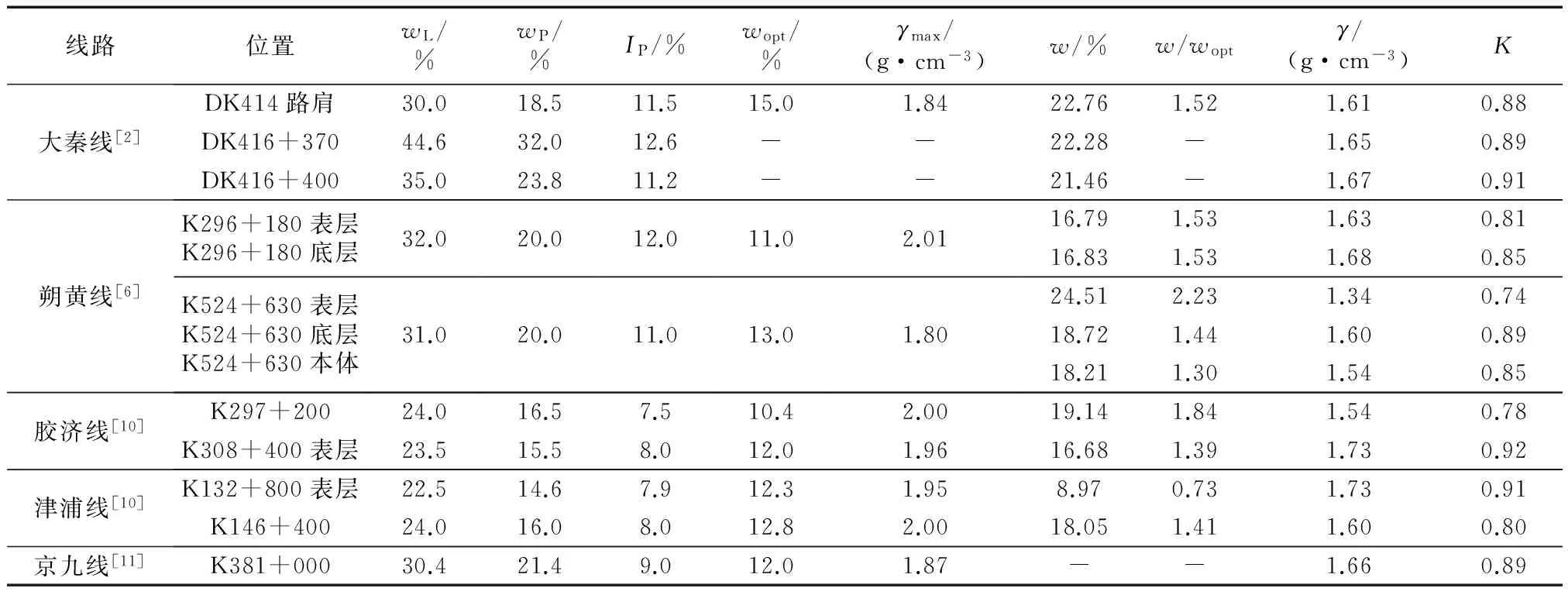
表1　既有铁路路基基床的土工参数

1.2列车循环荷载下路基土的动力特性

1.2.1试验条件

研究表明[12]，路基土的动力特性主要受动应力水平、加载频率、路基土的物理状态和土性等因素的影响. 为研究重载条件下路基土的动力特性，需从路基的动荷载特征和路基土的物理状态两方面尽可能模拟现场的实际条件.

已有测试表明[1]，路基动应力幅值与列车轴重基本上成正比，将动应力以单位轴重进行归一化处理，动应力σd(kPa)的平均值与列车轴重P(t)的关系在数值上约为σd,avg=2P. 考虑到轨道结构状况等的变化，动应力幅值的最大值在数值上约为σd, max=4P，若考虑最大列车轴重30t，则应主要研究动荷载幅值不超过120 kPa时路基土的动力特性. 路基土的加载频率f与列车运行速度v、车长l、转向架距离、轴距等有关，但对路基影响最大的频率是车辆的通过频率f，即f=v/l，因此主要考虑低频作用(1～2 Hz)对路基土动力特性的影响. 试验表明[12]，在路基动荷载幅值范围内，该频率范围对路基土动力特性的影响有限. 此外，由于路基土的天然含水率一般高于其最优含水率，因此，主要考察路基土含水率在最优含水率湿侧的情况. 拟定的试验条件如表2所示. 表中σ3为围压，N为列车荷载循环次数，K为压实系数，ω为实测含水率.以黄河冲积粉土(表1京九线K381+000工点)为例[11]，开展列车荷载下路基土动力特性的试验. 表3列出了不同K和各次w条件下试样的强度，其中静极限强度取单调加载下试样应力-应变曲线的峰值点，临界动应力取循环加载下试样界于稳定和破坏的应力水平[12]，表中Sr为饱和度.

表2　动三轴试验条件

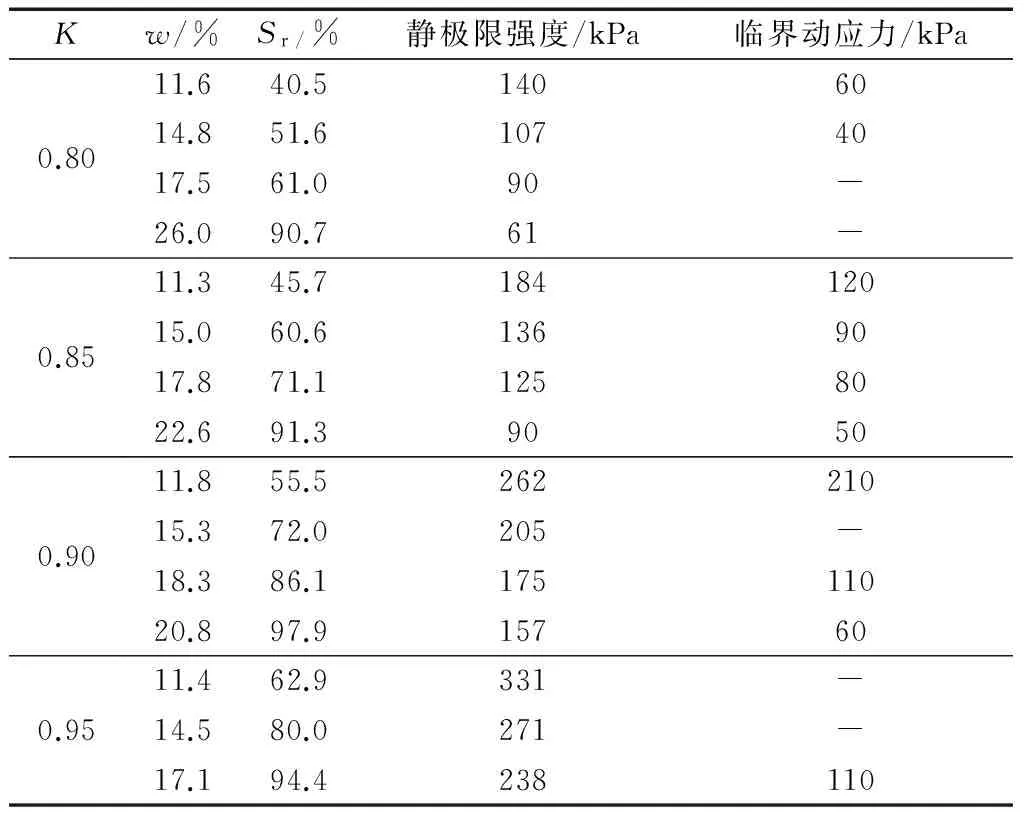
表3　不同压实系数与含水率条件下试样的强度

1.2.2路基土的累积塑性变形

图1为循环荷载下试样的2种典型应变累积曲线. 可以看出，每一次加卸载下土体变形由累积应变和弹性应变两部分组成. 对于变形稳定试样，在较少次数的循环加载后累积变形即可达到稳定；相反，对于破坏试样，累积变形随循环加载次数一直增大直至试样最终破坏. 因此，可以推断：还存在一个介于稳定和破坏之间的临界状态[12]，即试样的累积变形随循环加载既不趋于稳定，也不发生破坏.

图2为试样轴向累积塑性应变εp与动应力σd关系的典型曲线. 图2a对比了K=0.85时不同Sr下的试验结果，图2b对比了w=wopt时不同K下的试验结果. 可以看出，随着σd增加，εp增大；当σd小于一定水平时，εp缓慢增长，而当σd超过一定水平时，εp迅速增大直至破坏. 在相同σd水平下，饱和度增加或压实系数降低，εp增大，且饱和度越大或σd水平越高时，εp的增长速率越大.

a 动应力-轴向应变关系

b 轴向应变累积历史

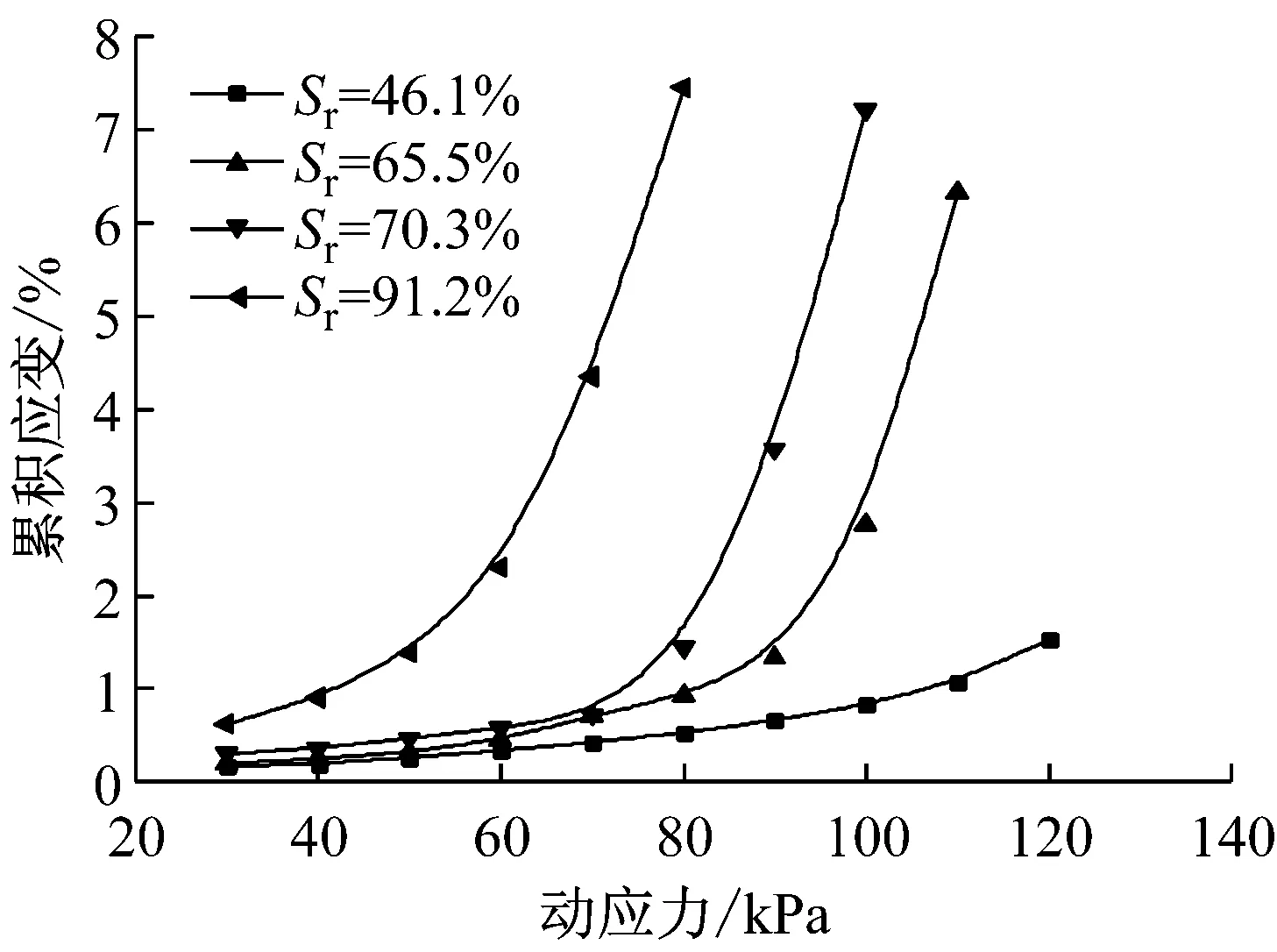
a 饱和度的影响

b 压实系数的影响

采用Monismith指数模型εp=ANb(A和b为试验参数)对不同动应力、压实系数、饱和度状态下εp与N的关系曲线(图1b)进行拟合，得到不同试验条件下的A,b值. 再以σd与土的静极限强度qs之比r(r=σd/qs)作为横坐标，分别给出A,b与r的关系，如图3所示. 通过比较发现，A,b与r分别采用指数方程和直线方程拟和效果最好.

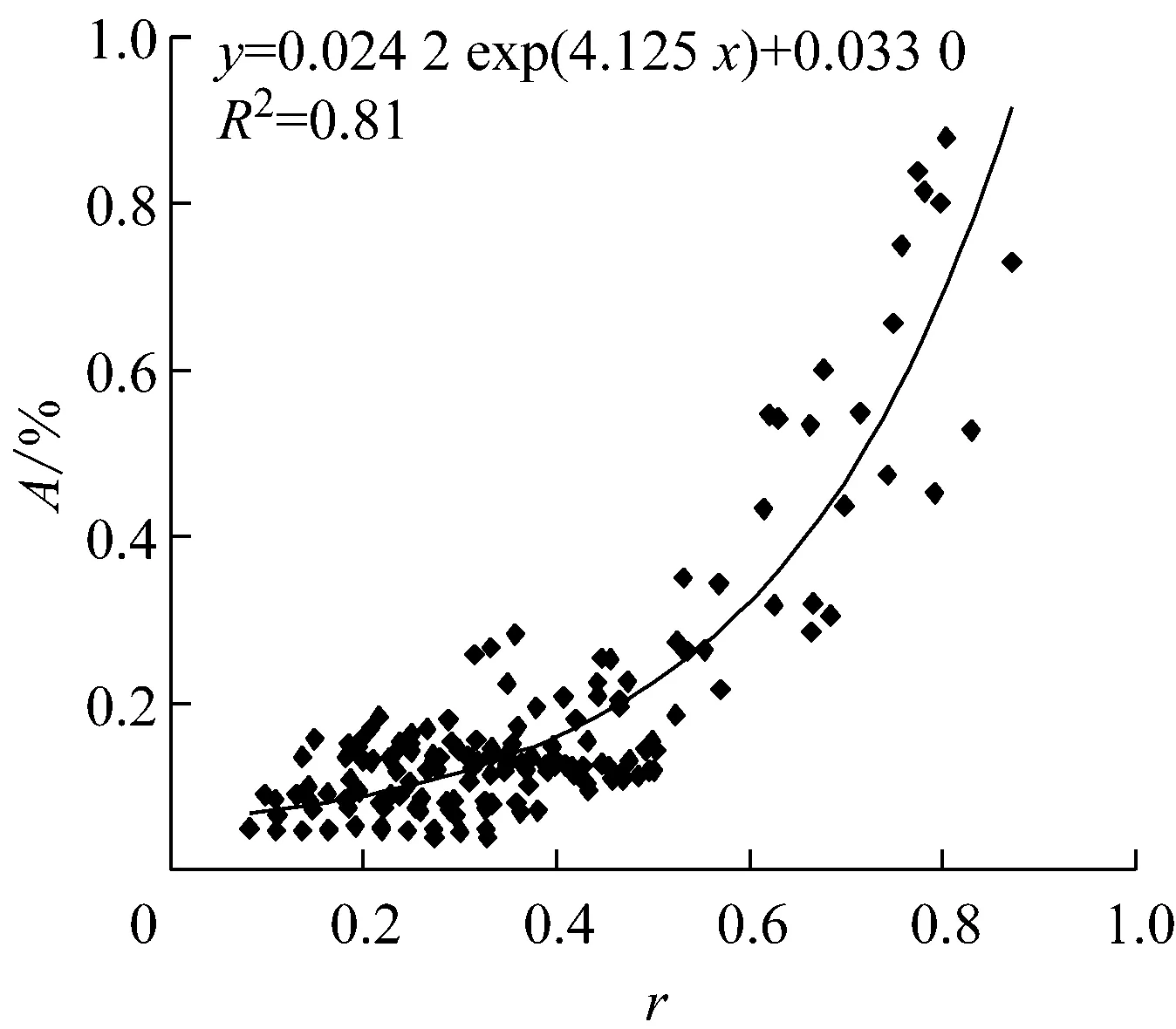
a A-r关系

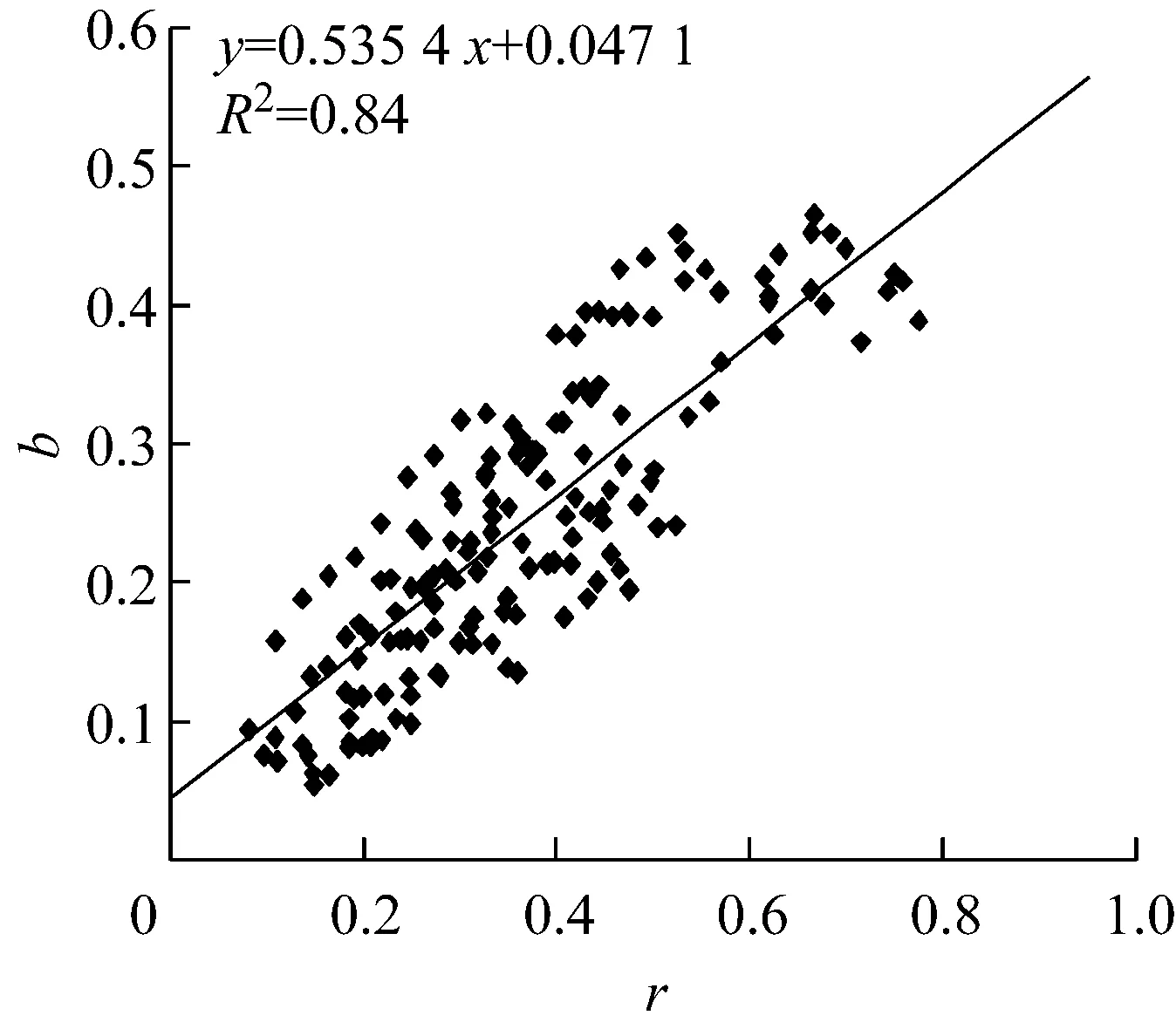
b b - r关系

至此，列车循环荷载作用下黄河冲积粉土路基土的εp可采用下式进行预估.

(1)

1.2.3临界动应力

取εp与σd关系曲线上的拐点作为试样的临界动应力，如图2所示，该应力水平是区分试样变形稳定和破坏的分界点. 表3列出试样在不同压实系数、饱和度状态下的临界动应力. 以K为0.85, 0.90的试样为例，图4给出临界动应力与饱和度关系的典型曲线，图中R为拟合直线的相关性系数. 可见，路基土饱和度增大，临界动应力线性递减，对于相同饱和度的试样，压实系数高，临界动应力高.

图4　临界动应力与饱和度关系的典型曲线

图5给出试样的临界动应力与静极限强度的关系. 表明，临界动应力与静极限强度的比值分布为0.360 4～0.606 1，两者的线性拟合系数为0.509 6，说明黄河冲积粉土路基土的临界动应力约为静极限强度的50%，这与其他研究结论一致[12].

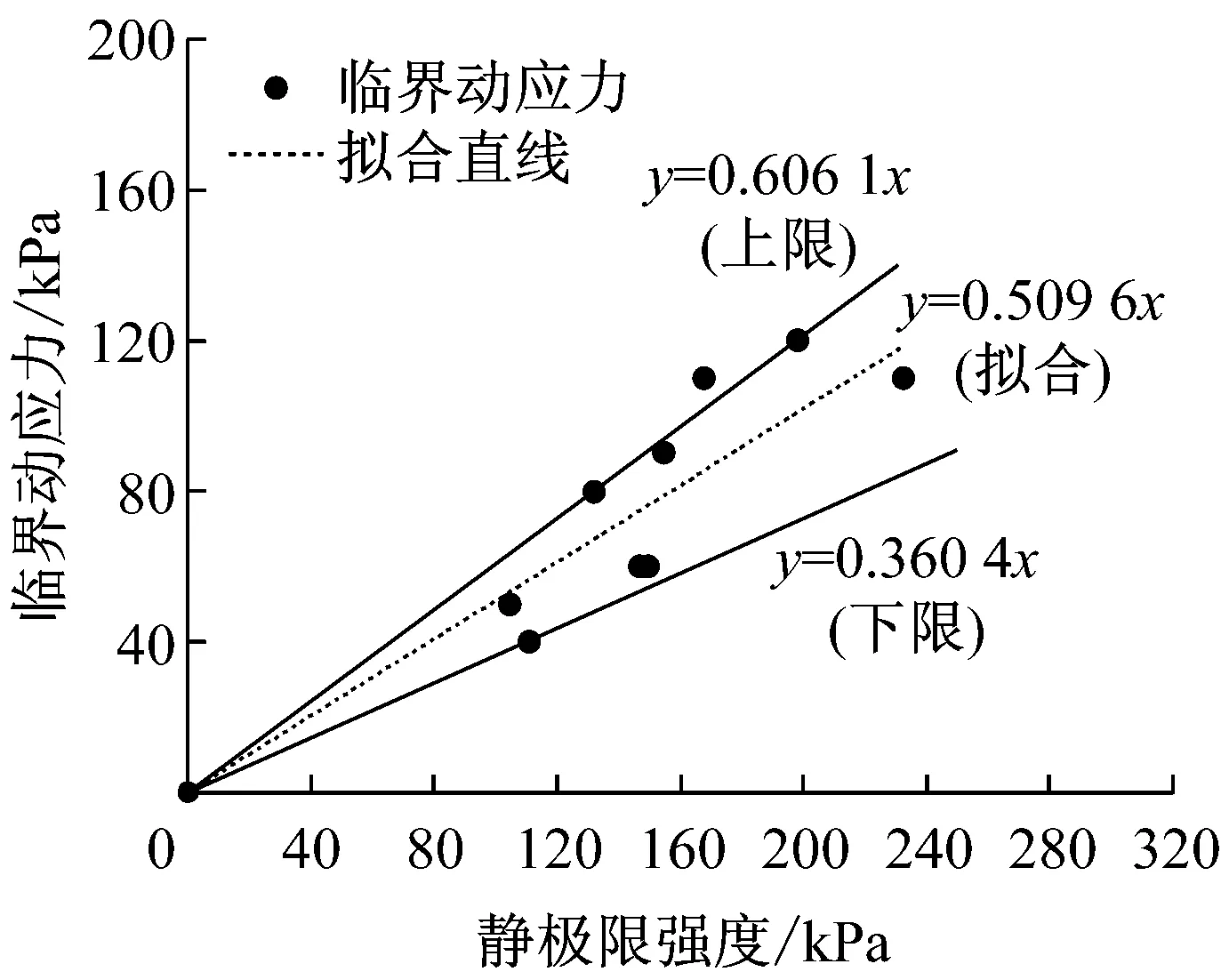
图5　临界动应力与静极限强度的关系

2重载条件下路基的动力稳定性分析

2.1重载下路基的荷载特征

计算分析思路为：将轨道沿纵向简化为连续弹性支承梁模型，求得车辆移动荷载下钢轨与轨枕之间的接触压力；然后，假设轨枕压力均匀分布在轨枕两端长度范围内，求得道床顶面荷载；通过建立道床-路基简化的平面动力有限元模型，模拟分析路基动荷载特征，详细分析思路见文献[8].

根据连续弹性基础梁理论，单个轮载作用下单根轨枕上的反力Fi为

(2)

将列车荷载简化为一系列常力Pw以匀速v在钢轨上移动，车辆和轨道相互作用的动力效应通过冲击系数来反映, 则在多轮载同时作用下，该轨枕的反力F为

(3)

式中：α为速度系数，β为偏载系数，取值见文献[8]；n为轮载数. 假设轨枕压力均匀分布在轨枕长度为e的范围内，则道床顶面压力σb为

(4)

式中：b为轨枕宽度，取0.28 m；e取1.1 m.

根据既有线路基特点，将路基等效成均一材料，这种处理方式并不会对路基动应力计算结果有实质影响[7]. 考虑简化，建立单线道床-路基动力有限元平面分析模型，模型尺寸参照《铁路路基设计规范》[13]，取路基面宽度7.9 m，路肩宽度0.8 m，路拱横坡4%，路基边坡坡度1∶1.5，道床边坡坡度1∶1.75；道床、路基和地基各层的计算厚度见表4. 模型参数依据现场调查数据和相关土工试验结果取值[11]，如表4所示.

表4　动力有限元分析计算参数

式(2)、式(3)中车辆和轨道参数参见文献[8]. 对列车轴重分别为23，25，27，30t、行车速度为80 km·h-1的4种工况下路基的动荷载特征进行模拟，图6得到不同轴重下路基动应力沿深度的分布曲线. 可见，路基面动应力幅值在60～80 kPa，随着轴重增加，路基面动应力幅值线性递增. 将路基面动应力幅值以单位轴重进行归一化处理，得到动应力幅值平均值σd, avg=2.6P，与实测数据接近[1,7]. 同时，路基动应力在基床范围内衰减速度较快，到基面下2.5 m动应力约为基面的50 %，计算的衰减规律较实测的衰减速度稍慢，这与计算时采用平面有限元模型有关. 从衰减曲线来看，轴重大小对动应力的衰减规律基本没有影响.

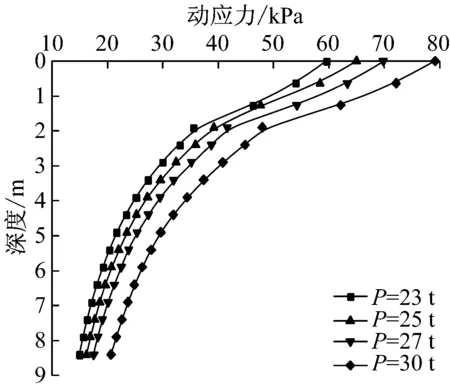
图6　重载下路基的动应力分布曲线

2.2路基的长期动力稳定性

对比图6和表3分析，假定路基处于最不利含水率(接近饱和)的极端情况，可以看出，当P=23t时，基床表层的最大动应力与压实系数K=0.90的路基土的临界动应力接近，基床底层的最大动应力低于K=0.90的路基土的临界动应力，但高于K=0.85的路基土的临界动应力. 同样地，当P=25t时，基床表层的最大动应力高于K=0.90的路基土的临界动应力，但低于K=0.95的路基土的临界动应力；基床底层的最大动应力与K=0.90的路基土的临界动应力接近. 而当P≥27t时，基床表层和底层的最大动应力均高于K=0.90的路基土的临界动应力，但低于K=0.95的路基土的临界动应力. 对于路基本体，在不同轴重下的最大动应力与K=0.85的路基土的临界动应力相当.

可见，在既有铁路重载条件下，应提高路基的压实系数以增大其临界动应力水平，从而适应路基动荷载的变化. 然而，临界动应力只是区分土体变形稳定与破坏的分界点，即使路基中动应力低于土体的临界动应力，路基不发生破坏，也可能产生了不能接受的永久变形. 因此，对于以变形控制为目的的铁路路基而言，还需对重载下路基的动力附加变形进行分析，以评估路基的长期动力稳定性.

由式(1)可知，列车荷载作用下路基的动力附加变形s的计算关键在于确定列车荷载产生的σd. 三维空间下σd采用下式计算：

(5)

式中：J2为第二应力不变量，通过动力有限元分析求解出的6个应力分量确定. 从而，列车荷载作用下s可以通过εp在变形深度h积分得到为

(6)

2.2.1路基动力附加变形与列车轴重的关系

图7为不同K下路基动力附加变形s与列车轴重P的关系曲线，假设路基处于最优含水率，取列车荷载循环次数N=106. 从图7可以看出，s与P的关系受K的影响. 对于不同K的情况，当P>27t时，s随P的变化速率明显加快.

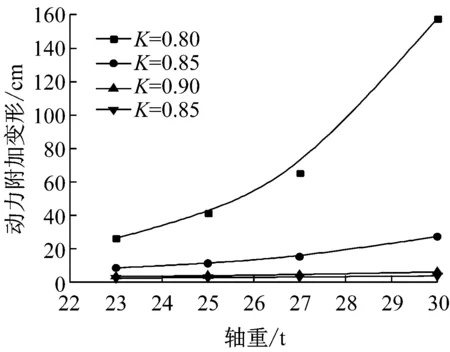
图7　最优含水率下路基动力附加变形与列车轴重的关系

对于图7的分析工况(最优含水率)，当K=0.80时，s随P的增加迅速增长且达到破坏，这是由于K=0.80时，路基土的临界动应力仅与23t轴重下路基的动荷载幅值相当，当P增大时，路基动荷载幅值均超过K=0.80时路基土的临界动应力. 当K≥0.85时，路基土的临界动应力均高于各轴重下路基的动荷载幅值，因此s并不迅速增长而产生破坏，而是随着P增加以较缓幅度上升；但是，从变形量来看，K=0.85时，27t与30t轴重下路基仍分别产生约15 cm和27 cm的动力附加变形；只是当K≥0.90时，各轴重下s不超过10 cm. 这再次说明，对于以变形控制为目的的铁路路基而言，仅根据临界动应力不足以评估路基的长期动力稳定性.

考虑到路基的天然含水率一般高于其最优含水率(表1), 图8给出了不同饱和度Sr下s与P的关系，图中对比了K=0.90和0.95的计算结果.

从图8可以看出，Sr越高或K越低，s随P增加而增长的趋势越明显；同样地，对于不同Sr的情况，P>27t，s随P的变化速率明显加快. 对于图8的分析工况，当K=0.90且接近饱和时，由于试样临界动应力不大于各轴重下路基最大动应力，s随P增加迅速上升且破坏；而对其他Sr条件(低于饱和含水率)，虽然K=0.90时临界动应力高于各轴重下路基最大动应力，但路基可能产生过量的永久变形而影响其使用. 如，当Sr=86.1%、临界动应力为110 kPa但P为27t和30t时，s分别达到20.6 cm，40.0 cm. 只是当K≥0.95时，不同Sr条件下，s随P增加而增长较缓，且各轴重下的最大s不超过10 cm.

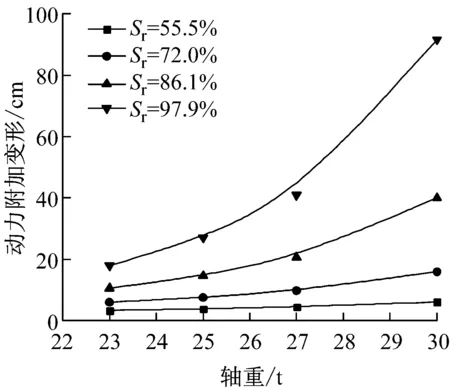
a K=0.90

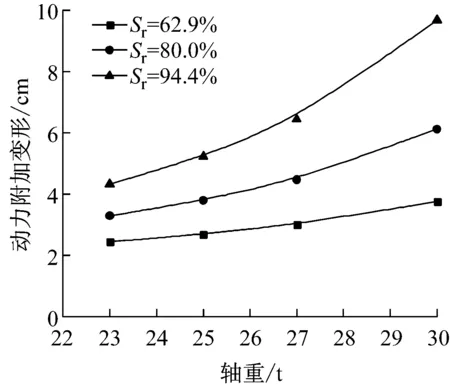
b K=0.95

2.2.2路基动力附加变形与轴载作用次数的关系

为探讨重载下s随N的变化趋势和变形达到的稳定时间，图9给出了不同P，K下s与N的关系曲线，假定路基处于最优含水率的情况. 从图中可以看出，K=0.90时的s均小于K=0.85时的s，即使较大的P作用在K=0.90的路基上；且K=0.90时，不同P下s在相对较短的加载次数内趋于稳定，而K=0.85时，不同P下s随加载次数的增加均不断增长，P越大，s的增长速率越大，且趋于稳定的时间越长. 特别地，当P=30t时，s随N的增长速率远大于其他轴重情况下，如，对于K=0.90，不同轴重下100万次加载和1 000万次加载的s相差37%～53%，变形绝对量仅相差1.2～3.2 cm；而对于K=0.85，不同轴重下100万次加载和1 000万次加载s相差64%～99%，变形绝对量相差5.4～27 cm. 因此，在重载条件下，提高路基压实系数(或强度)能显著减少路基变形量和变形稳定的时间.

图9　路基动力附加变形与轴载作用次数关系典型曲线

2.2.3路基动力附加变形的影响深度

为探讨重载下s的影响深度，图10以K=0.85、最优含水率为例，给出了不同P下s沿路基深度的分布曲线，其他计算条件下的结果与图10的规律类似. 可见，各轴重下s随深度迅速减小，至路基2.5 m(即基床厚度)以下，各轴重下路基的总沉降基本相当，且最大值仅约为2 cm. 特别地，s随P增加显著增大的深度范围约为1.0 m. 因此，重载下应主要关注路基基床产生的动力附加变形. 如在本计算工况中，列车轴重从23t变化到25t，27t和30t，路基面的总沉降分别增长32.5%，79.7%和222.9%，但路基2.5 m深度处的沉降分别仅增长8.2%，17.7%和41.8%，且该深度处的沉降仅为路基面总沉降的8.5%～19.4%.

图10　路基动力附加变形沿深度分布的典型曲线

3结论

(1) 对于路基压实系数低、饱和度高的情况，轴重增加，路基动力附加变形迅速增大，且当轴重超过27t，路基变形随轴重的变化速率明显加快；但是，当路基压实系数大于一定条件，轴重增加对路基的变形影响较小，对于本文的分析工况，路基处于最优含水率且压实系数超过0.90或者路基处于饱和含水率且压实系数超过0.95的2种情况，轴重增加对路基的变形影响均较小，且最大附加沉降不超过10 cm.

(2) 路基压实系数(或强度)较高，不同轴重下路基变形均可在相对较短的加载次数内达到稳定；反之，路基变形随加载次数增加不断增长，且轴重越大，变形的增长速率越大，趋于稳定的时间越长；在轴重为30t时，路基变形随加载次数的增长速率远大于其他轴重情况下，因此，在重载情形下，提高路基压实系数(或强度)能显著减少路基的变形量和变形达到稳定的时间.

(3) 在重载情形下，路基动力附加变形的影响深度主要在2.5 m范围内，且显著影响深度范围约为1.0 m，因此，重载下应主要关注路基基床的动力附加变形.

(4) 在重载情形下，即使路基中动应力低于土体的临界动应力、不发生破坏，可能产生了不能接受的永久变形. 因此，对于以变形控制为目的的铁路路基而言，需对重载下路基的动力附加变形进行分析，并结合路基的沉降控制要求，评估路基长期动力稳定性.

本文仅以一种典型的路基土为例，结合室内动三轴试验和列车荷载下路基动应力、动力附加变形的计算，分析了重载下不同物理状态的既有铁路路基长期动力稳定性的影响因素和规律，对类似工程具有参考意义. 然而，为深入研究和评估既有铁路开行大轴重列车路基的长期稳定性，需结合路基现场状态的检测和调查、路基土动力特性试验、重载下路基动应力测试和计算、重载铁路运量等，对路基动力附加变形进行分析，进而提出满足沉降要求的路基结构和参数.

参考文献:

[1]叶阳升, 蔡德钩, 张千里. 重载铁路路基关键问题探讨[C]//铁路重载运输货车暨工务学术研讨会论文集. 北京:中国铁道出版社, 2011:51-55.

YE Yangsheng, CAI Degou, ZHANG Qianli. Key issues on railway subgrade under heavy axle load train [C]// Conferennce Prceeding of Seminar on Railway Heavy-Haul Transport and Engineering. Beijing: China Railway Press, 2011:51-55.

[2]王立军.重载铁路路基评估的试验研究[D].北京:中国铁道科学研究院, 2005.

WANG Lijun. Test research of subgrade assessment of heavy load railway [D]. Beijing: China Academy of Railway Sciences, 2005.

[3]Li D Q, Hyslip J, Sussmann T,etal. Railway geotechnics [M]. Boca Raton: Chemical Rubber Company Press, 2015.

[4]Indraratna B, Nimbalkar S, Rujikiatkamjorn C. From theory to practice in track geomechanics-Australian perspective for synthetic inclusions [J] .Transportation Geotechnics, 2014, 1:171.

[5]Gräbe P, Shaw F. Design life prediction of a heavy haul track foundation [J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2010, 224(S1): 337.

[6]聂如松, 冷伍明, 杨奇. 既有重载铁路路基检测试验与状态评估[J]. 铁道工程学报, 2014, 194(11):20.

NIE Rusong, LENG Wuming, YANG Qi. Detection test and condition assessment on existing heavy hual railway subgrade[J].Journal of Railway Engineering Society, 2014,194(11):20.

[7]肖世伟,雷长顺. 重载铁路路基荷载特征和路基动力响应分析[J]. 铁道工程学报,2014,187(4):51.

XIAO Shiwei, LEI Changshun. Loading characteristics and dynamic response analysis of subgrade for heavy haul railway [J]. Journal of Railway Engineering Society, 2014,187(4):51.

[8]狄宏规, 冷伍明, 薛继连, 等.朔黄铁路重载扩能的路基强度评估[J]. 铁道学报, 2014,36(8):84.

DI Honggui, LENG Wuming, XUE Jilian, etc. Assessment of subgrade strength for transport capacity enlargement of shuo-huang heavy-haul railway[J]. Journal of the China Railway Society, 2014,36(8):84.

[9]Liu J K, Xiao J H. Experimental study on the stability of silt railroad subgrade with increasing train speed [J].Journal of Geotechnical and Geoenvironmental Engineering, 2010, 136 (6): 833.

[10]中国铁道科学研究院. 既有线提速200km/h非改建地段试验报告[R]. 北京: 中国铁道科学研究院, 2006.

China Academy of Railway Sciences. Experimental report of existing railway without reconstruction with train speed increasing to 200 km/h. Beijing: China Academy of Railway Sciences, 2006.

[11]肖军华，刘建坤，彭丽云，等. 黄河冲积粉土的干密度及含水率对力学性质影响[J]. 岩土力学，2008, 29(2):409.

XIAO Junhua, LIU Jiankun, PENG Liyun,etal. Effect of dry density and moisture content on behaviors of Yellow-River alluvial silt[J]. Rock and Soil Mechanics, 2008, 29(2):409.

[12]Xiao J H, Juang C H, Xu C J,etal. Strength and deformation characteristics of compacted silt from the lower reaches of the Yellow River of China under monotonic and repeated loading [J]. Engineering Geology, 2014, 178: 49

[13]中华人民共和国铁道部. TB 10001 铁路路基设计规范[S]. 北京: 中国铁道出版社, 2005.

Ministry of Railways of the People’s Republic of China. TB 10001 Code for design on subgrade of railway[S]. Beijing: China Railway Press, 2005.

收稿日期：2015-10-11

基金项目：国家“八六三”高技术研究发展计划(2007AA11Z116)；国家自然科学基金(51008158)；中央高校基本科研业务费专项资金

中图分类号：U213.1

文献标志码：A

Dynamic Stability of Existing Railway Subgrade under the Effect of Heavy Axle Load Trains

XIAO Junhua, GUO Pengfei, ZHOU Shunhua, DI Honggui

(Key Laboratory of Road and Traffic Engineering of the Ministry of Education, Tongji University, Shanghai 201804, China)

Abstract：In order to study additional cumulative deformation and dynamic strength stability of railway subgrade under effect of heavy axle load train for existing railway lines, typical subgrade soil was selected to conduct cyclic triaxial tests to obtain the variations of cumulative plastic deformation and threshold stress under various physical states and cyclic loading conditions. Consequently, the prediction formula of cumulative strain was established. On this basis, by dynamic finite element method and layer-wise summation method, dynamic stress and additional settlement of subgrade under heavy axle load were calculated. The conclusions are as follows: subgrade settlement rises rapidly with increasing in the axle load in conditions of low compaction or high saturation, and moreover, the settlement rises significantly when axle load exceeds 27t; but when the compaction coefficient is larger than a certain value, the increase of axle load has a smaller effect on subgrade settlement; the influential depth of additional settlement in subgrade under heavy axle load is mainly within 2.5m from subgrade surface, especially within 1.0m; under heavy axle load, subgrade may generate unacceptable permanent deformation even it meets the threshold stress condition. To reduce subgrade additional deformation and its duration under heavy axle load, the compaction coefficient or strength of subgrade should be improved.

Key words：existing railway subgrade; heavy axle load; threshold stress; additional dynamic settlement

第一作者： 肖军华(1980—)男，副教授，工学博士，主要研究方向为铁路路基. E-mail：jhxiao@tongji.edu.cn