基于自动生成策略的供水管网抗震优化算法

刘　威， 元宏伟， 徐　良

(1.同济大学 土木工程防灾国家重点实验室，上海 200092；2. 同济大学 土木工程学院，上海 200092；3. 北京市建筑设计研究院，北京 100045；4. 上海核工程研究设计院，上海 200233)



基于自动生成策略的供水管网抗震优化算法

刘威1,2， 元宏伟3， 徐良4

(1.同济大学 土木工程防灾国家重点实验室，上海 200092；2. 同济大学 土木工程学院，上海 200092；3. 北京市建筑设计研究院，北京 100045；4. 上海核工程研究设计院，上海 200233)

摘要：以管网年费用折算值为优化目标、管网拓扑结构与管径为优化参数、管网节点抗震可靠度为约束条件, 建立了供水管网抗震优化设计模型.基于自动生成策略，并结合环形管网判断方法，分别利用遗传算法、遗传-模拟退火算法和微粒群算法进行了供水管网的抗震拓扑优化分析.利用3种优化方法对2个典型供水管网进行了对比分析.对比分析表明，遗传-模拟退火算法具有最好的优化能力.

关键词：供水管网； 自动生成策略； 遗传算法； 遗传-模拟退火算法； 微粒群算法

生命线工程系统是指维系现代城市功能与区域经济功能的基础性工程设施系统[1].作为城市生命线系统的重要组成部分，城市供水管网对城市的日常运行和灾后抢险救灾具有重要意义.进行城市供水管网抗震优化设计，确保城市供水系统在地震中和地震后安全可靠运行，减少地震灾害的损失，加快灾后城市恢复的时间，是亟待解决的问题.在这方面的研究中，Chen等[2]首次以管网建设造价为优化目标，利用遗传算法并结合启发式管径优化算法进行了基于功能可靠度的供水管网抗震拓扑优化和管径优化研究.进而，李杰等[3]、邢燕等[4]分别利用模拟退火算法和遗传-模拟退火混合算法对供水管网进行了抗震拓扑优化设计.徐良等[5]以管网年费用折算值为优化目标、以管网拓扑结构与管段管径为优化参数、以管网节点最低可靠度为约束条件，建立供水管网抗震优化设计模型，并将微粒群算法应用到管网系统抗震优化问题中.上述研究都从一个初始经验管网出发来进行简化，优化结果对初始经验管网依赖很大.2010年，李杰等[6]首先提出了基于自动生成策略的供水管网抗震优化设计方法.这一方法只需要管网用户节点信息就可以生成满足抗震要求的供水管网，但这一方法在生成管线时不考虑实际工程背景，而是直接认为管线是连接管网节点的直线，与实际工程尚有差距.

在上述工作基础上，本文将供水管网所在区域的道路信息引入管网优化设计中，并结合环形网络判断方法，提出了新的自动生成网络拓扑结构的策略.基于此策略，本文利用遗传算法、遗传-模拟退火算法和微粒群算法进行了城市供水管网系统抗震拓扑优化分析，并结合算例进行了对比分析.

1供水管网的抗震优化模型

以城市供水管网拓扑结构和管径为优化参数、抗震可靠度作为约束条件、管网建造运营费用最小为设计目标来进行供水管网优化设计，可建立如下供水管网抗震优化模型[5]:

minW

(1)

式中：βmin为供水管网所有节点的抗震可靠度指标的最小值，可以采用文献[7]介绍的均值一次二阶矩方法来求解；β0为供水管网设计时允许的抗震可靠指标限值；W为供水管网的年费用折算值，可用下式表示[8]：

(2)

式中：p为管网的每年折旧和大修的百分率；T为管网建设投资偿还期，年；n为泵站数目；WPi为泵站i的单位运行电费指标，元·(m-3·s·m·年)；qi为泵站i的设计扬水流量，m3·s-1；hpi为泵站i的最大扬程，m；WN为管网造价，可用下式计算得到:

(3)

式中：lj为管线j的长度，m；dj为管线j的管径，m；a1，a2，a3为造价经验系数，可以分别取62.105 1，1 979.7，1.486[9]；γj为管线j的连通系数，铺设管线时取为1，不铺设时取为0；m为管网中管线的数目.

2供水管网自动生成策略

自动生成技术的含义是从某种已有拓扑结构(包括空白结构)出发，按照一定的规则，将单元增加到结构中去，并不断地进行调整，直至最后形成满足预先给定要求的拓扑构形为止.在供水管网抗震优化设计中，采用自动生成技术可以生成优化算法的初始种群.考虑到在实际工程中供水管网应尽可能沿道路延伸，本文将供水管网所在区域的道路信息引入管网优化设计中，建立了基于道路信息的供水管网自动生成策略.

相比于树状供水管网，环状供水管网有着更好的可靠性.因此，本文将环形管网生成方法引入自动生成策略中，实现了供水管网的优化设计.

2.1建立管网的初始信息

将管网所在区域的道路信息用道路节点间的路径来表示，同时将管网节点放置于路径之中.这样在初始状态下，管网信息由道路节点、道路节点间的路径以及管网节点信息组成.同时，根据实际情况可以给出道路节点以及管网节点间的路径长度.

2.2判断能否生成环形网

2.3管线生成规则

管线的生成规则为：①当管线两节点之间没有通过其他管网节点或只通过道路节点，则生成1条管线；②当两节点之间的管线通过其他管网节点，则以这些节点为端点生成多条管线.

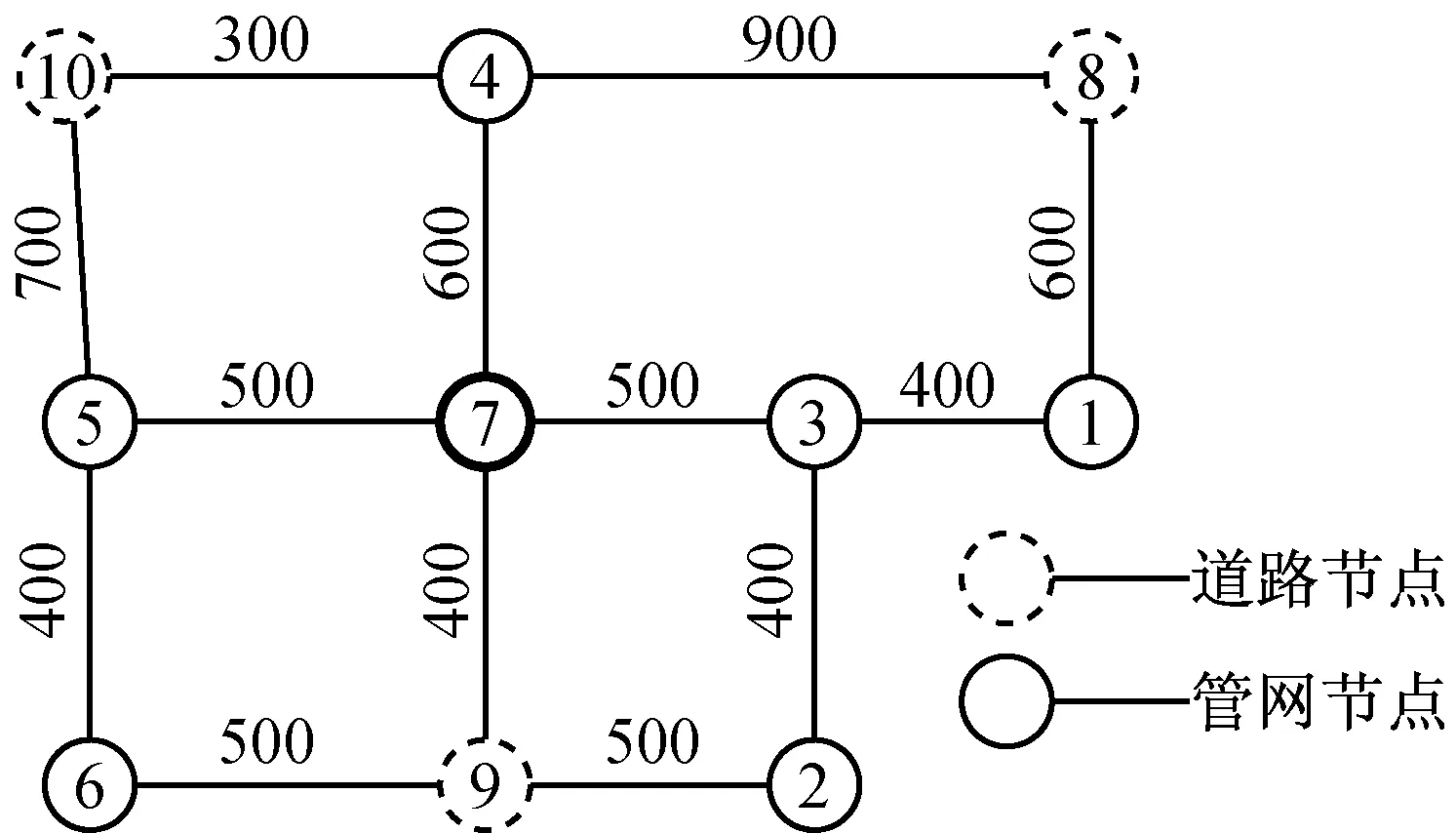
上述规则保证任意一条管线以节点为端点，中间不通过其他节点.以图1d中的网络为例(节点8，9和10为道路节点)，若节点7，5间生成管线，即为管线7-5，管线的连接方式为7-5，长度为500 m；若节点7，6间生成管线，管线的连接方式为7-9-6，由于9是道路节点，不是管网节点，故生成管线7-6，长度为900 m；若节点7，1间生成管线，管线的连接方式为7-3-1，由于节点3为管网节点，则生成管线7-3和3-1，长度分别为500 m和400 m.

2.4生成初始管网拓扑结构

在优化算法中，首先要生成一系列初始管网.在生成初始管网时，按照管网节点的编号顺序逐个遍历所有节点.对每个管网节点，生成它与其他节点之间的管线.生成方法为：对处于管网边缘的节点，利用Dijkstra算法[10]找出与其路径最短的3个节点；对处于管网中心的节点，找出与其路径最短的4个节点，同时以一定概率生成它们之间的管线.

a管网1b管网2

c 管网3

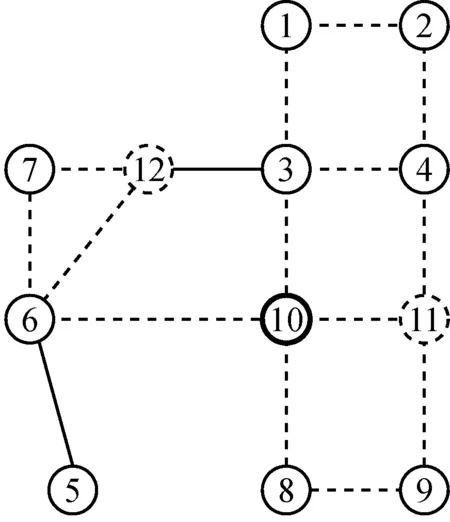
d 管网4

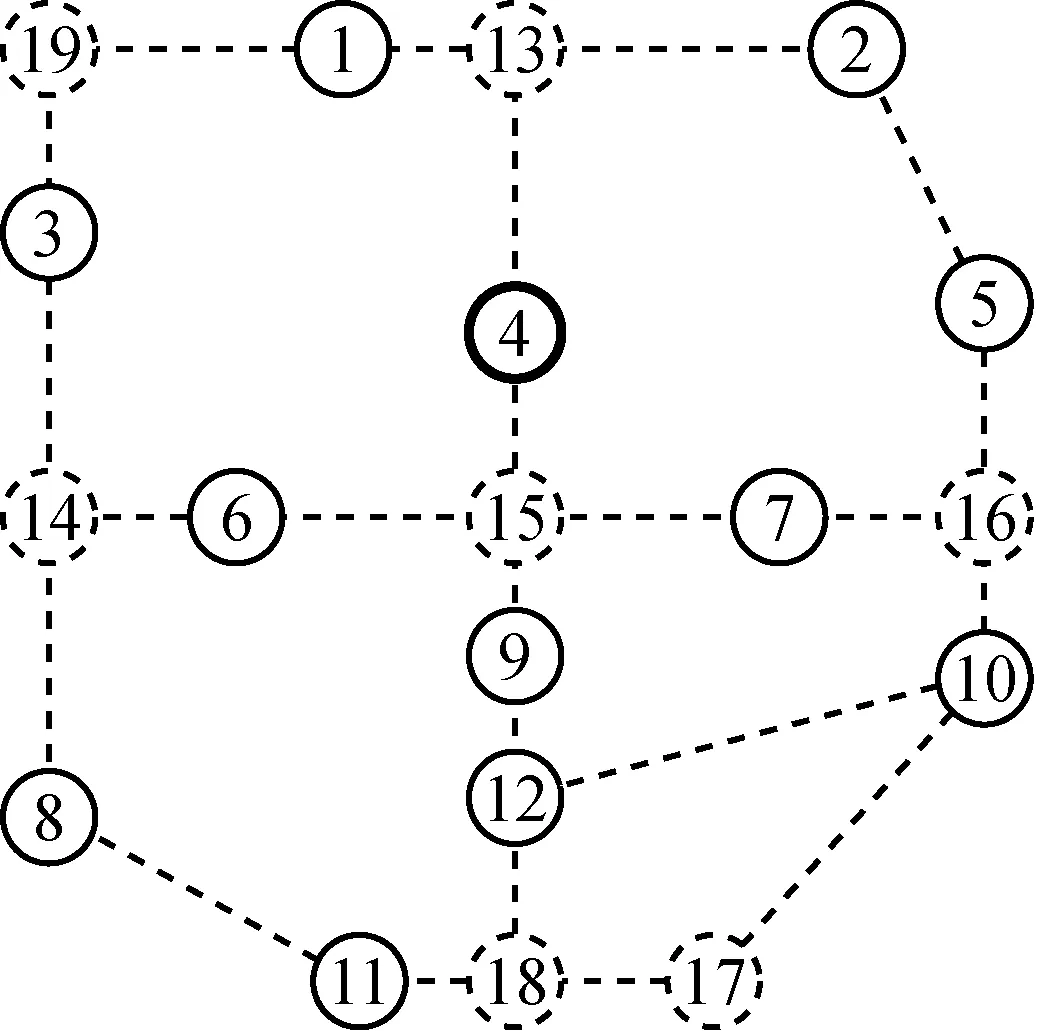
图2　待建供水管网

如图2所示待建供水管网，4为水源点，1-3和5-12为需水节点， 13-19为道路节点.以边缘节点1为例，如图3a所示，与其路径最短的3个节点为节点3，4和2.若节点1和3间生成管线，即为管线1-3，管线的连接方式为1-19-3.节点4为中间节点，如图3b所示，与其路径最短的4个节点分别为节点9，2，1和6.若节点4和2间生成管线，即为管线4-2，管线的连接方式为4-13-2；若节点4，9间生成管线，即为管线4-9，管线的连接方式为4-15-9.对每个节点进行一次操作，得到的一个可能的管网拓扑结构如图4所示.

2.5环状修补过程

需要指出的是，在环状管网设计过程中，可能会产生一些无意义的解，即：出现节点度为零的节点，从而造成1个管网断成2个或多个子网；或者生成的管网为非环形网.因此要对每一次生成的管网进行环状修补，修补过程如下：

(1)将初始管网个体中生成的一条管线暂时删除，同时暂时删除这条管线所经过道路的道路信息.

(2)对此个体在此道路信息下进行连通性修补.

a生成与节点1连接的管线b生成与节点4连接的管线图3 管网生成过程Fig.3 Processofnetworkgeneration图4 管网拓扑结构Fig.4 Networktopology

首先，采用广度优先搜索，判断生成的管网拓扑结构的连通性，若存在与水源点不连通的节点，则对其进行连通性修补.进行修补时，对每个与水源点不连通的节点按前述自动生成管线的方式来增加管线，即：对处于管网边缘的不连通节点，找出与其连接路径最短的3个与水源点连通的节点，若此时与水源点连通的节点数小于3，则找出所有与水源点连通的节点；对处于管网中心的不连通节点，找出与其连接路径最短的4个与水源点连通的节点，若此时与水源点连通的节点数小于4，则找出所有与水源点连通的节点.同时，以一定概率生成它们间的管线.

(3)将暂时删除的那条管线和道路信息还原.

(4)对个体中每条已生成的管线依次重复步骤(1)～(3).

(5)对修补后的个体判断是否为环状网.若非环状网，则删除此个体，重新生成.

图5是对图4进行环状修补后得到的环状管网.

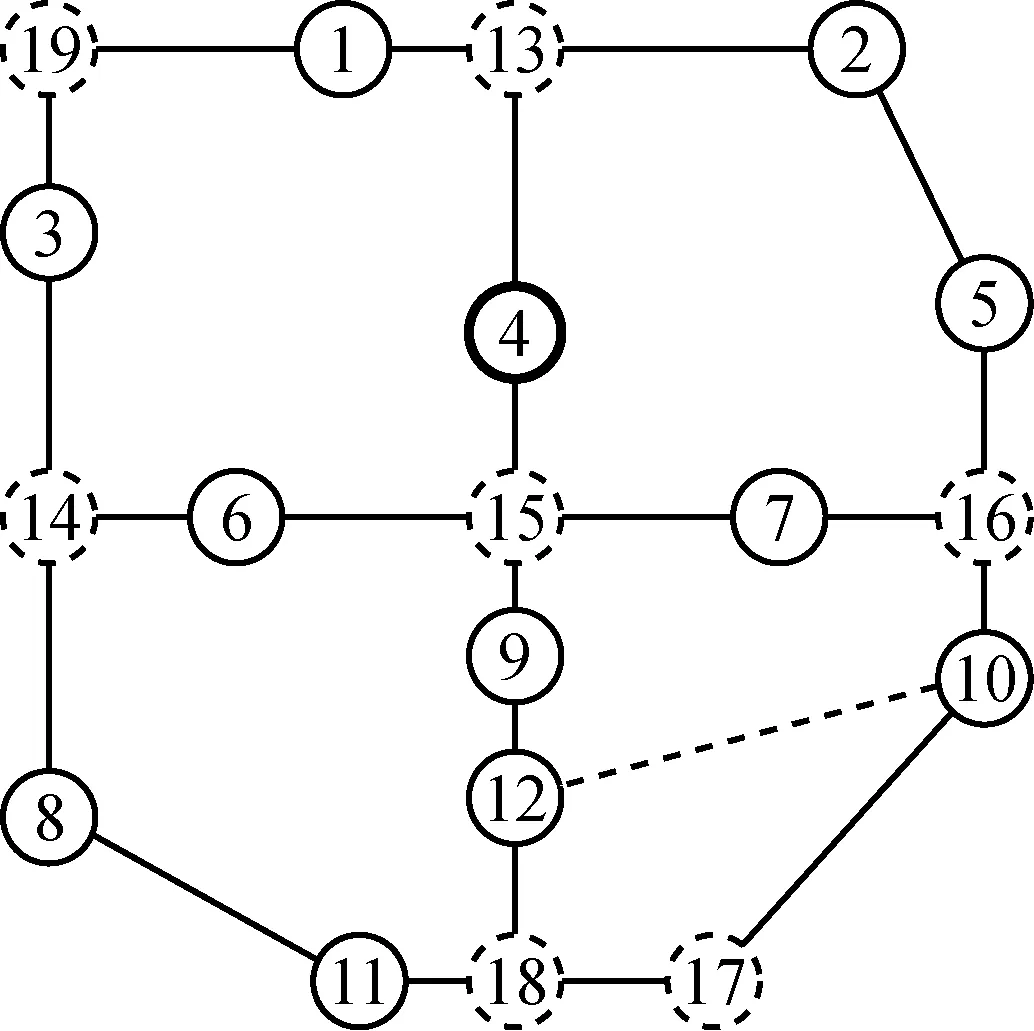
图5　修补生成的环状网

3基于自动生成策略的优化算法在供水管网抗震优化中的应用

在管网优化过程中，可以采用生物进化的原则构造管网拓扑优化问题的优化算法.

3.1遗传算法

遗传算法是借鉴生物进化原则在20世纪70年代初期由美国密西根大学的Holland[11]教授提出的一种自适应并行全局优化概率搜索算法.其计算步骤包括编码、生成初始种群、个体评价、选择操作、交叉操作、变异操作和收敛性判断等.

(1)编码.把一个问题的解从其解空间转换到遗传算法所能处理的搜索空间的过程称为编码.假定一根管线管径可取100，150，200，250，300，350，400，450，500 mm，则对应的基因可取1，2，3，4，5，6，7，8，9，而基因取0值则表示这根管线不铺设.所有优化参数对应的基因按照指定的次序排列起来，就构成一条染色体.在管网拓扑优化模型中一个染色体对应管网的一种拓扑结构方案.多条染色体构成遗传算法的一个种群.

(2)生成初始种群.初始种群的生成由自动生成策略来实现.

(3)个体评价.通过计算个体适应度来评价个体，这里定义个体s(个体也即优化的一个解)的适应度函数为

(4)

式中：M为预先指定的一个较大的数值；W(s)为个体s对应管网的年费用折算值；P1(s)，P2(s)为惩罚函数，可采用下式来计算惩罚函数：

徐晓春等(2004)对民乐铜矿区的辉铜矿化英安斑岩等样品进行了Sm-Nd同位素年龄测定，等时线年龄为228±56 Ma，说明与该套中三叠世火山岩地层的时代属于同一时代。

(5)

P2(s)=

(6)

(4)选择操作.选择操作是根据计算得到的个体适应度选择优胜的个体进入下一代，并淘汰劣质个体.本文采用最佳个体保存方法和适应度比例方法.最佳个体保存方法是将上一代最优的个体直接选择进入下一代，并将最优个体从群体中删除; 适应度比例方法即按群体中各个体的适应度来确定个体被选择的概率.当选择出来的个体达到规定的数目时，选择操作结束，本文取为群体个体总数的1/3.

(5)交叉操作.交叉操作是遗传算法中的重要操作之一，其以一定的交叉概率把2个父代个体的部分结构加以替换重组从而生成新个体.这里采用单点交叉方法，其操作过程是在个体串中随机设定一个交叉点，对随机选择出来的2个父代个体在该点前的部分结构进行互换，从而生成2个新个体.这里对每一次交叉操作生成的新个体进行环状网判断及相应的环状修补.

(6)变异操作.变异操作是指以一定的变异概率将某个染色体编码串中的基因用其他等位基因进行替换.这里对交叉获得的新管网通过对其中的管线以一定的概率用其他直径的管线代替来形成一个新的个体.在这过程中，为了引导管网个体向较好的方向发展，对满足最小可靠度指标要求的节点，以一定概率删除以此节点为端点的管线；对不满足最小可靠度指标要求的节点，按生成管线的方式以一定概率生成与其他节点连接的管线.对新个体进行环状网判断及相应的环状修补.

(7)收敛判断.本文采用固定迭代次数作为算法终止条件.

3.2遗传-模拟退火算法

将模拟退火算法[12]嵌入到遗传算法中发展出来的遗传-模拟退火混合算法[13]可有效地增强遗传算法的搜索能力.混合算法的计算过程与遗传算法基本一样，只是在变异操作时采用模拟退火操作.下面结合管网优化问题来介绍模拟退火操作的步骤.

3.2.1目标函数

模拟退火操作针对交叉操作得到的解来进行，每次选择一个解作为当前的初始解，然后对当前解进行随机扰动产生一个新解，根据式(7)确定接受新解的概率P，也即用解s2代替解s1的概率.

(7)

式中：t为当前的温度；f(s)为解s的目标函数.

(8)

式中：W(s)为解s对应管网的年费用折算值；P3(s)为惩罚函数，可以采用下式来计算：

(9)

式中：b1，b2为常数，其值的大小需要根据具体的管网来确定.

3.2.2随机扰动模型

3.2.3温度参数的控制

温度参数是模拟退火过程中最关键的参数，主要包括起始温度的选取、温度的下降方法、每一温度迭代次数的确定等.

一般采用t0=Cδ来估计初始温度.其中，C为通过试算得到的一个充分大的数，δ=Wmax-Wmin，Wmax，Wmin为父代群体中个体年费用折算值的最大值和最小值.

模拟退火操作要求温度下降到零，整个系统以概率1收敛到全局最优解.本文所用温度下降的方法为tr′+1=αtr′，其中：r′为模拟退火操作的计算代数；α为降温速率，0<α<1，α越接近于1温度下降越慢，这种方法简单易行，它的每一步以相同的比率降温.

本文采用固定长度法来给定每一温度的迭代长度.

3.3微粒群算法

微粒群算法[14]是通过模拟鸟群的捕食行为而建立的优化算法.在微粒群算法中，设待优化问题的解在一个d维的搜索空间中，群体中的第s个微粒位置表示待优化问题的一个解，可表示为一个d维矢量，Xs=(xs1,xs2,…,xsd)T；微粒s的速度表示其位置的改变，可用Vs=(vs1,vs2,…,vsd)T来表示.当前群体的最好位置的微粒l用Kl=(kl1,kl2,…,kld)T表示，整个演化过程中历史最好位置的微粒g用Kg=(kg1,kg2,…,kgd)T表示.则微粒群中，对每一代微粒s的第u维的进化方程为

(10)

(11)

式中：γ为惯性权重，取值越大全局搜索能力越强，取值越小局部搜索能力越好；r为进化代数；R1()和R2()为2个随机函数，产生0～1之间的随机数；c1，c2为加速度常数，取较大值可以拓展微粒的搜索空间，取较小值则可提高微粒的搜索精度.

将微粒群算法应用到管网抗震优化设计中时，每个微粒的位置对应一个管网结构方案，即问题的一个解.其编码方式与遗传算法相同.在进化过程中，当位置矢量中某一维的值小于零时，则取零；当其值大于最大管径编码值时，则取最大管径编码值；处于两者间时，则选择与其最接近的管径编码值.

管网抗震优化问题的优化目标是为了获得在满足节点最低抗震可靠度条件下管网最低的年费用折算值，于是对不满足约束条件的解，通过增加年费用折算值对其惩罚.解s的适应值函数取为

(12)

式中：P4为惩罚函数，可取足够大的常数.

管网抗震优化的微粒群算法的步骤如下：①微粒群个体的初始位置由自动生成技术来实现，并随机产生初始速度；②计算每个微粒的适应值，对不满足约束条件的微粒采用罚函数进行处理；③对每个微粒，将其适应值与其当前群体最好位置的适应值进行比较，若较好，则将其作为当前群体最好位置；④将当前群体最好位置的适应值与整个演化过程中历史最好位置的适应值进行比较，若较好，则将其作为历史最好位置；⑤分别对每个微粒的各维的速度和位置进行更新，并对无效的管网结构进行修补，如未达到一个预设的最大迭代数，则返回步骤②.

3.4供水管网抗震优化过程

城市供水管网系统的抗震优化设计过程如图6所示.整个设计过程依托于优化算法的大框架，将自动生成策略嵌入此大框架之中，进而完成整个设计过程，最终给出优化的设计管网.

图6　供水管网抗震设计过程

4实例分析

4.1实例1

图7为一个20个节点的待建供水管网，其中节点1～19为用户节点，20为水源点，21～33为道路节点，虚线给出了待建供水管网所在区域的道路分布状况.考虑地震烈度为8度进行管网抗震优化设计.管材为铸铁.约束条件取最低可靠度指标为0.84(对应节点最小可靠度0.80).根据工程实际，选定管网中管线的管径种类和管径值，分别为160，200，250，300，350，400，450，500，550 mm 这9 种，对应的管径编码取为1，2，3，4，5，6，7，8，9.取种群规模为60，迭代次数为50，管线生成概率取0.9，各优化算法基本参数如下.

图7　实例1待建供水管网

遗传算法：交叉概率采用动态自适应算法来确定，即：若个体适应度大于群体的平均适应度，则交叉率取0.90；反之，则交叉率取0.99.变异概率取为0.2.

遗传-模拟退火算法：交叉概率同遗传算法，初始温度为100度，当前循环温度为上一代的0.4倍，内循环次数为10次.

微粒群算法：惯性权重γ从0.9至0.4线性减小，加速度常数c1和c2均从1.5至0.4线性减小.

利用前述3种方法分别对待建管网进行抗震优化设计.图8给出了3种方法的供水管网优化方案.表1给出了3种方法所得优化方案的管网年费用折算值，表2给出了3种优化算法给出的优化结果中各个节点的可靠度指标.从表1可以看出，遗传-模拟退火算法的费用最低，微粒群算法次之，遗传算法最高，但遗传算法与微粒群算法的费用差别不大.从表2可以看出，遗传-模拟退火算法得到的结果中节点可靠度指标最高，平均值达到2.012 3；遗传算法次之，节点可靠度指标平均值为1.504 2；微粒群算法最低，为1.343 9.因此，遗传-模拟退火算法得到的优化结果年费用折算值低，节点可靠度指标均值高，表现最好.遗传算法虽然年费用折算值比微粒群算法略高，但是得到的节点可靠度指标均值比微粒群算法好.因此本例中，遗传-模拟退火算法表现最好，遗传算法和微粒群算法表现相当.

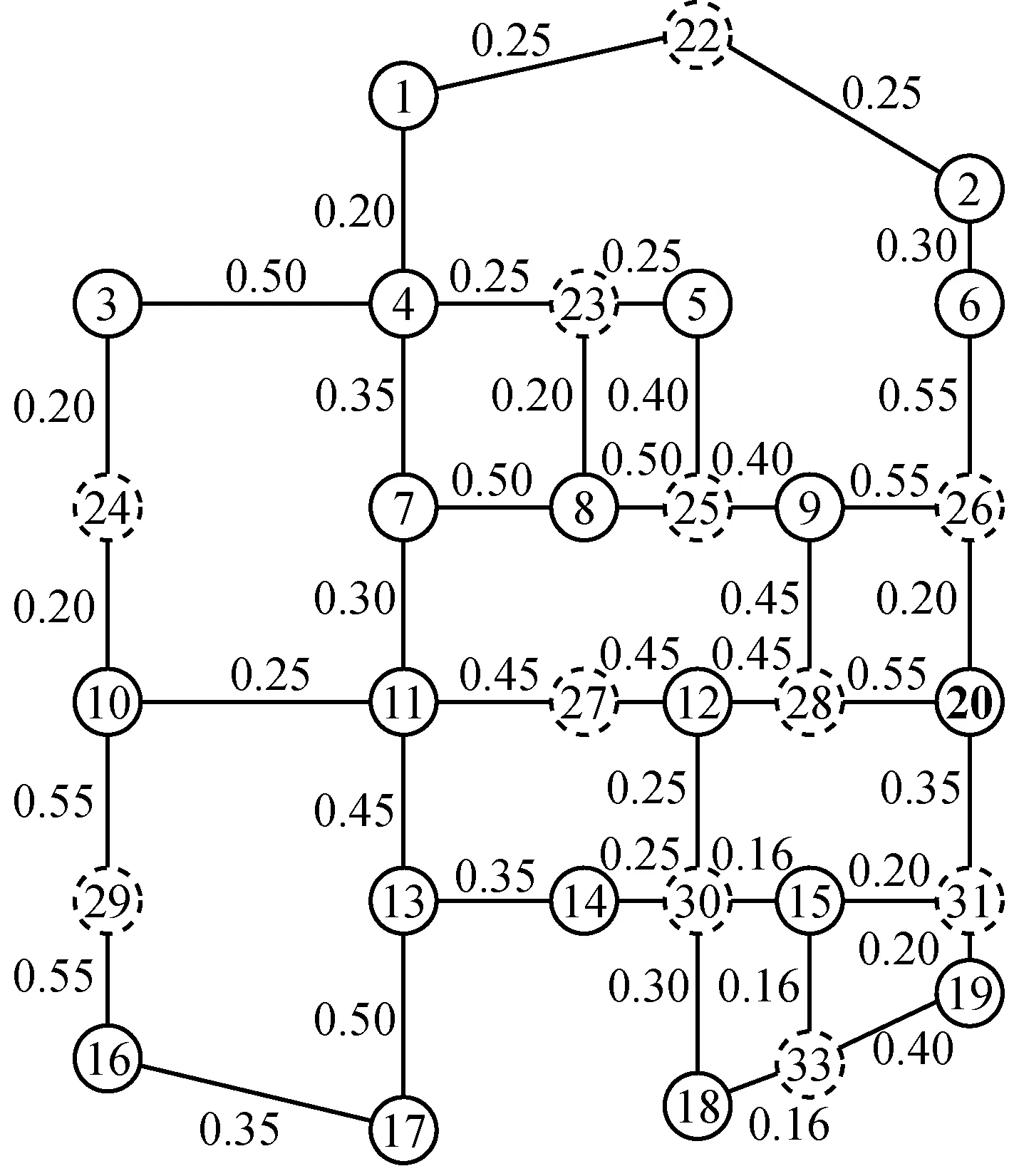
a 基于微粒群算法的管网优化方案

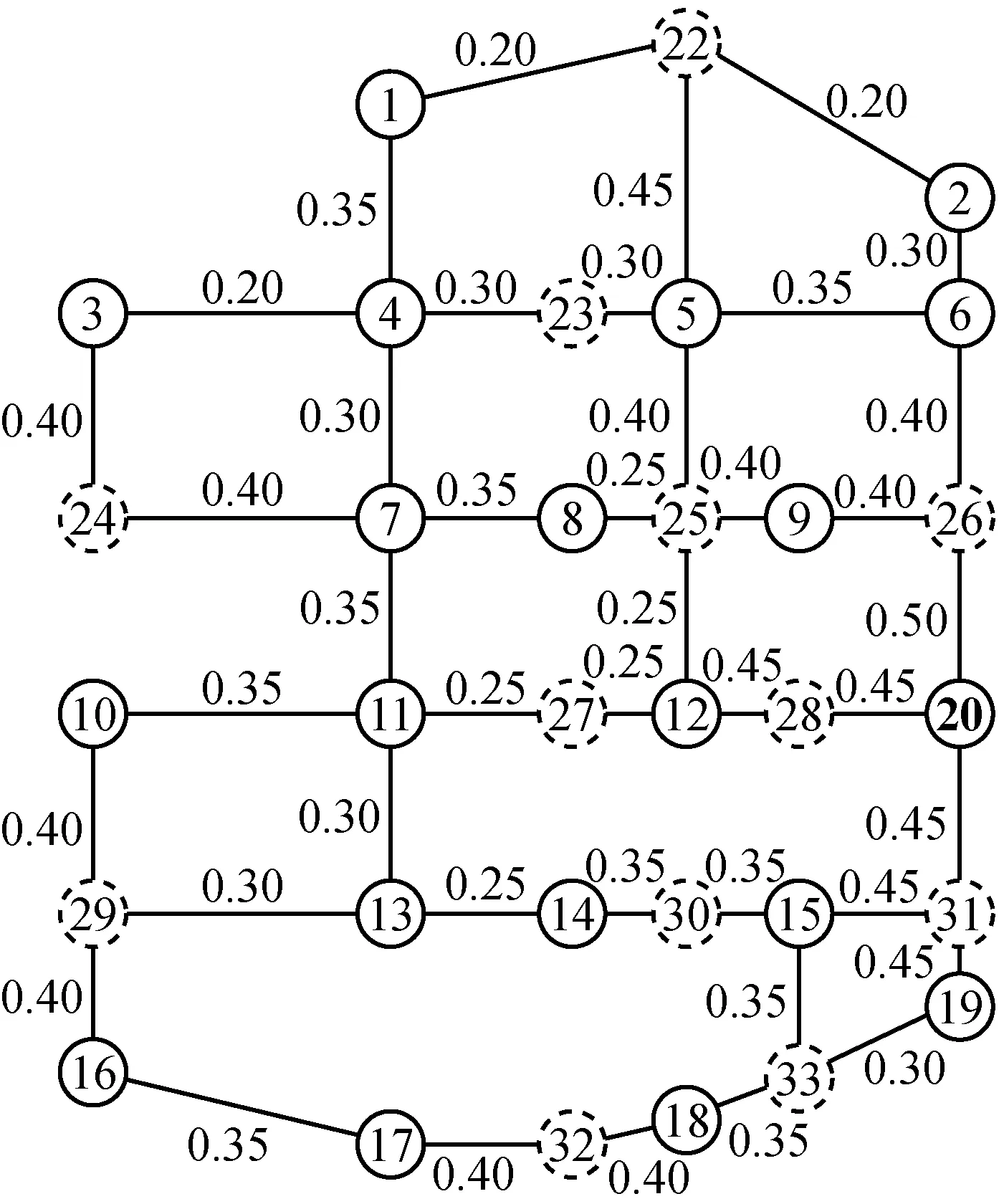
b 基于遗传算法的管网优化方案

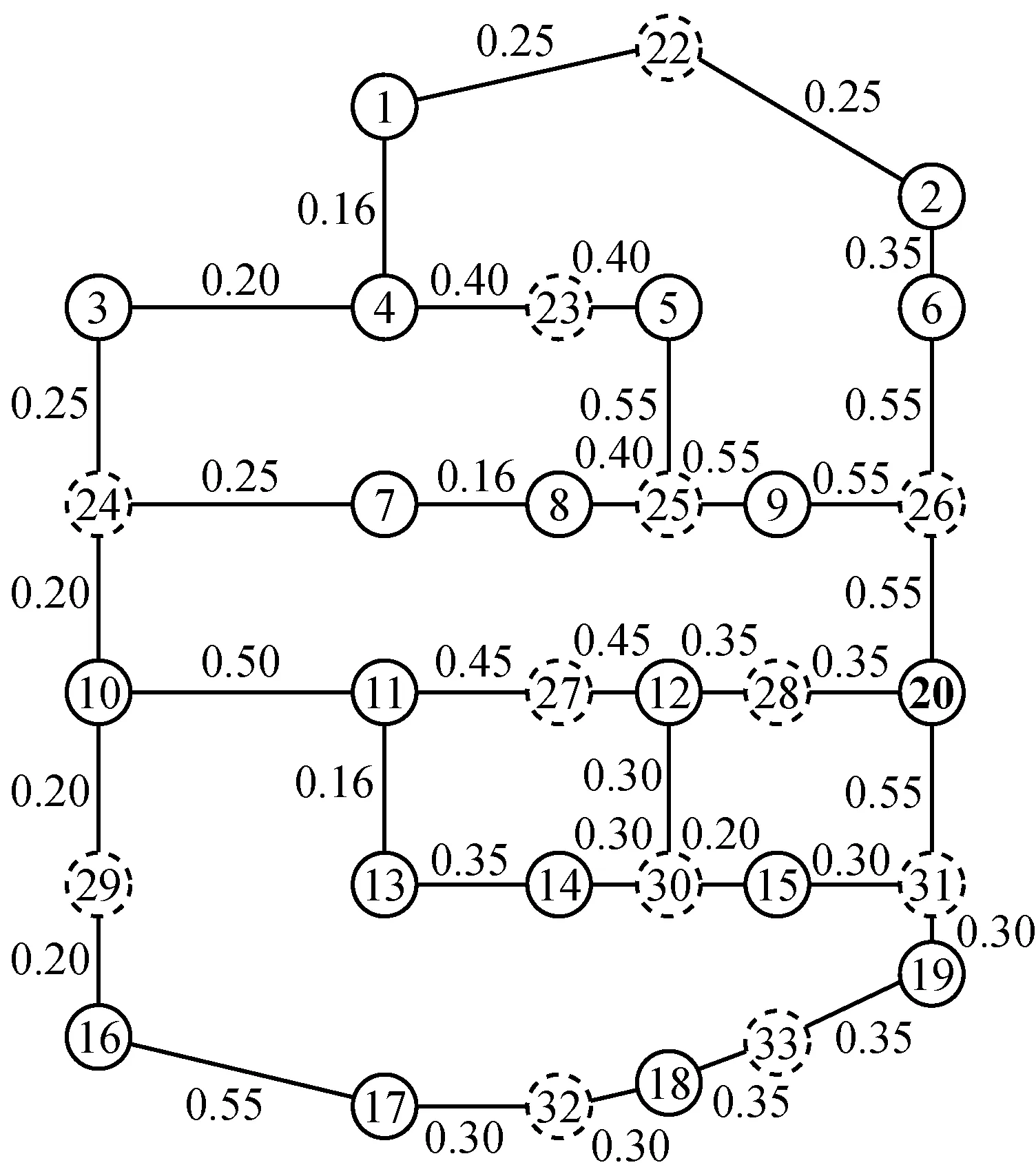
c 基于遗传-模拟退火算法的管网优化方案

图8　管网优化结果

表1　实例1三种优化算法的管网年费用折算值

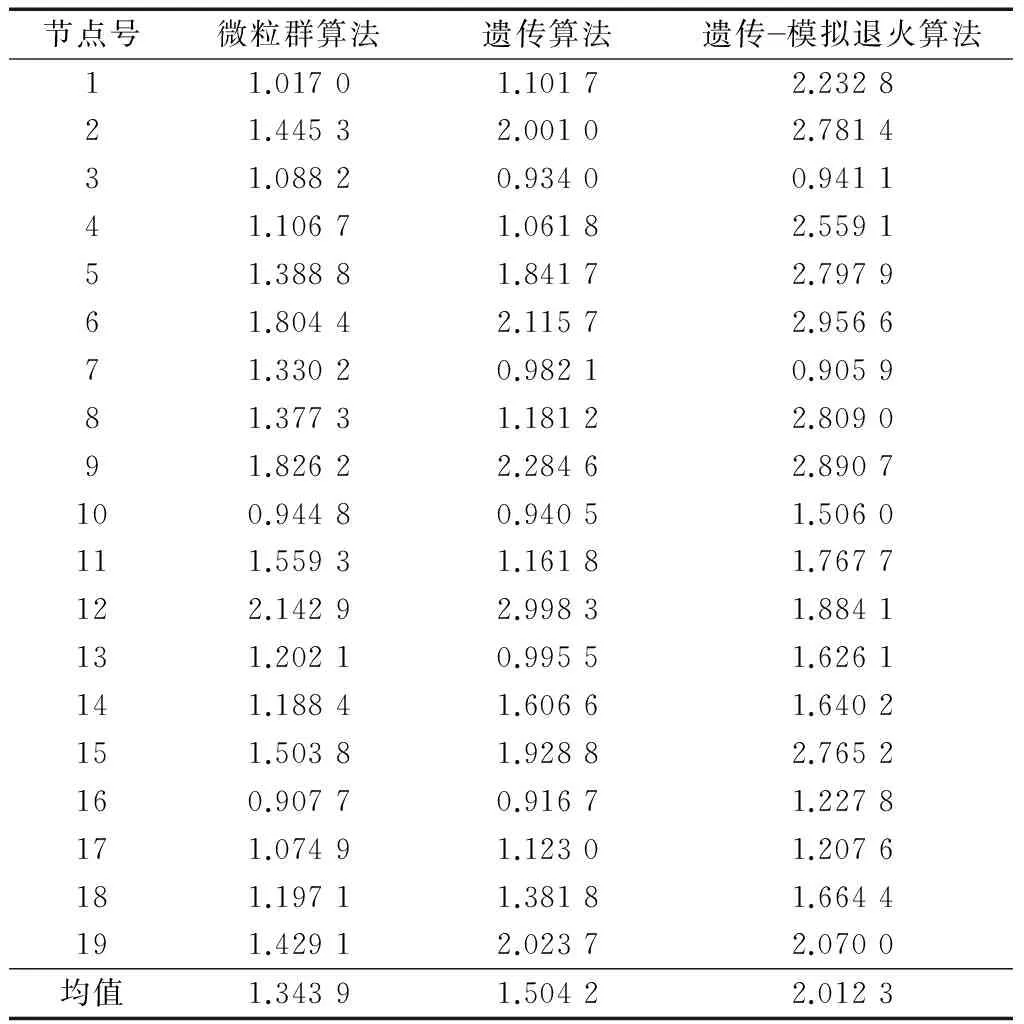
表2　实例1不同优化算法的节点可靠度指标

4.2实例2

图9为绵竹市城区供水管网，这里仅保留了各需水点、水源点和道路信息，其中节点1～58为需水点，59～62为水源点，63～64为道路节点，虚线给出了待建供水管网所在区域的道路分布状况.利用前述3种方法分别对管网重新进行抗震优化设计.考虑到本例中存在与管网由单条管线相连的水源点，因而在管网优化设计中加入判定规则，以使管网中此类管线在优化进程中的环状网判断中不被删除，从而保证所有水源点都与管网相连.考虑地震烈度为8度进行管网抗震优化设计.管材为铸铁.约束条件取最低可靠度指标0.84(对应节点最小可靠度0.8).各算法基本参数选取与实例1同.表3给出3种方法所得优化方案的管网年费用折算值.从表中同样可见，基于自动生成策略的遗传-模拟退火算法具有最好的优化性能，图10为其优化结果.

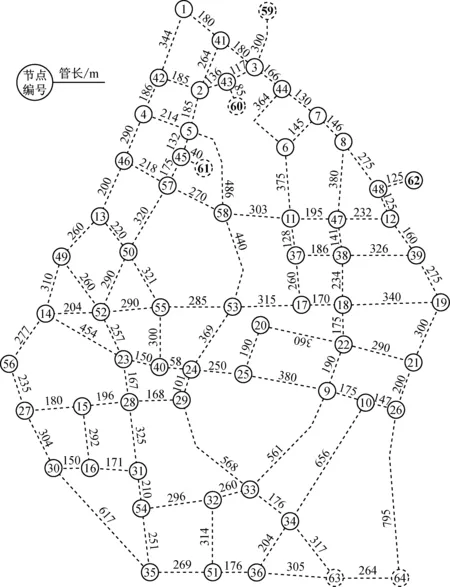
图9　绵竹市待建供水管网

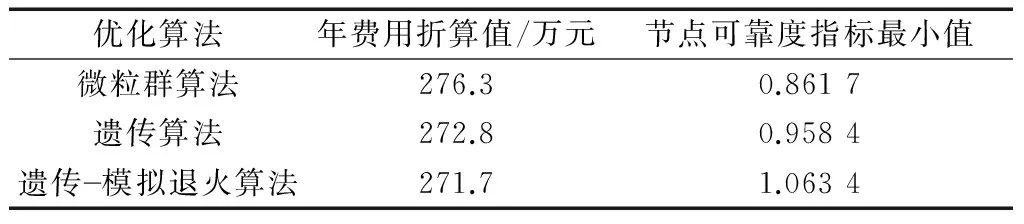
优化算法年费用折算值/万元节点可靠度指标最小值微粒群算法276.30.8617遗传算法272.80.9584遗传模拟退火算法271.71.0634

5结论

结合环形供水管网的判断方法并将道路信息引入管网抗震优化设计中，建立了供水管网的自动生成策略.同时，将自动生成策略嵌入到3种优化算法中，实现遗传算法、遗传-模拟退火混合算法和微粒群算法在供水管网的抗震优化设计中的应用.利用上述3种算法对2个供水管网进行了实例分析，结果表明，遗传-模拟退火算法具有最好的优化能力.

参考文献:

[1]李杰. 生命线工程抗震—基础理论与应用[M]. 北京: 科学出版社， 2005.

LI Jie. Lifeline earthquake engineering—Basic methods and applications [M]. Beijing: Science Press, 2005.

[2]Chen L L, Li J, Xu C C. Seismic reliability-based optimization for water supply network[C]//Proc. the 9th International Conference on Computing in Civil and Building Engineering. Taipei: Taiwan University, 2002:793-798.

[3]李杰，卫书麟，刘威. 基于模拟退火算法的供水管网抗震优化设计[J].地震工程与工程振动，2009，29(3)：108.

LI Jie, WEI Shulin, LIU Wei. Seismic reliability optimization of water distribution networks with simulated annealing algorithms[J]. Earthquake Engineering and Engineering Vibration. 2009, 29(3):108.

[4]邢燕，李杰. 混合优化策略在生命线管网拓扑设计中的应用[J].同济大学学报：自然科学版，2008，36(5)：569.

图10　基于遗传-模拟退火算法的绵竹管网优化方案

XING Yan, LI Jie. Hybrid optimization strategy for topology design of lifeline networks[J]. Journal of Tongji University: Natural Science, 2008，36(5)：569.

[5]徐良，刘威，李杰. 基于微粒群算法的供水管网抗震优化设计[J].防灾减灾工程学报，2010，30(3)：269.

XU Liang, LIU Wei, LI Jie. Seismic reliability optimization of water distribution network with particle swarm algorithm[J]. Journal of Disaster Prevention and Mitigation Engineering, 2010，30(3)：269.

[6]李杰，邢燕. 基于可靠度的生命线工程网络抗震设计[J]. 同济大学学报：自然科学版，2010，38(6)：783.

LI Jie, XING Yan. Reliability-based seismic design of lifeline networks[J]. Journal of Tongji University: Natural Science, 2010，38(6)：783.

[7]陈玲俐，李杰. 城市供水管网系统抗震功能可靠度分析[J]. 工程力学，2004，21(4)：45.

CHEN Lingli, LI Jie. Aseismatic serviceability analysis of water supply network[J]. Engineering Mechanics，2004，21(4)：45.

[8]严煦世, 刘遂庆. 给水排水管网系统[M]. 北京: 中国建筑工业出版社, 2003.

YAN Xushi, LIU Suiqing. Water and wastewater pipeline network systems[M]. Beijing: China Architecture and Building Press, 2003.

[9]邵知宇. 给水管网分段线性优化模型[D]. 上海: 同济大学，2001.

SHAO Zhiyu. Piecewise linear optimization model of water pipeline network[D]. Shanghai: Tongji University, 2001.

[10]Dijkstra E W. A note on two problems in connexion with graphs[J]. Numerische Mathematlk, 1959，1(1):269.

[11]Holland J H. Adaptation in natural and artificial systems[M]. ANN Arbor: University of Michigan Press, 1975.

[12]Kirkpatrick S, Gelatt C D, Vecchi M P. Optimization by simulated annealing[J]. Science, 1983, 220(4958):671.

[13]Jeong I, Lee J. Adaptive simulated annealing genetic algorithm for system identifictation [J]. Engineering Applications of Artificial Intelligence, 1996, 9(5):523.

[14]Kennedy J. A new optimizer using particle swarm theory [C]//The Sixth International Symposium on Micro Machine and Human Science. Nagoya: Nagoya Municipal Industrial Research Institute, 1995: 39-43.

收稿日期：2015-07-07

基金项目：国家自然科学基金面上项目(51278380)

中图分类号：P315.9

文献标志码：A

Seismic Topology Optimization Algorithms for Water Distribution Networks based on Automatic Generation Strategy

LIU Wei1,2， YUAN Hongwei3, XU Liang4

(1. State Key Laboratory for Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China; 2. College of Civil Engineering, Tongji University, Shanghai 200092, China; 3. Beijing Institute of Architectural Design, Beijing 100045, China; 4.Shanghai Nuclear Engineering Research & Design Institute, Shanghai 200233, China)

Abstract：Taking water distribution network’s annual reduced cost as optimization object and seismic reliability as optimization restriction, a network topology optimization model is established. Then, an automatic generation strategy based on the existed road information is proposed. Combining with ring network generation method and automatic generation strategy, three approaches, a genetic algorithm, a simulated annealing genetic algorithm and a particle swarm algorithm, are employed to solve the seismic optimization model. Two networks are optimized using three algorithms and a comparative study is performed. The comparison indicates that the simulated annealing genetic algorithm performs the best.

Key words：water distribution network; automatic generation strategy; genetic algorithm; simulated annealing genetic algorithm; particle swarm algorithm

第一作者： 刘威(1976—)，男，副教授，工学博士，主要研究方向为生命线工程防灾.E-mail：liuw@tongji.edu.cn