基于Mehler公式的等效相关系数求解技术

范文亮, 杨朋超, 李正良1,

(1. 重庆大学 山地城镇建设与新技术教育部重点实验室， 重庆 400045; 2. 重庆大学 土木工程学院， 重庆 400045;3. 加州大学欧文分校 土木与环境工程系，欧文 92697)



基于Mehler公式的等效相关系数求解技术

范文亮1,2,3, 杨朋超2, 李正良1,2

(1. 重庆大学 山地城镇建设与新技术教育部重点实验室， 重庆 400045; 2. 重庆大学 土木工程学院， 重庆 400045;3. 加州大学欧文分校 土木与环境工程系，欧文 92697)

摘要：首先基于等效相关系数的传统二维积分方程，引入二维相关标准正态密度函数的Mehler级数展开公式，然后导出了等效相关系数的无穷次代数方程及其收敛特性，实现了积分方程向代数方程的转变，进一步完善了Nataf变换理论.同时，通过方程截断近似的方式给出了求解等效相关系数的迭代方法.由于避免了二维相关标准正态密度函数的积分和利用了代数方程系数的可重复性及一维积分特性，本文方法具有广泛的适用范围，且兼顾了计算的精度和效率.最后，通过算例验证了方法的有效性和精确性.

关键词：等效相关系数； 相关随机向量； Nataf变换； Mehler公式； 代数方程

在结构随机分析及可靠度分析中，几何参数、材料特性参数及外部荷载等通常为随机变量.不同类别随机变量可视为相互独立，但同类别随机变量往往存在相关性.当各变量均为正态变量时，只需通过简单的线性变换即可将其转换为独立的正态变量[1].对于相关非正态变量，若已知联合概率密度函数，则可利用Rosenblatt变换实现原变量向独立标准正态变量的转换[2-5]；若仅已知边缘概率密度函数和相关系数矩阵，Nataf变换则不失为一种行之有效的方法[6-9].然而，获得变量的联合概率密度函数往往比较困难，而确定边缘概率密度函数和相关系数则相对较为容易，因此Nataf变换更具有实用价值.

Nataf变换主要涉及2个步骤：相关非正态变量转换为相关正态变量和相关正态变量转换为独立正态变量.前者主要是相关正态变量的等效相关系数的计算，亦是目前Nataf变换研究的主要内容.

等效相关系数的求解主要有解析法、半解析法、数值解法和数值模拟法等.解析法可以直接给出等效相关系数的精确计算公式，准确、高效，但仅适用于特定的变量，如均匀分布变量[10]和对数正态变量[11].半解析法则是给出等效相关系数的近似表达式[6,12].与解析法类似，半解析法在享有高效性这一优点的同时亦具有适用范围有限的缺点，且精度有所下降.数值解法是将二维数值积分和非线性方程求根结合起来获得等效相关系数近似解的方法.根据积分变量所在空间的不同，又可分为相关标准空间的数值解法[13-14]和独立标准正态空间的数值解法[7,15].相关标准正态空间中，由于联合标准正态密度函数在相关系数接近于±1时为集中于45°或135°的剧烈变化函数，导致常规二维数值积分出现困难，从而得到不正确的等效相关系数的解；独立标准正态空间的二维积分方程则是由相关标准正态空间的二维积分方程辅以相关结构分解得到的，但是相关结构分解的变量顺序依赖性导致了独立标准正态空间方程的不唯一性.数值模拟方法可以实现多个二维积分方程的同时求解[16-17].然而，由于涉及多个相关正态变量的相关结构分解，当等效相关系数矩阵非正定时将不能给出合适的数值解；此外，该方法的效率并不一定优于数值方法.由于不受变量类型和分布参数的限制，且执行较为方便，数值方法得到了广泛的应用.

除求解积分方程外，尚有通过更易求解的代数方程计算等效相关系数的数值方法.文献[15]根据Weierstrass 近似理论，对于独立标准正态空间的二维积分方程导出了关于等效相关系数的近似代数方程，但仍涉及二维数值积分的计算.事实上，若对两相关变量各自的等概率变换关于Hermite多项式进行正交展开，可以导出一无穷次的代数方程[18-20]，其中仅包含一维数值积分.对于二阶矩随机变量，该展开式收敛，可通过截断的代数方程获得等效相关系数的近似解.尽管该方法亦是求解等效相关系数的方法，但是其建立方程的思路与传统的Nataf变换截然不同，且只存在代数方程形式，更常见于随机过程的混沌多项式展开研究中，文献[20]亦将其与Nataf变换区分开.

为此，本文在传统的Nataf变换的框架内，结合Mehler公式[21]，直接基于相关标准正态空间的二维积分方程，导出了等效相关系数的无穷次代数方程及其收敛特性，并发展了求解等效相关系数近似解的高效迭代法.

1Nataf变换及等效相关系数

1.1Nataf变换

1.1.1等效相关系数方程

定义n维相关随机向量

(1)

式中：FI(·)为Θi(i=1,…,n)的累积分布函数；n为随机变量的数量.ρ为相关系数矩阵，ρ=[ρij]n×n.若引入等概率变换，有

(2)

式中：Xi为Θi对应的标准正态变量；Φ-1(·)为标准正态累积分布函数Φ(·)的反函数.于是，Θi与Θj的相关系数ρij和Xi与Xj的等效相关系数ρij*满足如下方程：

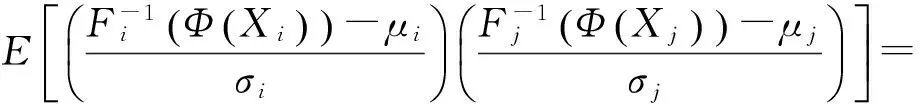
(3)

式中：E[·] 表示期望运算；μi，σi分别为Θi的均值和标准差；Fi-1(·)为Fi(·)的反函数；φ2(·)为二维相关标准正态变量的联合概率密度函数，即

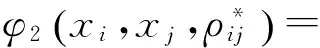
(4)

求解式(3)即可得到ρij*，进而确定等效相关系数矩阵ρ*=[ρij*]n×n.

1.1.2相关结构分解

经由线性变换，可将相关矩阵为ρ*的标准正态向量X=(X1,…,Xn)T转化为独立的标准正态向量U=(U1,…,Un)T.先对ρ*进行Cholesky分解

(5)

式中：C为下三角矩阵.然后，有

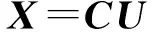
(6)

特别地，当n=2时式(6)可简化为

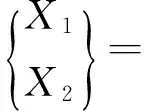
(7)

显然，X1，X2和U1，U2的关系与变量的排序有关.对于多变量情形，亦存在相似的结论.

1.1.3Nataf变换

综合式(2)与式(6)即可形成Nataf变换

(8)

不难发现，相对于其他步骤，方程式(3)为二维积分方程，其求解过程较为复杂，是Nataf变换的关键.且当有n个相关变量时，则存在n(n-1)/2个二维积分方程.

1.2等效相关系数的求解

1.2.1相关标准正态空间

式(3)的积分变量Xi与Xj为相关的标准正态变量，因此式(3)可视为相关标准正态空间中关于等效相关系数的二维积分方程.对其引入二维数值积分可有

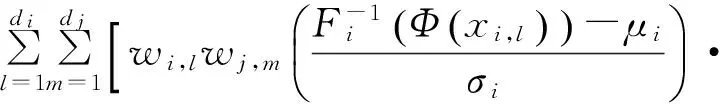
(9)

式中：xi,l，wi,l和xj,m，wj,m分别为Xi和Xj的第l个和第m个求积节点和权系数；di和dj分别为Xi和Xj所采用的节点数.

当ρij*接近±1时，比如ρij*=0.99，若采用di=dj=11的等间距数值求积公式，求积节点的位置以及φ2(·)的图形如图1所示.不难发现，绝大部分节点对应的函数值接近零，为无效节点.因此，基于式(9)计算在ρij*接近±1时的等效相关系数是不高效的，甚至可能是不准确的.

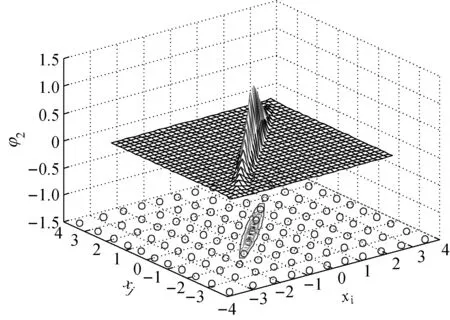
图1　二维相关标准正态联合概率密度函数及积分节点

1.2.2独立标准正态空间

事实上，将式(3)和式(7)结合起来，可将Xi与Xj转换为独立的Ui与Uj，从而得到独立标准正态空间的二维积分方程，即

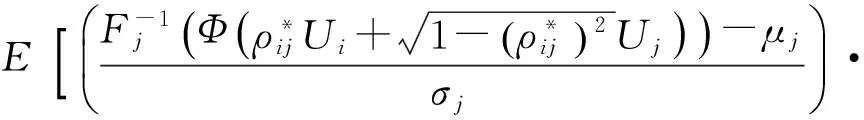
φ(ui)φ(uj)duiduj

(10)

显然，独立标准正态空间的二维积分方程克服了相关标准正态空间的二维积分方程在ρij*接近±1时难以求解的困难.

值得指出的是，文献[7]计算等效相关系数的过程与求解方程式(10)在本质上是等价的，但是并未给出显式的表达，而是将其分解为二维积分方程和相关结构分解两部分，文献[16]则将可显式化的二维相关结构分解与二维积分方程结合起来，给出了与式(10)等价的显式表达式.

若对调Xi与Xj在相关结构分解时的顺序，亦可得一个关于等效相关系数的二维积分方程，即

(11)

式(10)与式(11)均是关于ρij*的二维积分方程，但是两者的解往往并不相同，与传统的Nataf变换中等效相关系数解的唯一性认知不符.

1.2.3Weierstrass近似

无论是式(10)和式(11)均是二维积分方程，求解并不方便.为此，可引入Weierstrass 近似理论将其近似为代数方程，即

(12)

式中:bk为系数；m0为方程的最高次数.文献[15]中建议m0=8.

显然，式(12)的求解较式(10)或式(11)更简单，但该方法克服不了独立标准正态空间的解不唯一这一缺陷；此外，bk的计算仍涉及二维数值积分.

1.2.4无穷次代数方程

与传统Nataf变换理论不同，若基于任意二阶矩变量的混沌多项式展开，亦可给出ρij与ρij*的关系式.对式(2)的逆变换进行混沌多项式展开得

(13)

式中

(14)

Hk(·)为概率Hermite正交多项式，即

(15)

于是，根据Hermite多项式的正交特性可有

(16)

对其截断即可得到ρij*应满足的代数方程为

(17)

文献[21]中建议m0=10.

与式(12)相比，式(16)具有唯一性，且系数仅涉及一维数值积分.然而，与经典的Nataf变换理论相比，其建立的方式截然不同；就方程的形式而言，式(16)形式单一，而Nataf变换的方程形式多样.事实上，若引入Mehler公式，由式(3)亦可导出无穷次的代数方程.

2等效相关系数求解的新方法

2.1Mehler公式

式(4)既可视为xi和xj的函数，亦可视为ρij*的函数，故可对其关于ρij*进行Taylor级数展开.

1866年，Mehler给出了以Hermite多项式为基的式(4)的级数展开表达式，即

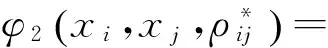
Hk(xi)Hk(xj)

(18)

且此展开式在|ρij*|<1时收敛.

2.2无穷次的等价代数方程

将式(18)代入式(3)并化简可得

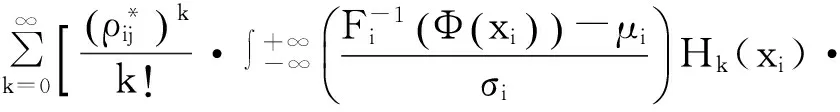
φ(xi)dxi·

(19)

若记

(20)

则式(19)可简写为

(21)

根据Hermite多项式的正交性质有

(22)

显然，式(21)可改写为

(23)

且必有

(24)

与文献[6]的定理2相符.

显然，式(23)亦是关于ρij*的无穷次代数方程，且当|ρij*|<1时该级数展开式方程收敛.此外，该级数展开方程亦具有唯一性.

与式(3)、式(10)和式(11)相比，式(23)是更为熟悉、更易求解的代数方程，且其中仅涉及到一维积分，亦不存在适用范围限制.尤其值得指出的是，Ii,k在求解ρi,j1*和ρi,j2*时均可以利用，因此计算系数所需要的工作量近似与变量的数量n成正比，具有很高的计算效率.

与式(12)相比，式(23)具有唯一性，且仅涉及一维积分.

与式(16)相比，式(23)是从经典的Nataf变换的二维积分方程出发导出的结果，是积分方程式(3)的代数方程形式，是对Nataf变换理论的完善和有效补充.由于是针对特定函数的级数展开，其收敛特性很容易确定，而与Θi和Θj的分布类型无关.此外，就系数的计算而言，式(20)中被积函数的非线性程度相对较易判定，即为Rosenblatt变换的非线性程度与k阶Hermite多项式的非线性程度之和，因此，更容易确定一维数值积分方案.

2.3数值解法

由于级数展开的收敛性，可截取部分项构建近似方程，即

(25)

为求解该方程，可分为3个步骤：①确定系数Ii,k；②确定合适的m0值；③求解非线性代数方程.

2.3.1Ii,k的计算

由于式(20)是以标准正态密度函数为权的积分，因此可以方便地引入Gauss-Hermite积分公式获得其数值解，即

(26)

式中：xGH,l和wGH,l分别是Gauss-Hermite求积公式的节点和权系数.通常，各变量转化为标准正态变量时取5～7次足够，且式(25)中m0一般小于10，因此在式(26)中取di=9～11是较为合适的.

2.3.2合适的m0

为确定合适的m0，可采用迭代法.过程如下：

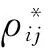
(2) 令q=q+1，mq=mq-1+2，计算新增加的Ii,k和Ij,k(k=mq-1+1,mq)，同时计算式(25)右端新增项的值及其总和Sq.

(3) 如果|(Sq-Sq-1)/Sq|<ε(ε为一很小的数值，文中取为10-4)，则m0=mq-1；否则，返回步骤(2)进行迭代.

显然，通过此迭代过程自适应地确定m0值较经验性地确定m0值更具科学性，且往往可以避免许多不必要的系数的计算，具有更高的精度和效率.

2.3.3非线性代数方程的求解

确定m0值后可以直接采用各类成熟的非线性方程的解法求解非线性代数方程式(25).

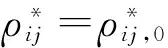
(27)

3特殊情形的验证

对于某些特殊情形，根据式(23)可以得到一些有意义的结果.

3.11个正态变量

对于Θi与Θj存在一个正态变量的情形，不妨令Θi为正态变量.根据正态变量的性质，显然有

(28)

将上式代入式(20)，并利用Hermite多项式的正交性可有

(29)

将式(29)代入式(23)可得

(30)

与文献[6]的定理4吻合.因此，式(30)可方便且精确地计算正态变量与其他变量的等效相关系数.

3.22个正态变量

若Θj亦为正态变量，易知

(31)

与线性变换不改变Pearson相关系数的常识相符，亦与文献[6]的定理5吻合.

3.3正态变量和对数正态变量

若Θj为对数正态变量，即lnΘj～N(μln Θj,σln Θj)则有

(32)

于是

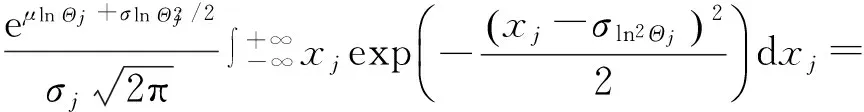
(33)

将其代入式(30)可得

(34)

式中：δj为Θj的变异系数.不难发现，式(34)与文献[6]的解析解相吻合.

4算例分析

为了验证本文方法的正确性和适用性，文中对3类随机向量情形进行了较为详细的分析.

4.1均匀分布随机向量

若Θ1与Θ2均服从[0,1]均匀分布，其相关系数为ρΘ，那么对应的正态变量X1与X2的相关系数ρX与ρΘ存在如下解析关系[10]:

(35)

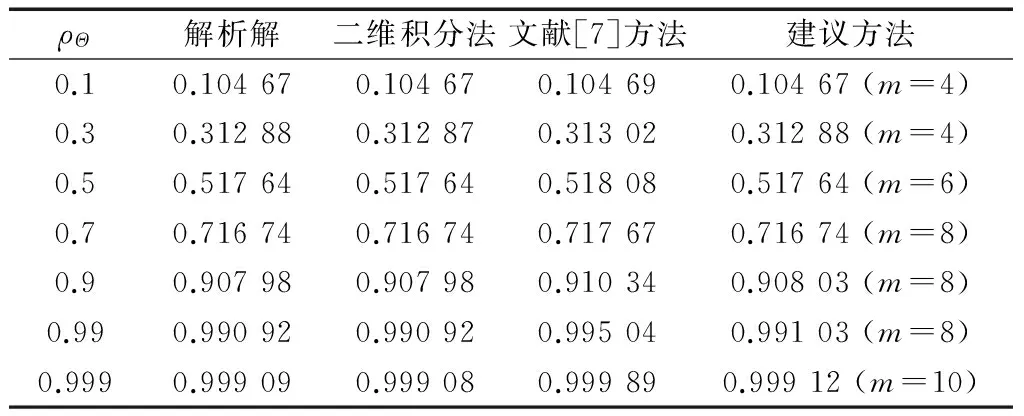
表1　均匀分布的等效相关系数

当ρΘ取不同值时，表1给出了分别由直接二维积分法(即直接求解方程(9))、文献[7]方法(即求解方程(10))和建议方法得到的ρX的数值解，同时亦给出了由式(35)确定的解析解.经对比，不难发现，二维积分法、建议方法均具有很高的精度，而文献[7]方法计算精度最低.对于原变量服从均匀分布的情形，当相关系数较小时，式(23)收敛很快，只需几项就可以达到非常高的精度；随着相关系数增大，收敛趋缓，但即使对于ρΘ接近于1的情形，取m=10亦足够.

4.2对数正态随机向量

当Θ1及Θ2均服从对数正态分布时，ρX与ρΘ的解析关系如下[11]：

(36)

由于ρX和ρΘ的关系仅与σln Θ1，σln Θ2有关，而与μln Θ1，μln Θ2无关，因此可令lnΘ1～N(0,σln Θ1)，lnΘ2～N(0,σln Θ2).

图2给出了σln Θ1，σln Θ2的不同组合工况下分别取m为4，6时式(25)与式(36)的逼近程度.不难发现，对于对数正态变量，取m=4基本可以得到较为理想的精度.此外，表2是各工况的变量概率分布，表3给出了表2不同工况时3类方法数值解与解析解的对比.结果表明，建议方法具有非常理想的精度；二维积分法、文献[7]方法对ρΘ接近于1的情形计算结果误差较大，如工况6及工况7.

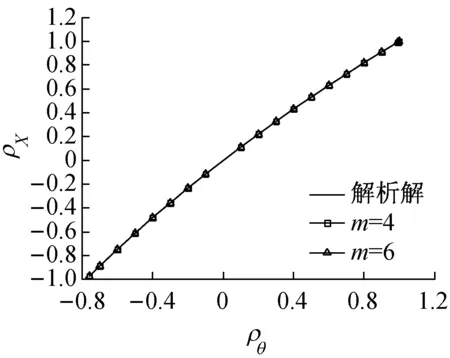
a σln Θ1=σln Θ2=0.5

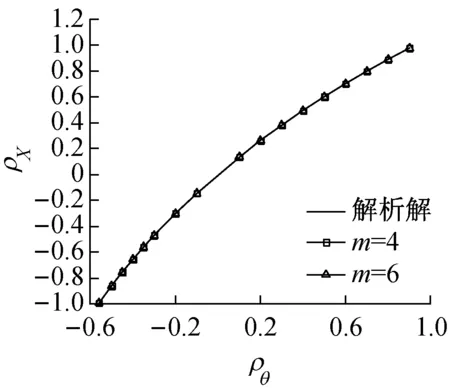
b σln Θ1=0.5, σln Θ2=1.0

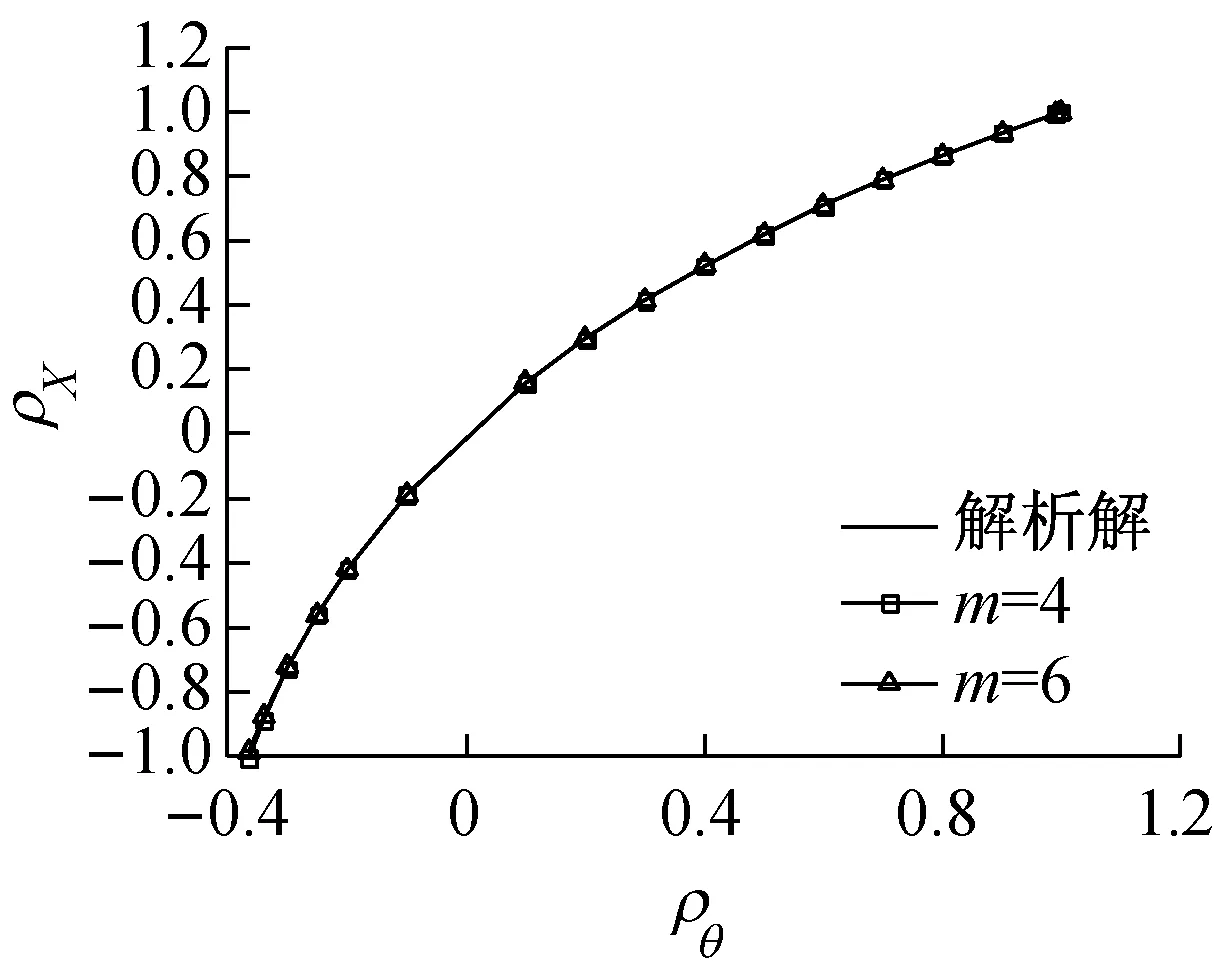
c σln Θ1=σln Θ2=1.0

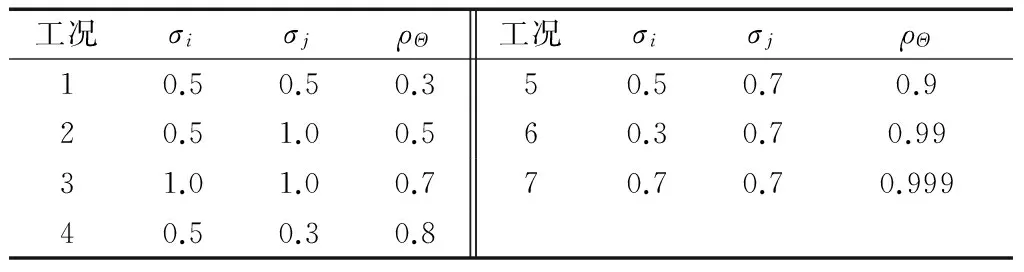
表2　各工况及变量概率分布信息

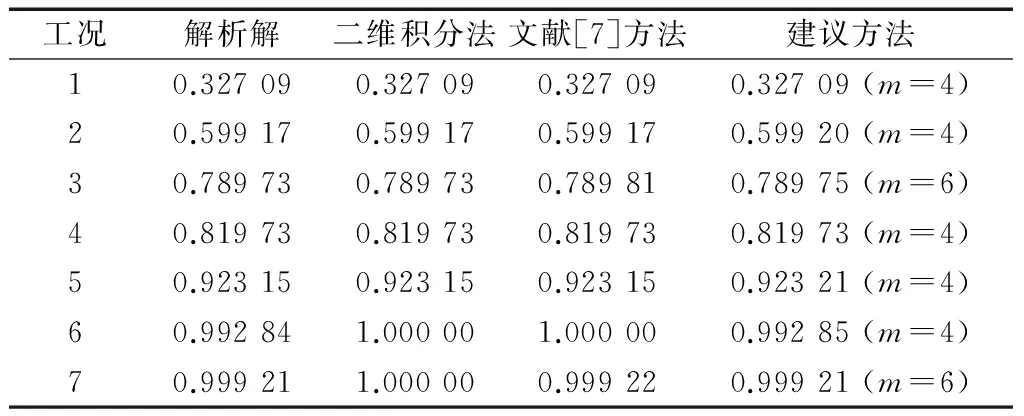
表3　对数分布的等效相关系数

4.3任意分布相关随机向量

假定随机变量Θ1与Θ2具有相同的均值μΘ=1.0及变异系数δΘ=0.2.依据随机变量Θ1与Θ2的分布类型不同，考虑表4所示3种工况.当ρΘ取不同值时，采用直接二维积分法、文献[7]方法和建议算法给出ρX的数值解，计算结果如表5.显然，对于此3种工况，建议方法与二维积分法、文献[7]方法的计算结果具有高度的一致性，说明建议方法对任意分布相关随机变量等效相关系数求解问题适用.

表4　各工况及变量分布类型

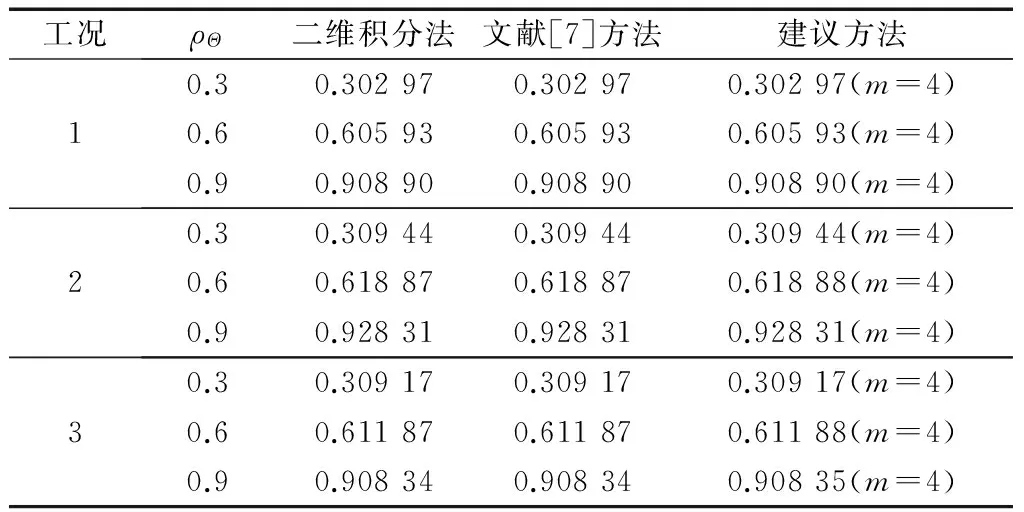
表5　不同工况ρX计算结果

此外，由于建议方法仅涉及一维数值积分和代数方程的求解，更易于实现.

5结论

等效相关系数的求解是Nataf的关键环节，本文基于Mehler公式导出了关于等效相关系数的无穷次代数方程，完善了Nataf变换理论的框架；同时，基于该无穷次代数方程的收敛特性给出了由截断方程逐步逼近的迭代求解思路，兼顾了方程求解的精度和效率.由于既不涉及关于联合标准正态密度函数的积分，又只包含一维积分，且该一维积分仅取决于变量自身，因此建议方法具有广泛的适用范围、理想的计算精度和很高的计算效率，对于相关变量较多的情形尤其如此.

参考文献:

[1]李杰. 随机结构系统——分析与建模[M]. 北京：科学出版社, 1996.

LI Jie. Stochastic structural system: Analyzing and modeling [M]. Beijing: Science Press, 1996.

[2]Rosenblatt M. Remarks on a multivariate transformation [J].The Annals of Mathematical Statistics, 1952, 23(3): 470.

[3]Zhao Y G, Ono T. New point-estimates for probability moments [J]. Journal of Engineering Mechanics, 2000, 126(4): 433.

[4]Huang X, Zhang Y. Reliability-sensitivity analysis using dimension reduction methods and saddlepoint approximations [J]. International Journal for Numerical Methods in Engineering, 2013, 93(8): 857.

[5]Honenbichler M, Rackwitz R. Non-normal dependent vectors in structural safety [J]. Journal of the Engineering Mechanics Division ASCE, 1981, 107(6): 1227.

[6]Liu P L, Der Kiureghian A. Multivariate distribution models with prescribed marginals and covariances [J]. Probabilistic Engineering Mechanics, 1986, 1(2): 105.

[7]Li H S, Lv Z Z, Yuan X K. Nataf transformation based points estimate method [J]. Chinese Science Bulletin, 2008, 53(17): 2586.

[8]Der Kiureghian A, Liu P L. Structural reliability under incomplete probability information [J]. Journal of engineering mechanics, 1986, 112(1): 85.

[9]吕大刚. 基于线性化Nataf变换的一次可靠度方法[J]. 工程力学, 2007, 24(5): 79.

LV Dagang. First order reliability method based on linearity Nataf transformation [J]. Engineering Mechanics, 2007, 24(5): 79.

[10]Li S T, Hammond J L. Generation of pseudo random numbers with specified univariate distributions and correlation coefficients [J]. IEEE Transactions on Systems, Man and Cybernetics, 1975, SMC-5(5): 557.

[11]Mostafa M, Mahmoud M. On the problem of estimation for the bivariate lognormal distribution [J]. Biometrika, 1964, 51(3/4): 522.

[12]姚继涛, 董振平. 随机变量的相关性和结构可靠度[J]. 西安建筑大学学报, 2000, 32(2): 114.

YAO Jitao, DONG Zhenping. Correlativity of random variables and structural reliability [J]. Journal of Xi’an University of Architecture & Technology, 2000, 32(2): 114.

[13]Cario M C, Nelson B L. Modeling and generating random vectors with arbitrary marginal distributions and correlation matrix [R]. Evanston: Northwestern University, 1997.

[14]Kugiumtzis D, Bora-Senta E. Normal correlation coefficient of non-normal variables using piece-wise linear approximation [J]. Computational Statistics, 2010, 25(4): 645.

[15]Xiao Q. Evaluating correlation coefficient for Nataf transformation [J]. Probabilistic Engineering Mechanics, 2014, 37: 1.

[16]Chen H F. Initialization for NORTA: Generation of random vectors with specified marginal and correlations [J]. Informs Journal on Computing, 2001, 13(4): 312.

[17]Niavarani M R, Smith A J R. Modeling and generating multi-variate-attribute random vectors using a new simulation method combined with NORTA Algorithm [J]. Journal of Uncertain Systems, 2013, 7(2): 83.

[18]Sakamoto S, Ghanem R. Polynomial chaos decomposition for the simulation of non-Gaussian non-stationary stochastic processes [J]. Journal of Engineering Mechanics ASCE, 2002, 128(2): 190.

[19]Phoon K K, Nadim F. Modeling non-gaussian random vectors for FORM: State-of-the-art review [C]// International Workshop on Risk Assessment in Site Characterization and Geotechnical Design. Bangalore: Indian Institute of Science, 2004: 55-85.

[20]张坤, 吴帅兵, 李典庆. 基于Hermite多项式的等效相关系数求解及可靠度分析[J]. 武汉大学学报:工学版, 2012, 45(2): 200.

ZHANG Kun, WU Shuaibing， LI Dianqing. Solution of equivalent correlation coefficient and reliability analysis using Hermite polynomials [J]. Engineering Journal of Wuhan University, 2012, 45(2): 200.

[21]Kibble W F. An extension of a theorem of Mehler’s on Hermite polynomials [J]. Mathematical Proceedings of the Cambridge Philosophical Society, 1945, 41(1): 12.

收稿日期：2015-07-21

基金项目：中央高校基本科研业务费(CDJZR 12200015, CDJZR 12200059)；国家自然科学基金(50908243)

中图分类号：TU311;TB114

文献标志码：A

A Technique for Solution of Equivalent Correlation Coefficients Based on the Mehler’s Formula

FAN Wenliang1,2,3, YANG Pengchao2, LI Zhengliang1,2

(1. Key Laboratory of New Technology for Construction of Cities in Mountain Area Ministry of Education, Chongqing University, Chongqing 400045, China; 2. School of Civil Engineering, Chongqing University, Chongqing 400045, China; 3. Department of Civil and Environmental Engineering, University of California-Irvine, Irvine 92697, USA)

Abstract：Firstly, the Mehler’s formula, an equivalent series expansion of the bivariate normal probability density function (PDF), is introduced into the original equation with respect to the equivalent correlation coefficients, which is defined in the two dimensional dependent normal space. Then the equivalent algebraic equation with infinite terms is deduced straightforwardly, together with its convergence property. Theoretically, this work can be treated as the improvement of the Nataf transformation. Meanwhile, an iterative method for approximate solutions of equivalent correlation coefficients is proposed based on the truncated algebraic equation. Without the integral of bivariate normal PDF and with the merits of the reusability of coefficients of algebraic equations, the proposed method is of wide applicability, high efficiency and high precision. Lastly, the accuracy and rationality of this method are verified by examples.

Key words：equivalent correlation coefficients; dependent random vector; Nataf transformation; Mehler’s formula; algebraic equation

第一作者： 范文亮(1979—)，男，副教授，工学博士，主要研究方向为结构工程、随机系统分析和可靠度分析. E-mail:davidfwl@126.com