基于BP人工神经网络的离散型车间生产调度指标预测模型的研究
2016-02-26谈宏志金礼伟杨家荣许伟吕伟
谈宏志 金礼伟 杨家荣 许伟 吕伟

【摘 要】离散型车间的生产调度对车间生产有至关重要的影响,该研究中车间调度指标用工时达成率来表示。加工工时、批次大小、加工设备数量、原材料到位情况、工人、设备的健康状况对工时达成率都有不同程度的影响,使得工时达成率有很大的不确定性。如果能够准确控制工时达成率的大小,生产决策者们就可以通过调整设备、批次大小、原材料的采购周期使得车间输出最大生产力。本文通过人工神经网络建立工时达成率预测模型,实现对车间工时达成率的预测,并探讨两种算法,寻找能够在降低训练时间的前提下提高神经网络模型准确性的算法,其中模拟退火算法(Simulated Annealing ,SA)是首次以搜索初始值周围点获得最佳点的形式被应用,马克夸特(Levenberg-Marquardt)算法用来在特殊点中寻求局部最优,最后对比模拟退火算法和马克夸特混合算法及马克夸特算法,并通过调整神经网络的数量得到最佳的预测模型。
【关键词】BP人工神经网络;车间调度;模拟退火算法;SA\LM混合算法
0 引言
车间调度指标工时达成率是评价车间调度优异程度的重要指标,它直接体现出车间设备的利用率、工人效率、库存大小,同时工时达成率的影响因素很多,如原料到位情况、设备健康状况、人员到岗状况、批次大小、加班情景等。车间调度问题是满足任务条件和约束要求的资源分配问题,是最困难的组合优化问题,解决车调度问题首先要建立准确的车间生产模型,模型的优异程度由预测输出指标的准确性决定,BP人工神经网络是建立预测模型寻求最优值的有效工具。
国内外学者对人工神经网络在调度问题及建立预测模型有相关研究。A.Azadeh、M.Jeihoonian等采用集成神经网络研究了双标准双级装配流水作业调度问题[1];Azadeh提出了采用复杂人工神经网络和模糊优化算法优化仿真模型来解决流水生产车间的调度问题[2];Golmohammadi, Davood等人采用神经网络模型开发的智能系统,研究表明零部件的批次大小比原材料的到位时间及延时时间对调度结果更有影响[3];A.Azadeh, A. Negahban采用混合人工神经网络仿真并优化随机生产的调度问题[4];Braglia 和 Grassi提出了最小化车间平均工时并最大限度延迟的车间调度混合模型,他们采用Nawaz–Enscore–Ham和多目标遗传局部搜索算法来解决问题[5];祝翠玲、蒋志方等基于BP神经网络建立空气质量预测模型,将空气污染源的数据输入到该模型中,可以准确预测出污染物的检测值[6];陈廉清,郭建亮等提出了基于BP神经网络和遗传算法构建表面粗糙度预测模型的开放式试验系统,该系统提高了外圆磨削产品表面粗糙度预测模型的收敛速度和预测精度[7];崔吉峰、乞建勋等提出了采用粒子群算法改进BP神经网络算法,建立了对能源需求的预测模型,作者首先利用灰色预测方法和自回归移动平均模型建立初步预测结果,再将该结果作为BP神经网络的输入,在此基础上进行训练和预测,将预测精度提高了5%左右[8];张喜忠作了基于神经网络预测模型的发动机异响信号提取的研究,丰富了发动机异响信号提取的新方法,拓宽了发动机故障诊断的应用范围[9];王德明、王莉提出了遗传算法和BP神经网络相结合的风场短期风速预测模型,该模型具有预测精度高、收敛速度快的优点[10];陈耀武、汪乐宇等提出了基于神经网络、模糊聚类分析和模式识别理论,建立组合式神经网络的短期电力负载预测模型,该模型能够准确预测普通工作日及节假日的电力负载[11]。
神经网络BP学习算法具有逼近非线性连续映射的能力,广泛应用与非线性系统的建模及控制领域。但是BP神经网络存在一些缺点,主要是收敛速度慢,往往收敛于局部极小值,数值稳定性差,学习率、动量项系数和初始权值等参数难以调整。本文提出采用LM和SA混合算法,弥补了神经网络的缺点,并通过调整神经网络数量,最终得到较准确的车间生产工时达成率预测模型。
1 研究方法及理论
1.1 人工神经网络研究方法
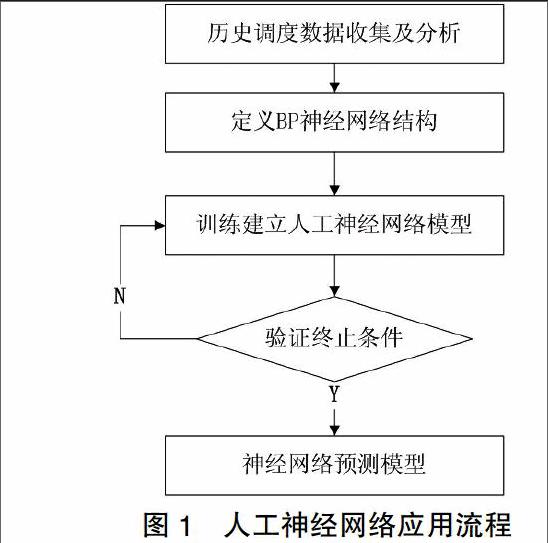
人工神经网络可以处理多元空间信息,成为模式识别、系统辨别、预测等功能的有力工具。人工神经网络的最主要的优点是不需要在训练之前明确定义近似函数。BP神经网络是最常用的神经网络,因为BP神经网络可以基于输入参数及输出参数计算出近似的仿真模型。基于人工神经网络的特性,它被广泛应用于寻找问题最优解。图1所示为BP人工神经网络解决问题的一般流程:
1)收集分析数据:收集大量数据,分析数据自身的相关性,找出主要参数作为输入。剔除数据中的奇异的,并将数据归一化用于训练神经网络。
2)选择网络类型与结构:根据问题的特点,选择神经网络为网络类型,并确定网络层数、每层节点数、初始权值、学习算法。其中隐含层的节点数选择比较麻烦,一般原则是在保证正确反应输入输出之间关系的基础上尽量少选隐含层节点数。
3)训练与验证:采用真实数据反复训练并验证神经网络直至得到合适的映射效果。在训练时初始权重可以随机产生,并且可取多组神经网络同时进行,通过取平均值来提高神经网络模型的准确性,该方法可以克服初始数据不充足的缺点。
4)对新数据实施预测,输出预测值。
1.2 SA\LM混合算法原理
人工神经网络中LM算法结合了高斯-牛顿法和最小梯度法的优点,包含了高斯-牛顿法的局部收敛性和梯度下降法的全局特性,它通过自适应调整阻尼因子达到局部收敛性,并且其迭代收敛速度高,可以补偿BP网络收敛速度慢的缺点[12],使其在很多非线性问题中得到稳定可靠解。但是初始值对LM算法的计算工程中具有很大的影响,若选取的初始值靠近真实值,在得到全局最优解的情景下减少运算时间,假设初始值的质量较差,优化结果会偏离全局最优解而得到局部最优解。通过两种方法可以解决该问题,一是采用尽量多的原始数据训练神经网络,使其具有较准确的预测能力,二是选择合理的优化算法与LM形成混合算法,消除其对初始值的高依赖性[13]。该研究对象为典型的离散生产型车间,无法获得所有的历史数据,第二种方式较合适。退火(SA)算法能够在算法执行过程中,基于较差初始函数值得到近似的最佳解决方案,这使得SA算法拥有在峰谷之间搜索找到全最小点的能力,无疑是最佳优化算法之一[14]。如图2所示为LM和SA混合算法在神经网络模型中的应用模式,首先基于有限的原始数据,采用SA算法训练神经网络预测模型,得到初始预测模型,将该模型中神经网络各层的权重矩阵及阀值作为LM算法的初始化参数,再次训练得到更优秀的神经网络预测模型。该混合算法能够捕捉并模拟车间排产员的经验知识和生产流程记录来形成制造过程中的系统知识,最终得到较优秀的车间调度模型。
2 人工神经网络结构
在50台加工系统组成的机加工车间中,有加工工人N人(工人充裕且有熟练度区分,其中有工序对应唯一工人),需要完成14个待加工零部件,每个工件都包含若干道工序,且工序流程一定。50台加工系统中包含车床组、铣床组、刨床组、钳床组、磨床组、焊接组,各组设备的加工能力一致, 以每个月该车间的工时达成率作为关键指标,工时达成率以实际完成工时与额定工时的比值为计算方式。车间调度员通过最佳的调度,并为各工序选配最佳资源,在满足设备加工能力及人员匹配的情况下获得最佳的工时达成率。
该调度问题有如下初始约束条件:1)任何设备无法同时加工超过两个工序;2)任意工件无法同时在多台设备上加工;3)工件必须严格按照工艺路线在指定机器上加工;4)除特定工序指定工人外忽略工人的熟练程度;5)工件的安装及拆卸时间已经包含在该工序的加工工时中;6)一般情况下有设备就有工人,除特殊情况工人处于充足状态;7)每个订单的14种原材料到位时间随机,遵循板材、管材、棒材的到位顺序。
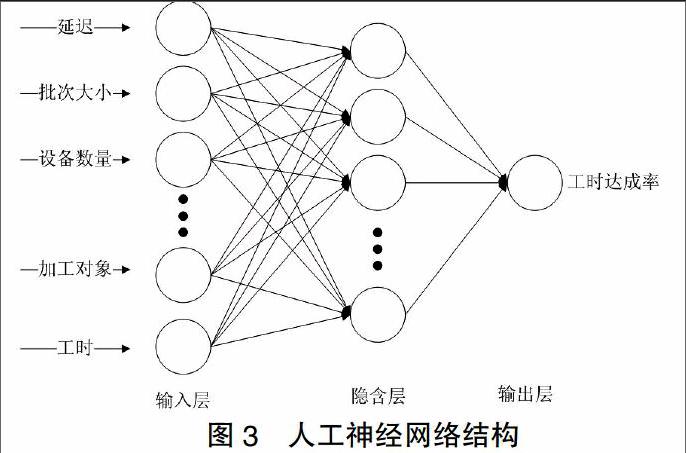
根据该车间调度问题的特点,定义人工神经网络的结构。神经网络的输入参数为各零件的加工对象、可用设备、设备数量、分批大小、延迟值、工时、前置工序耗时、后置工序耗时等210个参数,输出参数既目标函数为工时达成率。根据输入、输出参数的量确定采用两层神经网络结构,既一层隐含层一层输出层,并且隐含层包含10个节点,可保证获得全局最优的情况下避免出现过计算。图3所示为人工神经网络的总体结构,经过多次试验验证,该神经网络中核心参数如下:
网络层阈值参数biasConnect= [1;1],隐含层与输出层均有阈值;
输入层关系参数inputConnect = [1;0],输入层与隐含层有权值连接,与输出层无关系;
网络层关系参数layerConnect = [0 0;1 0],隐含层与输出层神经元相连;
输出层关系参数outputConnect = [0 1],输出层的神经元产生网络输出;
网络传递函数layers{1}.transferFcn= 'tansig',隐含层与输出层的传递函数;
隐含层初始函数layers{1}.initFcn = 'initnw',隐含层初始化函数;
训练算法参数trainFcn = 'trainlm',LM基础算法;
网络初始化函数initFcn = 'initlay',网络初始化函数;
神经网络数量参数networks=20、50、100。
3 预测结果及分析
54套历史数据作为训练验证样本并不能完全覆盖所有情景,本研究提出采用多神经网络并行计算求平均值的方法提高模型准确性。为了得到最准确的预测模型,神经网络数量和训练算法是本研究中优化对象。神经网络的训练算法主要以LM算法和SA\LM混合算法为研究对象,神经网络数量以20、50、100为研究对象。取54套样本中的51套为训练验证样本,3套为预测模型的测试数据,通过对比工时达成率预测值与真实值的均方差来判断神经网络模型的优异程度。训练数据中每套数据的210个参数生成51*210的矩阵,它们形象地表现出每个调度的输入与输出,这些矩阵将成为LM算法和SA\LM混合算法神经网络的输入参数,经过计算生成各自的神经网络预测模型,最后用3套调度方案去测试准确性,表1中显示了神经网络数为20、50、100的LM算法和SA\LM混合算法神经网络预测模型的测试结果。
从表1中清晰地显示了两种算法及三种不同神经网络数预测模型的预测误差,神经网络数量从20-50-100的梯度选择中预测模型的准确性误差呈8.46%-8.28%-6.87%的下降趋势,经过试验确定在该项目中采用100个神经网络数,该方法有效缓解了初始数据不充足的缺陷。图4中显示LM算法和LM\SA混合算法预测误差对比,其中LM算法预测误差均值为8.92%,LM\SA混合算法将该误差缩小到6.82%,证明混合算法能够通过改善LM单一算法中初始权重值及阀值,最终得到更优异的预测模型。
4 结论及展望
采用BP人工神经网络能够建立较准确的生产车间调度模型,并且使用SA算法建立人工神经网络的初始权重矩阵及初始阀值,再以LM算法进行优化的混合算法是建立车间调度模型的最佳算法;对于初始数据不充足的问题,可采用多神经网络并行计算求平均值的方法来提高模型准确性。得到较优秀的车间调度模型后,通过优化延迟值、批次大小、设备数量等输入参数可获得全局最优的工时达成率,最终输出离散车间效率最高的调度方案,这是今后的研究重点。
【参考文献】
[1]A.Azadeh, M. Jeihoonian, B. Maleki Shoja, S.h. Seyedmahmoudi. “An Integrated Neural Network–simulation Algorithm for Performance Optimisation of the Bi-criteria Two-stage Assembly Flow-shop Scheduling Problem with Stochastic Activities.” International Journal of Production Research 50.24(2012): 7271-7284[Z].
[2]Azadeh, Ali, Mohsen Moghaddam, Pegah Geranmayeh, Arash Naghavi. “A Flexible Artificial Neural Network–fuzzy Simulation Algorithm for Scheduling a Flow Shop with Multiple Processors.”The International Journal of Advanced Manufacturing Technology 50.5-8(2010): 699-715[Z].
[3]Golmohammadi, Davood. “A Neural Network Decision-making Model for Job-shop Scheduling.” International Journal of Production Research,51,17(2013): 5142-5157[Z].
[4]A.Azadeh, A. Negahban, M. Moghaddam. “A Hybrid Computer Simulation-artificial Neural Network Algorithm for Optimisation of Dispatching Rule Selection in Stochastic Job Shop Scheduling Problems.” International Journal of Production Research, 50, 2 (2011): 551-566[Z].
[5]Braglia, M. and Grassi, A., 2009. A new heuristic for the flowshop scheduling problem to minimize makespan and maximum tardiness. International Journal of Production Research, 47(1): 273-288[Z].
[6]祝翠玲,蒋志方,王强.基于B-P神经网络的环境空气质量预测模型[J]《计算机工程与应用,2007,22(43):223-227.
[7]陈廉清,郭建亮,杨勋,迟军,赵霞.基于进化神经网络的磨削粗糙度预测模型[J].计算机集成制造系统,2013,11(19):2855-2863.
[8]崔吉峰,乞建勋,杨尚东.基于粒子群改进BP神经网络的组合预测模型及其应用[J].中南大学学报,2009,1(40):190-194.
[9]张喜忠.基于神经网络预测模型的发动机异响信号提取研究[D].长春:吉林大学,2008.
[10]王德明,王莉,张广明.基于遗传BP神经网络的短期风速预测模型[J].浙江大学学报,2012,5(46):837-841.
[11]陈耀武,汪乐宇,龙洪玉.基于组合式神经网络的短期电力负荷预测模型[J].中国电机工程学报,2001,4(21):79-82.
[12]裴浩东.基于神经网络的稳态优化和控制研究[D].杭州:浙江大学,2001.
[13]董一芬. Levenberg-Marquardt神经网络算法研究[J].商场现代化,2009(3):385.
[14]J.R. Yang, W. Xu, M. Rajora, A.H. Shih, H.Z. Tan, L.W. Jin, H.F. Lou, S.Y. Liang,A hybrid neural network for prediction of flow shop scheduling performance, International Conference on Artificial Intelligence and Industrial Application, 2014, 081[Z].
[责任编辑:杨玉洁]
