真探究，让核心问题“增值”

□朱　宇



真探究，让核心问题“增值”

□朱宇

【摘要】要真正发挥核心问题的引领价值和建构功能，就需要从学生的学习实际出发，循序渐进地引领学生猜想、验证、阐释、建构、反思，让每一位学生都能够踏踏实实地经历深刻的探究历程。

【关键词】核心问题；探究活动；真实；深刻

在数学课堂教学中，我们经常针对学生的认知实际，在知识的关联处，方法的迁移处，学生的困惑处，提炼出既符合问题特征，又满足教学需要的核心问题。然而，有了核心问题，课堂教学效果就一定能够得到保证吗？

笔者以为，只有以核心问题为统领，以真实的探究活动为支撑，将学习过程作为知识的探索过程看待，时刻关注学生在探索学习中的活动体验与思维积淀，教学活动才能取得理想效果。

一、激发内在动机

维果茨基认为，教学的本质不在于“训练”、“强化”已经形成的内部心理机能，而在于激发、形成目前还不存在的心理机能，让学生产生主动参与的欲望。作为一种特殊的教学环境，情境的创设要能够激发学生的认知冲突，诱发其探究欲望和创造动机。

【案例1】“平行四边形的面积”

课始，出示面积接近的长方形和平行四边形纸片各一张（如下图），让学生想办法比较它们面积的大小。学生发现重叠不能比较大小，纷纷拿起直尺开始测量、计算。

在巡视中我发现，绝大多数学生都测量了两个图形的一组邻边，并列出了这样的式子：长方形面积6×4＝24平方厘米，平行四边形面积7×5＝35平方厘米。只有少数几个学生先测量平行四边形的底和高，再用“底×高”计算平行四边形的面积是7×3＝21平方厘米。悄悄问及缘由，原来他们课前看书预习过了。

在反馈交流过程中，多数学生赞同“7×5＝35平方厘米”这个计算方法，其理由是：因为平行四边形可以推拉变成长方形，长方形的长和宽就是平行四边形的一组邻边，所以平行四边形的面积计算公式就是“底×邻边”。很显然，这是长方形面积计算公式“负迁移”带来的错误结果，但是，这样的错误是在学生经历了自主思考的基础上产生的，而且他们是在根据自己的已有认知经验，主动探究解决问题。经历了这样一个真实的过程，学生会对计算平行四边形面积的体验和感悟更加深刻。学生最终收获的不只是一个简单的公式，还经历了根据目标制定、实施、调整探究策略的过程，促进了数学活动经验的积累以及对转化、类比等思想方法的感悟。

毫无疑问，平行四边形面积计算公式的推导是本节课的主要教学目标，相对应地，平行四边形的面积计算公式为什么是“底×高”，而不是“底×邻边”，这正是本节课的“大”问题。学生的“思”与“疑”，与这一核心问题不谋而合。两种算法的争执，唤起了学生的内在思考，增强了思维的活力，激发其强烈的探索欲望。

在上述活动中，通过自主尝试，不同的个体经验被激活，激发了学生在疑惑不解中“一探究竟”的强烈愿望，教师心中的教学目标也就不露痕迹地转化为学生自发的探究需要，探究之旅得以顺利启程。

二、丰富活动体验

探究动机被激发之后，学生就该和那些为探究活动准备的学习材料“亲密接触”了。这些材料是解决问题的必备素材，将要学习的新知识隐含其中，学生要通过对问题的界定与分析、材料的加工与整合，获得深刻体验，实现对所学知识的意义建构。

【案例2】“吨的认识”

与认识千克的直接体验不同，“吨”的认识只能让学生通过间接体验建立表象，例如抱一抱每袋10千克重的大米，通过“感受实物＋推算”的方式间接体验1吨有多重。然而，课堂上可以利用的素材毕竟是有限的，怎样组织学生进行体验活动，有效回答“1吨有多重”这样的核心问题呢？

首先是个人体验与共同体验的结合。先让每个儿童轮流搬一搬每袋10千克的大米，让每个学生都参与到这项体验活动中来，但是由于孩子们性别、力气大小等因素的差异，学生感觉各异，体验效果不是很明显。于是，老师叫上班里的“大力士”到台前搬，10千克、20千克、30千克，从“很轻松”到“不算太重”直至“吃不消了”，全班同学从大力士的语言、神态中真实地感受到了“30千克大米很重”。这时，老师却告诉他们：30千克已经很重了，可是这个重量与1吨相比可差远了！接着老师出示课件：3袋是30千克，5袋呢？10袋呢？像这样的100袋大米重量才是1吨。是啊，“3袋都搬不动了，100袋该有多重啊！”儿童从直观体验的基础上获得了“1吨很重很重”的间接体验。

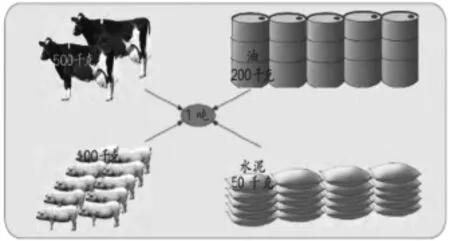
其次是分小组活动，将课堂有限空间内获得的感受向生活实际拓展。5个小组体验素材不同，一棵重1千克的大白菜，一袋重25千克的大米，一桶重10千克的水，1箱重5千克的大礼包，某一位体重30千克的学生。各组学生的体验方式也不尽相同：掂一掂，拎一拎，搬一般，抱一抱，但都通过估算或计算，结合生活中的某些具体事物，如游泳池里的水，卡车上的货物，特别是通过大礼包与大米的对比，间接渗透了重量与体积的辩证关系，各小组活动结果的汇报更让孩子们深刻体验了“1吨有多重”。

随后，教师出示一组图片，让学生算一算、画一画、比一比，进一步强化“吨”的重量表象的形成。

由上例可以看出，面对一个诸如“1吨有多重”的大问题，需要把握学生的认知心理，为他们提供一些喜闻乐见的学习素材，从一些细致入微的活动切入，让学生层层深入地深化活动体验，获得清晰认知。

三、展开深度思辨

数学探究活动的目的是促成学生认识过程的变化与知识建构，实现经验的自我提升。这个过程不会一帆风顺，特别是当学生第一次面对一个具有质变意义的知识时，探究之路注定不会平坦，教师应该组织学生自由争论，展开思辨，在思维质变处架设起从此岸到彼岸的桥梁。

【案例3】“三角形三边之间的关系”

课堂上，我给每个小组准备了两根一样长的纸条，要求剪开其中一根，通过自主操作来探究“如果两边之和等于第三边，能不能围成三角形呢”。没有想到，有的学生竟然“围成”了一个三角形！其实，这只是纸条有宽度带来的误差，几何意义上的“线”是没有粗细之分的。但是这么简单的原因却不能直接对学生解释，因为简单苍白的解释难以抵挡这貌似正确的结论。

我决定借助这个“节外生枝”的资源，引领学生进行冷静思考与深度思辨。我请这位学生到投影仪前放大“围成”的三角形，然后请其他同学发表看法:“他围的这个三角形，你同意吗？”经过投影放大，很多学生看出了“端倪”——只是沾了一点，并没有连上！于是纷纷表示“不同意”。那位学生试图动手调整，想让纸条完美地粘连到一起，但是总被同伴们指出“现在左边又分开了”“不能围成，还差一点点”。当然，另有部分学生为演示者出谋划策，提出要调整的地方，该生不断调整，但是最终也没有得到其他学生的认可。

最终，学生一致认为：永远不能围上，总是要差那么一点点。因为两边之和等于第三边，现在这样只能重合。接下来，借助动画演示刚才的辨析说理过程，学生发现总是差一点点，围不成三角形。

为什么要在这个知识点上花大气力组织细致入微的观察、辩论、分析？因为这是探究活动的一个重要节点，也是学生思维的困顿之处，需要引起全班学生的关注，将他们都卷入到对不同见解的思考、讨论中，让他们在澄清思维的过程中获得最大的思维成果。从表面上看，学生是在辩论“能不能围成三角形”，实质上他们是通过冷静的思考与激烈的争辩，真实经历对先前的错误想法进行自我否定的过程。我们认为，在否定意义上的肯定，会让探究活动更加有张力，探究活动也会因为互动而厚实。

探究活动并不只局限于操作层面，还应该及时组织学生通过同伴互助，在明理、析错的过程中相互启发思维，真正促进学生对探究成果的内省反思与深度思考。

四、构建知识网络

心理学研究成果发现，如果学生头脑中的知识是零散的和孤立的，那么堆积的知识越多，越不利于问题解决。只有让知识点按层次排列，呈现出一个层次网络系统，才能促进数学理解，提高解题能力，有利于知识的迁移。所以，在数学教学中，我们不仅要让学生掌握数学知识，而且还要使学生头脑中的数学知识网络化。

由于小学生对于知识的组织调控能力还不足，教师就要去引导学生把知识“点”连成“线”和“面”，体会知识点之间存在网络的结构，使头脑中的知识结构化、网络化。

【案例4】“平面图形的总复习”

学生经过一段时间的学习，对几何图形的认识已经有了一定的积累，复习课上，教师就不能仅仅简单再现单个的知识“点”，而应该把有关联的知识“串”起来，揭示它们之间的区别和联系，这样才能帮助学生真正实现知识的整理。

“平面图形的认识”复习课，目标之一就是通过整理和复习，使学生进一步掌握平面图形的特征，并以此沟通各个平面图形之间的联系。然而，要在短短的40分钟之内完成三角形、四边形和圆的特征复习，如果只作简单的知识再现，知识的容量可能是满满的，但是认知的结构是离散的。怎样引导学生将分散的知识进行整理沟通，使之系统化和结构化？

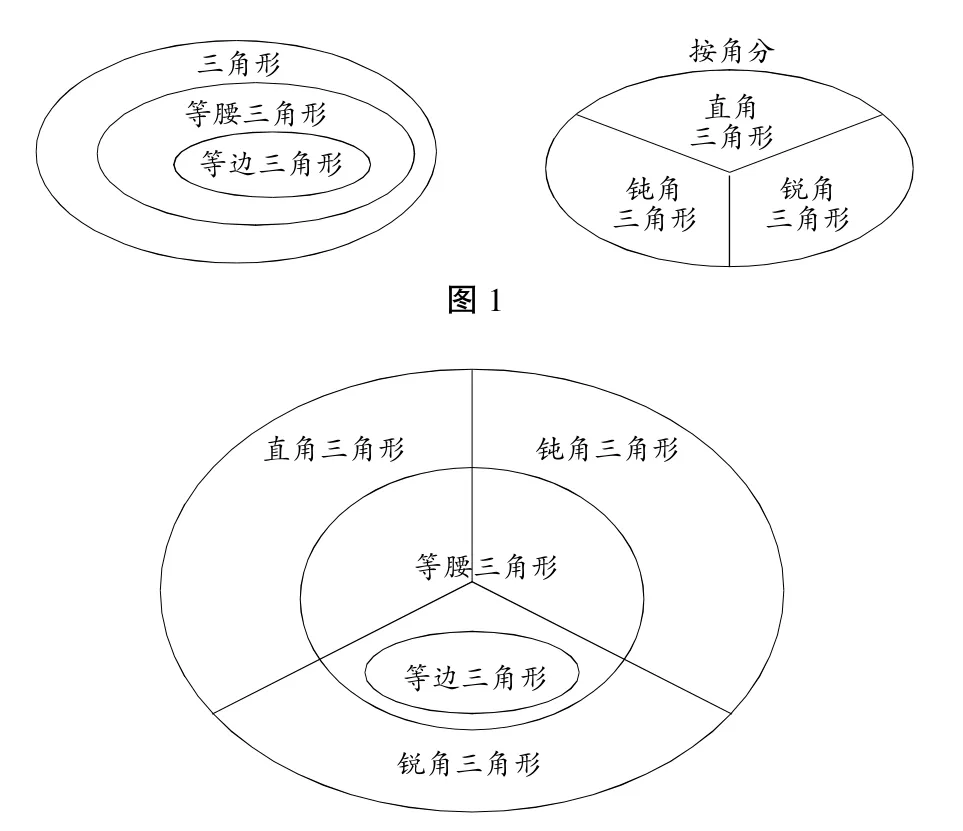
图2

课上，我出示了童趣十足的卡通图案，然后根据构成平面图形的基本要素——线和角，从“边”和“角”两个维度切入，提出与“分类”有关的核心问题，引导学生从图形的特征入手，逐步厘清图形之间的关系。“你认为这些图形可以分为哪几类呢？说一说你为什么这么分。”学生大多把这些图形分为三角形、四边形、五边形和圆4类。很显然，学生已经关注到了图形“边”的特征，但是分类的标准是不准确的。为了促进学生对图形特征认识的不断深化，我接着提问：“三角形、四边形都是由几条线段围成的，那么圆是由什么围成的呢？”学生的已有认知平衡打破，渐渐觉得之前的分类标准需要调整，继而主动提出把这些图形分成“直边图形”和“曲边图形”两类。

关于三角形的分类，通常都是局限在“按角分”和“按边分”这两种分类方法（如图1），这样的分类实际上是离散的，缺少“边”和“角”之间的关联。对此，我提出了本节课的第三个核心问题：“如果把等腰三角形和等边三角形也放进这个关系图里面，应该放在什么位置？”

这个问题，需要学生对各类三角形的概念、本质特征以及相互之间的联系与区别建立起清晰的认知，特别是既要满足角和边的各自特征，又要关注等边三角形和等腰三角形这样一种特殊的包含关系。最终学生将两幅图进行整合，得到了新的关系图（如图2）。对照这个合二为一的关系图，全班同学纷纷说出了自己的理解与发现：直角三角形、锐角三角形、钝角三角形当中可以有等腰三角形，而等边三角形只能是锐角三角形，等腰三角形中可以有直角和钝角……

几个关键问题的设计，引导学生不断地修正已有的片面认知，经历了由混沌到清晰、由粗疏到精致的思维过程，学生头脑中关于平面图形的认知由点状碎片发展为网状结构。问题的设计就是要聚焦知识“网”中的一个个节点，树立整体观念，以建构的思想统领复习过程，实现知识的整体建构。从这个意义上说，缺少了整体化的思想，数学探究性学习的内容就显得单薄和离散，学生的思维也显得被动和肤浅，不利于知识内化和学习能力的形成。

在数学学习活动中，我们将学习过程作为知识的探索过程看待，时刻关注学生在探索学习中的活动体验与思维积淀，要通过量少质优的核心问题，引领学生弄清知识的来龙去脉，从整体上把握知识结构，在自主探索的过程中理解和掌握数学知识，提升数学素养。

（组稿：朱宇编辑：胡璐）

【基金项目】本文系江苏省“十二五”教学研究课题“基于‘让学’理念的农村小学数学‘问题导学’研究”（课题批准号：2013JK10-L169）的阶段性成果。

中图分类号：G623.5

文献标识码：A

文章编号：1671-0568（2016）07-0033-03

作者简介：朱宇，小学高级教师，江苏省特级教师，江苏省“333高层次人才”培养工程培养对象，现就职于江苏省高邮市天山实验小学。