股价异常波动及波动集聚性——基于近似熵－小波变换的实证研究

郭建华

（邵阳学院，湖南 邵阳422000）



金融市场

股价异常波动及波动集聚性
——基于近似熵－小波变换的实证研究

郭建华

（邵阳学院，湖南 邵阳422000）

摘要：以2001年1月1日至2015年7月31日上证综指日收盘价为样本，运用近似熵-小波变换方法，对上证综指时间序列进行了多尺度复杂性分析。通过计算样本数据序列的近似熵值发现，股票市场的波动性与股指时间序列的近似熵值密切相关：近似熵值越大，股市波动性越大。通过引入小波变换对近似熵序列进行分解和重构，发现股价波动具有阶段聚集性，而且股价变化过程中的异常波动伴随着重大经济事件或突发事件而发生。

关键词：近似熵；小波变换；股价波动；波动集聚性

股市异常波动即股价的大幅度、不连续变动。预料之外的重大信息发布（如股票分红、公司兼并、宏观经济政策调整）和突发事件的发生都会引起市场的异常波动，表现为股价的跳跃变化。理论和实践研究表明，不同于股价的连续变化或小幅波动，股价异常波动有其在金融领域上的显著含义，异常波动反映的是市场变化的不稳定性和复杂性，隐含的是市场风险，股价演化进程中的异常波动检测和识别是风险度量与风险管理的出发点。[1]

一、文献综述

很多学者对股价异常波动的检验方法进行了研究。如Barndorff-Nielsen and N.Shephard（2006）提出双幂变差检验；[2]Lee and Mykland（2008）提出非参数滚动检验；[3]At-Sahalia and Jacod（2009）提出基于不同数据频率计算截取幂变差的价格跳跃检验；[4，5]Yi Xue等（2014）基于小波变换方法，利用高频数据对股市跳跃变化进行了检测；[6]Limiao Bai等（2015）基于系统适应框架理论，并利用小波方法对欧洲、美国和中国大陆股票市场的突变性进行了研究。[7]

近年来，国内学者发现我国股市存在明显的异常波动，如陈浪南、孙坚强（2010）[8]，欧丽莎、袁琛、李汉东（2011）[9]，沈根祥（2012）[10]等。也有很多学者运用参数模型对股价变化过程中存在的跳跃现象进行检测。如郭文旌等（2013）应用动态Jump-Garch模型进行股价跳跃行为检测，并分析了股价跳跃现象和重大事件的关联性；[11]黄苒和唐齐鸣（2014）通过构建门限效应下状态变量依赖自回归强度跳跃-GARCH模型，对我国股市跳跃现象进行了研究，并通过对不同类型中国上市公司股票市场数据的实证分析，表明该模型对各类上市公司股票资产价格跳跃特征都具有较好的辨别和预测能力；[12]赵涤非和唐勇（2015）则借助跳跃强度模型，从经济信息释放对跳跃影响的角度，探讨了上证综指跳跃现象产生的原因。[13]

从现有研究看，国内外学者大多是通过参数模型的设定进行股价异常波动行为的检测研究，关于非参数方法进行股价异常波动检测的研究文献甚少。近年来，有学者从系统动力学结构突变的角度出发，引入了近似熵方法，为时间序列的突变分析提供了新的途径。近似熵（Approximate entropy，简称ApEn）是最近发展起来的一种度量序列的复杂性和统计量化的规则。它是在20世纪90年代由Pincus为了克服混沌现象中求解熵的困难而提出的。[14]他根据K氏熵的定义，将近似熵定义为相似向量在由m维变化到m+1维时保持相似性的条件概率，其物理意义是维数变化引起新模式产生的概率大小，近似熵值越大，序列越复杂，产生新模式的概率越大。[15]近似熵方法具有所需数据量小、抗噪能力强、检测结果准确等优点，该方法在医学、交通流预测、水文气象突变和故障检测等方面得到诸多应用。如，郭兴明等基于定量递归分析和近似熵对心音信号进行分类识别。[16]张亮亮等基于近似熵对北京四环一路段的交通流序列趋势进行了检测。[17]何文平[18]，孙永东等[19]基于近似熵对降水突变情况进行了分析。张振海等利用模糊近似熵方法对传感网数据故障进行了检测。[20]

综上所述，近似熵方法在医学、水文气象、工程故障检测等方面有了较为广泛的应用。然而，据作者所掌握的文献来看，关于近似熵方法在金融时间序列变化尤其是股价异常波动分析方面的应用甚少。为此，本文首先采用近似熵计算分析股价变化的复杂性和股价的异常波动，然后引入小波变换对近似熵序列进行分解和重构，探究股价发生异常波动的内在原因。

二、研究方法

（一）近似熵（ApEn）

近似熵具有对确定性信号和随机信号都有效的特点，其基本原理是用一个非负数来表示时间序列的复杂性，时间序列越复杂，对应的近似熵值也越大。[14]换言之，近似熵是从序列复杂性的角度来度量数据序列发生模式改变的概率大小，产生新模式的概率越大，近似熵值越大，说明系统越趋近于随机状态，系统越复杂；反之，近似熵值越小则表明数据信号越平稳。

设{x（i）；i=1，2，…，n}表示样本数据序列，则基于样本数据的近似熵（ApEn）可以按如下步骤求得：

（1）针对{x（i）；i=1，2，…，n}构建m（>0）维向量：

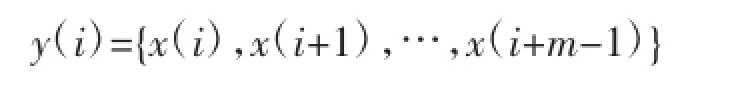
（2）对坌i，j（=1，2，…，n)，定义向量y（i）和y（j）的欧氏距离为：

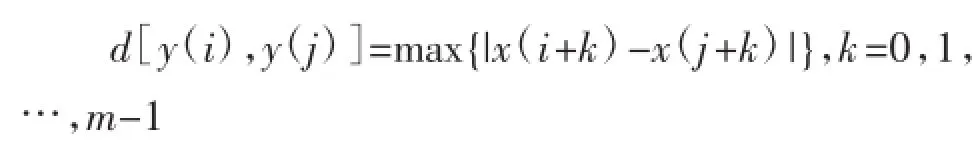
（3）给定容许偏差r（r>0），对i=1，2，…，n-m+ 1，计算：

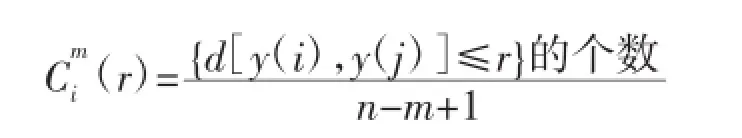
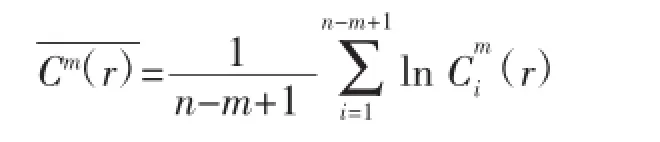
（6）对样本序列{x（i）；i=1，2，…，n}的近似熵定义为：

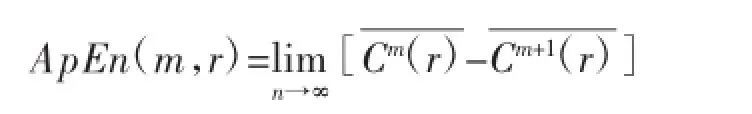
给定样本长度参数n，则有：

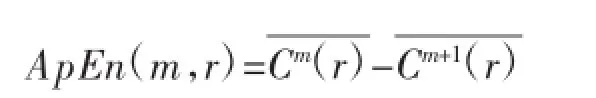
从近似熵的计算过程来看，对给定的样本数据序列，近似熵的大小受m和r的影响，实际应用中，一般取m=2，r=0.1滓～0.25滓（滓表示样本标准差）。[14]

根据近似熵值的计算原理可知，各阶段的近似熵值反映数据序列在各时段保持自相似性的能力，平稳数据序列对应的近似熵值也相对稳定，数据发生突变时近似熵值也会随之发生显著的变化。据此，我们可以通过采用滑动窗口法从原数据序列选取不同子序列，计算各子序列的近似熵，通过检验近似熵值的显著变化进行数据异常波动性分析。具体步骤如下：

（1）选择滑动窗口长度l、滑动步长h以及m，r。

（2）对每个i-1，…，n-l+1，选取子序列：{x（i），x（i+1），…，x（i+l-1）}。

（3）计算子序列的近似熵。

（4）保持窗口长度l不变，以滑动步长h移动窗口，重复步骤（2）～（3）。这样，可以得到一个长度为n-l+1的近似熵序列。

根据动力学理论，具有相同动力学结构的时间序列的复杂性差异不大，[17]对上述近似熵序列进行检验，如果近似熵序列值在某一点开始发生显著变化时，则可以认为该点就是时间序列变化趋势的转折点，即异常波动点。

（二）小波变换（WT）

本文中，我们采用 Mallat算法[21]对近似熵ApEn序列进行小波分解和重构，分析股市异常波动情况。具体算法如下：

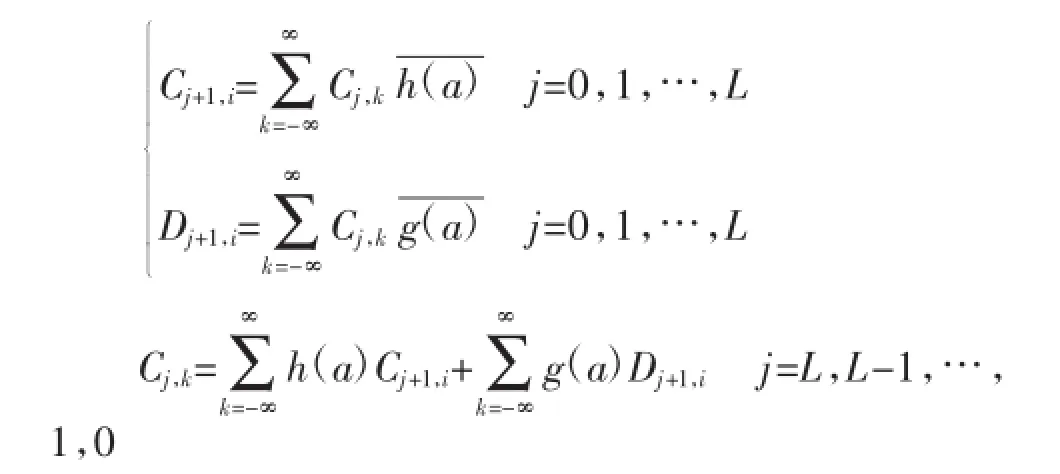
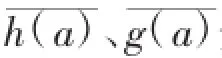
三、实证分析

相对西方发达国家的证券市场，我国股票市场的发展历史较短，市场相对不成熟而且投机色彩浓厚，因而市场价格波动相对较大，甚至因为受外部因素的影响常常伴随有异常波动现象，而股价异常波动正是股市风险的体现。因此，本文对股价异常波动进行研究，以便为监管者完善市场交易机制和投资者进行风险管理提供一定的参考依据。

（一）样本数据及初步统计分析

本文的样本数据选取了上证综合指数的日收盘价格，时间跨度为2001年1月1日至2015年7 月31日，涵盖了2007年前后一个完整的牛熊市轮回。数据来自“网易财经——行情中心”。

表1是上证综指样本数据的日涨跌幅度概况，在整个样本期内，指数日波动超过1%、3%、5%的天数分别为1122天、179天、55天，分别占样本期的31.77%、5.07%、1.56%。由此看来，我国股市的波动现象较为频繁。

从样本数据统计结果可以看出：指数大幅波动时常发生，而且主要集中在2007～2009年和2014年下半年至2015年上半年，这两个时段刚好是经历了中国股市罕见的牛熊市大轮回，各路资金涌入股市，市场情绪高涨，当然，也有其他诸多因素影响股市大幅波动。

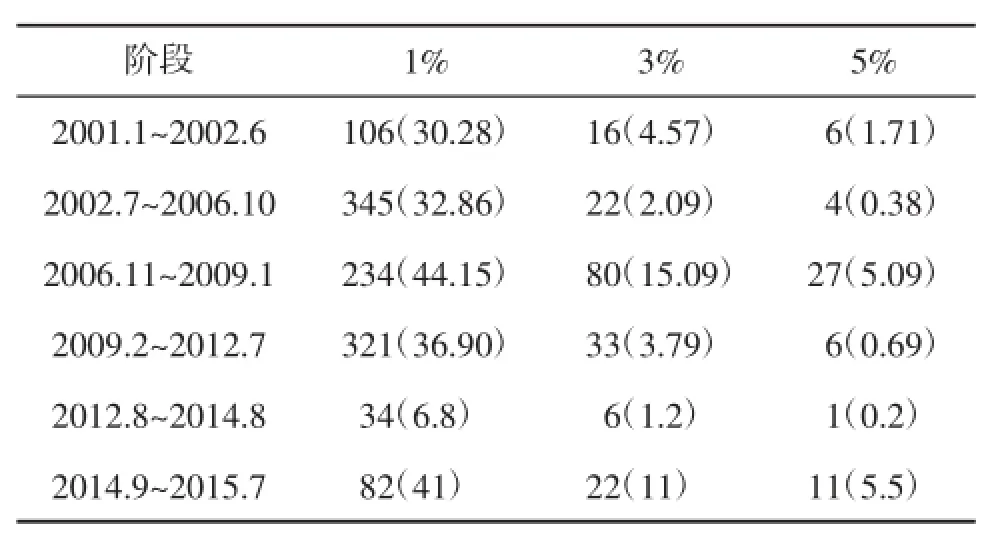
表1　上证综指分时段日波动幅度概况（括弧内数字表示阶段内占比：%）

（二）上证综合指数的近似熵序列分析

基于一年正常交易天数为252天，一周正常交易天数为5天，对上证综合指数日数据，我们首先分别选取滑动窗口长度l=252天和滑动步长h=5天（也可根据需要，调整滑动窗口长度和滑动步长），m=2，r=0.25滓，按照近似熵（ApEn）方法的步骤（1）～（6）计算，结果如图1-1所示。

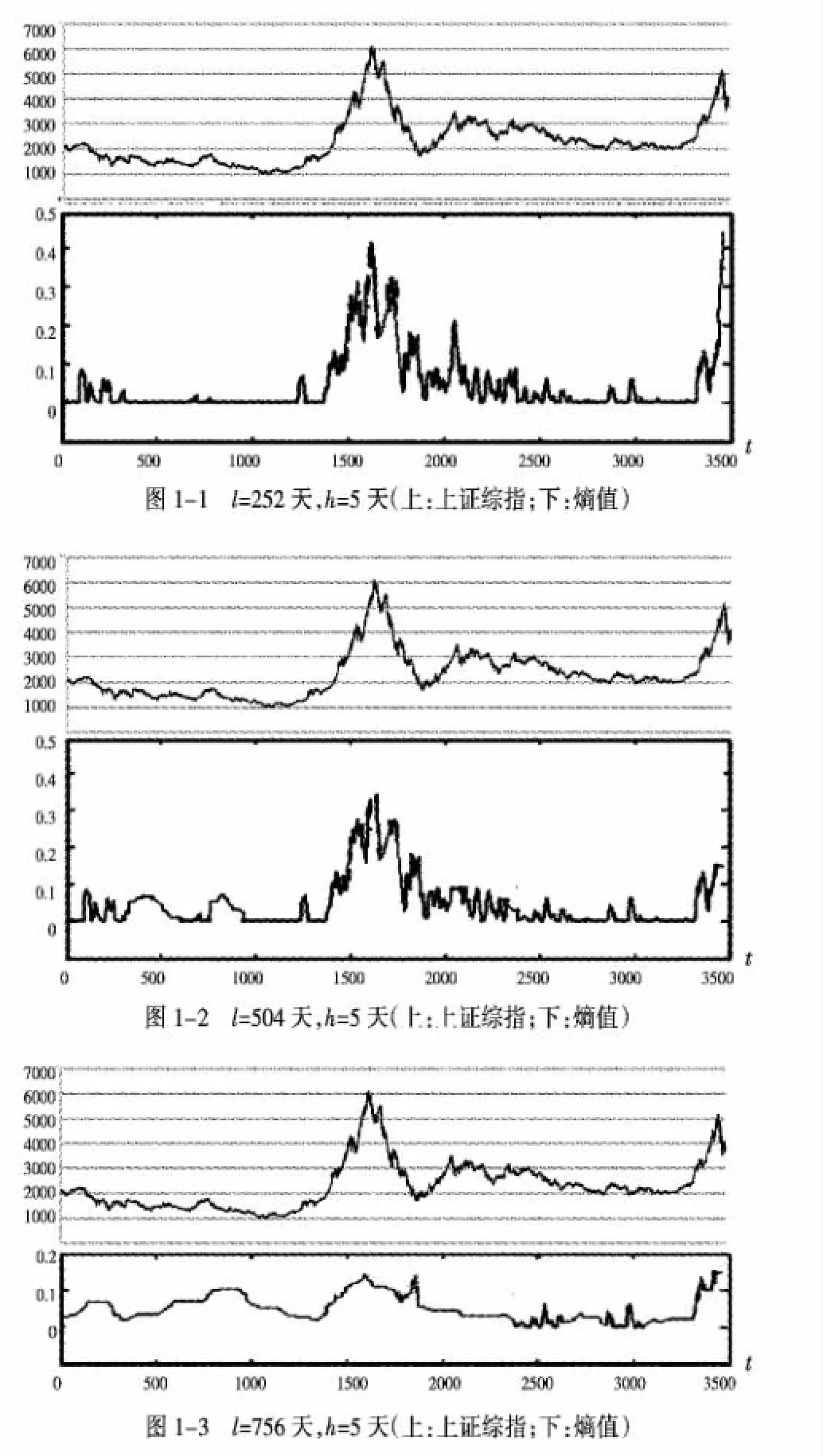
图1　上证综指及ApEn值序列图

由图1-1可知，上证综合指数在不同时段呈现出不同的波动特征，尤其是在2007年的牛熊市轮回阶段，波动特征更明显。具体来说，上证综合指数的ApEn值大体呈现出六个阶段性的变化过程，分别为：（1）第一阶段t=1～350（对应于2001年1月至2002年6月）。该阶段近似熵值尽管不大，但变化不平稳，这表明上证综合指数有一定的波动性，事实上，从图1-1（上）可以看出，该阶段的上证综合指数从2200点跌至1400点，波动幅度达700多点。（2）第二阶段t=351～1400（对应2002年7月至2006年10月）。该阶段近似熵值较小而且平稳变化，表明上证综合指数波动性不强，图1-1（上）也表明上证综合指数基本位于1400点与1700点的振荡区间波动，变化相对平稳。（3）第三阶段t= 1401～1930（对应2006年11月至2009年1月）。该阶段近似熵值很大而且变化极不稳定，表明上证综合指数处于剧烈波动时期，该阶段正好是2007年前后的牛熊市轮回阶段，指数值在不到一年的时间从1800点蹿升至6092点，又在一年时间内跌至1900点，如此大幅波动可谓绝无仅有。（4）第四阶段t=1931～2800（对应2009年2月至2012年7月）。该阶段近似熵值较大也不平稳，表明上证综合指数处于较大幅度波动期，事实上，该阶段上证综指涨跌幅度达1200点。（5）第五阶段t=2801～3300（对应2012年8月至2014年8月）。该阶段上证综合指数基本位于2000点至2300点的区间震荡，波动很小，从图1-1（下）的近似熵序列图也可以看出，该阶段的近似熵值较小且变化平稳。（6）第六阶段t= 3301～3530（对应2014年9月至2015年7月）。该阶段的近似熵值较大而且变化不平稳，说明上证综合指数处于较强波动期，图1-1（上）的指数序列图也说明了这种波动特征，事实上，该阶段的上证综合指数值在不到一年的时间内从2300点突涨至5166点，而后迅速跌至3600点，波动剧烈。总之，近似熵值及其变化特征与上证综合指数的变化关系如表2所示。表2的结果与表1的统计分析结果基本一致。由此看来，近似熵确实可用于对时间序列的波动性研究，是检测股市波动的良好工具。

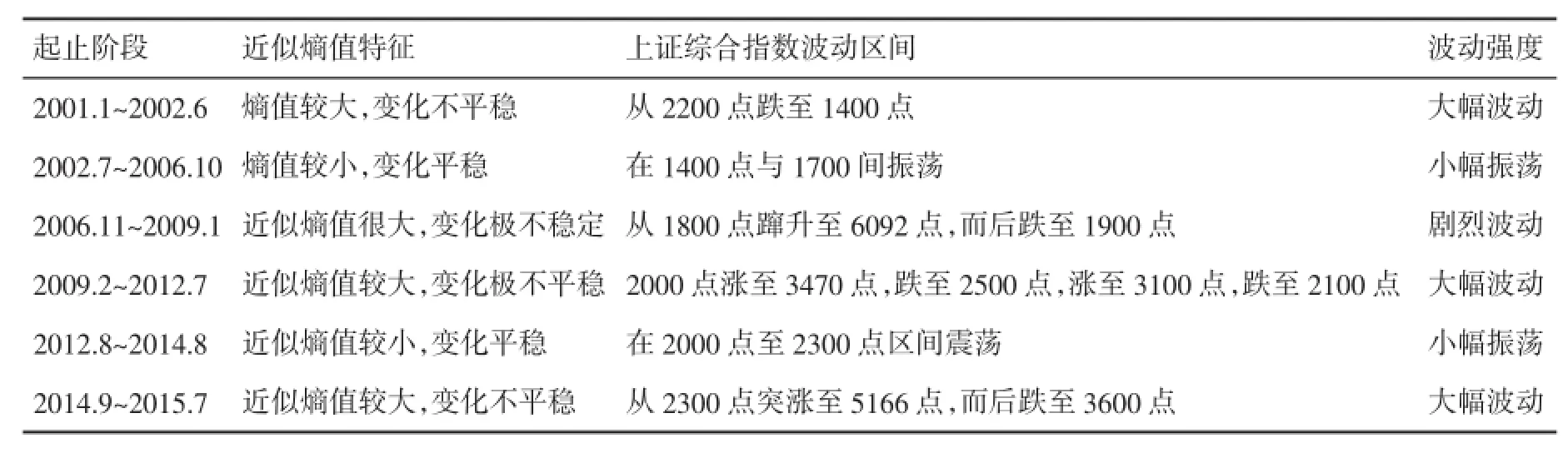
表2　上证综合指数阶段性波动及近似熵值

由此看来，对投资者来说，大且变化不平稳的熵值，意味着股价异常波动，需谨慎投资，对监管部门来说，需要加强市场监管，尽量避免大幅涨跌的发生而影响市场的正常运行；反之，小且平稳变化的熵值，说明股价相对平稳，是投资的可选时机。

考虑到ApEn检测结果与滑动窗口选取的长度有关，选择的窗口长度过大或过小都会对检测结果造成一定的影响。[22]在此，我们就滑动窗口长度l和滑动步长h对ApEn检测结果的影响进行分析。首先假定l或h中的一个固定不变，对另一个进行调整以检测其对ApEn值的影响。譬如检验滑动窗口长度l对检测结果的影响时，则假定滑动步长h不变，分别选取l=504天和l=756天，结果如图1-2和图1-3所示。由此可以发现，对于固定的滑动步长h，在l=504天的ApEn值的变化规律和l=252天的结果基本一致，原始数据序列异常波动的检验结果较为稳定。但如果滑动窗口长度过大，如图1-3中当l=756天时，数据序列熵值的阶段性变化不明显，从而难以检测异常波动点。由此看来，合理选择滑动窗口长度对于数据序列异常波动检测结果准确与否具有重要意义。实践中，通常首先选取较长的滑动窗口长度检测序列的异常波动点或异常波动区间的大致范围，然后逐步缩小窗口长度，直到数据序列异常波动点或异常波动区域稳定为止。对于上证综合指数序列的异常波动检测来说，建议取滑动窗口长度l=252天或l=504天，在此滑动窗口长度下，通过计算序列的ApEn值，能够较好地识别波动情况。同样，滑动步长h的选取也不宜过长或过短，滑动步长过长容易造成异常波动点的淹没；反之，滑动步长过短则导致计算量过大。

（三）近似熵序列的小波变换分析

为了进一步分析上证综合指数波动变化及其影响因素，我们基于小波变换中Symlets小波基中的sym8，利用Matlab R2009a中的“小波分析”工具包对l=252天和h=5天的ApEn熵序列进行多尺度分解分析。首先对熵值序列进行初步小波分析发现，小波分解的低频系数对应的是数据信号在最高尺度的加权平均，反映的是信号的总体趋势，其变化规律类似于原始信号数据；高频系数对应的则是信号加权平均的广义差分，代表的是数据信号在不同分解尺度的波动细节。我们对上证综合指数日数据序列的近似熵分解重构得到6个高频分量，每个分量表示了不同时间尺度上的股市变化情况。结果如图2所示。

在图2中，上证综合指数近似熵值的sym8分解得到的d5分量的演变趋势特征和近似熵值演变的变化规律基本一致，反映了近似演变的平均状态。说明上证综合指数的周期波动性与d5这一时间尺度的上证综合指数变率有密切关系，所以这种密切关系可能也就是周期性“波动集聚”效应的体现。另外，我们选择的样本中包括了2007年前后的牛熊市轮回和2014年下半年的股市大涨时期，数据具有一定的对称性。从图1的熵值序列图和图2的小波分解图也可以看出，在牛熊市轮回和股市大幅涨跌前后（第一、三、四、六阶段），股市波动显著增大。

接下来进一步对异常波动点进行分析，数据信号中异常波动点的位置，可能反映在小波变换的过零点或者小波变换的峰值点上。然而过零点极容易受白噪声的干扰，根据小波变换峰值点检测信号异常波动较为稳健，所以我们仅对小波变换系数峰值点以及峰值点之间的过零点进行统计，寻找上证综合指数的异常波动点。表3是运用近似熵－小波变换分析检测到不同时段上证综合指数部分异常波动点的具体发生时间及对应的波动原因（重大经济事件或突发事件）。

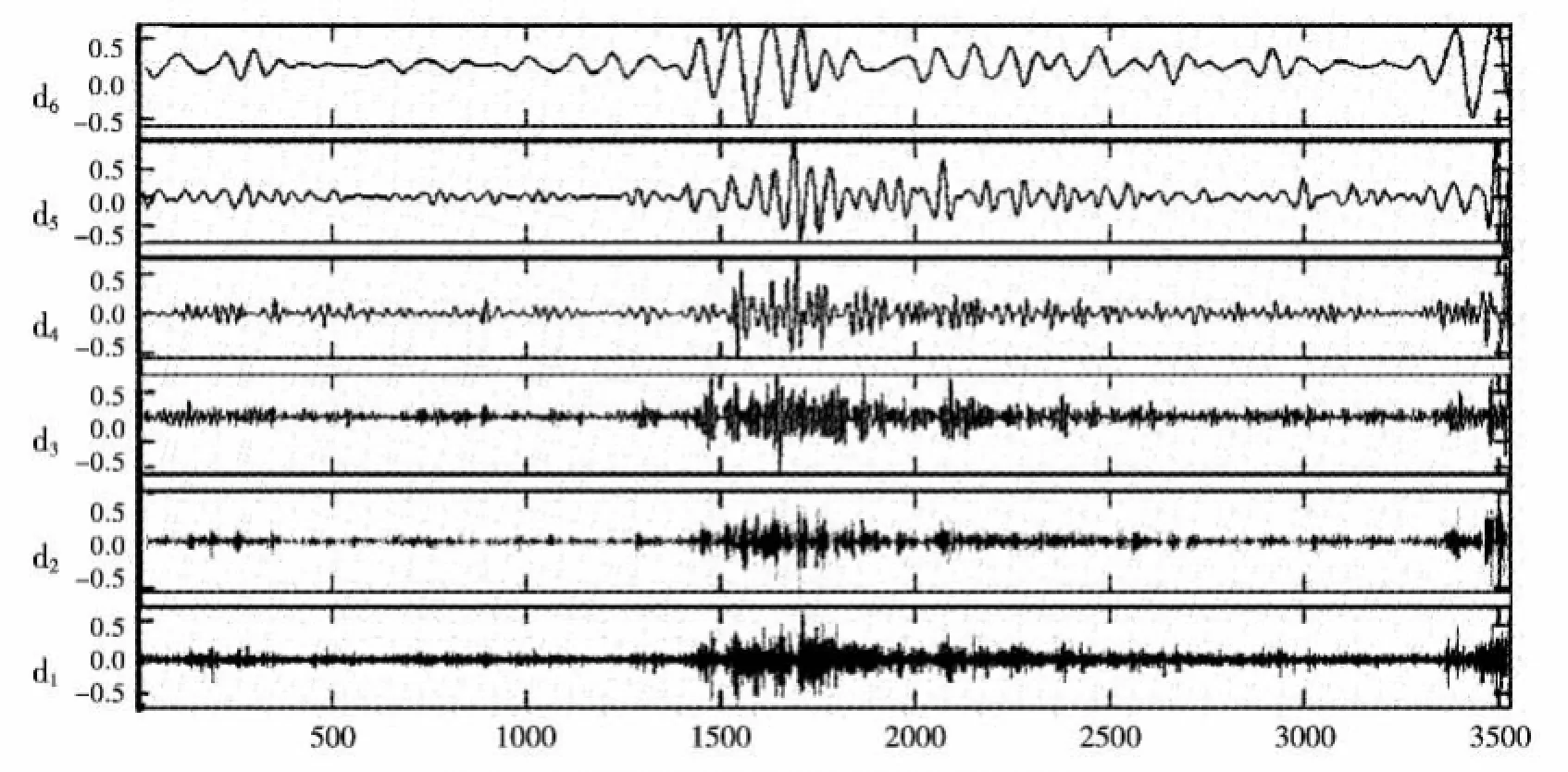
图2　上证综合指数近似熵值得小波分解

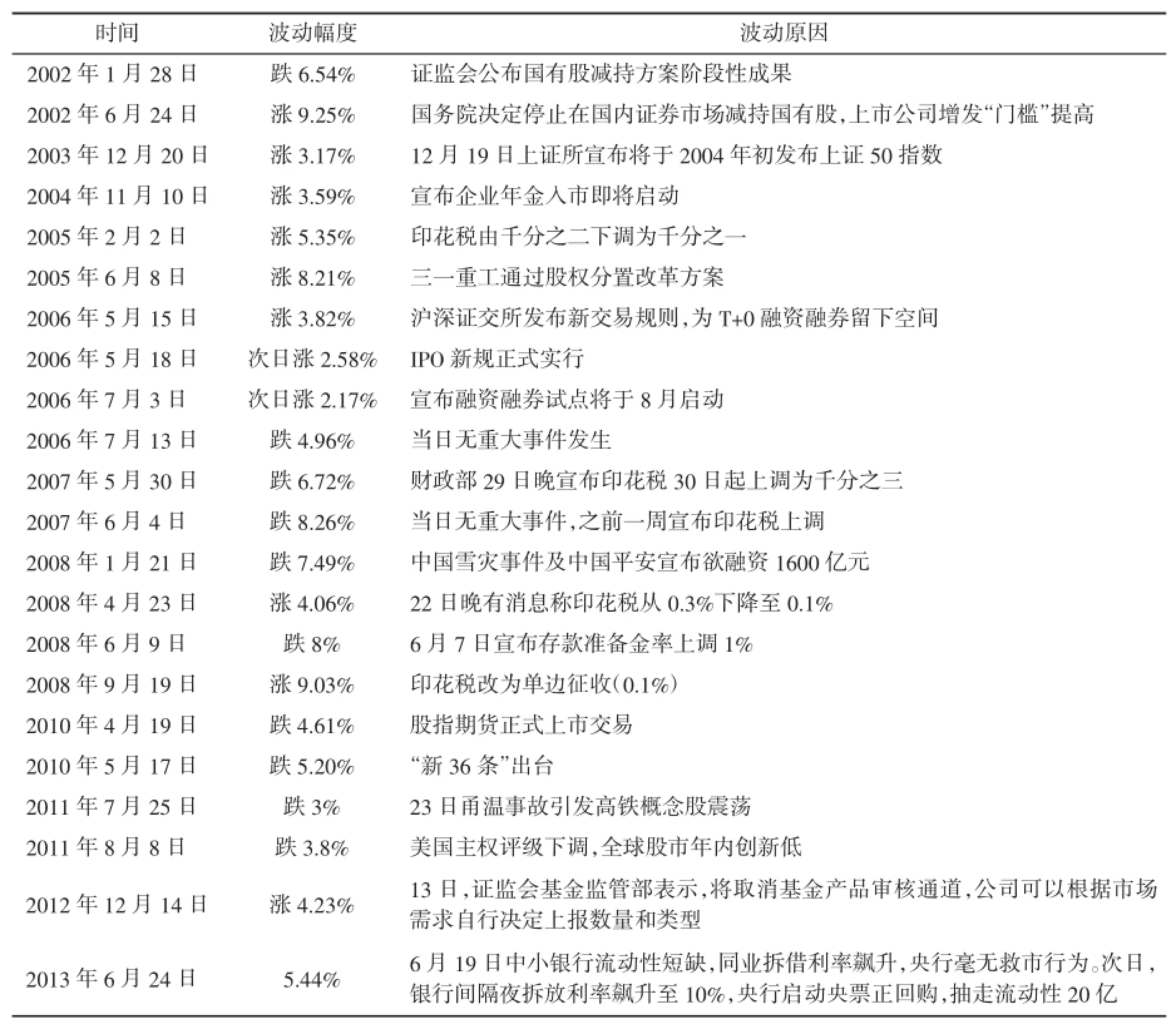
表3　上证综合指数异常波动时间及波动原因

四、结论

股市是一个国家或地区实体经济运行的晴雨表，实体经济的运行趋势和状态变动很容易导致股票市场的异常波动，因此检测股市运行过程中的异常点，为研究金融危机预警提供了依据。本文基于近似熵和小波变换相结合的金融时间序列异常波动分析，研究结果表明：

第一，与现有关于股价异常波动研究文献相比，近似熵－小波变换方法不仅可以得到股价在不同时间尺度和不同阶段的波动特征，还可以揭示股价发生异常波动的内在演变机理和辨别诱发异常波动的外在宏观因素。

第二，近似熵值与股价时间序列的幅值变化无关，对数据序列的分析效果优于均值、方差、标准差等统计参数。相对于参数方法，近似熵方法无需繁琐的参数设定和估计，而且通过滑动窗口技术，近似熵要求的数据量小，具有较强的抗噪和抗干扰能力等优点。

第三，从实证分析结果看，近似熵值的变化确实反映了股价的实际波动情况，无论是对监管部门还是投资者，都具有较好的参考价值。当近似熵值增大且不平稳变化时，说明股价有大幅波动，对监管机构来说，应该加强市场监管，分析波动原因；对投资者而言，应该谨慎投资。反之，近似熵值较小且平稳变化，说明股价相对平稳，波动较小，是投资的可选时机。

第四，样本数据序列近似熵值的计算结果受滑动窗口长度和滑动步长的影响，目前关于滑动窗口长度和滑动步长的确定没有成熟的理论依据，主要通过人工调整和试算来确定，如何从理论上确定滑动窗口长度和滑动步长或通过计算机优选确定是一个值得思考的问题，也是一个具有理论研究价值和实际应用价值的课题。

参考文献：

［1］Duffie D.，and Pan Jun.Analytical value at risk with jumps and credit risk［J］.Finance and stochastics，2001（5）：155-180.

［2］O.E.Barndorff-Nielsen and N.Shephard.Econometrics of testing for jumps in financial economics using bipower variation［J］. Journal of Financial Econometrics，2006，4（1）：1-30.

［3］Lee，S.S.，Mykland，P.A.Jumps in financial markets：A new nonparametric test and jump dynamics［J］.Review of financial studies，2008，21（6）：25-35.

［6］Xue，Yi，Ramazan Genay，and Stephen Fa gan.Jump detection with wavelets for high-frequency financial time series［J］.Quantitative Finance，2014，14（8）：1427-1444.

［7］Bai L.，Yan S.，Zheng X.，&Chen B.M.Market turning points forecasting using wavelet analysis［J］.Physica A：Statistical Mechanics and its Applications，2015，437：184-197.

［8］陈浪南，孙坚强.股票市场资产收益的跳跃行为研究［J］.经济研究，2010（4）：54-66.

［9］欧丽莎，袁琛，李汉东.中国股票价格跳跃实证研究［J］.管理科学学报，2011（9）：60-66.

［10］沈根祥.沪深300指数跳的逐点检验及动态分析［J］.中国管理科学，2012（1）：43-50.

［11］郭文旌，邓明光，董琦.重大事件下中国股市的跳跃特征［J］.系统工程理论与实践，2013，33（2）：308-316.

［12］黄苒，唐齐鸣.基于可变强度跳跃-GARCH模型的资产价格跳跃行为分析——以中国上市公司股票市场数据为例［J］.中国管理科学，2014，22（6）：1-9.

［13］赵涤非，唐勇.基于高频数据视角的上证综指跳跃原因分析［J］.系统科学与数学，2015，35（1）：85-98.

［14］Pincus S.M.Approximate entropy（ApEn）as a complexity measure［J］.Chaos，1995，5（1）：110-117.

［15］张艳艳.近似熵理论及应用J］.中国医学物理学杂志，2009，26 （6）：1543-1546.

［16］郭兴明，李传鹏，卢德林.定量递归分析和近似熵在心音分类识别中的应用［J］.数据采集与处理，2013，28（5）：559-564.

［17］张亮亮，贾元华，牛忠海，廖成.基于近似熵的交通流序列趋势变化检测［J］.北京交通大学学报，2014，38（6）：7-11.

［18］何文平.基于近似熵的突变检测新方法［J］.物理学报，2011，60 （4）：1-8.

［19］孙永东，张洪波.近似熵和小波变换在降水突变分析中的应用［J］.水电能源科学，2015，33（6）：15-18.

［20］张振海，李士宁，李志刚.相关近似熵及在传感网数据故障检测中的应用［J］.华中科技大学学报（自然科学版），2016（2）：86－91.

［21］刘明才.小波分析及其应用［M］.北京：清华大学出版社，2005.

［22］王启光，张增平.近似熵检测气候突变的研究［J］.物理学报，2008，57（3）：1976-1983.

（责任编辑：龙会芳；校对：卢艳茹）

Abnormal Volatility and Volatility Clustering of Stock Price——an Empirical Study Based on Approximate Entropy and Wavelet Transform

Guo Jianhua

（Shaoyang University,Shaoyang 422000,China）

Abstract:The paper selected daily closing price of shanghai composite index from January 1st 2001 to July 31st 2015 as samples,adopted the method of approximate entropy of wavelet transform and carried out multi-scale analysis of the time series of Shanghai Composite Index’complexity.After calculating data series’approximate entropy,it could be concluded that there is a close connection between stock market volatility and approximate entropy of stock index’s time series.The greater the approximate entropy is,the more volatile of the stock market will be. Through the introduction of wavelet transform,the paper tries to disintegrate and rebuild approximate entropy series,and discovers that there are phased clustering with the stock price volatility.And the occurrence of abnormal volatility of stock price is always accompanied with major economic incidents or emergent incidents.

Key words:approximate entropy;wavelet transform;volatility of stock price;volatility clustering

中图分类号：F224

文献标识码：A

文章编号：1006－3544（2016）03－0039－07

收稿日期：2016-03-11

基金项目：教育部人文社会科学研究青年基金项目（15YJC630026）；湖南省教育厅资助科研项目（14B160）

作者简介：郭建华（1975-），男，湖南邵阳人，博士，邵阳学院副教授，研究方向为金融风险管理。