关于不定积分解题方法的探讨

韩艳娜

(商丘学院 计算机工程学院，河南 商丘 476000)



关于不定积分解题方法的探讨

韩艳娜

(商丘学院 计算机工程学院，河南 商丘 476000)

摘要：分析不定积分的直接积分法、换元积分法和分部积分法的解题方法，可以帮助学生更好地掌握不定积分的求解方法.通过实例对一道不定积分题用了多种方法求解，使学生更灵活地掌握这些方法.

关键词：不定积分；直接积分法；换元积分法；分部积分法

0引言

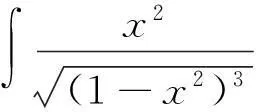
1直接积分法

适用对象：该方法只能求出很少一部分比较简单的函数的不定积分.

处理方法：被积函数经过整理、恒等变形后能够根据不定积分运算法则和不定积分公式直接写出原函数.

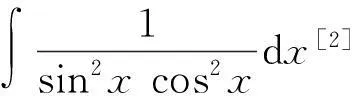
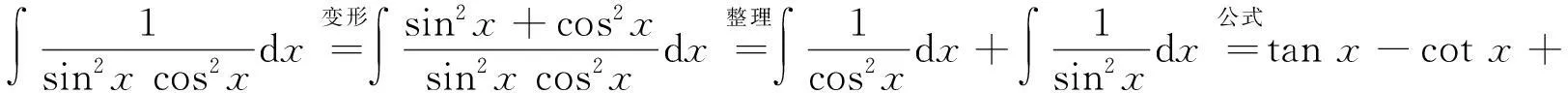
2换元积分法

换元积分法就是通过适当的变量代换，把积分转化为积分表中的类型或容易积分的形式[3].

2.1第一类换元积分法

第一类换元积分法又称凑微分法，它通过引入中间变量u=φ(x)，把原来对自变量x的积分变为对中间变量u的积分[4]：

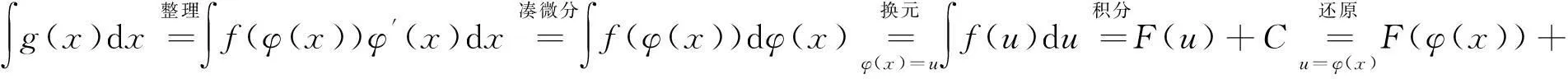
适用对象：主要用于被积函数是复合函数的不定积分.

处理方法：在求积分时，应先找复合函数的中间变量u=φ(x)，把中间变量的微分du=φ′(x)dx“凑”出来，把被积函数由自变量为x的复合函数转化为自变量为u的单一函数，再根据直接积分法得F(u)+C，最后再将u换回φ(x)即可.

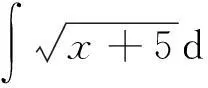
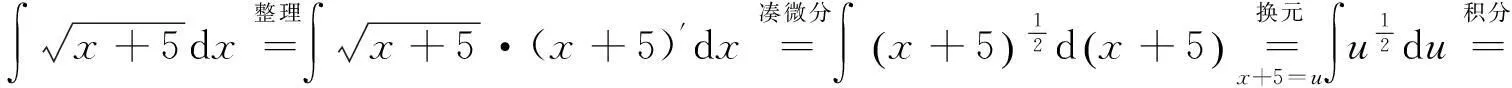
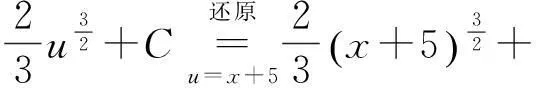
2.2第二类换元积分法

第二类换元积分法又称变量代换法，引入变量x=φ(t)，把原来关于自变量x的积分转化为关于新自变量t的积分.

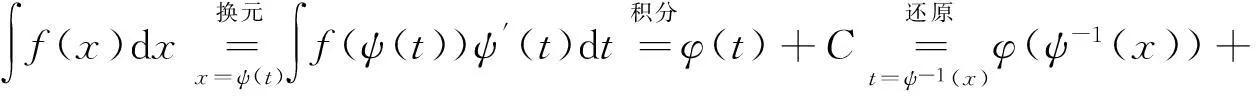
适用对象：主要适用于被积函数中含有根式的不定积分，通过变量代换把根式消去.

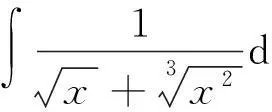
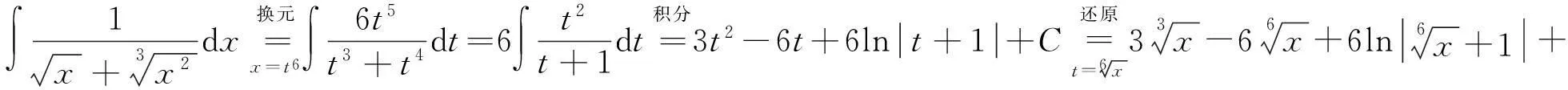
3分部积分法

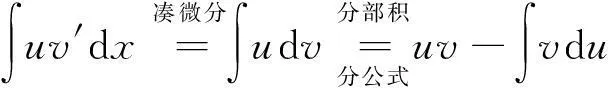
适用对象：主要适用于被积函数是两个不同类型的函数乘积的不定积分，形如∫f(x)g(x)dx.

处理方法：选取其中的一个函数u，另一个函数看成v′，通过凑微分得到dv.在使用分部积分法时，要注意两点：(1)在选取函数v′时，v要容易求出，这是分部积分法的前提；(2)积分∫vdu比∫udv简单，把一个较难的积分转化为一个较简单的积分，这是分部积分法的目的.

一般情况下u的选择顺利为“反三角、对数、幂、三角、指数”型函数，剩余的函数选为v′[5].

例4求∫xcosxdx.

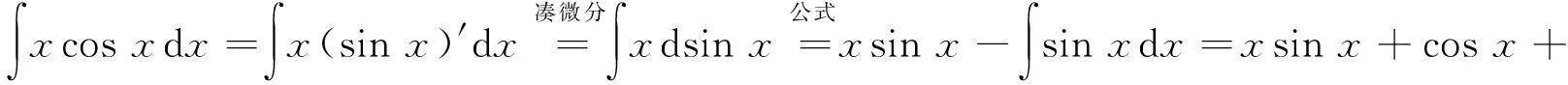
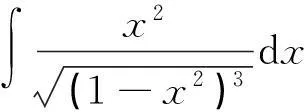
4.1多种解法

方法1第一类换元积分法.

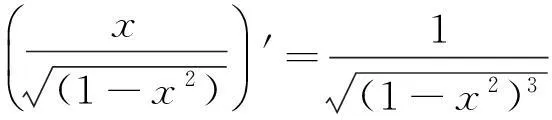
方法2第二类换元积分法.

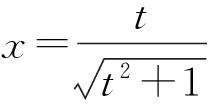
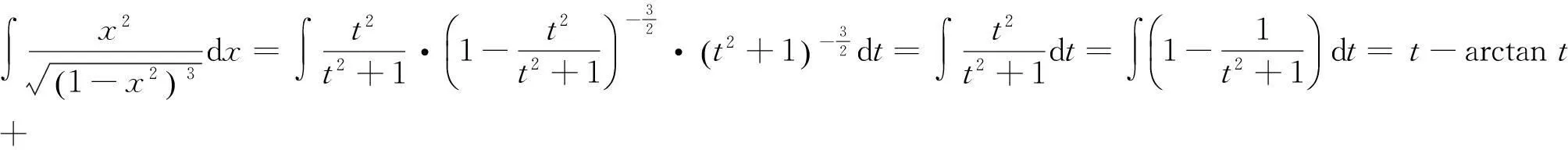
方法3第二类换元积分法.

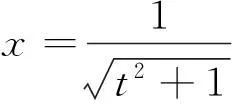
方法4第二类换元积分法.

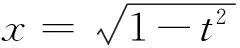
同理可得，当x<0时此结果也成立.

方法5[6]第二类换元积分法.

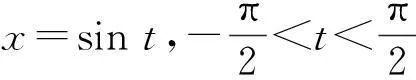
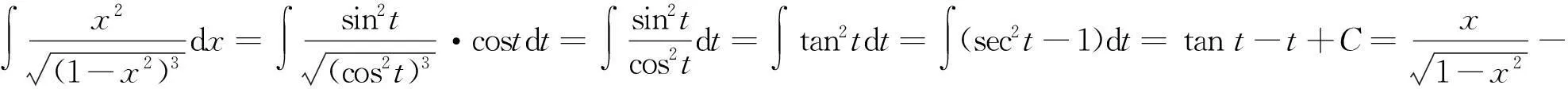
方法6先整理再换元.

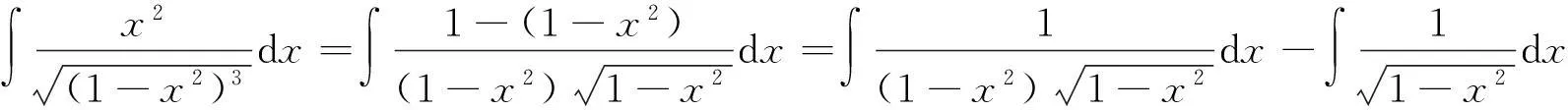
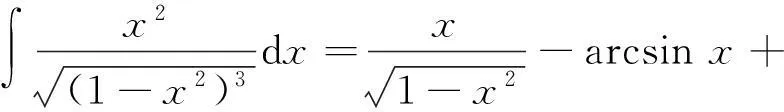
方法7[1]分部积分法.

4.2积分结果的统一

在上述第二类换元积分法中，由于用了不同的函数进行换元，故所得不定积分的结果在形式上出现了不同，下面证明上述求法的结果本质上是一样的，因此，只需证明

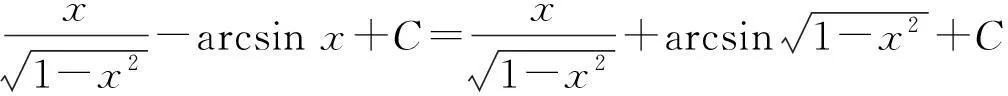
(1)

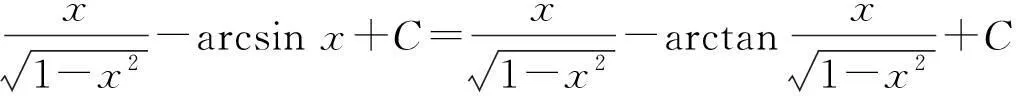
(2)

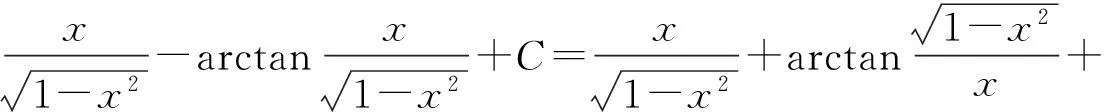
(3)

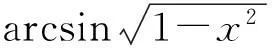
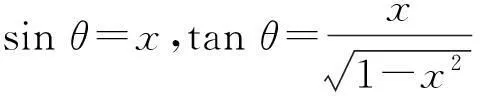
由于不定积分结果在形式上的多样性，故不同的积分方法求得的结果也不一样，它们都可能是正确的，我们只需将所求结果求导看它是否等于被积函数即可.

参考文献

[1]吴杰，胡农.高等数学:上册[M].2版.北京：高等教育出版社，2011：143-145.

[2]刘玉琏，傅沛仁.数学分析讲义：上册[M].3版.北京：高等教育出版社，2001:281-295.

[3]何挺.不定积分三种基本解题方法的归类[J].安顺师范高等专科学校学报，2004，6(4):78-81.

[4]李火生.不定积分方法的比较分析[J].闽江职业大学学报，1999(3):63-64.

[5]上宏昌.关于不定积分的分部积分法运算技巧[J].廊坊师范学院学报(自然科学版)，2014，14(4)：19-22.

[6]同济大学数学系. 高等数学:上册[M].6版.北京：高等教育出版社，2007：200-203.

Discussing the Solving Methods of Indefinite Integration

HAN Yanna

(School of Computer Engineering， Shangqiu University， Shangqiu 476000， China)

Abstract:Discussing the solving methods of indefinite integration with direct integration, substitution and integration by parts to help students master the method of indefinite integral. It can help students use these methods flexibly by solving one sample of indefinite integration with different methods.

Key words:indefinite integral； direct integration； integral method by substitution； integration by parts

收稿日期：2016-01-30

基金项目：河南省高等学校重点基金项目(16A110015)

作者简介：韩艳娜(1981—)，女，河南周口人，商丘学院计算机工程学院讲师.

doi：10.3969/j.issn.1007-0834.2016.02.014

中图分类号：O172.2

文献标志码：A

文章编号：1007-0834(2016)02-0059-04