基于优化DHGF校园信息系统评价模型应用研究

陈　震

(福州外语外贸学院，福建福州 350202)



基于优化DHGF校园信息系统评价模型应用研究

陈震

(福州外语外贸学院，福建福州 350202)

[摘要]本文深入分析校园信息系统的实施运行情况，建立综合评价体系。同时介绍基于优化权重的DHGF算法，并将其应用于实例中，实践证明该算法具有科学性和可行性。

[关键词]信息系统；DHGF；信息熵；评价模型

信息系统开发是一项浩大的工程，其可行性研究与综合评价的重要性是毋庸置疑的.信息系统拥有抽象性、创造性和绩效等特点，使得其评价因素具有灰色、模糊、难以量化的特性，造成综合评价工作异常复杂.在评价工作方面，目前国内外出现的许多评价方法都表现出各自的优点和缺点，但同时也表现出无法满足评价效率和评价质量的现象[1].为此,笔者综合不同方法的优点，优化前人评价指标不完整性，弱化权重主观性[2-3]，采用基于DHGF算法对评价指标因子权重进行组合修订，形成优化DHGF算法，并用在高校校园网信息系统评价中，实现为信息系统评价作出客观而准确的评价.

1基于改进DHGF算法的综合评价模型

1.1传统DHGF算法的介绍

DHGF算法是在灰色理论和模糊数学的基础上提出来的一种实现定性到定量转换的综合集成算法[4],由德尔斐法(Delphi)、层次分析法(Analytic Hierarchy Progress)、灰色关联(Gray Interconnect)、模糊评判(Fuzzy Evaluating) 组合运用，实现了从定性到定量的数学方法综合集成[5].

1.2DHGF优化算法介绍

在DHGF算法中，评价因子的权重是根据评价目标和专家自身的知识经验合理确定的，呈现主观的赋权法.但这种主观赋权法反映了决策者(或专家)的主观意向，客观性较差，在应用中存有较大的局限性，即无法弱化决策者(或专家)主观因素影响.故引入组合赋权法，将利用乘法合成的主观赋权值和客观赋权值融入到DHGF算法中，本文采用信息熵权客观赋权技术.信息熵权法是一种比较客观的方法,源于1840年香农提出的“信息熵”概念.根据各因子信息熵得出较为客观的因子权重[6-7]，它可以避免层次分析法人为打分的主观性，避免由专家主观因素导致其它信息丢失.

1.3DHGF优化模型的基本算法

1.3.1确定评价指标体系

首先按照WSR思想和专家的评议，利用改进的Delphi法，确定评价对象的指标体系.

O=[O1O2… On].

(1)

其中，n为评价指标的个数.

1.3.2确定评价指标权重

1.3.2.1建立矩阵U

采用层次分析法，构造比较判断权重矩阵，即在O上的模糊加权子集U,如图1、表1以及式2所示.

图1　递阶层次结构图

标度定义含义1同样重要两元素对某属性同样重要3稍微重要两元素对某属性,一元素比另一元素稍微重要5明显重要两元素对某属性,一元素比另一元素明显重要7强烈重要两元素对某属性,一元素比另一元素强烈重要9极端重要两元素对某属性,一元素比另一元素极端重要2,4,6,8相邻标度中值表示相邻两标度之间折中时的标度上列标度倒数反比较元素i对元素j的标度为n,反之为1/n

U=[U1U2…Un].

(2)

1.3.2.2熵值方法构造权重矩阵[8]

(a)求出各属性正规化矩阵.

(3)

其中，xij为第i方案中第j指标的值.

(4)

(b)求出因子的熵，ej表示为第j个属性的熵值.

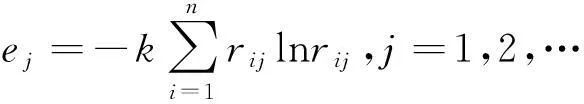
(5)

其中,k=1/lnn，n是常数时，0≤ej≤1.

(c)求出各属性权重.

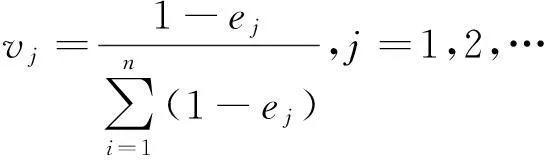
(6)

1.3.2.3计算组合权重

采用合成归一化方法进行计算：

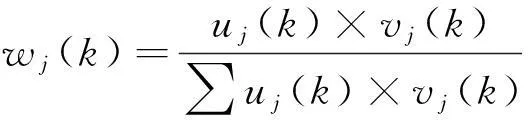
(7)

其中，wj(k)为第j个参评方案第k个评价因子的权重系数;vj为第j个参评方案第k个评价因子的客观权重值;uj(k)为第j个参评方案第k个评价因子的主观权重值.

1.3.3计算灰色权值

1.3.3.1确定评价量样本矩阵

设L=(1,2,…,i)为参加评价专家, I=(1,2,…,i)为被评价指标, 第1位评价者对评价指标i给出的评分记作d1i,则样本矩阵如式(8)所示.

(8)

1.3.3.2确定评价等级

根据WRS理论[9]，评价等级集合为 K={k1,k2,…,ke}T，灰数记为⊗.

1.3.3.3确定评估灰类

灰类要根据评价等级，通过定性分析确定，常用的白化权函数有以下三种：

(a)上限测度白化权函数如图2所示，灰类为⊗∈[d1,+∞).

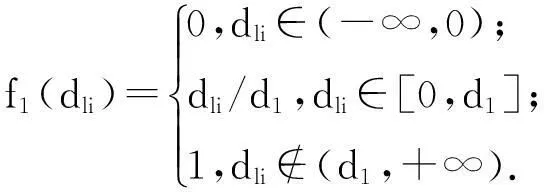
图2上限测度白化权函数

(b)适中测度白化权函数如图3所示，灰类为⊗∈[0,d1,2d1].

图3适中测度白化权函数

(c)下限测度白化权函数如图4所示，灰类为⊗∈[0,d1,2d2].

图4下限测度白化权函数

其中,d1,d2是白化权函数阀值.

1.3.3.4确定灰色统计数[10-11]

由灰类白化函数，可得dli属于第b类评估标准的权为fb(dli)，得到评价矩阵的灰色统计数，用Ljb表示评判矩阵的灰色统计数，以及用Lj表示评判矩阵的总灰色统计数，具体计算如式(9)(10)所示.

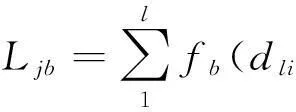
(9)

(10)

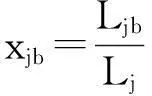
(11)

1.3.4确定模糊评判矩阵

建立评价指标的子因素模糊评判矩阵如式(12)所示.

(12)

由子因素层指标权重和模糊矩阵,可得主因素层的模糊综合评判矩阵Ai[12],如式(13)所示.

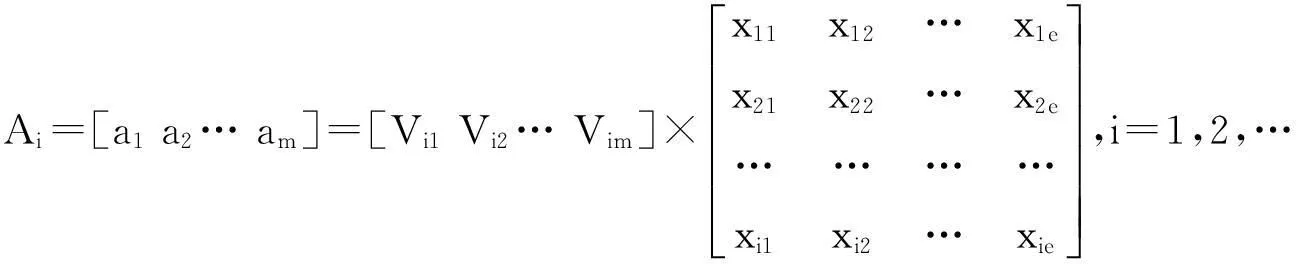
(13)

1.3.5计算评价结果

Z=A×K=Ai×[k1k2… ke]T.

(14)

由Z可以作出对方案的评价，Z值越大说明方案越好.

2实例应用

2.1确定信息系统评价体系

系统投入运行后，为了了解系统是否达到预期目的和要求，进行校园信息系统实施后的评价，评价指标体系如图5所示.

图5　评价指标体系

2.2确定评价指标权重

2.2.1层次分析法，构造比较判断权重矩阵

利用问卷形式，将专家填写的上下两两元素的相对重要性进行判断并整理成判断矩阵(图6，图7，图8).

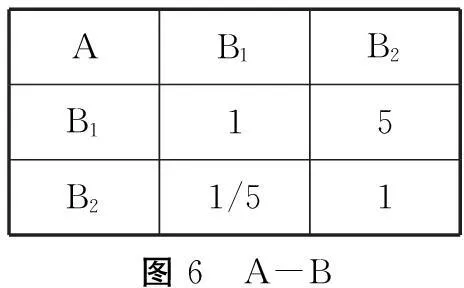
AB1B2B115B21/51图6 A-B

B1M1M2M3M1175M21/711/3M31/531图7 B1-M

B2M4M5M6M4136M51/313M61/61/31图8 B2-M

计算得出M层对A的权重Ui，并满足一致性检验的要求.

U=[U1U2U3U4U5U6]=[0.6029 0.0694 0.1610 0.1089 0.0418 0.0160].

2.2.2熵权重法

邀请6位校园信息系统方面的专家，对校园信息系统的实施运行后的情况进行打分，为了便利专家评分，规定对M[M1M2M3M4M5M6]指标统一打分，每项打分范围为1～10分。得到评分表如表2所示，根据信息熵公式，M指标的信息熵权重的结果：V=[V1V2V3V4V5V6]=[0.0464 0.5015 0.0650 0.0557 0.1920 0.1393].

表2　评分表

2.2.3组合权重

根据公式分别把Ui和Vi代入，得到W=[W1W2W3W4W5W6]=[0.3125 0.3885 0.1168 0.0677 0.0895 0.0249].

2.3计算灰色权值

2.3.1评价样本量矩阵

根据校园信息系统评价体系，采用表2的专家评分作为计算灰色权重的样本数据.

2.3.2确定评价等级

针对信息项目的特殊性及规范标准，综合专家评价等级标准，现将校园信息系统项目分为优、良、及格、差4级.

2.3.3确定评估灰类

根据评价等级，得到相应的灰数及白化权数.

第1类(优)：设灰数为⊗∈[9,+∞)，白化权函数f1(图9).

第2类(良)：设灰数为⊗∈(0,7,14]，白化权函数f2(图10).

第3类(合格)：设灰数为⊗∈(0,5,10]，白化权函数f3(图11).

第4类(差)：设灰数为⊗∈(0,3,6]，白化权函数f4(图12).

图9　白化权函数f1

图10　白化权函数f2

图11　白化权函数f3

图12　白化权函数f4

对于目标M1的各灰类的统计数为n11= f1(8)+f1(7)+f1(8)+f1(8)+f1(6)+f1(7)=4.8889;同理，n12=5.4286，n13=3.2，n14=0.根据公式n1=13.5175，同理可得出灰色评估矩阵R.

2.3.4确认模糊评判矩阵

B=W×R=[3.39163.19111.35430.0957].

2.3.5计算评价结果

Z=B×K=[3.39163.19111.35430.0957]×[9753]=8.0328,按照信息系统等级标准，可以看出该评价结果7

3结论

DHGF是集各种方法的优点而形成的一种评价方法，但在评价因子的权重考量上比较偏向主观，引进数据信息熵技术，采用组合决策权重计算方法，尽可能减避权重的主观性，得到较为客观可靠的最终权重，从而使评价结果更可信.

DHGF与信息熵的结合消除了原始数据的不同指标量纲的影响，评价结果充分利用了原始数据信息，能定量反映评价的优劣程度.且该算法对数据分布、样本量大小及评价指标的选择没有严格的限制，应用灵活、操作简便，在类似系统综合评价中有较大的应用价值，例如在文化产业综合评价的应用.

[参考文献]

[1]Gregory A.J,Jackson M.C.Evaluating methodologies:A system for use[J].Journal of Operational Research Society,1992,43(1):19-28.

[2]赵焕臣,许树柏,金生.层次分析法一种简易的新决策方法[M].北京:科学出版社,1986.

[3]董继红,李占印.DHGF集成法在高校实验室安全管理评价中的应用[J].实验室研究与探索,2013,32(9):251-254.

[4]徐维祥,张全寿.基于WSR方法论的信息系统项目评价研究[J].系统工程与电子技术,2000,22(10):4-6.

[5]徐维洋.信息系统大型工程项目评价与方法的研究[D].北京:北方交通大学,1999.

[6]郑贤斌,陈国明.基于熵技术的石化企业安全模糊综合评价方法研究[J].中国安全科学学报,2004,14(2):109-112.

[7]谢正文,孔凡玉.基于熵技术的矿山安全模糊综合评价[J].中国计量学院学报,2007,18(1):79-82.

[8]王天津,徐若倩.应用TOPSIS方法评估股票上市公司营运绩效之研究[C].企业管理研究选辑,2003:431-436.

[9]顾基发,唐锡晋.物理-事理-人理系统方法论:理论与应用[M].上海:上海科技教育出版社,2006.

[10]江金山,吴佩玲.灰色理论入门[M].台北:高立图书有限公司,1988.

[11]夏郭贤,吴汉雄.灰关联分析之线性数据前处理探讨[J].灰色系统学刊,1998(1):47-53.

[12]易德生,郭萍灰色理论与方法[M].北京:石油工业出版社,1992.

Application Research on the Evaluation Model of the Campus Information System Based on Optimization DHGF

CHEN Zhen

(Fuzhou University of International Studies and Trade ,Fuzhou Fujian 350202, China)

Abstract:This paper deeply analyzes the implementation of the campus information system, the establishment of a comprehensive evaluation system. At the same time, the DHGF algorithm based on optimization weight is introduced, and it will be applied in the case. The practice proves that the algorithm is scientific and feasible.

Key words:information system; DHGF; information entropy; evaluation model

[收稿日期]2016-02-10

[基金项目]福建省教育厅省教育厅A类科技项目“数据挖掘技术为‘海西’文化产业系统中的应用研究”(JA12365)。

[作者简介]陈震(1978- )，男，讲师，硕士，从事数据库技术、数据挖掘、人工智能研究。

[中图分类号]TP392

[文献标识码]A

[文章编号]2095-7602(2016)06-0040-06