Ambrosio-Tortorelli模型的相关改进

龚海晏，刘宏申，阮　越，刘　恒，潘　祥

(安徽工业大学计算机科学与技术学院，安徽马鞍山 243002)



Ambrosio-Tortorelli模型的相关改进

龚海晏，刘宏申，阮越，刘恒，潘祥

(安徽工业大学计算机科学与技术学院，安徽马鞍山 243002)

[摘要]Mumford-Shah(M-S)模型对于图像分割有重要的研究意义，却在实际使用中存在很大困难，故而产生了Ambrosio-Tortorelli(A-T)模型的近似方法。本文介绍了Ambrosio-Tortorelli模型泛函，以及其拐角效应在图像分割中的缺陷，针对此缺陷，改进了其几何项的椭圆逼近项，随后对本文模型进行离散化计算得到最终的分割迭代方程。通过实验可以证明本文方法的可行性。

[关键词]图像分割；Mumford-shah模型；Ambrosio-Tortorelli模型；拐角效应

1989年，Mumford和Shah提出的图像分割泛函M-S模型对于之后的能量泛函模型的研究具有重要的影响[1]，目前众多的能量分割模型是基于此模型进行研究和改进的。1997年，Chan和Vese提出的C-V模型是对原始的M-S模型进行的简化，且结合了水平集方法的基于区域的分割模型，该模型的提出在学术研究中一度成为研究的热点，得到学者们的认可[2]。Chan和Vese之所以对原始M-S模型进行简化，是由于原始M-S模型泛函的复杂性导致，对其弱形式表达的研究是完全有必要的，同时需要对弱化模型进行近似逼近的研究。1990年，Ambrosio和Tortorelli通过椭圆函数进行逼近得到A-T模型[3]，接着使用欧拉方程和有限差分法进行求解。A-T模型对于图像噪声具有很好的抑制作用，同时可以很好地得到图像的光滑和不连续点集的部分。虽然如此，该模型也存在着一些自身难以克服的缺点，如有梯度效应(gradient effect)和拐角效应(rounding effect)的问题[4]。

拐角效应是M-S模型中较明显，且为学者熟知的一个缺点。该影响主要来源于M-S模型中控制几何项的参数，随着该参数的增大，会逼迫不连续点的长度不断缩小。Mumford和Shah表示通过欧拉-拉格朗日方程的计算，几何项会产生一个控制不连续点集的曲率式。由此可见，在曲线长度的最小化会受模型分割过程中曲线曲率的影响：曲率越大，对曲线长度的缩短作用就越大，这样便会导致拐角效应，会对高曲率的曲线产生较大的影响。1997年，March和Dozio提出一个M-S的拓展模型，引进一个新的项来控制不连续点曲线的曲率[5]。虽然新增的曲率项可以减少拐角效应的影响，但是不能根本地去解决保护边缘角弱化的问题。2006年，Braides和March进一步地对M-S模型进行拓展[6]，除了长度和不连续点集的曲率项外，另增加了一个控制曲线点数目的项，这样会导致模型泛函的繁杂性，对其进行求解增加了难度。该模型的主要目的是恢复角点和不连续点曲线的连接处，这样可以避免原M-S泛函的几何项对不连续点集的影响。

本文针对A-T模型中拐角效应的影响进行改进。首先提出了模型对角点区域弱演化概念，从而降低模型对高曲率处的影响，同时能够对其进行不错的分割；另对A-T模型中几何项的椭圆式进行改进，在保证椭圆逼近的同时，能够改善好曲率对角点处的影响。对椭圆式的修改主要是在欧拉-拉格朗日计算过程中避免产生曲率式。

1Ambrosio-Tortorelli模型

Ambrosio-Tortorelli模型是对Mumford-Shah模型的近似逼近。Mumford-Shah泛函是众多著名的分割模型中比较著名的一个，它是由David Muford和Jayant Shah在1989年提出的。通过该泛函式可以将图像分割的问题转换为泛函极值的问题，然后通过数学工具方法对该模型进行最小化求解。

(1)

其中，C表示图像g中不连续的点集，即图像的边界，C将图像分割成许多的同质区域，u为除了C之外的分段光滑的图像。H1表示不连续点集的一维Haudorff度量，即图像边界的长度。参数α和参数λ为权值。M-S泛函就是寻找最优的(C0,u)，使得C成为真正的图像边界C0，并且满足分割图像u与输入图像g的误差最小。第一项为保真项，保证分割图像u接近输入图像g，以避免之间有较大的差距；第二项为平滑项，保证分割图像u除了不连续点外都尽量保持平滑。第一项为约束项，保证边界C长度尽可能的短；第三项为几何项，保证边界长度尽量的短。

对图像分割问题而言，C和u是未知的，且几何项的复杂性，导致M-S泛函难求其解。故需要对其进行弱化表达，在SBV空间基础上的M-S模型的弱形式：

(2)

比较式(2)与式(1)有两个不同点：一是后两项积分区域一致了；二是几何项由原来的长度项换成了H1(Su)，它是集合的1维Hausdorff距离，该项把原来长度的概念扩展到非光滑的曲线，而且上式各项在处理中的约束作用没有改变。但该模型的数值计算还是比较困难的，因为需要对未知的边缘长度项进行计算，无法由Euler-Lagrange方程获得最小化解。

Ambrosio和Tortorelli为了克服该问题，提出了使用一个辅助函数Mε(v)来逼近边缘长度项H1(Su)0,Mε(v)函数如下：

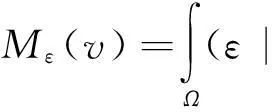
(3)

经过上述近似处理后，Mumford-Shah模型变为：

(4)

上述模型除了要求解分割图像u外，与M-S模型不同之处是不再求解不连续边缘C而是求解不连续的二维函数v了。这个v实际上就类似于图像g的边缘图像。本文称该模型为Ambrosio-Tortorelli模型，简称为A-T模型。

2Ambrosio-Tortorelli模型的改进

本文对A-T模型泛函的研究主要是针对椭圆逼近式(3)进行修改。拐角效应的现象可以从图像的像素点值的变化方面理解，角点的弱化即像素点值的变化为0→1(255)。在保留Ambrosio-Tortorelli提出的椭圆逼近项的本质Г-近似含义的情况下，对其进行稍微的改进，使其最后在角点边界处产生的像素点值不是很大，这样可以使模型很难产生拐角效应，同时在求解欧拉方程的过程中，也不会产生绝对的曲率控制项，具体如式(5)所示：

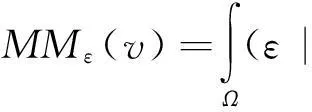
(5)

这样可以得到新的A-T模型：

(6)

然后，计算(6)的欧拉方程：

(7)

最后，使用与A-T模型同样的离散化方法对(7)进行离散。这样便得到了改进模型的迭代演化方程：

(8)

其中，

(9)

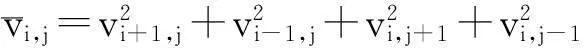
(10)

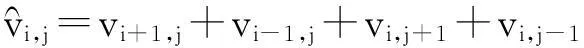
(11)

|.

(12)

以上对A-T模型的改进虽然只是针对了几何项，通过实验可以发现,对A-T模型的拐角效应的缺陷的改善是比较明显的。本文模型的改进只是针对曲率较大的地方，而对于图像的其它区域是没有任何影响的，保持了原模型的分割特性。

3实验结果与分析

为了验证本文提出的模型对于原模型的缺陷是否有所改进，对如图1(a)分别使用原A-T模型、March-Dozio模型、本文提出的模型进行分割实验。实验环境为64位win7下的VS2010。当模型中参数α的值很大时，A-T模型的拐角效应才会出现，本实验参数α和其它参数值的设置如表1所示。

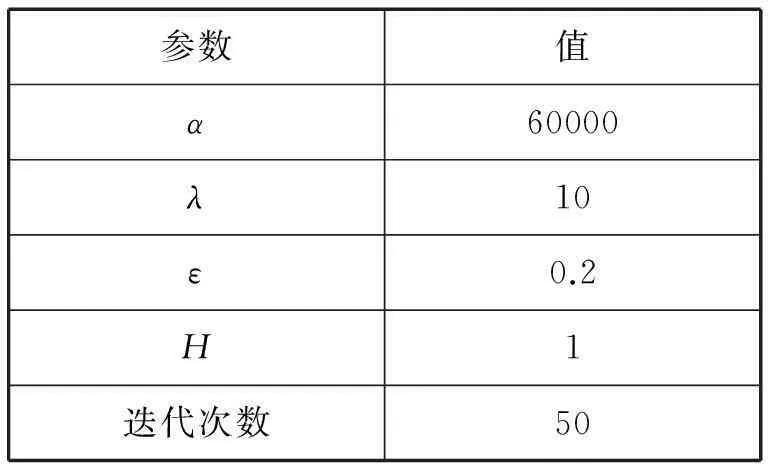
表1　A-T模型参数设置

图1(a)、(b)、(c)、(d)分别为实验256×256的实验图像、A-T模型分割图像、March-Dozio模型分割图像、本文模型分割图像。从图1(b)可以明显看出角点处的弱化现象，而March-Dozio模型虽然可以避免拐角效应的产生，但角点处还是存在些点迹，且轮廓模糊。将图1(d)与以上两个模型分割对比可以看出，在角点和边界有一定改进。

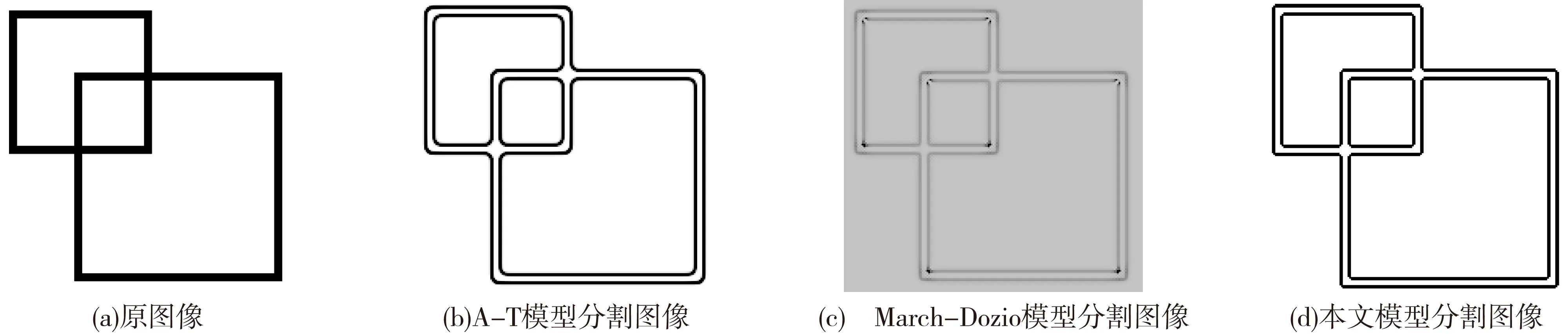
图1　模型分割实验对比

4结语

A-T模型对于图像分割有一定的研究意义，对于普通图像其分割速度和分割效果都是令人满意的。本文针对该模型的拐角效应的缺陷进行改进，主要在保证A-T模型泛函逼近M-S模型的同时，通过对模型泛函的椭圆逼近项的修改。经过实验可知，本文模型的分割图像的角点处相对于原模型有明显的进步。

[参考文献]

[1]Mumford D,Shah J.Optimal approximation by piecewise smooth functions and associated variational problems [J].Communication on Pure and Applied. Mathmatics,1989,42(9):577-685.

[2]Chan T,Vese L.Active contour without edges[J].IEEE Transactions on Image Processing,2001,10(2):266-277.

[3]Ambrosio,L,Tortorelli,V.Approximation of functionals depending on jumps by elliptic functionals via C-convergence[J].Communications on Pure and Applied Mathematics,1990,43(8):999-1036.

[4]Alfonso Vitti.The Mumford-Shah variational model for image segmentation: An overview of the theory,implementation and use[J].ISPRS Journal of Photogrammetry and Remote Sensing,2012(69):50-69.

[5]March R,Dozio M.A variational method for the recovery of smooth boundaries[J].Image & Vision Computing,1997, 15(9):705-712.

[6]Braides,A.March,R.Approximation by C-convergence of a curvature depending functional in visual reconstruction[J].Communications on Pure and Applied Mathematics,2006,59(1):71-121.

[7]Ambrosio,L,Tortorelli,V.Approximation of functionals depending on jumps by elliptic functionals via C-convergence[J].Communications on Pure and Applied Mathematics,1990,43(8):999-1036.

[8]Ambrosio,L,Tortorelli,V.On the approximation of free discontinuity problems[J].Bollettino dell Unione Matematica Italiana,1992(B6):105-123.

[9]Alfonso Vitti.The Mumford-Shah variational model for image segmentation:An overview of the theory,implementation and use[J].ISPRS Journal of Photogrammetry and Remote Sensing,2012(69):50-69.

Ambrosio-Tortorelli Model Improvement of the Model

GONG Hai-yan, LIU Hong-shen, RUAN Yue, LIU Heng, PAN Xiang

(School of Computer Science and Technology, Anhui University of Technology, Ma’anshan Anhui 243002, China)

Abstract:Mumford-Shah(M-S) model for image segmentation has important research significance, but there is a big difficulty in the practical use, thus Ambrosio - Tortorelli model and the effect of the corner of the defects in the image segmentation have been introduced in this paper, aiming at the defects, we improve its geometric ellipse approximation of the item.Then discretization model in this paper calculates the final segmentation iterative equation.Through the experiment proves this method is feasible.

Key words:image segmentation; Mumford-shah model; Ambrosio-Tortorelli model; rounding effect

[收稿日期]2016-03-08

[基金项目]国家自然科学基金资助项目“不可靠无线传感器网络中自适应稀疏压缩采样关键技术研究”(61402009)。

[作者简介]龚海晏(1990- )，男，硕士研究生，从事图像处理研究。

[中图分类号]TP391

[文献标识码]A

[文章编号]2095-7602(2016)06-0050-04