活跃在高考中的高斯函数

王　勇　芮华云

(湖北省襄阳市第一中学,441000)

活跃在高考中的高斯函数

王勇芮华云

(湖北省襄阳市第一中学,441000)

高斯函数是一个特殊且重要的函数,在数学竞赛试题中屡见不鲜,在近几年高考试题中也频频出现,涉及的问题颇具思考性和挑战性,是考查考生数学能力和数学灵气的极好素材,值得高度重视.本文介绍高斯函数的定义、常用性质和典型问题,供参考.

一、定义

设x∈R,用[x]表示不超过x的最大整数,则y=[x]称为高斯函数,也叫取整函数.显然,任一实数x都能写成整数部分与非负纯小数部分之和,即x=[x]+r(0≤r<1).

二、常用性质

根据高斯函数[x]的定义,可以得到它的一些常用性质.现介绍如下,限于篇幅,证明从略.

性质1y=[x]的定义域是R,值域是Z,其图象如图1所示.

性质2当x1≤x2时,[x1]≤[x2].

性质3若n∈Z,则[n+x]=n+[x].

性质4x-1<[x]≤x<[x]+1.

性质5对于一切实数x,y,有

[x]+[y]≤[x+y]≤[x]+[y]+1.

性质6若x≥0,y≥0,则[xy]≥[x][y],特别地,[nx]≥n[x],其中n∈N.

特别地，有[[x]]=[x].

三、典型问题

1.研究新函数的性质

例1(2013年湖北高考题)x为实数,[x]表示不超过x的最大整数,则函数f(x)=x-[x]在R上为()

(A)奇函数(B)偶函数

(C)增函数(D)周期函数

解作出函数f(x)的大致图象如图2所示,观察图象,易知函数f(x)是周期函数，故选D.

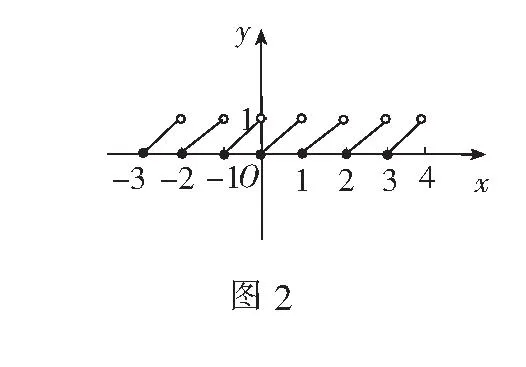
评注函数f(x)=x-[x]的定义域为R,值域为[0,1),是非奇非偶、以1为周期的非单调函数,在每个区间[n,n+1)(n∈Z)上都是单调增函数.如能熟练掌握函数f(x)={x}=x-[x]的图象和性质,则对破解相关综合性问题大有裨益.

当x∈[2,3)时,[x]=2,

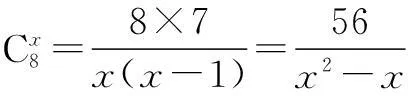
2.探求函数的解析式

例3(2010年陕西高考题)某学校要召开学生代表大会,规定各班每10人推选一名代表,当各班人数除以10的余数大于6时再增选一名代表.那么,各班可推选代表人数y与该班人数x之间的函数关系用取整函数y=[x]([x]表示不大于x的最大整数)可以表示为()

解法1直接探求.设x=10m+α(m∈N,0≤α≤9).

当0≤α≤6时,

当6<α≤9时,

结合各选项可知,本题应选B.

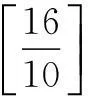
评注本题以学生比较熟悉的推选代表问题为背景,考查构建函数模型的能力,两种解法都值得充分借鉴和品味.

3.判断恒成立问题

例4(2013年陕西文科高考题)设[x]表示不大于x的最大整数,则对任意实数x,有()

(A)[-x]=-[x]

(C)[2x]=2[x]

解选取特殊值,利用排除法求解.

对于A,取x=1.5,则[-x]=[-1.5]=-2,-[x]=-[1.5]=-1,显然[-x]≠-[x].

对于C,取x=1.5,则[2x]=[3]=3,2[x]=2[1.5]=2,显然[2x]≠2[x].

由以上分析可排除A、B、C,故选D.

评注本题考查新记号[x]的现场阅读能力及特殊值法.重点考查了审读信息并接受信息的迁移能力,考查了推理论证能力和数据处理能力；对选择题的特殊解法(特值验证并结合排除法)考查得也相当充分.

例5(2013年陕西高考题)设[x]表示不大于x的最大整数,则对任意实数x,y,有()

(A)[-x]=-[x]

(B)[2x]=2[x]

(C)[x+y]≤[x]+[y]

(D)[x-y]≤[x]-[y]

解法1由高斯函数的性质7，排除A;由性质6，排除B;由性质5，排除C.故选D.

评注熟悉高斯函数的性质,求解起来轻松自如,实为“秒杀”.

解法2结合特殊值,利用排除法求解.

对于A,取x=1.5,则[-x]=[-1.5]=-2,-[x]=-[1.5]=-1,显然[-x]≠-[x];

对于B,取x=1.5,则[2x]=[3]=3,2[x]=2[1.5]=2,显然[2x]≠2[x];

对于C,取x=y=1.6,则[x+y]=[3.2]=3,[x]+[y]=[1.6]+[1.6]=2,显然[x+y]>[x]+[y].

由以上分析可排除A、B、C,故选D.

评注鉴于众多考生并未系统学习高斯函数,命题者的初衷就是考查考生的信息迁移能力和选择题的特殊解法(特值验证并结合排除法).

4.与数列交汇融合

(A)是等差数列但不是等比数列

(B)是等比数列但不是等差数列

(C)既是等差数列又是等比数列

(D)既不是等差数列也不是等比数列

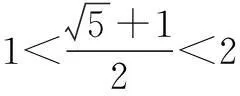
评注本题比较简单,直接考查考生对高斯函数定义的理解,高斯函数与数列的交汇是本题的“亮点”所在.

5.与方程及不等式的巧妙结合

例7(2015年湖北高考题)设x∈R,[x]表示不超过x的最大整数.若存在实数t,使得[t]=1,[t2]=2,…,[tn]=n同时成立,则正整数n的最大值是()

(A)3(B)4(C)5(D)6

解若n=3, 则

若n=4,则

若n=5,则

(*)

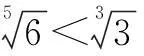
综上所述，所求正整数n的最大值为4. 故选B.

评注本题考查考生对新符号[x]的领悟程度及不等式组的解法；考查考生的阅读理解能力、抽象概括能力、运算求解能力、数据处理能力等.

通过本文可以看出,活跃在高考中的高斯函数,虽其外表简单朴素,但其内涵深邃,在解题中常需要结合分类讨论、数形结合、转化与化归等数学思想方可顺利达到目的.