例谈多变量问题的减元策略

雷亚庆

(江苏省南京市大厂高级中学，210044)

例谈多变量问题的减元策略

雷亚庆

(江苏省南京市大厂高级中学，210044)

含有多个参数的目标函数的最值问题近几年在高考中经常出现,而且难度较大,学生对此类问题感觉比较棘手．解决多元目标函数的关键是通过减元把它变为单变量的函数问题或者双变量的基本不等式问题．如何减元,具有较强的技巧性,常常需要根据题目的特点,灵活选择合适的消元方法．

一、直接法

所谓直接法,就是直接利用所给的几个变量间的等量关系式，用其他变量表示其中一个变量，从而达到减元的目的．

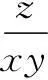
解由已知得z=x2-3xy+4y2.

又∵x,y>0，

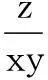
∴x+2y-z=-2y2+4y

=-2(y-1)2+2(y>0)

∴当y=1,x=2时,x+2y-z有最大值2，选C.

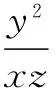
解由x-2y+3z=0，得

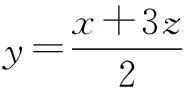
当且仅当x=3z时取“=”.

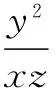
二、换元法

解多元目标函数问题时,可以把含有两个变量的某个式子看成一个整体,用一个新的变量去代替它,从而使问题得到简化,这叫换元法．换元的实质是转化,关键是构造元和设元,理论依据是等量代换,目的是变换研究对象,将问题移至新对象的知识背景中去研究,从而使问题简单化,变得容易处理．

例4已知a>b>c,求证：

解设a-b=x,b-c=y，则

a-c=x+y.

因为a>b>c，所以x>0,y>0.

问题转化为：已知x>0,y>0,求证：

结论显然成立.

三、利用除法

有些多元问题,所给已知条件和目标都是含有多参数的齐次式,这种情况下利用等式或分式的基本性质在等式或不等式两边或分式的分子和分母同除以其中一个变量然后换元就可以巧妙的起到减元的效果.

由b+c≥a且a,b,c均为正数，得

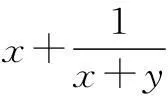
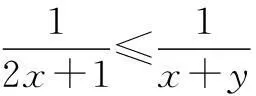
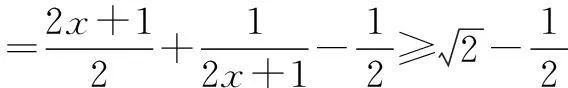
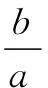
分析由题意，得

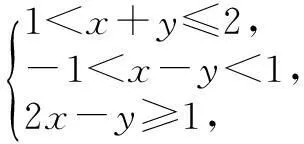
四、降位法

所谓降位法,就是在处理多元问题时将其中一个变量的地位“降低”,让它作为字母系数,这样问题就有多元问题转化为二元或一元的大家非常熟悉的方程或不等式的问题,从而顺利解决．

例8(2014年浙江高考题)已知实数a,b,c满足a+b+c=0,a2+b2+c2=1,求a的最大值.

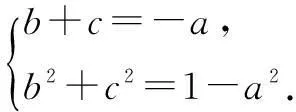
设b=x,c=y，则问题转化为若方程组

有解，求a的取值范围中的最大值.

于是问题归结为：当直线x+y=-a与圆x2+y2=1-a2有交点(相交或相切)时(如图1),求a的取值范围.

评注该题涉及到三个变量,用代数法处理有些棘手.我们首先设b=x,c=y,把a的地位由变量降为参系数,这样问题就转化为含参数的二元方程组有解的问题,进一步转化为直线与圆的位置关系问题,利用几何法较容易的得到问题的解．

减元思想是中学数学的重要思想方法之一.它既可以显性的表现为具体的技能,如降幂、减少变量的个数等,又指导着思维的方向,如对题设或结论的简化意识等．在解题的动态思维过程中,如能紧扣消元的数学思想,重视消元法的应用,就会感受柳暗花明又一村的乐趣.