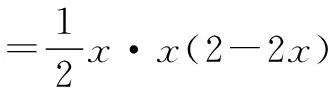构造基本不等式求函数最值的八种策略

施贵军

(贵州省息烽县第一中学，551100)

构造基本不等式求函数最值的八种策略

施贵军

(贵州省息烽县第一中学，551100)

(1)表达式中含变量的项均为正;(2)表达式中含变量的项之和或积为定值;(3)表达式中含变量的项可以相等，简称“一正,二定,三相等”.搞清楚了这几点,在运用基本不等式求解相关最值问题时就会少犯错误.下面谈一谈运用基本不等式求最值的解题策略.

策略1负化正构造

如果含变量的项是负数,可通过添加负号,将变量转化为正数,再利用基本不等式求解.

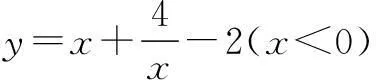
解因为x<0,所以-x>0,则

策略2常数代换构造

在求二元或三元条件最值时,若能观察到已知条件中的“1”(或可化为“1”)与要求解的式子的关系(常数通常可变为1)，并能灵活地进行代换,则可快速求解.

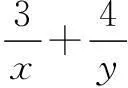
解因为x+y+z=2,所以

策略3添项构造

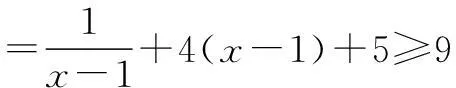
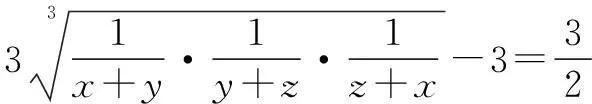
策略4拆项构造

除了添项构造,有时为了创造应用基本不等式的条件,需要将一些项作适当的变形,拆分成多项之和或分解为多个因子之积,使得和或积为常数.通常情况下,为了使等号成立,遵循“平均拆分”原则.

例6已知ab>0,且ab2=2,求ab+b2+3的最小值.

当且仅当a=2,b=1时取等号,所以ab+b2+3的最小值是6.

例7已知0

分析这是一个求三次函数在开区间(0,1)上的最值问题,一般用导数解决,通过观察构造基本不等式求解方法更好,速度更快.

解因为0

策略5配凑构造

用基本不等式求最值时,根据所求式的结构特点,常通过配凑方法把所求式的某些因子同乘以或同除以某一正数,使含变量的各因子之和(积)为定值且能够相等.

策略6平方构造

解题中常会遇到带有二次根号的函数最值求解,若观察到被开方数和为定值,则可采用平方凑和为定值解决.

分析本题解法较多,可转化为二次函数或用导数求解,也可用基本不等式求解.

策略7换元构造

对于结构比较复杂的式子,通过变形可以整体上换元构造基本不等式求解,此法多用于多元函数最值的求解.

分析这是一个二元最值问题,且题设中没有给出x,y的关系,经过适当变形可用基本不等式求解.有三种变形途径:(1)分子分母同时除以xy;(2)分子分母同时除以x2;(3)分子分母同时除以y2.采用第三种途径更好.

策略8引入参数构造

参数具有桥梁的作用,引入参数是为了把问题转化为对参数的讨论.如果上述几种策略无法或不容易构造基本不等式,则可考虑引入参数.

例11求函数y=x(x+3)(5-x)(0

分析和例7一样,这是一个三次函数求最值问题,通常用导数求解,能否构造基本不等式解决呢?例7中我们构造了x+x+(2-2x)=2(常数),但本例中x+x+3+5-x不是常数,而且不易观察出如何配凑系数,若要构造基本不等式求解,可用待定系数法调整系数.

解设aby=ax·(x+3)·b(5-x)(其中a>0,b>0,a,b为待定系数).

又设ax+(x+3)+b(5-x)=(a+1-b)x+(3+5b)为常数,则

a-b+1=0.

①

又由取等号的条件ax=x+3=b(5-x)，得

②

由①，②，解得

当且仅当2x=x+3=3(5-x),即x=3时取等号，故函数最大值为36.

实际上，对于这种类型的三次函数最值问题,只要能够保证通过配凑系数使各项之和为定值且能够取等号,均可利用基本不等式求解，无需采用导数.

总之,在使用基本不等式求函数最值时一定要注意基本不等式成立的条件(一“正”,二“定”,三“相等”)；一定要多思考,多尝试,多研究，这样才会有更深入的认识.