利用参数t的几何意义巧解距离问题
2016-07-07董海涛
董海涛
(安徽省阜阳市第三中学,236000)
利用参数t的几何意义巧解距离问题
董海涛
(安徽省阜阳市第三中学,236000)


其中参数t的几何意义是:|t|表示直线上的动点M(x,y)到定点M0(x0,y0)的距离,若t>0,则动点M在定点M0的上方;若t<0,则动点M在定点M0的下方;若t=0,则动点M与定点M0重合.
下面结合具体实例,体会利用直线参数方程中参数t的几何意义,简洁快速地求解与距离有关的问题.
例1已知过点M(-1,2)且斜率为-1的直线l与抛物线y=x2交于A,B两点.(1) 求|MA||MB|的值;(2) 求|AB|的值.
解直线的参数方程为

|MA||MB|=|t1||t2|=2,
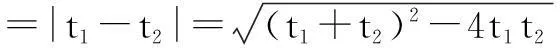

评注如果按照常规方法联立直线与抛物线方程,求出交点A,B的坐标,再求线段AB的长和点M到A,B两点距离之积,显然运算量较大,而利用直线参数方程中参数t的几何意义,问题的求解则变得十分简洁.
变式1已知过点M(-1,2)且斜率为2
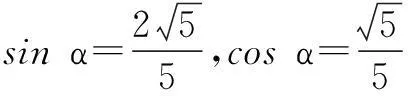
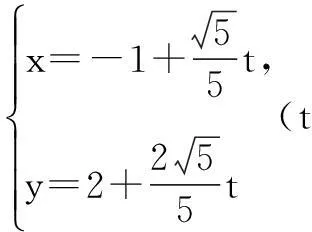
|MA||MB|=|t1||t2|=5,
|AB|=|t1-t2|
=10.
变式2已知直线l的参数方程为

点M(-1,2),直线l与抛物线y=x2交于A,B两点.(1) 求|MA||MB|的值;(2) 求|AB|的值.
解把直线的参数方程
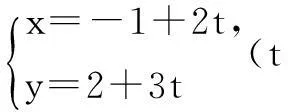
改写为“标准形式”
(其中m为参数).
代入抛物线方程,得

根据韦达定理,得

由参数m的几何意义,得
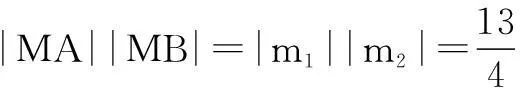
|AB|=|m1-m2|

评注把直线参数方程的非标准形式化为标准形式很关键,这样才能体现参数t的几何意义.
变式3已知过点M(-1,2)且斜率为-1的直线l与抛物线y=x2交于A,B两点,C为线段AB的中点,求|MC|的值.

变式4已知过点M(-1,2)且斜率为-1的直线l与抛物线y=x2交于A,B两点,C在线段AB上,且|AC|=2|CB|,求|MC|的值.
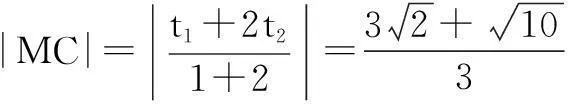
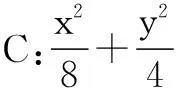


根据参数t的几何意义,可知
|AB|=|t1-t2|

根据AB⊥DE,可得



例3长度为l(l>4)的线段AB的两端在抛物线y2=4x上移动,(1)求线段AB的中点M的轨迹方程,(2)求线段AB的中点M到y轴的距离的最小值.
解(1)设M(x0,y0),则直线AB的参数方程为



①
因为线段AB的长度为l(l>4),即
l=|t1-t2|,
所以l2=(t1+t2)2-4t1t2
②
(4x-y2)(4+y2)=l2.
(2)由(1)知


评注本题中点M虽然不是定点,但由参数t的几何意义以及“线段AB的中点M”仍然可知t1+t2=0,这是本题解决的关键所在.掌握参数t的几何意义的本质,辅以根与系数的关系,为我们的解题带来了耳目一新的感觉,提供了无穷的思维想象空间和广阔的解题思路,这是传统的解法无法比拟的.
熟练运用参数t的几何意义解与距离有关的问题,可以减少运算,提高解题速度,并且可以将解出的代数结果进行几何解释,体现了数形结合的思想.
