姊妹花开形相似 貌合神离质异同

张爱华　束荣盛

(江苏省扬州大学附属中学，225002)

姊妹花开形相似貌合神离质异同

张爱华束荣盛

(江苏省扬州大学附属中学，225002)

在平时的教学过程中,常常会遇到许多貌合神离的题型和问题,条件很相似,却又存在着本质的差异.若对题目审视不到位,就极易混淆,从而得出错误的结论,具有这样特点的题目我们可称其为“姊妹题”.下面以几对 “姊妹题”为例,分析其解题思路、探究其本质.

一、形似质同,多题归一

分析两题都是三角函数求值,一般解题思路是:先进行角的变换.

(1)中角的变换的思维链如下：

已知角

(2)中角的变换的思维链如下：

已知角

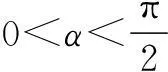
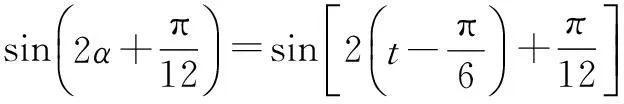
二、形似质异,找出差异

例2(1)若函数f(x)=x2+kx-3是[1,+∞)上的单调递增函数,则实数k的取值范围是______;

(2)设bn=n2+kn-3,若{bn}是单调递增数列,则实数k的取值范围是______.

三、形异质同,揭示本质

例3(1)(2004年全国高考题)由动点P向圆x2+y2=1引两条切线PA、PB,切点分别为A、B,∠APB=60°,则动点P的轨迹方程为______;

(2)(2007年湖北高考题)由直线y=x+1上的一点向圆(x-3)2+y2=1引切线,则切线长的最小值为()

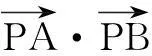
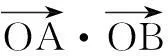
分析这类问题形式不同,但背景相近,解题方法均可化为图1中相关几何元素.

如图1,PA,PB是圆O的切线,A,B是切点,则有如下相关结论:

(1)OA⊥PA,OB⊥PB;

(2)P,A,O,B四点共圆;

(3)S四边形PAOB=2S三角形PAO

=r2cos 2∠POA

=r2(2cos2∠POA-1)

=PA2cos∠APB

=PA2cos 2∠APO

=PA2(2cos2∠APO-1)

评注(1)以上问题均可转化为求OP的值或最值来思考.

(2)将问题背景相近、解题方法或思考问题角度相同的题型放在一起进行研究,有利于揭示数学问题的本质,提升学生剖析问题的能力.在平时教学中应始终围绕一道或一些优秀的高考试题引领学生进行分析、思考、探究,可以激起学生的求知欲望与创新热情,使课堂教学达到高效,充分发挥这些高考试题的教育功能.

四、教学感悟

常言道,人生有三重境界:看山是山,看水是水;看山不是山,看水不是水;看山还是山,看水还是水.经历否定之否定后再生的“山”和“水”,就是鲜活的“山”和“水”.类似地,同一个数学概念、公式、定理、法则的表现形式可以多种多样.学习者常因缺乏相关的知识经验、认知水平较低,不能看清它的本质属性,被其表面形式所迷惑,导致理解偏差.因此我们在研究概念、公式、定理、法则的时候,往往要经历这否定之否定的再生历程,才能领悟其中蕴含的鲜活思想.

英国哲学家罗素曾经指出:“凡是你教的东西,要教得透彻.”为求“透彻”,教师必须钻研教材,理清知识发生的本源,把握教材中最主要、最本质的东西,引领学生到达“看山还是山,看水还是水”的学习境界.在平时学习中,将这些 “姊妹题”进行类比处理,在加深题目的理解、题目的挖掘、审题能力的培养等方面,都是大有好处的.

的直线l与抛物线y=x2交于A,B两点.(1) 求|MA||MB|的值；(2) 求|AB|的值.